基于加权距离的机械振动多源信号盲分离

关正伟，黄 娜，党晓圆，邢阳阳

(重庆邮电大学移通学院，重庆 401520)

1 引言

随着工业行业的不断发展，盲源信号分离技术在通信、机械、语言处理等领域中具有非常重要的应用价值[1]。机械振动信号通常情况下是由多个源信号所构成。但实际应用中，机器之间并不是孤立存在的，多个机器可形成机械系统，能够同时进行工作。机械振动源有很多，且机械振动信号传播途径较为复杂，导致环境噪声很大，给机械振动信号识别与分离过程造成了较大困难。传统方法多数采用线性瞬时混合模型，只可使用单一线性滤波器对振动信号进行处理。因此，从混合信号中获取独立的振动信号源，并将其进行准确分离，对机械状态识别及机械故障诊断有着至关重要的意义[2-3]。

高敬贝[4]等人提出基于时频分析的多源信号分离方法，该方法首先对机械局部振动脉冲波形序列进行记录，对其进行时频分析，获取典型的机械局部振动脉冲的时间-频率-幅值等特征；然后将其特征与构建典型局部振动模型的时频数据库进行混合，利用时频相似度与仿射聚类方法对记录的振动脉冲群进行分析且分类，最终实现机械多局部振动信号的分离。但该方法在对机械振动多源信号进行分离时，没有通过加权距离对振动信号进行去噪，难以避免噪声对被测振动信号的干扰，导致分离信号的信噪比较低。程浩[5]等人提出基于双AR模型的多源信号分离方法，该方法针对机械振动信号处于高频阶段的信号独立性，分别构建不同阶次的自回归(AR)模型，需对AR模型阶数和参数进行估计。首先，采用自适应原子分裂算法对回波谱进行稀疏估计，取得一阶与二阶的混合特征以及由该特征构成的自相关函数的系数；其次，以该特征为依据，构建两个自回归模型，对模型的自相关函数的系数分别进行计算，将获取的自相关函数的系数逐一进行对比，当全部的自相关系数都很近似相等时，则实现对机械振动多源信号的分离。但该方法在对机械振动多源信号进行分离时，难以控制噪声污染以及无法保留信号细节，导致分离速率较低。陈一飞[6]等人提出基于奇异值阈值和DSS的多源信号分离方法，该方法首先采用SURESVT算法将DSS算法中的奇异值分解过程进行替换，对观测数据所对应的奇异值进行计算，获取最优阈值；其次，对观测数据的奇异值进行紧缩操作，达到提高信噪比的目的，完成对观测数据的白化处理，最终对白化后的信号数据进行分离。但该方法在对机械振动多源信号进行分离时，未有效去除背景噪声，没有呈现较好的振动信号分离性，导致误分率较高。

为了解决传统方法存在的问题，本研究提出了基于加权距离的机械振动多源信号盲分离方法，该方法首先利用加权距离对机械振动信号进行去噪，其次结合Gabor变换实现对机械振动信号的盲分离。

2 基于加权距离的噪声信号估计

由于机械振动信号通常处于高频阶段，为了有效地对非稳定时变噪声进行估计，采用距离加权对机械噪声信号进行处理[7]，具体流程如图1所示。

图1 基于加权距离谱减的清音分离原理图

当机械背景噪声处于时变的非平稳噪声时，此时每帧信号长度为20ms，当某个清音块出现时延情况时，此时的清音单元之间所含有的残余噪声会出现一定差异。传统算法在对噪声进行估计时，一般将相邻浊音块之间时频单元标记为0。若此时的时频单元与清音单元的距离间隔较远，证明此时的时频单元所含有的噪声能量不符合清音单元[8]。

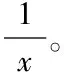
对清音块中的某个时频单元进行定义，即ucm，对该时频单元内存在的噪声能量，定义为′(c，m)，其计算公式如下

(1)

式中，时频单元uci所含有的能量表示为E(c，i)；时频单元uci的初始掩码标记表示为y(c，i)；清音块的开始与结束时间帧分别表示为m1和m2；清音块的前一个浊音块所对应的时间帧表示为l1；与该清音块相邻的后一浊音块所对应的时间帧表示为l2。

由式(1)可知，清音块中所含有的时频单元，每个时频单元所对应的估计噪声能量均不相同，时频单元内的干扰噪声能量会随着每个相邻的噪声点中的能量变化而变化。若出现某一个噪声单元距离清音单元较为接近，此时的单元之间所含有的噪声能量也是十分接近的，在对时频单元所包含的噪声能量进行估计后，对清音单元进行谱减[9]。

假设时频单元ucm中所含有的语谱能量表示为X(c，m)，属于清音块中的时频单元ucm所估计出的残余噪声能量表示为′(c，m)，该时频单元的局部信噪比表达式如下

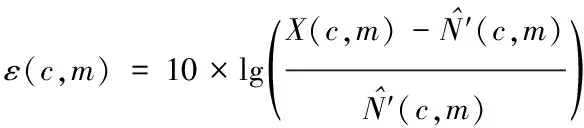
(2)

式中，时频单元ucm的局部信噪比表示为ε(c，m)；时频单元ucm所含有的语谱能量表示为X(c，m)；时频单元ucm中所含有的干扰噪声能量表示为′(c，m)。

3 基于Gabor变换的机械振动信号盲分离方法

采用Gabor变换对机械振动信号进行时频滤波，对时频平面进行定义，表示为(t，f)，将时频平面进行转换，形成两个离散采样网格参数为k和l的平面，处于二维平面(k，l)上表征非平稳信号。

信号s(t)的Gabor展开定义为

(3)

式中，时域中的抽样点数表示为∞；Gabor变换系数表示为dk，l；周期延伸的基本函数表示为gk，l(t)；两个二维平面的采样网格参数分别表示为k、l。

式(3)中的Gabor变换系数dk，l可通过RDGT获取，即

(4)

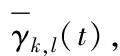
多源信号盲分离的主要原理是当源信号与传输通道参数未知的情况下，将源信号的统计特征进行输入，利用观测信号将源信号进行分离的过程[10]。

假设有n个独立的信号源，将其表示为S=s1，s2，s3，…，sn，此时信号源经过的m个传感器所输出的信号表示为X=x1，x2，x3，…，xm，将不同信号传输到传感器的时间假设是瞬时的，可以忽略不计，则瞬时线性混合模型表示为：

X=AS

(5)

式中，X表示为混合信号，S表示为源信号，A表示为混合矩阵。

对式(5)两端同时进行Gabor变换，得到下式

(6)

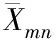
当时频平面中的某一区域在Gabor变换时，只有混合信号的存在，其中，k1⊂k、l1⊂l，此时该区域中混合信号经过Gabor变换后，取得任意分量可表示为

(7)

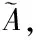
(8)

若全部源信号均由正弦信号所构成，则该方法更加便于实现振动信号的分离，对式(1)中S(t)的第h个分离进行假设，定义为

(9)

式中，源信号sh(t)中的各个分量所对应的频率表示为whr，且频率是不相等的，源信号sh(t)是由rh个不同频率的分量所组成的，各个频率分量所处于源信号中的系数表示为bhr。此时，混合信号的第i个分量计算公式如下

(10)

式中，源信号的总数表示为n，混合矩阵A中第i行第h列的元素表示为aih。

对式(10)进行Gabor变换，且采用Gabor变换的双正交条件，得到下式

(11)

混合信号中的其它分量xj(t)与xi(t)的Gabor展开系数的比值表示为

(12)

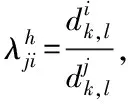
(13)

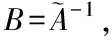
(14)

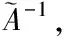
4 实验与结果

为验证上述设计的基于加权距离的机械振动多源信号盲分离方法的有效性，设计如下仿真。

选取一台工作效率为0.95的机械作为实验设备，实验环境如下：排气压力0.01Mpa，温度120℃，进汽蒸汽热焓H=2939.9kJ/kg，排汽蒸汽热H=2706.35kJ/kg，螺杆动力机内效率为0.65。采集该机械设备的振动信号，并对该机械设备振动信号实施盲分离。

为增强实验结果的对比性，分别采用基于加权距离的机械振动多源信号盲分离方法(方法1)、基于时频分析的多源信号分离方法(方法2)、基于双AR模型的多源信号分离方法(方法3)进行相关实验。

首先以分离结果信噪比作为评价分离效果的指标，将3种不同方法分离结果的信噪比进行对比，结果如表1所示。

分析表1数据可知，方法1的分离结果信噪比要高于方法2和方法3，可证明方法1的分离效果更好。这是因为方法1在对机械振动多源信号进行分离过程中，通过加权距离对机械振动信号进行去噪处理，有效去除噪声对被测振动信号的干扰，提高了分离信号的信噪比，取得了较好的分离结果。

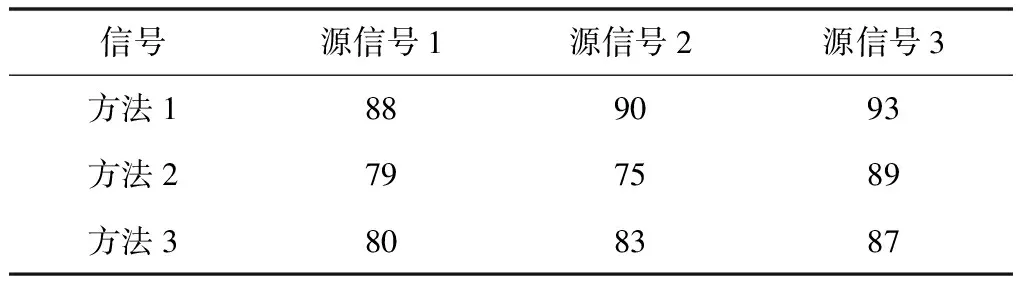
表1 不同方法分离信号的信噪比对比结果(dB)

接下来对比不同方法的分离速率，对比结果如图2所示。

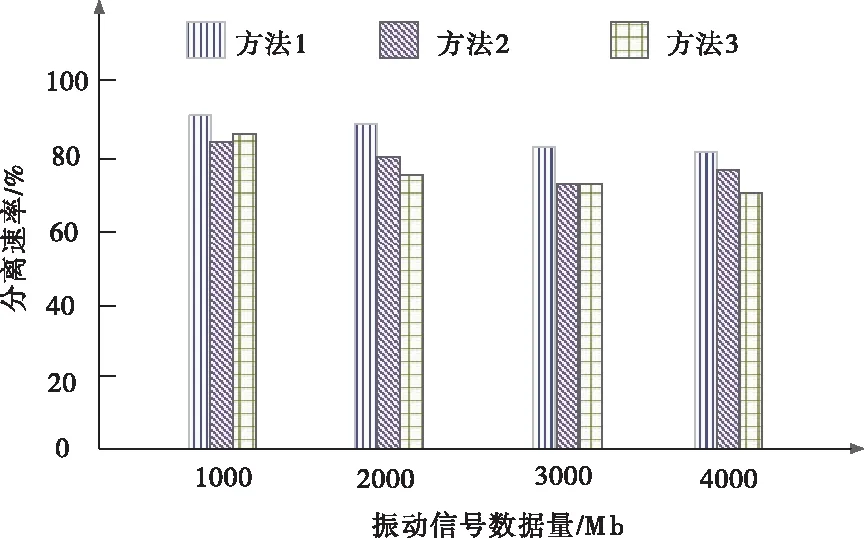
图2 不同方法的分离速率对比结果

分析图2数据可知，方法2和方法3的分离速率均低于方法1，可证明方法1的分离效率更高。这是因为方法1在对机械振动多源信号进行分离过程中，通过加权距离对机械振动信号进行去噪处理，有效地抑制了噪声污染，保持信号细节，进而提高了分离速率。

在此基础上，对比不同方法的误分率，对比结果如图3所示。

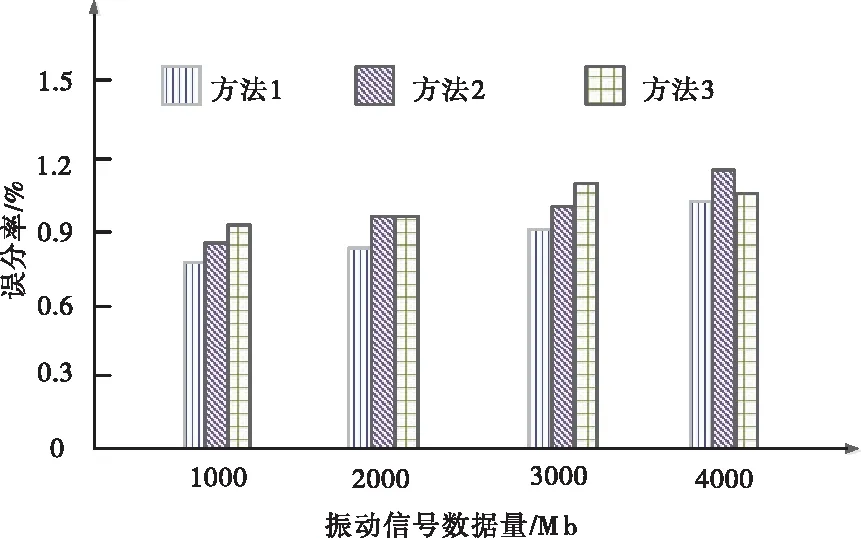
图3 不同方法的误分率对比结果

据图3数据可知，方法1的误分率要低于方法2和方法3，可证明方法1的分离准确性更高。这是因为方法1在对机械振动多源信号进行分离过程中，通过加权距离对机械振动信号进行去噪处理，有效地去除了背景噪声，提高了振动信号的可分离性，达到了较为理想的分离效果。

5 结束语

在复杂环境背景下，机械振动信号通常是由多个源信号所构成的混合信号，处于未知的背景知识下，仅仅根据各信号源相互统计独立的假设，对信号进行分离，不足以达到现代信号分离技术的标准。目前的机械振动信号分离方法没有对机械振动信号进行去噪处理，导致分离信号的信噪比较低，并存在分离速率较慢以及误分率较高的问题。针对此问题，本研究提出了基于加权距离的机械振动多源信号盲分离方法，达到了理想的分离效果。在机械设备出现异常时，其可以作为对机械设备状态识别的一个重要判断依据。