双凸极永磁电动机的建模及其系统仿真

杨天宇，张广明

(南京工业大学电气工程与控制科学学院，江苏 南京 211816)

1 引言

20世纪90年代，美国Wisconsin大学的Thomas A.Lipo教授提出了双凸极永磁电动机(Doubly Salient Permanent Magnet Motor，DSPM)[1]。DSPM结构简单、成本较低、鲁棒性强、功率密度和工作效率较高，在电动汽车、风力发电、航空航天等领域的应用日益广泛。

DSPM的建模需要在推导电机数学模型的基础上，确定电枢绕组的静态特性(自感与磁链)。静态特性的计算有三种方法：解析法、等效磁路法和有限元法。

解析法通过计算分段线性或非线性数学解析式，表示静态特性随转子位置和电枢电流变化的情况[2]，缺点是无法同时具备模型精度高和数据处理简便两种优势。等效磁路法通过求解等效磁路方程，考虑电枢反应对静态特性的影响[3]，缺点是等效磁路的构建较为繁琐。有限元法利用计算机有限元分析技术，根据电机结构和磁路特征计算静态特性[4]，精度高且计算简便，也没有解析法和等效磁路法的固有缺陷。

关于DSPM建模的研究，目前大多局限在静态特性的分析上。在仿真模型和系统构建方面的研究则较少，它们正是运用三相六状态控制[5]和三相九状态控制[6]等复杂控制策略的前提。

对此，本文建立了DSPM的仿真模型，构造了它的双闭环系统。使用标准角度控制策略[7]进行了系统仿真，仿真结果验证了电机建模和系统构造方法的有效性。

2 双凸极永磁电动机建模

2.1 数学模型推导

在结构上，定转子均为凸极结构的DSPM属于变磁阻类型电机，工作时遵循磁阻最小原理，即磁链沿磁阻最小的磁路闭合[8]。特别处在于，DSPM在定子上安装有用于励磁的永磁体，在数学模型上与普通磁阻类型电机有显著区别。

根据DSPM的磁路特征、电路特征、能量转换原理和动力学原理，推导涵盖磁链方程、电压方程、转矩方程和运动方程的数学模型。

2.1.1 磁链方程

由磁路特征，得到各相绕组磁链方程

(1)

式中：ψa，ψb，ψc为各相绕组的磁链；ψra，ψrb，ψrc为各相绕组的电枢磁链分量；ψma，ψmb，ψmc为各相绕组的永磁磁链分量；La，Lb，Lc为各相绕组的自感；Lab=Lba，Lac=Lca，Lbc=Lcb为各相绕组之间的互感；ia，ib，ic为各相绕组的电枢电流。

2.1.2 电压方程

由电路特征，得到各相绕组电压方程

(2)

式中：ua，ub，uc为各相绕组的端电压；Ra，Rb，Rc为各相绕组的电阻。

将磁链方程代入电压方程，同时因绕组间互感对计算的影响很小而将其忽略，得到各相绕组近似电压方程

(3)

式中：θ为转子位置角；ω为转子角速度。

2.1.3 转矩方程

根据机电能量转换原理，同时忽略绕组间互感引起的较小磁阻转矩分量，得到转矩方程

Te=Tea+Teb+Tec

=Tra+Tma+Trb+Tmb+Trc+Tmc

(4)

式中：Te为电磁转矩；Tea，Teb，Tec为各相输出的有效电磁转矩；Tra，Trb，Trc为各相自感磁阻转矩；Tma，Tmb，Tmc为各相永磁转矩。

2.1.4 运动方程

根据刚体定轴转动的动力学原理，得到运动方程

(5)

式中：Tl为负载转矩；J为电机转子的转动惯量；D为系统的阻尼系数。

2.2 静态特性计算

三相DSPM定、转子级数一般配置为6/4极和12/8极这两种结构。其中，12/8极DSPM拥有更高的功率密度，且轭部磁路长度和绕组端部长度较短，磁路中的铁损低、电枢中的铜耗低[9]。

DSPM中的永磁体按嵌入方式分为切向磁钢和径向磁钢。内置径向磁钢相比普通切向磁钢的优点是电机外部基本没有漏磁场。

综合上述分析，选择了12/8极内置径向磁钢的DSPM作为建模对象，其结构参数如表1所示，截面图如图1所示。

表1 DSPM结构参数

图1 DSPM截面图

运行方面，该DSPM的额定功率为550W，额定转矩为3.5Nm，额定转速为1500r/min，额定相电压为60V。

DSPM的静态特性包括各相电枢绕组的自感(忽略互感)和磁链，它们是转子位置角和电枢电流的函数。研究表明，自感和磁链主要由永磁体提供，电枢反应对其影响很小[10]，故可近似表示为转子位置角的一元函数。

在Ansys Maxwell软件中，对DSPM进行2D瞬态场有限元分析。仿真得到了空载(无电枢电流)时各相电枢绕组的自感和磁链与转子位置角(电角度)的对应关系，继而绘制相应的关系曲线。曲线中转子位置角的范围为360°电角度(45°机械角度)，且0°时的转子位置为图1中的转子位置。DSPM各相电枢绕组自感和磁链曲线如图2和图3所示。

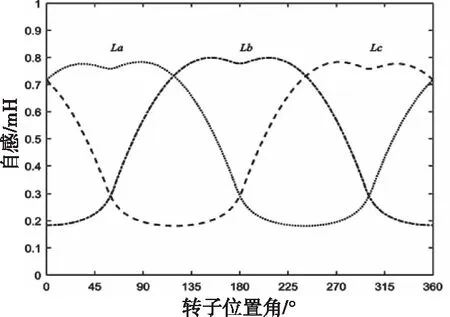
图2 DSPM各相电枢绕组自感曲线

图3 DSPM各相电枢绕组磁链曲线

根据曲线，DSPM各相电枢绕组的自感和磁链与转子位置角呈现出明显的非线性特征。

各相电枢绕组自感曲线呈马鞍状，当转子极与定子极完全重合时，铁心趋于饱和，磁阻增大，此时的自感值略小于半重合时的情况。

各相电枢绕组磁链曲线呈单峰状，随着转子极与定子极重合程度的加深，磁链值逐渐增大。

2.3 仿真模型建立

利用DSPM数学模型方程和静态特性数据，在Matlab/Simulink仿真环境中建立它的仿真模型。为计算各相电枢电流和电磁转矩，根据电机数学模型，导入有限元分析所得的自感和磁链数据，并使用数值微分方法计算它们关于转子位置角的偏导数。偏导数取值为自感和磁链数据关于转子位置角的差商。

使用模块库中的Lookup Table模块实现对自感、磁链和上述偏导数的插值。插值后自感和磁链曲线亦如图2和图3所示，自感和磁链对于转子位置角的偏导数曲线则如图4和图5所示。

图4 DSPM各相电枢绕组曲线

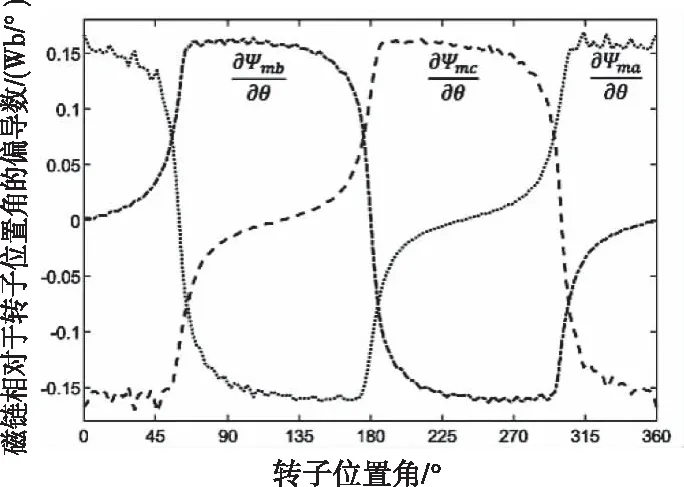
图5 DSPM各相电枢绕组曲线

各相电枢绕组模块根据电机数学模型和静态特性数据搭建而成。其中有插值模块以及表示正极和中性点的两个物理建模连接(PMC)端口。同时，转子位置信号为输入信号，端电压、相电流和相转矩信号为输出信号。

模块内部计算过程如下：首先电压测量模块测量出端电压；然后插值模块根据处理后的转子位置角，计算自感、磁链以及它们关于转子位置角的偏导数；接着将端电压代入电压方程，计算相电流；再将相电流代入转矩方程，计算相转矩；最后通过信号输出接口输出端电压、相电流和相转矩。

A相电枢绕组模块如图6所示，其它相的电枢绕组模块与A相类似。其中，电枢绕组的电阻R取值为0.28Ω。

图6 DSPM的A相电枢绕组模块

DSPM的运动方程仿真模型如图7所示。其中有一个表示电磁转矩的信号输入端口，以及两个表示转子转速和位置角的输出端口。根据实际情况，转子的转动惯量J取值为0.002kg·m2，系统的阻尼系数D取值为0.001N·m·s。

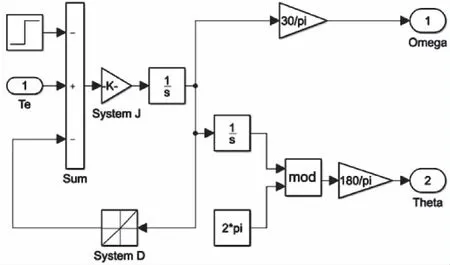
图7 DSPM的运动方程模块

上述各相绕组和运动方程模块共同构成了DSPM的仿真模型。该模型如图9中的DSPM模块所示，其输入为三相电枢绕组及其中性点的物理建模连接端口，输出为三相电枢绕组的相电压、相电流，转子的位置角、转速，以及电机的电磁转矩。

3 双凸极永磁电动机系统仿真

3.1 系统模块化构造

DSPM系统框图如图8所示。该系统的控制方式为双闭环控制。其中外环为转速环，使用PI控制，内环为电流环，使用滞环控制。

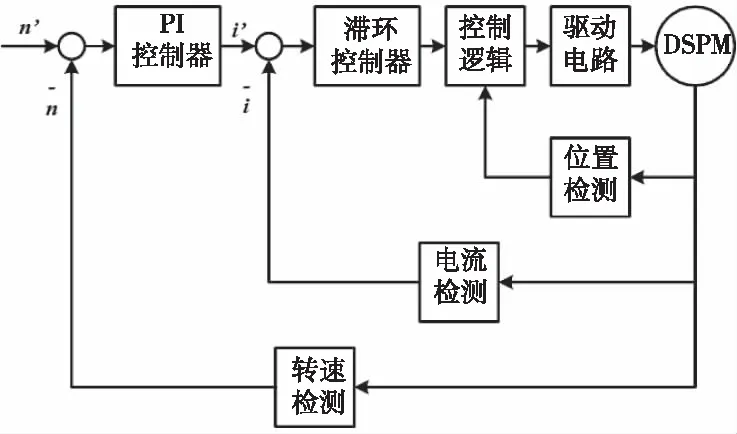
图8 DSPM系统框图

同时，DSPM是方波驱动型电机，采用标准角度控制策略，即在电枢绕组磁链的上升区间和下降区间内分别通入正负电流，在磁链接近为零的区间内不通电[7]。系统根据此策略，将检测的转子位置转换为驱动电路中开关管的控制逻辑。

在Matlab/Simulink仿真环境中建立DSPM系统。按照模块化的构造思想，将系统划分为控制、驱动和DSPM三个主要模块，各模块便于集成和扩展。系统仿真结构图如图9所示。

图9 DSPM系统仿真结构图

3.1.1 DSPM模块

DSPM模块如图10所示，它建立了DSPM精确仿真模型，其中包括各相绕组和运动方程子模块。同时将各相电流、转子转速和位置角信号反馈至控制模块。

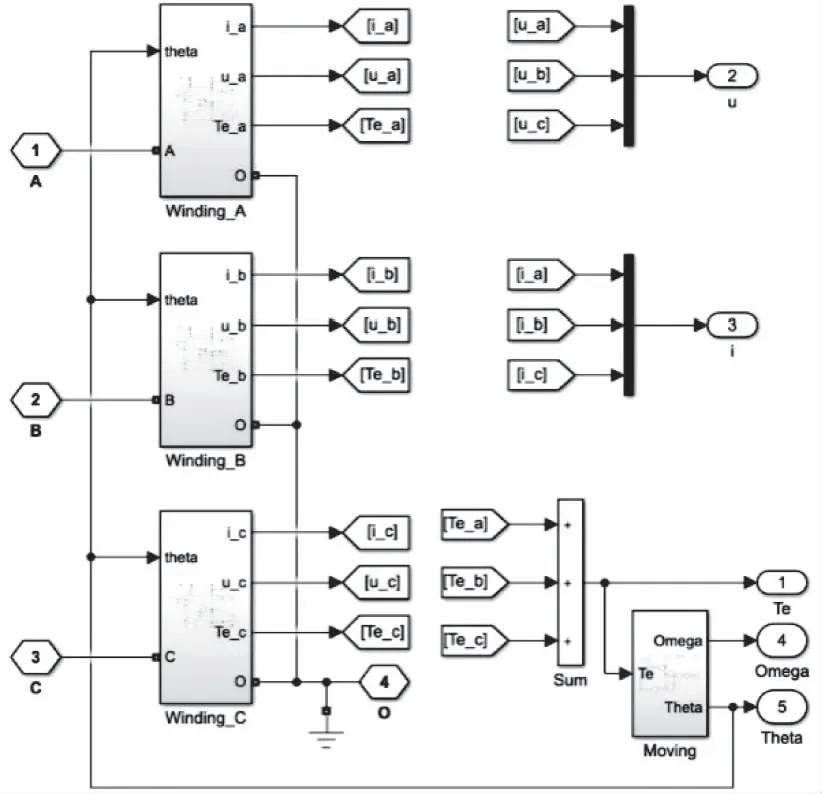
图10 DSPM模块结构图

3.1.2 驱动模块

驱动模块如图11所示，它构造了三相桥式逆变电路，其直流侧电压为120V，使用分裂电容均压，门极驱动信号由输入端发送至各功率晶体管，驱动电压由输出端提供至DSPM模块。

图11 驱动模块结构图

3.1.3 控制模块

控制模块接收DSPM的反馈信号，生成驱动信号传递至驱动模块，模块内部分为三个部分。

双闭环控制部分如图12所示，该部分接收转速和电流信号，经PI和滞环控制器，输出各相PWM信号以及与参考电流同号的方向信号。方向信号为正1表示电动，为负1表示制动。PI控制器中Kp=0.064，Ki=0.8。为防止出现过流现象，参考电流限幅在±60A区间。

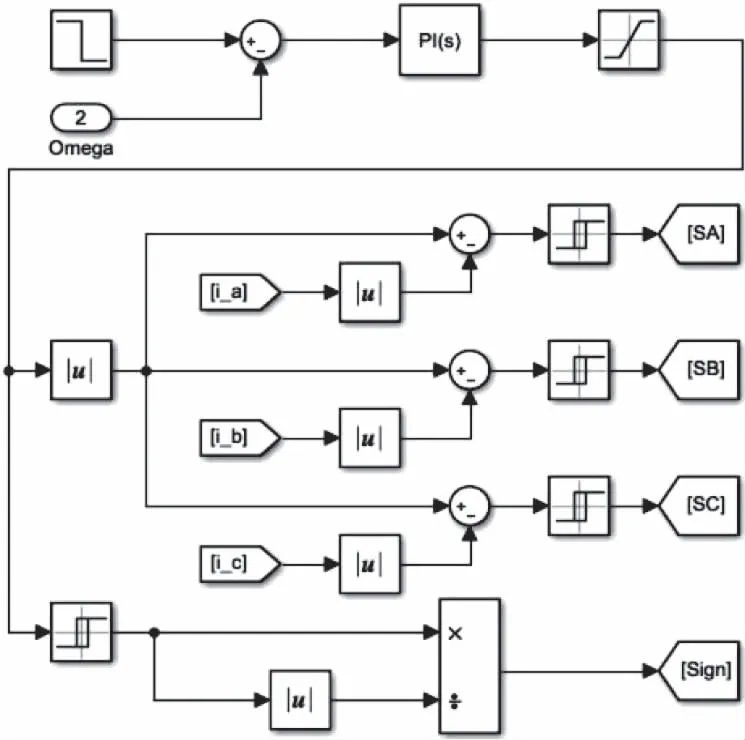
图12 双闭环控制部分模块图

标准角度控制部分如图13所示，该部分接收转子位置信号，根据标准角度控制策略，输出驱动电路中开关管的导通信号。

图13 标准角度控制部分模块图

驱动信号输出部分如图14所示，该部分将转向信号、各相PWM信号和开关管导通信号转化为开关管驱动信号。

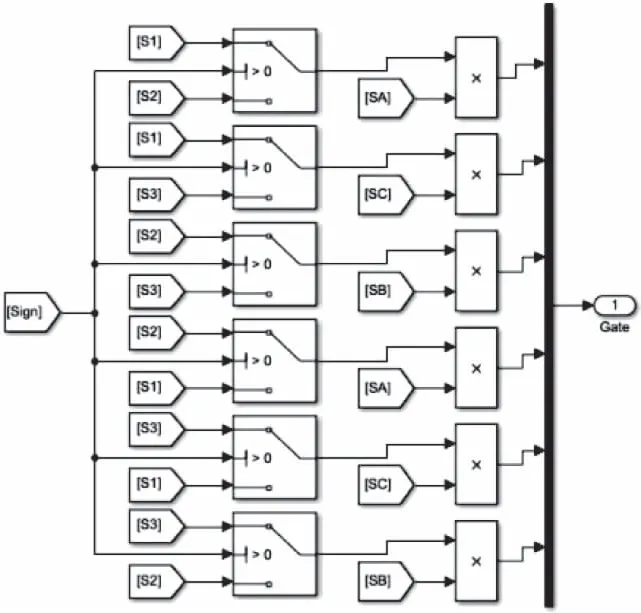
图14 驱动信号输出部分模块图

各转子位置下，DSPM电动和制动运行时开关管的标准角度控制策略如表2所示。

表2 标准角度控制策略

3.2 系统仿真分析

对DSPM系统进行仿真，将其运行划分为三个运行阶段。各阶段的时间、参考转速和负载转矩如表3所示。

表3 DSPM各阶段运行状态

经过仿真，DSPM的实际转速、A相电流、电磁转矩波形如图15所示。

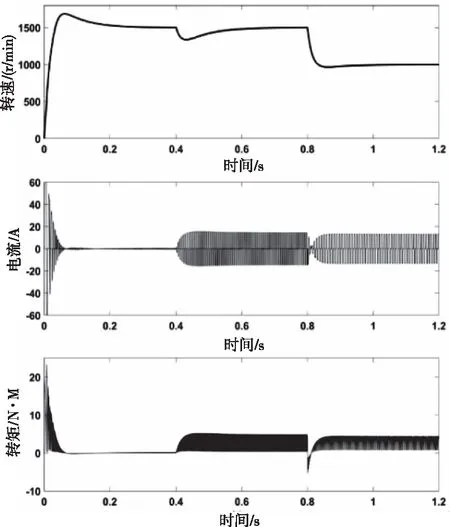
图15 实际转速、A相电流、电磁转矩波形图

三个阶段中，电机实际转速均较快地达到了准确的参考转速。阶段I中，电机空载起动，起动电流被限幅至±60A，随后电流和转矩衰减至稳定。阶段II和阶段III中，电机负载运行，且前者的电流和转矩比后者大。综合上述波形和分析，验证了DSPM仿真系统整体的有效性。

额定状态下DSPM三相电流波形如图16所示。三相电流呈方波状，任意时刻，两相通正负电，另一相不通电，符合标准角度控制策略。同时由于各相自感大小的差异，使得换相时电流下降时间比上升时间长。

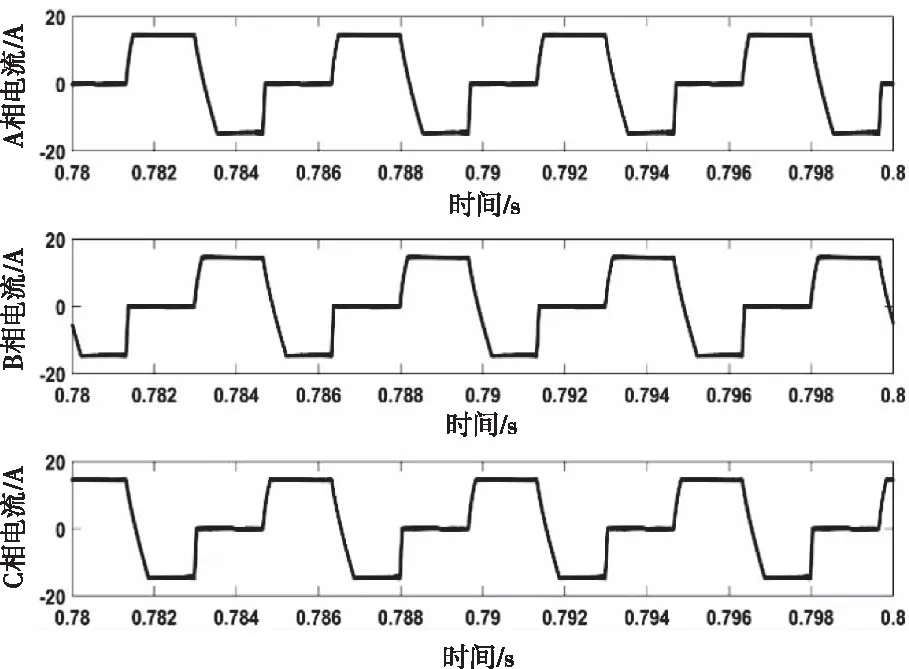
图16 额定状态下三相电流波形图

额定状态下DSPM三相转矩与合成转矩波形如图17所示。各相转矩和电流存在互相对应的关系，转矩在对应绕组通电时产生，不通电时消失，换向时减小。合成转矩由各相转矩叠加而成。各相转矩在换相时减小，形成合成转矩典型的脉动状波形。

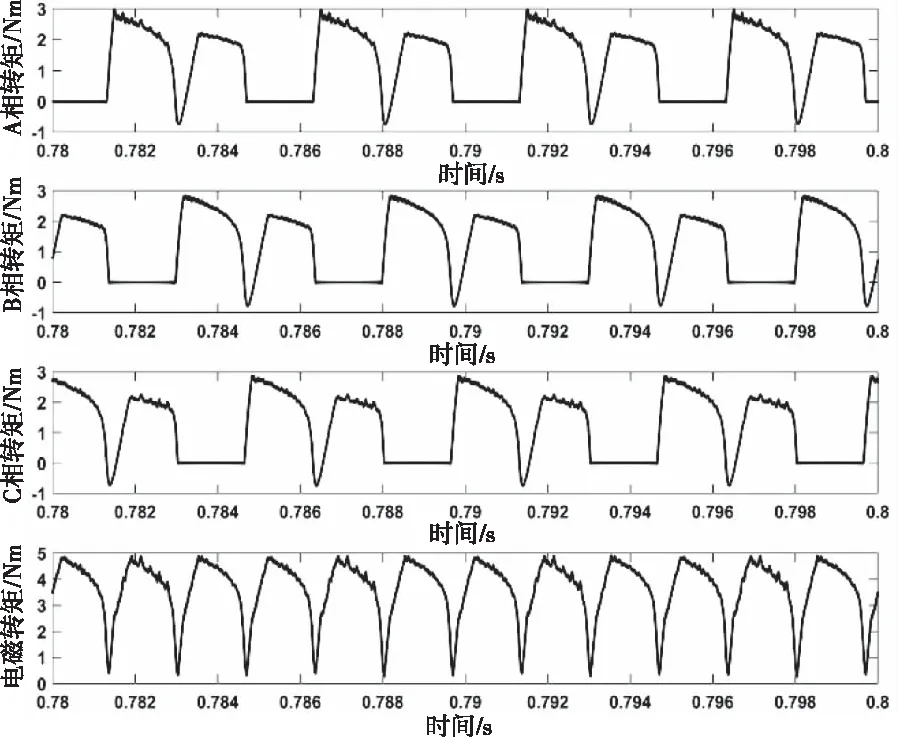
图17 额定状态下三相转矩与合成转矩波形图

综合上述波形和分析，验证了DSPM仿真模型建立的准确性。

4 结论

1)所分析12/8极内置径向磁钢的DSPM具有高功率密度、低铁损、低铜耗的优点；

2)使用有限元法计算电机静态特性，代入推导的数学模型方程，建立了DSPM仿真模型，此方法精度高且通用性强；

3)构造了DSPM完整的双闭环系统，并仿真验证了系统的有效性。该系统模块化程度高且实用性强，便于集成和扩展，为研究复杂控制策略和提升控制性能提供基础。