参数控制多涡卷超混沌吸引子及其应用*

杨永明，陈世强，李 强

(1.湖北民族大学新材料与机电工程学院，湖北 恩施 445000；2.湖北民族大学新材料成型及装备技术产学研中心，湖北 恩施 445000)

1 引言

混沌因其具有确定性、类随机性、对初值的敏感性等特点而广泛应用于工程领域[1-5]。动力学行为丰富的混沌系统应用于加密领域时，安全性更高[6，7]。

超混沌具有比混沌更丰富的动力学行为，在图像加密、保密通信等领域具有相当的应用潜力[8-10]。构造超混沌的常用方法是[11-17]：改进一个混沌系统使其变成超混沌系统；改进一个超混沌系统使其成为另一个超混沌系统；直接构造新的超混沌系统。文献[11]通过改进经典Lü系统并引入忆阻元件，提出了一种基于忆阻的改进型超混沌Lü系统，其特点是不存在任何平衡点。文献[12]利用Cat映射的Lyapunov指数与相关Cat矩阵之间的内在联系提出了一种简单而有效的构造超混沌的方法，该方法可构造具有任意个正Lyapunov指数的超混沌。文献[13]提出了一种新的具有多动态特性的四维超混沌系统，系统具有平衡线或不稳定的平衡点，通过改变系统参数可以改变其特性。文献[14]构造了一种简单的四维超混沌混沌系统，系统只有一个稳定的平衡点，能表现出包括混沌，周期性，稳定性以及各种吸引子共存的各种动态行为。文献[15]基于三维广义Lorenz系统开发了一种无平衡点超混沌系统，并在新系统的基础上构造了一个没有平衡点复杂超混沌系统，两个新系统都具有隐藏吸引子，且能呈现各种动态行为。文献[16]提出一种基于肖克利二极管模型、且具有双曲正弦非线性的四维连续时间自治超混沌系统，系统可经历周期态、准周期态、混沌态及超混沌态，具有丰富的动力学行为。文献[17]在原系统的基础上，受“平行宇宙理论”的启发，通过引入三角函数构造了一种具有复杂动态行为的四维自治超混沌系统，系统具体无限平衡点，与原始系统相比，系统对初始值更敏感。

此外，增加吸引子涡卷数量也能丰富混沌系统的动力学行为[18-21]。目前，一类常用的方法是利用函数序列生成多涡卷吸引子，如采用饱和函数序列、双曲正切函数序列、非线性调制函数序列、阈值函数序列等[6]。文献[22]最早提出了变参数变涡卷的方法，在不改变函数的情况下，通过改变系统参数就可以改变涡卷数量，但该文献提出的只是三维混沌系统，其动力学行为还可以进一步丰富。

本文构造了一种四维多涡卷超混沌系统，在不改变分段线性函数的情况下，通过修改系统参数可实现涡卷数量的改变。相对于文献[11]-[17]，本文系统具有更多的涡卷数量，动力学行为更丰富。相对于文献[22]，本文系统具备更多维度，动力学特性更复杂。分析结果表明，本文系统用于图像加密时安全性高。

2 多涡卷超混沌吸引子

文献[22]提出的基于Chua系统的参数控制多涡卷混沌吸引子描述为

(1)

其中，a、b、c、d、g为控制参数，x、y、z为状态变量，且均为实常数，f(x)描述为

f(x)=sgn(x)+sgn(x+b)+sgn(x-b)+

sgn(x+2b)+sgn(x-2b)

(2)

本文在系统(1)的基础上，增加状态反馈控制器w，同时增加控制参数h、m、n。为避免计算过程中的奇点，用tanh(100x)函数替换sgn(x)函数[22]。改进后的系统为

(3)

其中F(x)描述为

F(x)=tanh(100x)+ tanh(100(x+b))

+ tanh(100(x-b))+ tanh(100(x+2b))

+ tanh(100(x-2b))

(4)

保持参数b=7不变，即函数F(x)不变，改变其它系统参数时，可得到不同涡卷数量的混沌。表1中给出了涡卷数量与对应的系统参数以及用各组参数计算出的李氏指数，各组参数对应的x-y相图如图1所示，其中计算李氏指数和画相图时所选初始值IC=(1，1，1，1)。表中各组参数所对应的四个李氏指数均为(+，+，0，-)的形式，说明各组参数下的系统均为超混沌系统。

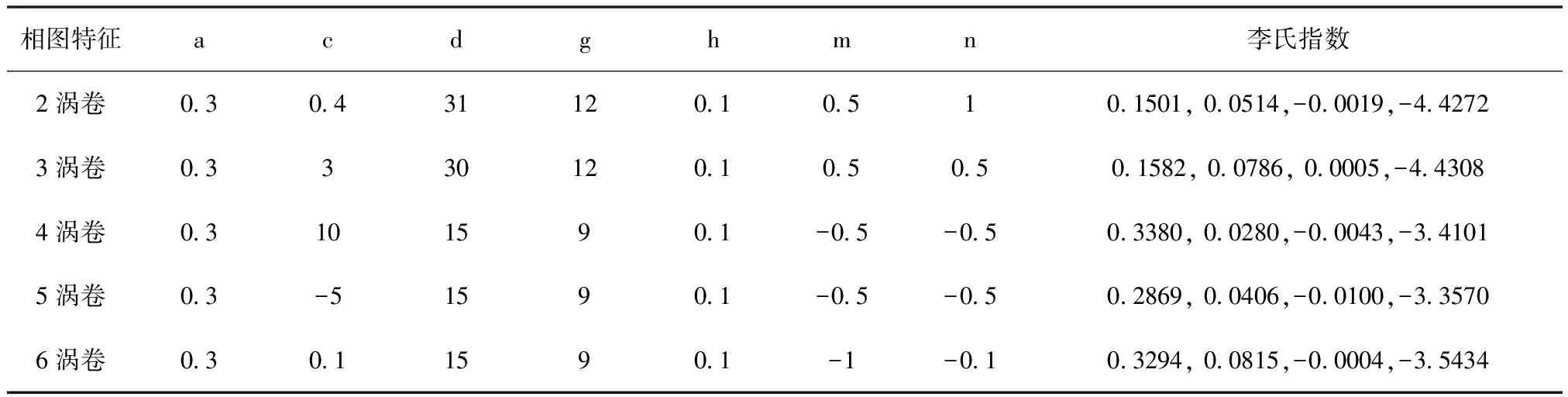
表1 不同涡卷数量对应的系统参数及李氏指数

图1 不同数量涡卷对应的x-y相图

3 系统动力学分析

3.1 对称性与耗散性

从系统方程(3)中不难发现，系统不具备对称性。而根据系统(3)，可得

(5)

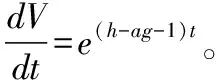
3.2 平衡点分析

令方程(3)右边等于零，即

(6)

分别代入表中产生2涡卷至6涡卷对应的参数，可以计算出对应的平衡点及特征值。例如，产生2涡卷时有4个平衡点，分别为S1=[-31.07，-4.29，26.78，-267.82]，S2=[-6.24，-0.84，5.4，-54.02]，S3=[6.17，0.89，-5.29，52.87]，S4=[31，4.33，-26.67，266.67]，4个平衡点对应的特征值均为λ1=-4.7516，λ2=0.0642，λ3，4=0.0937±4.7764i，λ1为负实数，λ3，4的实部为正，因此这4个平衡点为不稳定的鞍焦点；再如，产生5涡卷时有3个平衡点，分别为S1=[-28.46，-4.09，24.37，121.85]，S2=[-3.01，-0.46，2.55，12.76]，S3=[35.17，5.00，-30.18，-150.88]，3个平衡点对应的特征值均为λ1=-4.0219，λ2=0.0631，λ3，4=0.1794±3.1180i，λ1为负实数，λ3，4的实部为正，因此这3个平衡点均为不稳定的鞍焦点。

对于产生2涡卷时的这组参数，进一步研究发现，当初始值IC=(1，1，1，1)时，利用该组参数可生成2涡卷吸引子，而当初始值IC=(0，0，0，0)时，利用该组参数可生成4涡卷吸引子，如图2所示。说明系统具有多稳态共存的特性[23]。

图2 初始值IC=(0，0，0，0)时的x-y相图

对于产生5涡卷时的这组参数，系统生成了5涡卷吸引子，但该组参数对应的平衡点只有3个，说明系统处于隐藏振荡状态，生成了隐藏吸引子[24]。

3.3 李氏指数谱

利用表1中生成2涡卷吸引子的参数，并令d在20至70之间变化，可得到系统随参数d变化的李氏指数谱，如图3所示，计算时初始值IC=(1，1，1，1)。从图3中可以看出，当d∈[20，22.8]时，四个李氏指数的形式为(+，0，-，-)，说明系统处于混沌状态，当d∈[22.9，35]时，李氏指数的形式为(+，+，0，-)，说明系统处于超混沌状态，d∈[52.4，53]时，李氏指数的形式为(0，0，-，-)，说明系统处于准周期状态，d∈[64，70]时，李氏指数的形式为(0，-，-，-)，说明系统处于周期状态。可见，当参数d在20至70之间变化时，系统经历了周期态、准周期态、混沌态及超混沌态，表现出复杂的动力学行为。

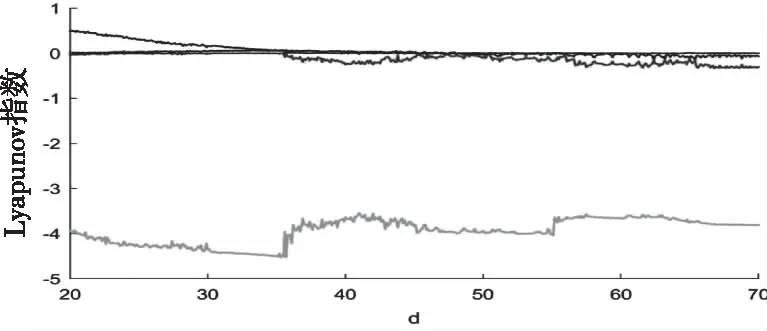
图3 系统随参数d变化的李氏指数谱

4 系统电路实现

为了验证系统(3)在工程应用中的可行性，以5涡卷系统为例，采用OrCAD PSpice软件设计了系统的电路，如图4所示，仿真结果的x-y相图如图5所示。观察实验结果可发现电路仿真与数值仿真结果是一致的，从而验证了本文提出的超混沌模型在物理上是可以实现的。

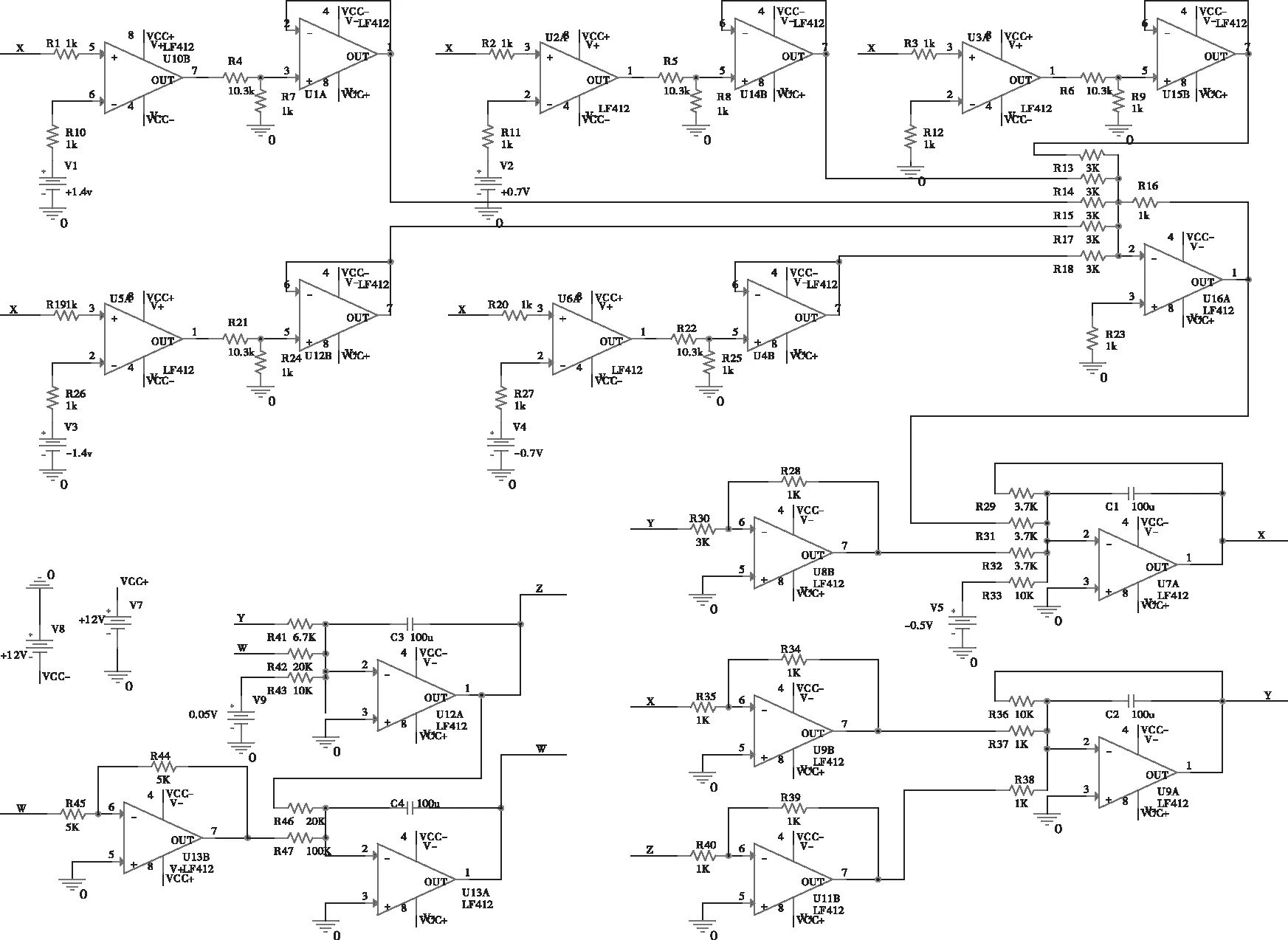
图4 系统仿真电路

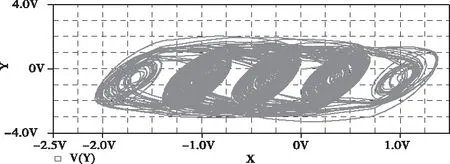
图5 电路仿真x-y相图

电路中运算放大器采用LF412，其供电电压为±12VDC，为避免输出失真，将状态变量按式(7)作线性变换，变换后的系统为(8)，F(x)为(9)，电路的状态空间方程为(10)。组成F(x)的五个符号函数中，每个tanh(100x)函数由两个运算放大器及其外围元器件实现，如U10B、U1A、R1、R4、R7、R10、V1组成了tanh(100(x-1.4))，U10B的输出经R4、R7分压后由跟随器输出。当供电电压为±12VDC时，LF412的输出电压范围为-11.3V至+11.3V，为使U1A输出为+1V或-1V，需要满足R4:R7=10.3:1，由此可确定R4、R7的阻值。根据以上分析可确定所有元件参数，如表2所示。

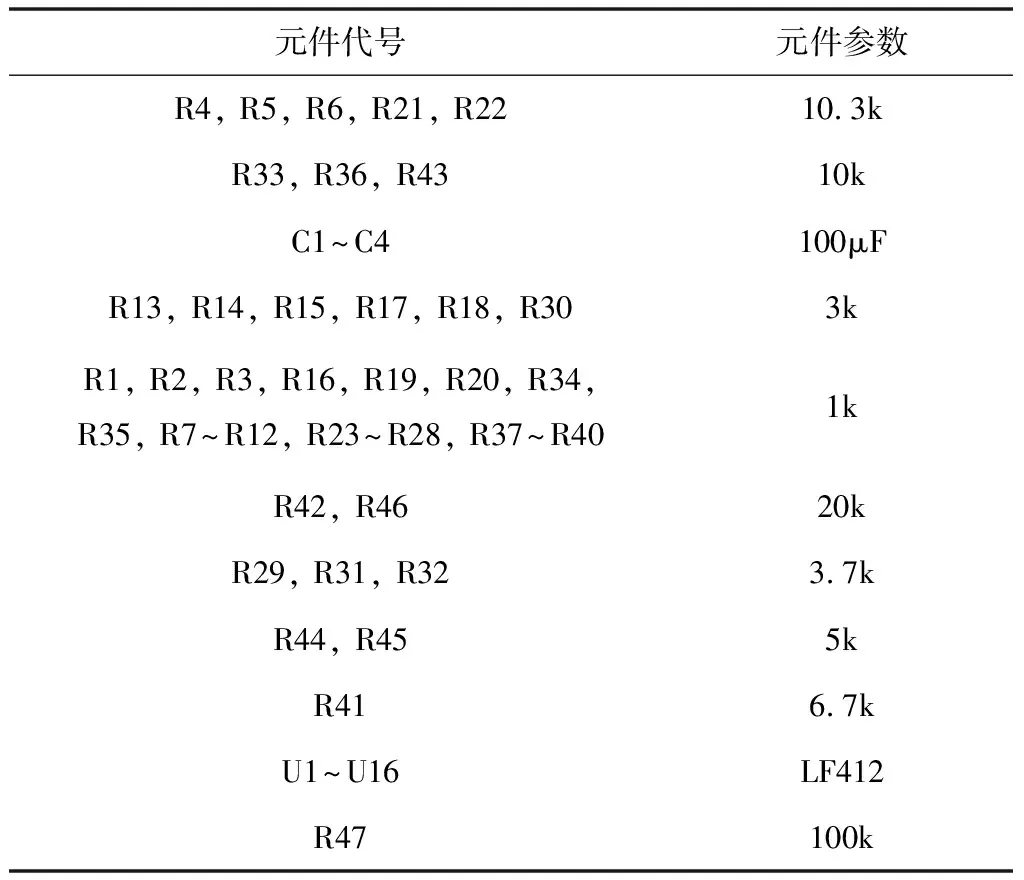
表2 元件参数

(x，y，z，w)→(10x，y，10z，10w)

(7)

(8)

F(x)=tanh(100x)+ tanh(100(x+0.7))

+ tanh(100(x-0.7))+ tanh(100(x+1.4))

+ tanh(100(x-1.4)

(9)

(10)

5 参数控制多涡卷超混沌吸引子在图像加密中的应用

混沌系统因具有初值敏感性、类随机性和不可预测性常用于图像加密，本文将提出的参数控制多涡卷超混沌系统也用于了图像加密，并取得了良好的加密效果。

5.1 加密及解密原理

对于给定的灰度图像，首先对图像中每个点的像素值进行替换，且偶数位置的点和奇数位置的点分别基于X相和Y相混沌序列进行像素值替换，之后基于Z相混沌序列对像素位置置乱，加密流程如图6所示，加密步骤如下。解密过程是加密过程的逆过程。

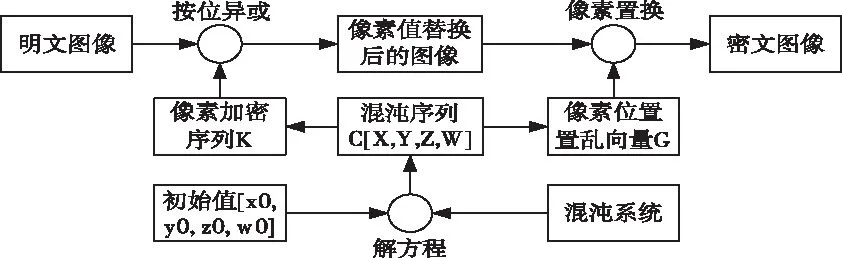
图6 加密流程

Step1：输入明文图像A，像素大小为M×N，令L=M×N。

Step2：用初始值(密匙)[x0，y0，z0，w0]求解微分方程，取其中长度为L的四组混沌序列C[X，Y，Z，W]。

Step3：按公式求取像素值加密序列K

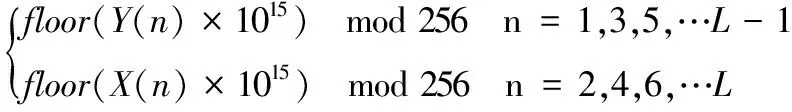
(11)

Step4：将K转换成M×N的矩阵，将该矩阵中的每一个元素与矩阵A中的每一个元素进行按位异或运算得到图像A1。

Step5：对Z组中的所有元素分别进行放大1015倍、向负无穷方向取整、对L取模运算，再对元素进行升序排序，将排序得到的位置向量G作为像素位置置乱向量。

Step6：将A1转换成一维行向量P，按公式将图像中的像素进行置换得到P1，将P1转换成M×N的矩阵得到加密后的图像A2。

P1(i)=P(G(i))，1≤i≤L

(12)

5.2 实验结果

实验以经典的lena灰度图像为例，其像素值为512×512，采用本文算法对图像进行加密及解密，算法中采用的混沌系统为系统(8)，混沌初始值(密匙)Key1=[0.2 0.5 0.3 0.1]，图7为原图、加密图像及解密图像的对比。从图7中可以看出，加密图像杂乱无章，完全失去原图信息，而解密图像与原图完全一致，说明算法能正确实现图像的加密及解密。

图7 图像加密与解密结果

5.3 密匙敏感性分析

密文图像的变化率(The change rate of cipher text，CRC)可以反映密匙的加密敏感程度。用正确密匙Key1=[0.2，0.5，0.3，0.1]对lena原图进行加密得到密文图像A1，如图8(b)，用错误密匙Key2=[0.200000000001，0.5，0.3，0.1]对lena原图进行加密得到密文图像A2，如图8(c)，计算得A1和A2的图像变化率为99.61%。图8(a)为原图，图8(d)为用Key1对A1进行解密的结果，图8(e)为用Key2对A1进行解密的结果。说明即使密匙发生微小变化时，密文图像变化率也能接近100%，而用错误密匙得到的解密图像与原图的关联性也无法看出，说明算法对密匙极为敏感。

图8 密匙敏感性测试结果

5.4 直方图分析

直方图可以反应图像像素值分布是否均匀，密文图像直方图越平坦则像素值分布越均匀，抵御灰度统计分析攻击的能力也越强。图9(a)示为lena原图直方图，图9(b)为lena密文图像直方图，对比可发现，密文图像直方图的灰度均匀性明显优于原文图像，具有良好的抵御灰度统计分析攻击的能力。

图9 直方图分析结果

5.5 相关性分析

一副正常的数字图像中，相邻的两个像素点的灰度值是很接近的，图像的相关系数可达0.9，经过加密后的图像中，相邻的两个像素点的灰度值不应具有明显相关性，相关系数越接近0说明加密效果越好。在lena原图中随机取1000个点，利用文献[25]中的公式计算得其水平、垂直和对角线方向的相关性分别为0.9733、0.9870、0.9603，在lena加密图像中随机取1000个点，计算得其水平、垂直和对角线方向的相关性分别为0.0153、0.0034、0.0101，说明原图的相关性极强，加密后的相关性极弱。这表明原始图像的统计特征已经被扩散到密文图像中。

5.6 信息熵分析

信息熵反应了图像灰度值分布是否均匀，灰度值分布越均匀信息熵越大，其理论值是8。计算得lena原图的信息熵为7.4455，lena加密图像的信息熵为7.9992，接近理论值8，说明图像像素值分布很均匀，加密效果良好。

5.7 抗攻击能力分析

为测试算法的抗攻击能力，对加密图像进行了剪切攻击。剪掉加密图像中间180×180大小的图像，如图10(b)所示，再对剪切过的图像进行解密，解密图像如图10(d)所示。图10(a)为剪切前的加密图像，图10(c)为剪切前加密图像的解密图像。对比图10(c)和图10(d)可以发现，图10(d)中均匀分布有一些错误的像素点，但仍然可以清晰辨认原始图像信息。说明加密图像在遭受攻击后仍然具有良好的解密效果。

图10 抗攻击能力分析结果

6 结论

本文通过增加线性反馈项构造了一种四维多涡卷超混沌系统，在不同参数下可表现出2涡卷到6涡卷超混沌吸引子。理论分析表明，系统是耗散的，在一定参数范围内，系统具有两个正李氏指数，处于超混沌态，表现出复杂的动力学行为；系统电路仿真结果与数值仿真结果一致，说明系统在物理上可以实现；对系统进行了图像加密应用，密文相关性低于0.02、信息熵大于7.999，密匙变化10-11时，密文的变化率达99.61%，且具有良好的抵御灰度统计分析的能力和抗攻击能力，说明将超混沌系统用于图像加密时安全性高。