基于PN序列互相关同步低复杂度实现方法
付博炜,李明齐
(1.中国科学院上海高等研究院,上海 201210;2.上海科技大学信息学院,上海 201210;3.中国科学院大学,北京100049)
1 引言
在无线通信中,信号的同步至关重要,错误的定时同步可能会产生符号间的干扰(ISI),错误的频率同步会产生载波间的干扰(ICI),从而降低系统的性能[1]。现有的无线通信系统中常常加入特定的辅助信号用于同步[2]。文献[3,4]提出了基于自相关的同步方法,尽管实现简单,但在低信噪比的情况下,由于自相关运算受限于噪声,使得该方法的时频同步性能较差[10]。文献[5]使用互相关同步算法将接收信号与本地序列做互相关运算,由于本地序列不受噪声影响,相关峰值尖锐,抗干扰能力强,在低信噪比条件下,比自相关同步精度更高[8,9]。但是,相比于自相关同步,互相关的计算不依赖历史结果,计算复杂度高,需要大量并行运算,不利于实际工程实现。文献[6,7]使用时域伪随机码(PN code)作为辅助序列,由于PN序列的值只有1和-1,在互相关实现上,可以将复杂的复数乘法简化为数据选择(MUX),降低实现的复杂度。但在低信噪比工作时需要长训练序列的情况下,大量的加法运算仍会带来巨大的开销。
针对在长训练序列情况下基于PN码互相关同步方法实现复杂度仍然较高的问题,本文设计了一种基于PN码序列的近似互相关同步(PNACCS)实现方法。该方法使用近似加法器替换传统方法中的二元加法器,降低了互相关同步算法的实现复杂度,但其时频同步性能与传统互相关几乎相同。
2 系统模型
使用的前导辅助序列结构与文献[6]中相似,训练序列为p=[ABAB],其中A,B为长度为N的时域PN序列。
对于发送信号p(n),接收的离散基带信号为
(1)
其中h(l)代表第l条多径信道,d是接收信号的时间偏移,τl为第l条径的延时。ε为归一化载波频偏,w(n)为均值为零的加性高斯白噪声。
接收信号与本地第i(i=1,2,3,4)段训练序列,分别对应(ABAB)的互相关输出为
(2)
定时同步判决测度为
(3)
根据判决门限θ,估计的定时同步结果为
(4)
根据定时同步结果,估计的归一化频偏为
(5)
接收机的同步算法实现结构如图1所示,由互相关、定时同步、频偏估计3个部分构成。互相关器将接收序列与本地序列进行滑动互相关,将即时的相关结果传递给定时同步和频偏估计。定时同步将相关结果与门限进行比较,判定信号的起始位置。频偏估计部分将互相关结果运用cordic算法求得偏移角度,得到归一化频偏,根据信号起始位置和归一化频偏对接收到的信号进行频偏补偿。
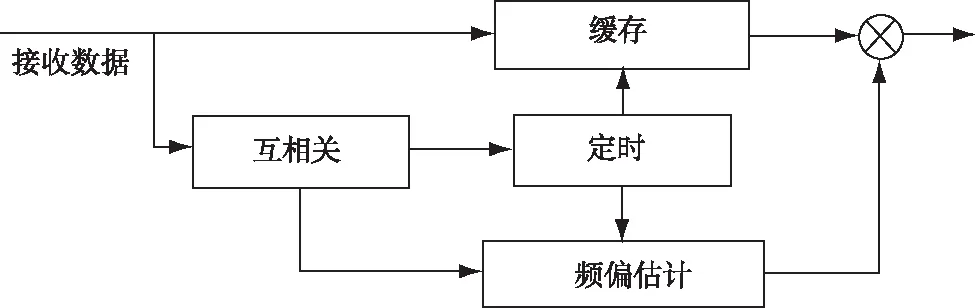
图1 基于互相关的同步结构
3 PNACCS方法中互相关模块的实现和优化
3.1 近似加法器的设计和实现
对于长度为4N的训练序列,每个采样时刻需要计算2N点的互相关结果并进行存储。由于训练序列的值只有1和-1,式(2)中的乘法可以转换成逻辑操作。大量的加法器是互相关实现中的主要开销。
与传统互相关方法相比,改进方法在实现结构中将互相关运算中部分全精度加法器用复杂度优化的近似加法器进行了代替。
图2(c)是文献[11]提出的一种四输入一输出的四元近似加法器,相比于图2(a)中给出的传统二输入一输出的二元加法器,图2(b)中主流FPGA提供的一种三输入的三元加法器结构,三种加法器结构在FPGA中都只占用一个ALUT(Altera)/quarter-slice(Xilinx)逻辑资源,但近似加法器以损失部分进位精度为代价,处理的数据更多,在加法树的实现中占用的逻辑资源最少。
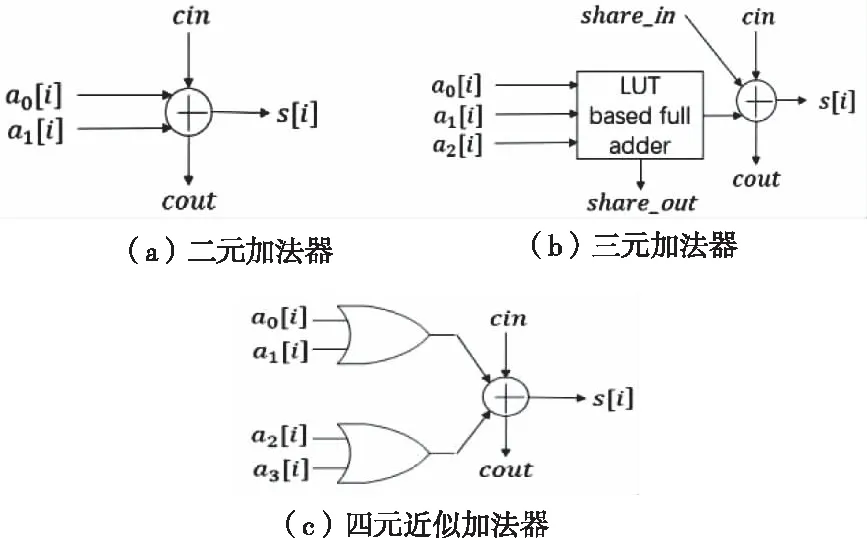
图2 常用加法器和近似加法器的实现结构
图3为PNACCS采用的基于近似加法器的互相关结构。由于在同步算法中,互相关运算的结果主要用于判断和估计,能容忍一定的计算误差,因此,PNACCS方法的互相关器在三元加法器和四元近似加法器的基础上,将接收的数据分为高位和低位两部分。数据的高位部分的计算全部采用精确的三元加法器,而低位部分的计算可以在第一层使用近似加法器以减少实现的复杂度,最后将两部分的计算结果加上先验的误差补偿得到最终的互相关输出。
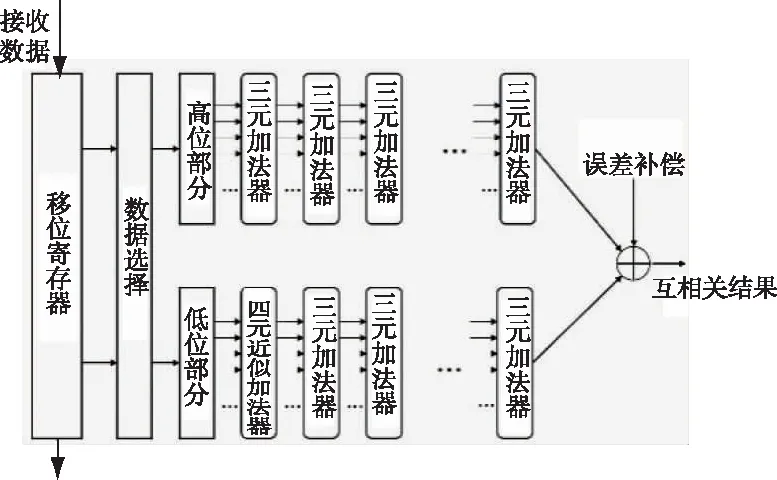
图3 基于近似加法器的互相关结构
3.2 近似加法器的误差补偿以及低位位宽对同步性能的影响
在自动增益控制(AGC)的作用下,ADC接收的信号将处于一个稳定的范围,接收数据的低位部分将满足均匀分布,当相关窗口N足够大时,根据中心极限定理,低位部分近似计算的误差e可以近似为正态分布e~N(Lμ,Lσ2),μ,σ与低位位宽P有关,L=N/4为四输入近似加法器个数。根据近似加法器的结构可得近似误差的均值和方差参数为
μ=2P-1-0.5
令误差补偿为Lμ,补偿后近似加法器产生的误差为e~N(0,Lσ2),在低信噪比的情况下,误差功率Lσ2远小于信道噪声。对同步性能影响较小,合理地选择低位位宽P可以在同步性能和实现复杂度间获得一个折衷。
4 性能分析与仿真结果
4.1 PNACCS方法的时频同步性能
为验证3.2节中结论以及PNACCS方法的可行性,合理选择低位的位宽,本文对位宽P的PNACCS方法的时频同步性能进行仿真验证。针对极低信噪比的情况,使用N=4096的相关长度。ADC接收数据位宽为14位,归一化频偏ε=0.1。选择合适判决门限θ使得虚警概率PFA≈10-3。在加性高斯白噪声(AWGN)信道和ITU-VA多径信道下进行仿真[13]。仿真次数为12000次/SNR。
根据序列结构和多径信道特性,当定时同步误差小于4个采样点时,性能损失较小,可以认为定时同步成功。图4和图5比较了不同位宽P的PNACCS方法在AWGN信道和多径信道下的同步检测概率PD。从仿真结果中可以看出,在信噪比较高的情况下,PNACCS方法没有定时性能的损失,在信噪比较低的情况,同步性能会随着低位位宽P的增加而下降,但在P<=8时,性能损失小于0.01。
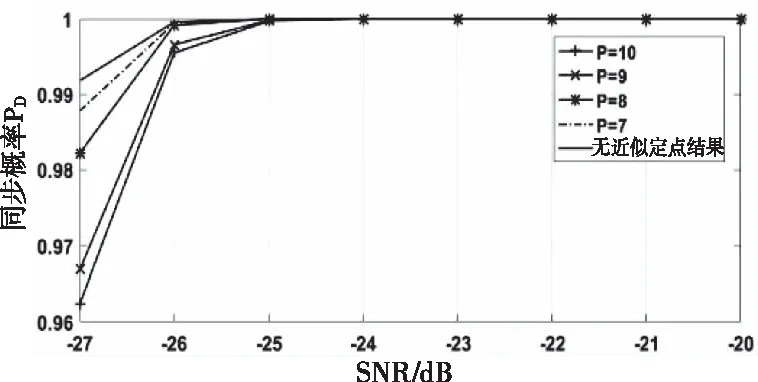
图4 AWGN信道下定时同步性能
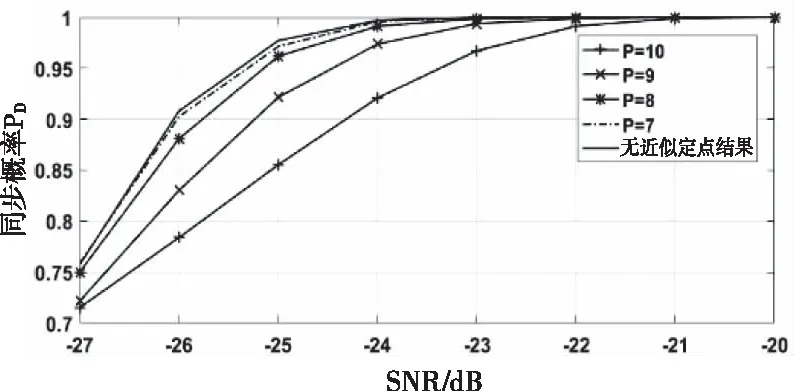
图5 多径信道下定时同步性能
图6和图7比较了不同位宽P的PNACCS方法在AWGN信道和多径信道下频偏估计的性能。从仿真结果可以看出,该方法的频偏估计性能随着位宽P的增加而下降。当位宽P=7时,频偏估计性能几乎没有损失,当P>=9时,频偏估计性能损失较大。在信噪比较高,估计性能较好的情况下,可以选择低有效位的位宽P=9以降低实现复杂度。在信噪比较低,估计性能较差的情况下,选择低有效位的位宽P=7以降低估计误差。
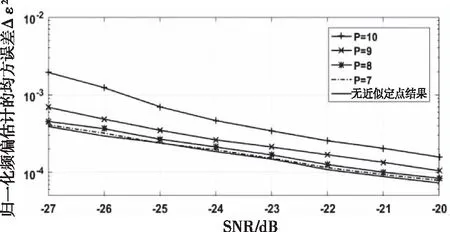
图6 AWGN信道下频偏估计性能
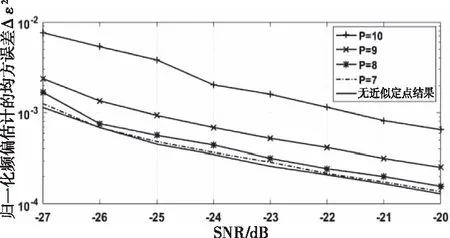
图7 多径信道下频偏估计性能
4.2 PNACCS方法的实现复杂度
在Altera FPGA中,图3所示的三种加法器结构在实现时都占用一个自适应查找表(ALUT)的逻辑资源。互相关器中使用的加法器越多,实现就越复杂。对位宽为W,长度为N的复数相关器,基于二元加法器实现,需要二元加法器的数量为:
使用三元加法器实现,三元加法器的数量为
而使用低位位宽为P的部分近似加法树,需要三元加法器和近似加法器的总数量约为
从表达式中可以看出,使用三元加法器和部分近似加法树的方法资源占用要远少于传统二元加法器的方法,而且随着低位位宽P的增加,部分近似加法树的方法将进一步减少实现的复杂度。
为验证上述分析,将量化位宽W=14,长度为N=4096的复数相关器基于以上三种结构的分别在Altera Stratix V 5SGSD8 FPGA上实现,通过Quartus II软件平台进行综合。
实现结果如表1所示,由于实际实现中一些逻辑控制、位宽扩展以及综合上的优化,实际结果比理论结果占用资源略有提升,但与理论分析基本相符。在Altera FPGA中,综合了自适应查找表(ALUT),全加器以及寄存器的自适应逻辑模块(ALM)是FPGA的基本逻辑资源。相较于比较充裕的片内存储(Memory bits),ALM的占用是FPGA中制约同步实现的主要因素。相比于传统二元加法器的互相关实现,PNACCS方法节约了近45%的ALM资源。相较于全三元加法器的实现,低位位宽P为7-9的PNACCS方法的ALM占用也减少了3%-6%。
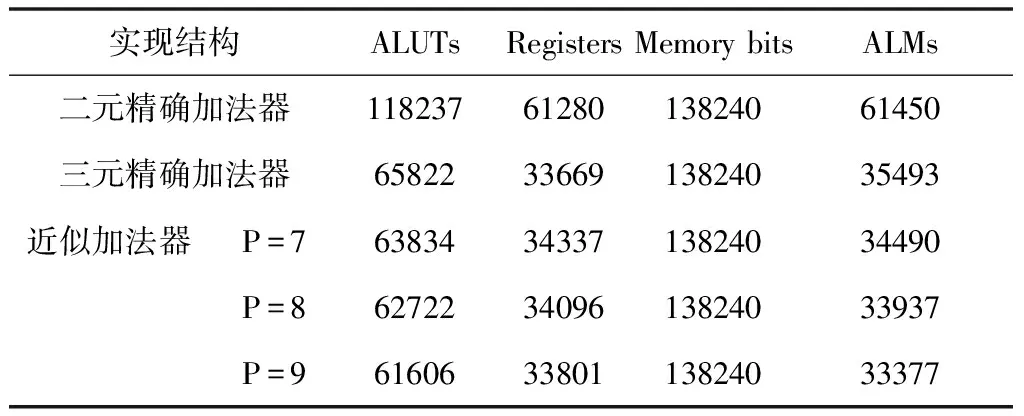
表1 不同加法器结构的互相关实现在FPGA中的资源占用情况
5 结语
本文针对传统互相关同步方法实现复杂度高的问题,提出了一种基于近似加法器的互相关同步改进方法。根据接收信号的统计特性和近似加法器原理,设计了一种改进的互相关结构;并对改进方法的同步性能和实现复杂度进行了分析。通过matlab平台对改进方法的时频同步性能进行了仿真,通过Quartus II和FPGA平台对改进方法进行了实现验证。仿真和实现结果与理论分析相一致:与传统的互相关方法相比,改进方法以较小同步性能的损失为代价;大大降低了实现的复杂度。所提方法有效弥补了传统互相关同步实现复杂度高的缺点,适用于各种需要精确同步的低信噪比无线通信系统,有良好的工程应用价值。

