低速风洞阵风发生器实验研究与分析

屈晓力，刘琴，朱 博，聂旭涛，王 超

1.中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000 2.中国空气动力研究与发展中心 设备设计与测试技术研究所，四川 绵阳 621000

0 引言

飞行器的飞行安全性极易受到气象条件的影响。阵风作为最为频繁常见的气象条件，会改变飞行器的空速和气动角，导致飞行器所受的气动力及力矩发生变化，进而影响飞行器的飞行特性[1]。阵风环境会引起导弹的刚体运动及弹性振动，从而影响导弹的结构安全、电气设备的可靠性及命中精度[2]。大型水陆两栖飞机、低速长航无人机等由于展弦比增大、重量减轻，机翼对阵风载荷的敏感性增大。阵风载荷是该类飞行器结构设计或强度分析的依据，阵风动力响应分析尤为重要，对确保飞行安全具有重要意义[3-6]。

研究阵风载荷对飞行器结构带来的不利影响及解决措施，通常采用的方法是数值计算或阵风响应风洞试验。数值计算主要包括频域计算和时域计算。频域计算主要计算频域中若干离散频率的非定常气动力[7]，但频域计算很难考虑到非线性带来的影响；时域计算方法是在时域内直接模拟阵风响应的方法[8-10]。阵风响应风洞试验主要通过模型试验方法对阵风的影响进行测试，以及对阵风响应分析、阵风减缓控制技术进行验证。在飞机阵风载荷预测和阵风载荷试验需求的驱动下，阵风风洞试验技术得到了较快的发展，B-52、C-5A 等机型都曾在风洞中开展过阵风减缓试验研究[11-13]，国内也进行了相关的风洞试验[14-16]。

从20 世纪60年代开始，国外就开展了关于阵风发生器的大量试验工作[17]。Greenblatt[18]在试验段下游出口增配叶栅，通过改变叶栅角度调整试验段流量及阵风风速、幅度，实现试验段气流的非定常流动。Saddington 等[19]在试验段上游设计叶栅式的阵风发生装置，在试验段内形成了可靠可控正弦变化的横向速度分离。Grssiom 等[20]证实了叶片式阵风发生器能够在流场中引入二维扰动，且在测试截面保持相位一致。国内已有几座风洞配置了阵风发生器并投入使用。刘晓燕等[21]通过数值模拟对影响阵风强度及其分布形态的各种因素进行了分析，发现速度极值在叶片下游各截面具有相似的分布形态，且在小迎角范围内与叶片摆角极值保持线性关系。陈磊等[22]研发出以地面轨道、立柱、横梁为框架结构的阵风发生试验设备，研究了试验段风速16 m/s 以下、叶片下游8 倍弦长位置的垂直方向阵风极值及其均匀性。上述文献虽从不同的角度对阵风流场特性进行了研究分析，但对影响风速极值的参数研究还不够完整，系统性不强；国内风洞研究的阵风发生器，大多是从机械和控制的角度出发，鲜有从流动转换成工程模型进行研究。为此，本文以0.55 m×0.4 m低速风洞为实验平台，以叶片式阵风发生器为研究对象，对影响阵风流场风速极值的设计参数（叶片弦长、数目、间距）、运行参数（叶片摆幅和摆动频率、来流速度）进行了系统的实验研究工作，比较了各参数对风速极值的影响情况，以为其他类似阵风发生器的设计提供参考。

1 实验设备和实验件

1.1 实验设备简介

0.55 m×0.4 m 低速风洞是一座回流式低速风洞（见图1），流场品质好且具备声学测试功能。风洞配有开口和闭口两个试验段，最高风速分别为100 和130 m/s，截面尺寸均为0.55 m×0.40 m，风速额定功率为132 kW[23]。本项实验研究在该风洞闭口试验段开展。

图1 0.55 m×0.4 m 低速风洞Fig.1 0.55 m×0.4 m low speed wind tunnel

1.2 实验件

在距试验段入口1 m 处，有一个直径0.3 m 的观察窗，实验时将观察窗拆除，安装阵风发生器实验件。实验件（见图2）主要由叶片组件、曲柄摇臂机构和驱动电机等组成。实验时，通过驱动电机和曲柄摇臂机构实现叶片按近似正弦的规律摆动。

图2 阵风发生器实验件Fig.2 Gust generator test system

阵风发生器的核心部件为叶片，叶片翼型为NACA0018，固定展长550 mm，设计了3 种弦长（100、75 和50 mm），旋转轴线位于叶片的1/4 弦长处。叶片组可实现单叶片、双叶片和三叶片3 种构型。叶片摆动频率有5 种状态（4、6、9、12 和15 Hz）。叶片摆幅有4 种状态（8°、14°、22°和30°），通过更换曲柄实现。

2 阵风发生器流动简化理论

以相同构型、横向布置的双叶片构成的阵风发生器为例，分析其下游的速度特性。为简化分析阵风发生器叶片下游P点的速度，忽略试验段洞壁的影响，同时假设阵风发生器的流场为准稳态，如图3所示。试验段气流方向为X，高度方向为Y，宽度方向为Z，以此建立坐标系。1、2 为横向布置、Y方向间距2Y0的两个叶片。当叶片摆动时，两叶片的升力可以近似用1/4 弦长位置的线性段涡流环量 Γ1、 Γ2表示。图3 中r1和r2分别为P点与环量Γ1和Γ2的距离。

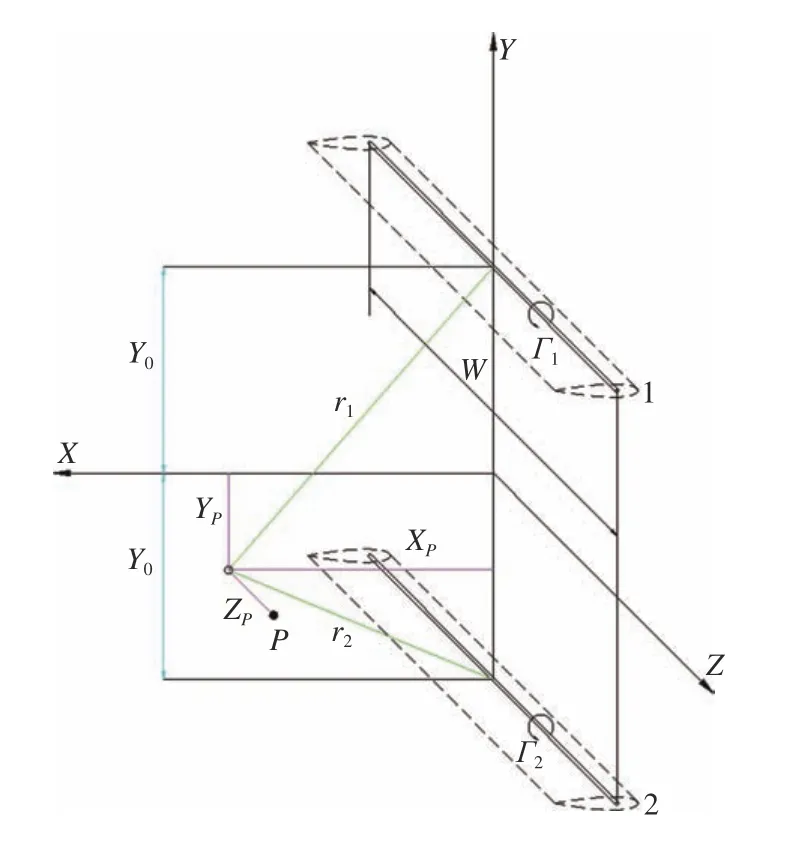
图3 阵风发生器下游流动简化模型Fig.3 Simple theoretical aerodynamic model of Gust generator

对于二维翼型，环量 Γ可用气流的轴向速度U、叶片的等效升力系数CLq和叶片弦长c表示：

若两个叶片均以相同的角速度 ω转动，且没有相位差，则并列的两个转动叶片等效升力系数Crq为：

上式中，k为奥多尔森系数，用于修正转动叶片升力系数与稳态叶片升力系数之间关系。

根据Biot-Savart 理论，叶片下游由环量产生的诱导速度 dV可表示为：

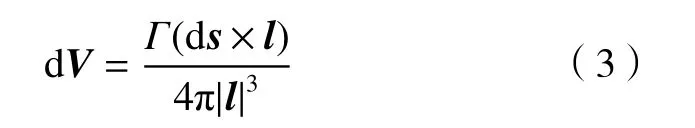
式中，ds代表翼型上的一个微元，l表示微元到P点的距离，则由叶片在P点产生的诱导速度V可表示为：

则两个叶片在P点产生的Y方向诱导速度VY可表示为：

根据上式推导可得VY：

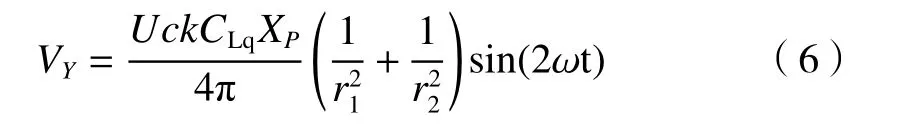
同理，当阵风发生器只有一个横向叶片时，其Y方向诱导速度VY为：

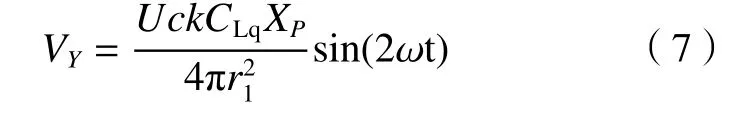
当阵风发生器有三个相同的横向叶片时，其Y方向诱导速度VY为：

由式（6）、（7）和（8），阵风发生器下游某点的Y方向诱导速度VY由来流速度（U）、叶片弦长（c）、奥多尔森系数（k）、叶片翼型升力系数（CLq）、该点在流场中的位置（XP、r1、r2、r3）和叶片角速度（ω）等共同决定。

3 实验方案及测试方法

3.1 实验方案

阵风响应风洞试验最关心的流场参数是阵风的风速极值VY，因此，本次实验的重点就是研究分析影响阵风风速极值的各种参数，并得到各参数与风速极值的具体影响关系。依据前文分析，实验参数分为2 组：第1 组为叶片设计参数（叶片弦长、数目、间距）；第2 组为叶片运行参数（风洞来流速度、叶片摆幅和摆动频率）。具体实验方案如下：

1）叶片设计参数影响实验：在同一叶片运行参数条件下，分别改变阵风发生器叶片弦长c、叶片间距2Y0，测量发生器后的阵风流场，研究不同叶片弦长、叶片数目、叶片间距对风速极值的影响情况。

2）叶片运行参数影响实验：在同一叶片设计参数条件下，分别改变来流速度U、调节叶片摆幅α、叶片摆动频率f，测量发生器后的阵风流场，研究不同叶片摆幅和摆动频率对风速极值的影响情况。

3.2 测试方法

实验所使用主要测试仪器为丹麦DANTEC 公司StreamLine CTA 多通道热线风速仪系统（图4），主要技术指标：频率响应⩽450 kHz，测速范围0.02～300.00 m/s。

图4 热线风速仪Fig.4 Hot wire anemometer

本次实验采用X 型二维热线探针（图5）来测量阵风流场的风速极值。实验时热线风速仪电桥频响设置为300 Hz，数据采样率1 kHz，采样时间5 s[18]。

图5 热线探针安装照片Fig.5 Photo of hot wire probe

阵风发生器下游Y向速度的测点位于试验段中心轴线上、距叶片尾缘300 mm。

4 实验结果与分析

4.1 叶片设计参数影响实验

图6 为在来流速度40 m/s、叶片摆幅8°、单叶片情况下，不同叶片弦长（50、75 和100 mm）对应的Y向阵风风速极值曲线。由图可知，不同叶片转动频率、不同弦长叶片下游的Y向速度极值增幅比例不一致。当叶片转动频率为9 Hz 时，Y向速度的增幅最大，当弦长由50 mm 增大到75 mm（增加50%弦长）时，Y向风速极值增大了0.14 m/s（增幅21%）；当弦长由50 mm 增大到100 mm（增加100% 弦长）时，Y向风速极值增大了0.32 m/s（增幅30%）。相同来流风速、相同叶片转动频率下，叶片弦长增大，翼型的雷诺数增大，相同迎角下的叶片升力系数理当略有增大，见式（7）。当叶片弦长增大50% 和100% 后，Y向风速极值的增幅应略大于50%和100%，但实测结果却为21%和30%，原因在于式（7）中的奥多尔森系数k是基于试验数据的经验值，对于不同弦长的叶片，该系数的修正量存在差异。

图6 不同叶片弦长时风速极值Fig.6 Wind speed amplitude for different blade chord lengths of the gust generator

多叶片的阵风发生器，其叶栅与单叶片的气动性能可能存在差异。为判断阵风发生器多个叶片之间可能出现的叶间干扰对叶片升力系数的影响，进行了不同叶间距三叶片下游Y向速度测试。由式（8）可知，当来流风速一定时，叶片间距增大，r随之增大，Y向速度应呈减小趋势。图7 为来流速度40 m/s，叶片摆幅8°，叶片弦长50 mm，叶片间距分别为50 mm（1.0c）、60 mm（1.2c）和70 mm（1.4c）情况下Y向风速极值的对比。叶片间距增大后，风速极值先增大后减小，当叶片间距为1.2c时，Y向风速极值最大。当叶片间距为1.0c（实度为1.00）时，叶间干扰将导致单叶片的升力与理论值存在较大差异，等效升力系

图7 不同叶片间距时风速极值Fig.7 Wind speed amplitude for different blade spacing of the gust generator

数的减小占比大于叶片间距对Y向风速极值的影响；当叶片间距大于1.2c时，随着叶片间距的增大，Y向风速极值减小，这表明当叶片间距大于1.2c（实度小于0.83）后，叶间干扰带来的等效升力系数减小对Y向风速极值的影响小于叶片间距的影响。叶片间距在此情况下对Y向风速极值的变化趋势起到决定性作用。

图8 为来流速度40 m/s、叶片摆幅8°、叶片弦长50 mm、叶片间距60 mm 情况下，叶片数目为1、2、3 时Y向风速极值的曲线。由图可知，随着叶片数目的增加，Y向风速极值呈增大趋势。当叶片转动频率不大于9 Hz 时，单叶片增加到双叶片对应的Y向风速极值增幅大于双叶片增加到三叶片对应的Y向风速极值增幅；当叶片转动频率为15 Hz 时，Y向风速极值与叶片数目呈线性关系。叶片转动频率为12 Hz时，Y向风速极值的增幅最大。当叶片由1 片增加到2 片（增加100%）时，Y向风速极值增加了0.44 m/s（增幅35%）；当叶片由2 片增加到3 片（增加50%）时，Y向风速极值增加了0.64 m/s（增幅38%）。Y向风

图8 不同叶片数目时风速极值Fig.8 Wind speed amplitude for different numbers of blades of the gust generator

速极值增幅明显小于叶片数目的增幅，其原因在于叶片增加后，流场更易受到洞壁的影响，导致实际的气流迎角小于理论迎角，进而造成升力系数的减小。

4.2 叶片运行参数影响实验

在固定叶片数量、间距的基础上，通过改变叶片摆幅α和摆动频率f（ω=2πf），对阵风发生器下游Y向风速极值变化进行研究。

由于机械设计原因，阵风发生器在风洞内运行时会出现机构振动以及动载荷等问题。在叶片电机功率固定情况下，叶片的摆幅与摆动频率无法同时达到最大值，实验时叶片摆幅8°对应的最大摆动频率为15 Hz，叶片摆幅30°对应的最大摆动频率为6 Hz。

图9 为来流速度40 m/s、三叶片、叶片间距60 mm、叶片弦长50 mm 情况下，Y向风速极值随摆动频率的变化曲线。由图可知，在叶片摆幅为8°时，摆动频率从4 Hz 提升至15 Hz，Y向风速极值由1.53 m/s 增大至2.64 m/s，增幅73%，且随着频率提升，Y向风速极值呈线性增长。在叶片摆幅为14°、22°和30°时，随着摆动频率的增大，Y向风速极值也呈线性增长。根据第2 节的分析，阵风发生器下游的Y向诱导风速与来流速度、叶片弦长、等效升力系数等成正比，在相同的风速、叶片构型和叶片摆幅条件下，增大叶片的摆动频率，实际上增大了垂直于叶片方向的气流速度，导致叶片升力增大。根据实测数据，风速增大与叶片频率的增大呈线性关系，由此推断，当阵风发生器的叶栅在一定的摆动幅度和摆动频率下，式（8）中的参数kCLq与频率f呈线性关系。

图9 不同摆动频率时风速极值Fig.9 Wind speed amplitude for different oscillation frequencies of the gust generator

图10 为来流风速40 m/s、三叶片、叶片间距60 mm、弦长50 mm 情况下，Y向风速极值随摆幅的变化曲线。由图可知，摆动频率为4 和6 Hz 时，随着摆幅的增大，Y向风速极值单调线性增大。这是因为在摆动频率与来流速度一致的情况下，摆幅的增大意味着叶片迎角的增大，在叶片失速前，迎角与叶片升力系数呈线性关系，式（8）中的参数kCLq与叶片摆幅成正比。由图10 还可得到，当叶片摆幅大于22°时，Y向风速极值随叶片摆幅变化曲线的斜率开始变缓，这可能是由于叶片摆幅较大，叶片表面的气流开始分离、等效升力增加变缓导致的。

图10 不同叶片摆幅时风速极值Fig.10 Wind speed amplitude for different blade amplitudes of the gust generator

图11 为三叶片、叶片间距60 mm、叶片弦长50 mm情况下，不同来流风速对Y向风速极值影响的对比（不同摆动频率对应的摆幅均为8°）。以叶片摆动频率为4 Hz 的试验结果为例，随着来流风速的增大，Y向风速极值呈增大趋势，来流风速为20、30 和40 m/s时（增幅分别为50% 和33%），Y向风速极值分别为1.00 、1.20 和1.53 m/s（增幅分别为20%和28%）。依据式（8），阵风发生器下游固定位置的Y向速度与来流风速应呈正比关系，而实测的Y向风速极值并未因来流风速增大而线性增长，这是由于来流速度的增大会减小叶片的迎角，叶片等效升力系数降低。

图11 不同来流速度下风速极值Fig.11 Wind speed amplitude for different freestream speed

此外，在实验过程中，即使叶片摆幅不大，但当叶片摆动频率超过15 Hz 时，阵风发生器结构振动达到了无法忽略的程度。若阵风发生器直接安装在洞体壁面，很可能引起风洞的不良振动及破坏。因此，阵风发生器应尽量设置独立基础，与风洞调整隔开。

5 结论

本文针对叶片式阵风发生器的运行特点，通过简化的定常涡升理论，推导出阵风发生器下游流场Y向风速的计算公式。通过实验较为系统地研究了阵风发生器的设计参数（叶片弦长、数目和间距）和运行参数（叶片摆幅和摆动频率、来流速度）等对阵风流场风速极值的影响，可为其他风洞的阵风发生器设计提供参考。

1）推导的简化公式能够解释阵风发生器各设计和运行参数变化后，其下游流场Y向风速的变化机制。

2）从增大阵风发生器下游流场Y向风速极值的角度出发，增加叶片数目比增加叶片弦长更能增大Y向速度；在只考虑Y向风速极值的情况下，在叶片失速前，增加叶片摆幅比增大叶片摆动频率更有效。

3）采用多组叶片的阵风发生器，叶片间距不能太小，否则会导致等效升力系数下降，当叶片间距为1.2 倍弦长时，能够获得最大的Y向风速极值。