三维楔体诱导高超声速层流分离油流显示实验研究
王军旗,陈 政,倪招勇,甘才俊,李烺
1.中国航天空气动力技术研究院,北京 100074;2.中国运载火箭技术研究院,北京 100076
0 引言
襟翼舵(Flap rudder)是高超声速飞行器常用的一种气动控制面,一般安装于飞行器尾部或突出于底部。当舵面偏转时,将导致激波/边界层干扰,并伴随局部流动分离现象,尤其是在层流边界层中更容易发生局部流动分离。对于此类压缩面诱导的流动分离现象,以往多注重二维特性研究[1-6],而对有限展宽的三维效应则关注较少。有关研究表明,高超声速层流分离对各种干扰因素更为敏感[7-8],可能会对气动特性带来很大影响。对高超声速层流分离问题进行数值模拟时发现[9-10],各种数值因素(格式、限制器、网格、熵修等)会对分离区的大小、结构产生明显影响,对于有效模拟局部层流分离现象,迄今尚未形成普适性的算法和模拟准则。同时,在模拟有层流分离的定常流动时,分离区的计算收敛时间远大于无流动分离时的情况[7]。因此,在数值模拟大范围层流分离流场时,采用定量描述分离流动结构的实验结果对数值方法进行检验是十分必要的。
油流显示技术是实验中描绘分离流动结构的有效手段,但在地面风洞设备中获得高超声速条件下的局部层流分离流动图谱还存在很大难度,主要是因为:大多数暂冲式高超声速风洞雷诺数较高,不易实现模型表面全层流状态;而脉冲式风洞由于有效实验时间太短,表面油流技术难以形成清晰的油流分离图谱[11]。在以往研究中,对高超声速层流分离区域主要是通过压力、摩阻或热流的测量结果加以判别[3,12-13],这只能大致界定分离点位置,难以形成对表面分离区域以及分离区内流动结构的直观认识。
本文采用两种模型(传统的矩形平板/三维楔体、三角形平板/三维楔体),在高超声速风洞Ma=6.0 条件下,开展三维楔体诱导层流分离流动的油流显示实验研究,以获得三维楔体诱导的层流分离图谱,研究前体外形对局部层流分离结构的影响。
1 实验模型和方法
1.1 实验设备
实验在中国航天空气动力技术研究院FD-03 风洞中开展。该风洞是一座暂冲、下吹、自由射流式常规高超声速风洞,喷管出口截面尺寸170 mm×170 mm,马赫数为5、6、7、9,总压范围为0.8~3.5 MPa,总温范围为358~1028 K,单位雷诺数为5.0×107~2.3×107/m。
1.2 实验模型
设计了适用于模拟三维楔体诱导流动分离特征的两种实验模型,第一种为传统的“矩形平板+三维楔体”模型(后文简称矩形平板模型),如图1所示;第二种为具有一定高超声速飞行器特征的“三角形平板+三维楔体”模型(后文简称三角形平板模型),如图2所示。两种模型使用相同的三维楔体,楔体安装于模型尾部,可拆装;通过更换不同角度的楔体改变楔角δ,楔角δ分别取5°、10°、15°和20°。

图1 矩形平板+三维楔体模型Fig.1 Rectangular flat plate with 3D wedge

图2 三角形平板+三维楔体模型Fig.2 Triangular flat plate with 3D wedge
实验前,以L=200 mm 的矩形平板(后部无三维楔体)进行摸底实验,初步判定距前缘150 mm 左右流场开始转捩。结合以往FD-03 风洞其他实验结果,确定正式实验模型长度为120 mm。图1 和2 中模型沿流向的几何尺寸L=120 mm,横向宽度H=80 mm,平板厚度t=10 mm。矩形平板采用15°的尖前缘,可使平板上表面流动尽量接近二维流动,能够与以往的二维实验结果进行对比。三角形平板则未采用尖前缘,主要目的是为了更近似于高超声速飞行器外形,实验结果可为高超声速飞行器外形设计提供借鉴。三角形平板头部为半径R=2.5 mm 的球冠,侧缘为半径2.5 mm 的柱面。图3 和4 分别为两种模型的照片。

图3 矩形平板模型照片Fig.3 Photo of rectangular model
1.3 实验条件
试验段来流条件为:马赫数Ma=6.0,总压p0=1.2~2.0 MPa,总温T0=470 K。对应的单位雷诺数Re范围为1.12×107~1.87×107/m(Re=ρ∞u∞/µ∞,ρ∞、u∞和 µ∞分别为来流密度、速度和动力黏性系数)。相应地,由模型长度定义的最大当地雷诺数ReL为1.34×106~2.24×106(ReL=ρ∞u∞L/µ∞)。
实验过程中,通过安装于模型上方的摄像设备以及电脑视频采集卡连续采集图像,并适时判定流场是否达到稳定状态。

图4 三角形平板模型照片Fig.4 Photo of triangular model
1.4 油流实验方法
油流法是一种经典的流动显示方法,它是一种非常简便、有效的显示分离流动的流体力学实验技术。针对高超声速流动特点,选用二氧化钛粉末和油剂配制为混合试剂,模型在风洞试验台上安装完成后、风洞启动前,将调制好的混合试剂均匀涂抹于模型表面。风洞启动后,通过安装于模型上方的摄像设备连续记录模型表面油流图谱视频,直至图像显示的流动结构稳定无变化时停止实验。
若试剂过稠,则粒子跟随性较差,需较长实验时间才有可能形成稳定的流动结构(有时甚至无法形成清晰的图谱);若试剂过稀,在尚未形成稳定的流动结构前,试剂就会流失殆尽。因此,在正式实验前,一般需先进行若干次预备性探索实验,通过适当调整试剂组分比例,获得较高清晰度的流动结构显示结果。
1.5 层流状态的确认
首先进行了矩形平板模型的层流状态确认实验。模型采用如图5 和6所示的两种安装方式。对于第一种安装方式(图5),矩形平板前缘与风洞喷管出口下壁面平齐,由于喷管下壁面边界层为已充分发展的湍流,模型表面应为全湍流状态,三维楔体只可能形成湍流分离;对于第二种安装方式(图6),模型远离喷管壁面边界层,模型上表面初始段应为层流状态,当流动到达三维楔体处,通过对比不同条件下的实验结果,并结合数值模拟结果,对分离流态进行确认。

图5 模型安装方式一(来流为湍流)Fig.5 Installing type Ⅰ(turbulent inflow)
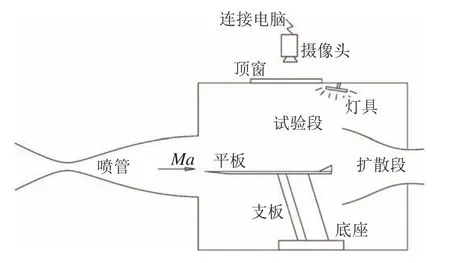
图6 模型安装方式二(来流为层流)Fig.6 Installing type Ⅱ(laminar inflow)
图7 和图8 分别为20°楔角、p0=2.0 MPa(Re=1.49×107/m)条件下采用两种模型安装方式获得的油流图谱。对于模型安装方式一,由于来流为充分发展的湍流,分离范围非常小(相当于刚刚发生分离),这与Holden[2]关于二维压缩拐角在湍流情况下的初始分离角为20°的结论基本一致。对于模型安装方式二,可以看到分离区远大于图7所示的湍流分离,因此可以初步判定图8 为层流分离状态。为进一步说明这一结论,将来流总压降低至1.6 MPa(相当于降低雷诺数为1.22×107/m),发现油流图谱基本与图8一致,即降低来流雷诺数之后,分离区未发生明显的变化。

图7 模型安装方式一的油流图谱Fig.7 Oil flow pattern obtained from type Ⅰ(turbulent)

图8 模型安装方式二的油流图谱Fig.8 Oil flow pattern obtained from type Ⅱ(laminar)
此外,对流场进行了数值模拟。采用三维可压缩Navier-Stokes 方程作为控制方程,通过有限体积方法进行离散,对流项离散采用Roe 格式,通过MUSCL 插值达到二阶精度,黏性项离散采用中心差分格式,时间项离散为隐式LU-SGS 方法,进行稳态流场计算。
图9 为采用SA 湍流模型获得的数值模拟结果,图10 为层流数值模拟结果。采用湍流模拟得到的结果与图7 的实验结果基本一致,采用层流模拟得到的结果与图8 的实验结果也基本一致。基于此,可以进一步确定图8 给出的油流分离图谱为层流分离,因此,在来流总压小于2.0 MPa 时,可以保证L=120 mm的矩形平板模型表面为全层流状态。

图9 湍流数值模拟结果Fig.9 The streamlines by turbulence numerical simulation

图10 层流数值模拟结果Fig.10 The streamlines by laminar numerical simulation
2 实验结果及分析
如图11所示,为定量分析流动分离结构的特性,将实验获得的油流图谱与模型表面敷贴坐标纸

图11 分离流动结构标定及分离距离Ls 的定义Fig.11 Coordinate calibration of separation structure and definition of separation distance(Ls)
的照片叠合,定义分离线与平板中心线的交点为最远分离点,定义该点至楔体前缘的距离为分离距离,以Ls表示。
2.1 实验结果的重复性
在给定实验条件下,两种模型均可获得稳定的分离流动状态。图12 给出了矩形平板模型20°楔角、相同来流条件下两个车次的表面分离流动对比,图13为三角形平板模型在相同条件下的两个车次对比,可见实验结果的重复性都比较好。通过对实验视频的分析,也发现流动分离现象都比较稳定。

图12 矩形平板模型两个车次的实验结果重复性比较Fig.12 Repeatability of experimental results from two runs for rectangular model

图13 三角形平板模型两个车次的实验结果重复性比较Fig.13 Repeatability of experimental results from two runs for rectangular model
2.2 矩形平板模型实验结果
以第二种安装方式(图6)将矩形平板模型安装于FD-03 高超声速风洞中。实验参数为:Ma=6.0,p0=2.0 MPa,T0=470 K,单位雷诺数为1.87×107/m。
图14 为三种楔角(δ为5°、10°和20°)条件下的油流图谱。以坐标纸标定的分离距离Ls分别为2、8 和21 mm,以模型长度L进行无量纲化(L′=Ls/L),对应的无量纲分离距离L′分别为0.017、0.067 和0.175。由此可见,随着楔角δ的增大,分离范围相应增大,但分离线形态基本无变化。

图14 矩形平板模型不同楔角的油流图谱Fig.14 Oil flow patterns with three compression angles for rectangular model
楔角δ=5°时,仍然存在小的分离区,说明在此来流条件下,初始分离角小于5°,这与一般认为高超声速二维楔体层流分离初始分离角在10°左右的结论[3]并不一致。对二维楔体流动分离的判定,以往是基于压力或热流等测量结果进行的;对于极小的分离区域,由于在楔体根部无法布置足够密集的测点,以有限的测点难以识别流动分离现象,这也是油流实验判定流动分离相较于压力测量的优势所在。
2.3 三角形平板模型实验结果
现代高超声速巡航飞行器一般采用面对称的升力体外形,机身下表面曲率小,比较扁平。当安装于后体的襟翼舵偏转时,虽然在一定程度上类似于平板/楔体的激波/边界层干扰问题,但襟翼舵宽度有限,边缘激波弱化,且受到前体外形影响,激波/边界层干扰可能导致更为复杂的三维流动结构。
本文采用如图3所示的简化三角形平板模型,具有一定的高超声速飞行器外形特征。模型安装方式如图6所示(迎角为0°和10°)。选择实验参数时,采用了比矩形平板模型更小的来流总压(几乎达到FD-03 风洞正常启动的最低总压),目的是实现更小的雷诺数。具体参数为:Ma=6.0,p0=1.36 MPa,T0=470 K,对应的单位雷诺数Re=1.27×107/m。
图15 为0°迎角、三种楔角(10°、15°和20°)条件下的油流图谱。在三角形前体外形的影响下,分离线呈“m”状,与矩形平板模型上的分离形式有明显区别,三维效应更加显著。定义“m”分离线最上游的点到楔体前缘的距离为分离距离Ls,则三种楔角下Ls分别为8、13 和17 mm,对应的无量纲分离距离L′分别为0.067、0.108 和0.142,说明分离范围随楔角δ的增大而增大。楔角δ=5°时,未发现流动分离,此处未给出油流图谱。

图15 三角形平板模型不同楔角的油流图谱(α=0°)Fig.15 Oil flow patterns with three compression angles for triangular model(α=0°)
图16 为10°迎角、不同楔角条件下的油流图谱。此时的分离形式不但与矩形平板模型不同,与相同模型0°迎角的情况区别也很大。分离区呈狭长形,向上游推进了更远距离。表1 为不同实验条件下的分离距离对比,在同样的20°楔角条件下,矩形平板模型上的最大分离距离Ls为21 mm(L′=0.175),而三角形平板模型0°迎角时的Ls为17 mm,10°迎角时Ls为44 mm,L′分别为0.142、0.367,表明三角形平板模型在有迎角情况下,分离距离明显大于无迎角的三角形平板模型和矩形平板模型;同时,对于三角形平板模型,10°迎角下的分离形式与0°迎角差别很大,说明对于三角形前体上的流动分离范围和分离形式,迎角也是一个重要影响因素。

图16 三角形平板模型不同楔角的油流图谱(α=10°)Fig.16 Oil flow patterns with two compression angles for triangular model(α=10°)

表1 不同实验条件下的无量纲分离距离L′对比Table 1 Comparison of dimensionless separation distance L´
当高超声速流动被三维楔体阻挡,楔体前产生斜激波,造成表面的逆压梯度。楔角越大,激波越强,逆压梯度越大,分离范围也越大;楔体侧面逆压梯度小,分离点后移,分离线总体为包围楔体的结构。对于矩形平板模型,表面流动几乎为二维均匀流,分离线三维弧形结构主要由楔体三维性质导致;对于三角形平板模型,未分离的表面流动已存在明显三维流动特征,流动更易发生转捩。因此,本文的三角形平板模型采用比矩形平板模型更低的实验压力才能保持层流状态,且呈现出更加复杂的三维流动分离结构,迎角变化对分离结构也产生了显著影响。
对于实际有襟翼舵的高超声速飞行器,机身表面一般不是平面,前体曲面外形与后部襟翼舵的相互影响将导致更加复杂的层流分离形式[14],因此,应当针对具体的飞行器外形研究其层流分离特性,并评估大范围分离对气动力/热特性可能产生的影响。
3 结论
开展了三维楔体诱导高超声速层流分离油流显示实验研究,获得了两种不同前体外形上三维楔体诱导的层流分离油流图谱。结果表明:随着楔角增大,分离范围增大。前体外形是楔体诱导层流分离形态的重要影响因素之一,对于三角形前体,分离流动的三维效应更加显著,不同迎角下的层流分离形态也有明显区别。因此,对于采用襟翼舵进行飞行控制的实际高超声速飞行器,需要结合具体的前体外形,针对性地研究襟翼舵诱导的层流分离特性。

