一种新的鲁棒PM滤波及其在组合导航中的应用*

梁 浩 张子剑 贾 睿 崔利军

1.北京宇航系统工程研究所，北京 100076 2.太原卫星发射中心，山西太原 030027

0 引言

星光导航系统(CNS)具有精度高、自主隐蔽的特点，能够为载体提供高精度姿态信息[1]；合成孔径雷达(Synthetic Aperture Radar，SAR)是一种高精度微波成像雷达，它具有全天时、全天候、远距离工作的优点[2]；CNS、SAR和捷联惯导(SINS)组成的CNS/SAR/SINS组合导航系统是一种性能优异的无依托自主导航方式[3-4]。

Kalman滤波限制条件比较苛刻，要求系统模型精确已知，然而在实际应用中，受各种条件的限制，很难获得噪声准确的先验统计特性；另一方面，系统的噪声特性也是不稳定的，噪声特性因内部器件特性变化或外部力学冲击等环境因素，可能产生不可预知的变化。

为了处理这种存在偏差的系统，鲁棒滤波被研究并发展应用起来，M估计滤波和H∞滤波是2种最典型的鲁棒滤波，被广泛用来处理高斯分布受到污染或干扰的系统。M估计滤波对应用系统的噪声特性变化较迟钝，能够解决系统噪声和测量噪声统计特性不确定的问题[5-6]，H∞估计滤波将模型误差看作未知但有界的噪声，使噪声污染情况下的估计误差最小[7]，但当系统出现尖锐的野值时，M估计滤波和H∞滤波均会出现较大误差以至发散。

本文针对组合导航系统中出现多种尖锐野值的情况，引入GM估计野值检测抑制方法，构建了鲁棒PM估计滤波，应用于高空飞行器CNS/SAR/SINS组合导航中，并进行了仿真分析。

1 基于M估计的线性滤波

1964年，Huber经过严格的推导[5]，提出了广义极大似然估计，即M估计鲁棒滤波。针对高斯噪声受到污染的系统，M估计结合了l1和l2范数构造代价函数，其鲁棒性优于l2范数估计，其优点是保证最大渐近估计方差最小以及纯高斯分布时l2范数估计的效率。

线性离散系统如下

xk=Fk-1xk-1+wk-1

(1)

yk=Hkxk+vk

(2)

式中：xk为状态量，yk为观测量，Fk-1为状态转移矩阵；系统噪声wk-1和量测噪声vk为高斯白噪声，方差为Qk-1和Rk。

1)预测

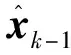
(3)

(4)

2)更新

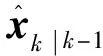
(5)

针对量测更新过程，构造线性回归模型以提高系统的冗余性：

(6)

定义如下变量：

(7)

(8)

(9)

(10)

则线性回归模型可以转化为

zk=Mkxk+ξk

(11)

M估计求解如下代价函数的极小值，通过求解代价函数获得状态估计值：

(12)

式中：ei=(zk-Mkxk)i；ρ为任意函数，通过选择ρ函数，可以使估计器获得某些特定的性质，Huber建议的ρ函数形式如下

(13)

式中：μ为可调节参数。而当残差较大时，ρ函数具有l1范数的性质，相反当残差较小时，ρ函数具有l2范数的性质。通过配置μ，可以使滤波器在高斯分布下具有较高的估计效率，并且能够抑制滤波噪声污染对系统的影响。

Huber在公开文献中已证明，当选择式(13)作为ρ函数的形式时，M估计滤波对受污染的高斯系统具有渐近最优鲁棒性。

2 鲁棒PM估计

2.1 系统野值的类别及影响

在实际系统中除了存在受污染的高斯噪声，还会存在各种干扰野值，一般认为在组合导航系统中出现的野值主要是系统状态野值和量测野值2种，然而状态转移矩阵和量测矩阵中也会出现野值，称为结构野值，结构野值是由时变系统模型匹配错误和计算浮点数错误等引起的，3种类型野值列表如下。

在回归模型中野值点远离其它正常点，会对M估计产生较大的影响，M估计也仅能够抑制系统的部分量测野值，当系统同时存在表1中的3种野值时，M估计滤波会出现偏差。

表1 组合导航系统中3种野值类型

近年来，在电力系统状态估计中，出现了一种广义M估计(GM估计)滤波算法[8]，通过构造回归模型并采用迭代方法求解最优估计，GM估计对量测野值、状态野值和结构野值均具有鲁棒性。GM估计包括Mallows型GM估计和Schweppe型GM估计2种，Mallows型GM估计在目标函数中引入权函数以降低所有量测点的权重，Schweppe型GM估计只针对野值点进行衰减，后者具有更高的效率。

2.2 GM估计中的PS野值检测方法

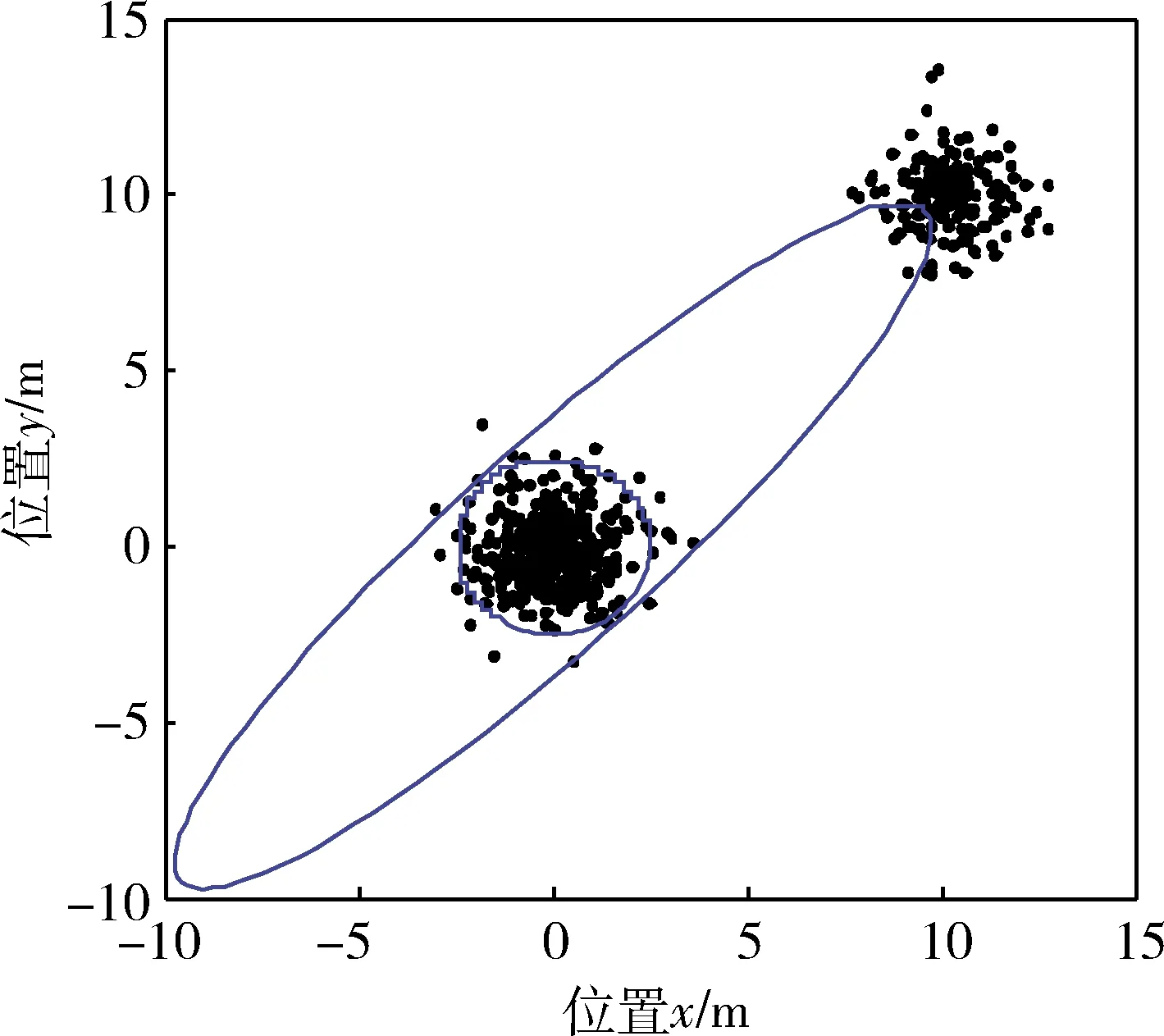
图1 导航系统中被污染的样本点

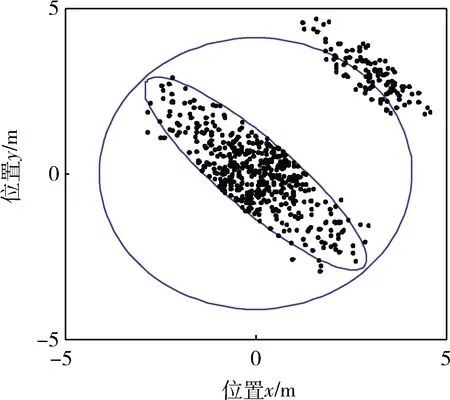
图2 预白化处理后的样本点分布

MD(Mahalanobis Distances)是一种经典的基于样本点均值和方差的野值检测方法，定义样本点集的中心为c=[p1,p2]T，同一组状态信息样本点形成一拟合圆，令di=[di1,di2]T表示样本点xi(i=1,…,m)到拟合圆的矢量，xi到拟合圆的距离为p3，那么di又可表示为di=(xi-c)(1-p3/‖xi-c‖)。MD野值检测方法表示如下

(14)

(15)

(16)

为此，人们提出了一种鲁棒的野值检测方法，鲁棒PS(Projection Statistics)检测法[9]，PS利用样本点中值和中值绝对偏差(Median Absolute Deviation, MAD)来构造检测方程：

(17)

式中：uk表示PSi检测的基准方向，每个点都需对m个方向的投影进行检测；PS方法受野值点干扰较小，当同时存在多处野值时也能够准定位，其计算速度也较快。

2.3 鲁棒PM估计滤波构建

将GM估计中的PS野值检测方法应用到M估计滤波中，构建一种新的鲁棒PM(Projection M-estimation)估计滤波。构建方法为：

(18)

3 CNS/SAR/SINS组合导航模型

3.1 捷联惯导误差传播模型

捷联惯性导航系统是飞行器CNS/SAR/SINS组合导航系统的核心，SINS的误差传播方程也是组合滤波器模型的基础。根据SINS误差传播方程构建组合系统的状态方程，利用CNS和SAR的外部导航量构建量测方程，设计滤波器对惯导误差进行估计。

以东北天地理坐标系为导航坐标系，CNS/SAR/SINS组合导航系统的惯导误差传播模型为[10-11]：

(19)

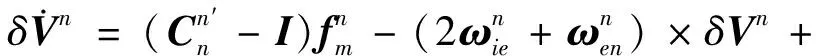
(20)

(21)

(22)

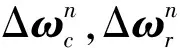
3.2 观测方程

星光导航系统中星敏感器实际测得的星光矢量可表示为

(23)

星光矢量的理论测量值为：

(24)

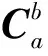
星敏感器对星光矢量的实际测量值rb与理论测量值pb有一定的偏差：

(25)

星光导航系统中一般将2个星敏仪正交安装，把星敏感器实际测得的2个星光矢量rb1、rb2与理论测量值pb1，pb2相减，得到CNS/SINS的观测量，INS的水平位置与SAR输出的水平位置之差构成SAR/SINS量测信息[12]，则CNS/SAR/SINS系统的量测方程为

(26)

其中：vk为量测噪声。

3 仿真校验

将常规Kalman滤波、M估计线性滤波以及鲁棒PM滤波分别应用于CNS/SAR/SINS组合导航系统进行数学仿真实验。

仿真参数设置为：飞行器初始位置为东经116°，北纬38°，速度180m/s，方位角40°，俯仰和滚转角为0°，飞行器有0.3m/s2的加速度和0.2(°)/s的转弯角速度。捷联惯导陀螺零漂不稳定值0.05(°)/h，加表零偏不稳定值100μg；星敏感器导航精度为20″(1σ)，SAR导航位置精度为20m(1σ)。仿真时间100s。

由于高空飞行器导航系统长时间工作，导航系统不可避免会出现各种野值、噪声特性产生变化。下面通过设置不同的仿真条件，对3种线性滤波算法进行对比分析。

仿真条件1：

各导航设备的噪声统计特性为受到污染的混合高斯分布，方差是原高斯分布的3倍，污染率为ε=0.2，混合高斯分布描述如下

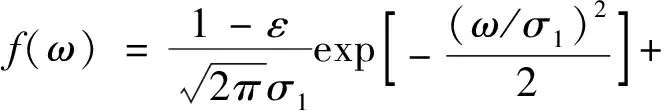
(33)

图4 水平位置估计总误差

仿真条件2：

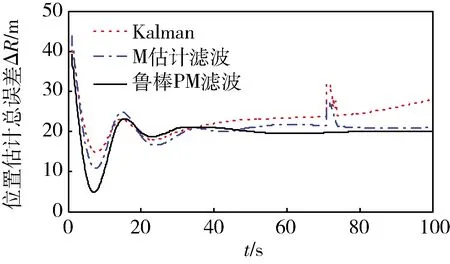
图6 水平位置估计总误差

仿真结果图3～4表明，当导航设备的噪声特性为混合高斯分布时，常规Kalman滤波呈发散趋势、估计误差较大，M估计滤波和鲁棒PM滤波估计精度较高，验证了M估计滤波和鲁棒PM滤波对受污染的高斯分布噪声具有鲁棒性。

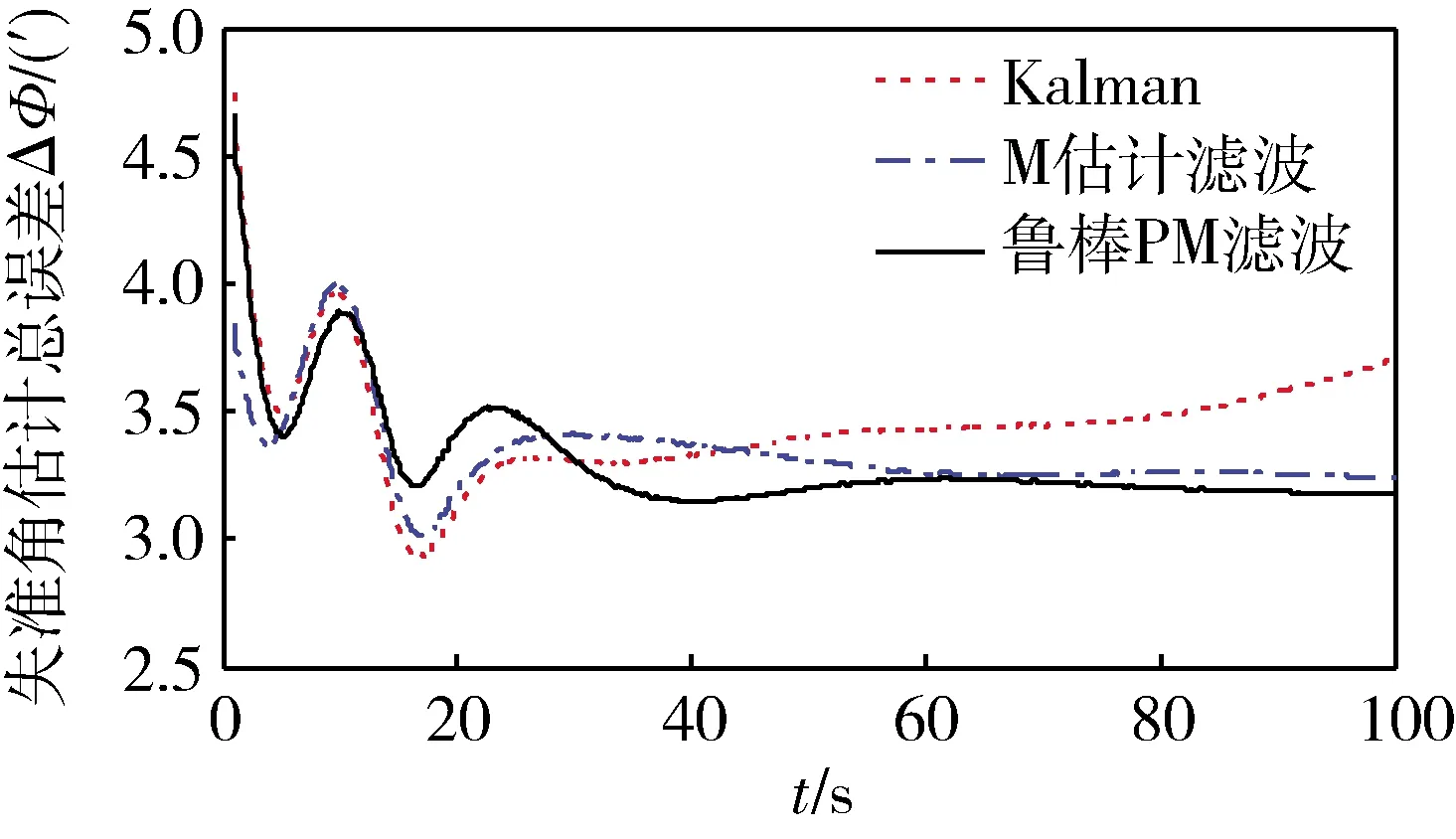
图3 三向姿态失准角估计总误差

仿真结果图5～6表明，当导航系统中存在尖锐野值和结构野值时，常规Kalman滤波和M估计滤波对这些野值无法抑制，而本文提出的鲁棒PM滤波使用了PS野值检测方法和鲁棒构架，可以对污染噪声和多种野值进行有效抑制。

图5 三向姿态失准角估计总误差

4 结论

分析了传统的M估计滤波在处理系统野值上的缺陷，借鉴了电力系统中的鲁棒PS野值检测方法，将鲁棒PM估计滤波应用到组合导航系统中，以CNS/SAR/SINS非线性组合导航为应用背景，对常规Kalman滤波、M估计线性滤波以及鲁棒PM滤波进行了对比分析。仿真结果表明，鲁棒PM滤波能够同时对受污染的高斯噪声和多种系统野值进行抑制，具有较强的结构抗差能力。