低频输电技术原理之一——M3C 的数学模型与等效电路

徐 政，张哲任

（浙江大学 电气工程学院，杭州 310027）

0 引言

随着海上风电开发向深远海方向发展，近年来海上低频输电技术越来越受到学术界和工业界的关注。对于海底电缆，采用低频输电方案的根本优势是可以降低电缆的并联电容效应，从而可以扩展海上交流输电的距离。比如，对于220 kV电压等级，工频50 Hz 下的合理输电距离大约为80 km[1]，如果海上风电场的离岸距离超过80 km，那么可选的输电方案主要是2 种，一种是直流输电方案，另一种就是低频输电方案。由于直流输电在换流站成本以及构网后的故障开断方面还存在不足，因此低频输电在远海风电送出以及海上风电场构网方面具有竞争优势。

采用低频方案进行远距离海底电缆输电的设想已有相当长的历史，至少1950 年在论证瑞典本土到哥特兰岛的输电方案（输电距离100 km）时已进行过技术经济比较[2-3]。当时比较了25 Hz，和直流3 种方案，最终还是采用了直流输电方案。陆上采用低频方案进行远距离大容量架空线路输电的设想是由王锡凡院士在1994 年提出的[4-5]，同样，陆上低频输电方案的主要竞争对手也是直流输电方案。近年来随着电力电子技术的发展，特别是MMC（模块化多电平换流器）技术的发展，低频输电技术已进入到了一个新的发展阶段，其在能源转型和构建新型电力系统方面有可能发挥重要作用。

低频输电方案的一个关键环节是低频系统与工频系统之间的接口，完成此功能的设备被称为变频器。实现变频器的电路拓扑有多种，其中一种具有良好工程应用前景的拓扑结构是M3C（模块化多电平矩阵变流器）。M3C 是在2001 年提出的[6-7]，跟MMC 为同一年提出[8]。经过20 年来的研究和改进，M3C 的理论已趋于成熟，其主要应用在电机调速领域，在高电压大容量输电领域还没有得到实际工程应用。

为了将M3C 应用于高电压大容量输电领域，需要解决主回路参数设计、过电压与绝缘配合设计、控制器设计以及设备制造等多方面的技术问题，以往文献对M3C 的数学建模和控制策略已有较多研究[9-13]，但对主回路参数设计、过电压与绝缘配合设计以及控制保护系统设计等涉及较少。本系列文章的目的是系统总结以往文献和本研究团队在M3C 数学建模和控制策略等方面已取得的成果，用一种便于理解且步步可追溯的方式将数学建模、主回路参数设计以及控制器设计的具体过程完整展示出来。期望本系列文章能对理解M3C 的运行原理有所帮助。

1 M3C 标准结构和变量命名

恰当的主回路结构展示形式和变量命名对于学习和应用M3C 技术是十分重要的。对于已接触过MMC 技术的读者，采用如图1 所示的M3C 主回路结构展示形式，而不采用原始的模块化多电平矩阵形主回路结构形式是更适合的。因为采用如图1 所示的M3C 主回路结构展示形式，就可以把M3C 看作是MMC 拓扑结构的扩展，而不是一个完全陌生的电路。图1 中的M3C 主回路结构，可以看作是在MMC 的上、下各3 个桥臂结构基础上又增加了中间3 个桥臂；进而使MMC 的从上桥臂公共母线到下桥臂公共母线之间输出直流电压变成了M3C 的从上桥臂公共母线、中间桥臂公共母线和下桥臂公共母线输出三相交流电压；进而达到了从输入端三相交流电压到输出端三相交流电压的变换，且这个变换包含了三相电压幅值的变换和三相电压频率的变换；进而达到了交-交变频器的功能。

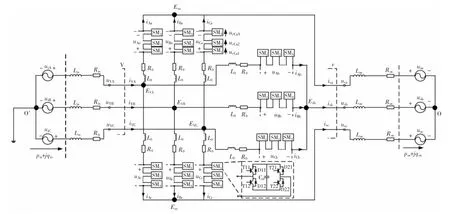
图1 M3C 拓扑结构示意

对于如图1 所示的三相M3C 拓扑结构，输入侧电气量的下标用大写字母（A，B，C）和字母i表示，输出侧电气量的下标用小写字母（a，b，c）和字母o 表示，桥臂电抗器和桥臂子模块的命名规则采用普遍接受的命名规则[14]，例如，uCa表示桥臂Ca 上所有子模块合成的电压，而ucCa1表示桥臂Ca 上第1 子模块的电容电压。需要特别注意：“V”和“v”是表示位置的符号，“V”表示输入侧的阀侧，“v”表示输出侧的阀侧，而“EVA，EVB，EVC”表示输入侧各相3 个桥臂的公共联接点，而“Eva，Evb，Evc”表示输出侧各相3 个桥臂的公共联接点。

2 M3C 的基本数学模型推导

2.1 abc 三相坐标系中的数学模型

根据基尔霍夫电压定律，可以得到M3C 微分方程数学模型：

将上面9 个方程从上到下按行排列成3×3 的矩阵形式，有：

同时，根据基尔霍夫电流定律，M3C 输入侧交流电流与桥臂电流之间的关系为：

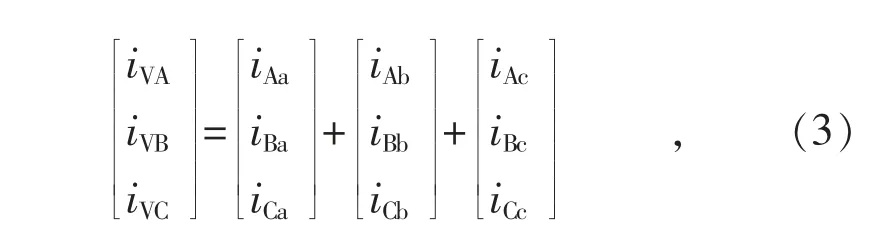
M3C 输出侧交流电流与桥臂电流之间的关系为：

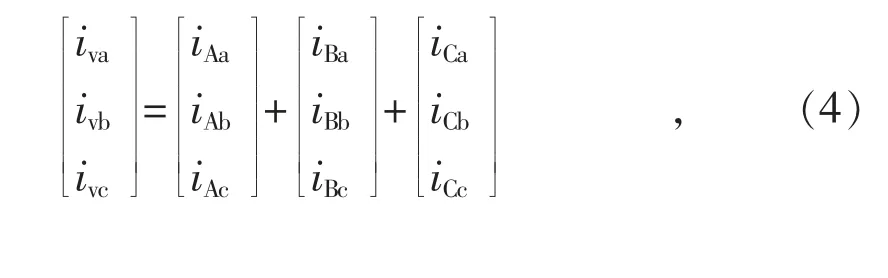
定义输入侧共模电压：

定义输出侧共模电压：

2.2 αβ0 正交坐标系中的数学模型

由于abc 三相物理量可以看作是一个旋转空间向量在abc 3 个静止坐标轴上的投影，但abc 3个静止坐标轴互差120°，不是一个正交坐标系，因而在abc 三相坐标系中不可能做到三相物理量之间的相互解耦。而对于M3C 的分析计算和控制器设计，在各坐标轴物理量相互解耦的坐标系中实施一定是更加简便的。正交坐标系天然就有各坐标轴上物理量相互解耦的特性，因而就自然想到用正交坐标系来代替abc 坐标系，然后基于正交坐标系中的物理量进行计算的思路。这种思路早已被想到，最著名并被广泛应用的正交坐标系就是αβ0 坐标系，而从abc 坐标系到αβ0 坐标系的变换矩阵被称为Clarke 变换[15]。利用正交坐标系进行分析的另一个优势是可以使描述数学模型的方程数目减少。在正交坐标系中，只有相互独立的数学方程会被呈现出来，不独立的冗余方程自然地会被消去。例如，对于abc 三相对称系统，三相电压和三相电流的零序分量等于零，这样将三相电压和三相电流变换到αβ0 正交坐标系中后，只有描述α 轴和β 轴物理量的方程是有意义的，0 轴上的方程是冗余方程，自然地就消失了，这样就将描述abc 三相物理量的3 个方程减少成为2 个方程。以下推导M3C 在αβ0 坐标系中的数学模型。

定义abc 到αβ0 的变换矩阵Tabc-αβ0为[16]：

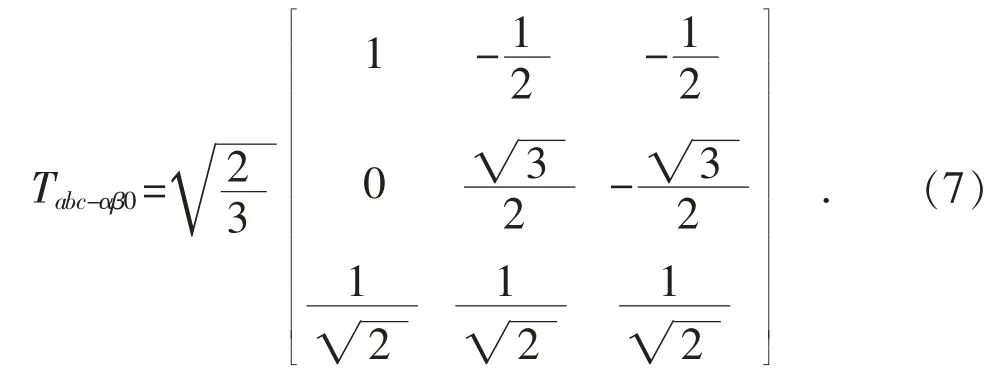
对应地从αβ0 到abc 的变换矩阵Tαβ0-abc为：

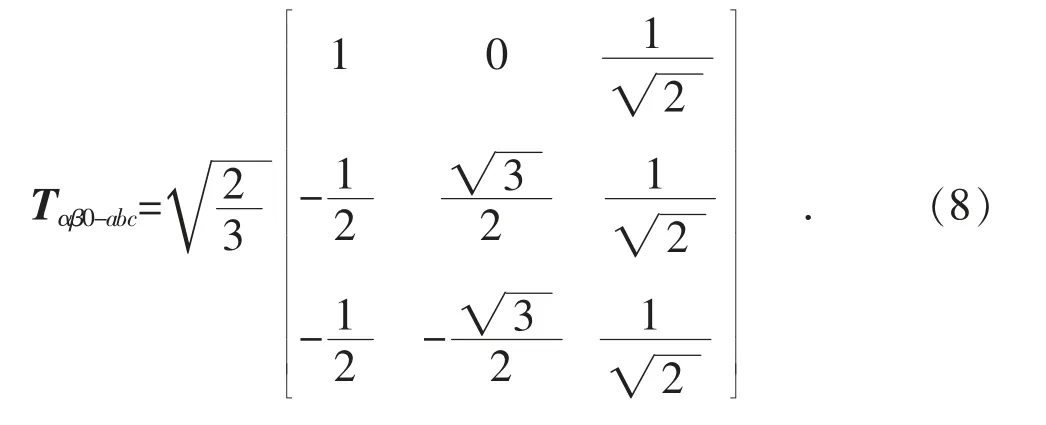
注意Tabc-αβ0和Tαβ0-abc为正交矩阵，（Tabc-αβ0）-1=（Tαβ0-abc）T。

将输入侧ABC 坐标系中的各变量变换到αβ0 坐标系，其变换式如下，注意矩阵表达式可以按列分开理解。

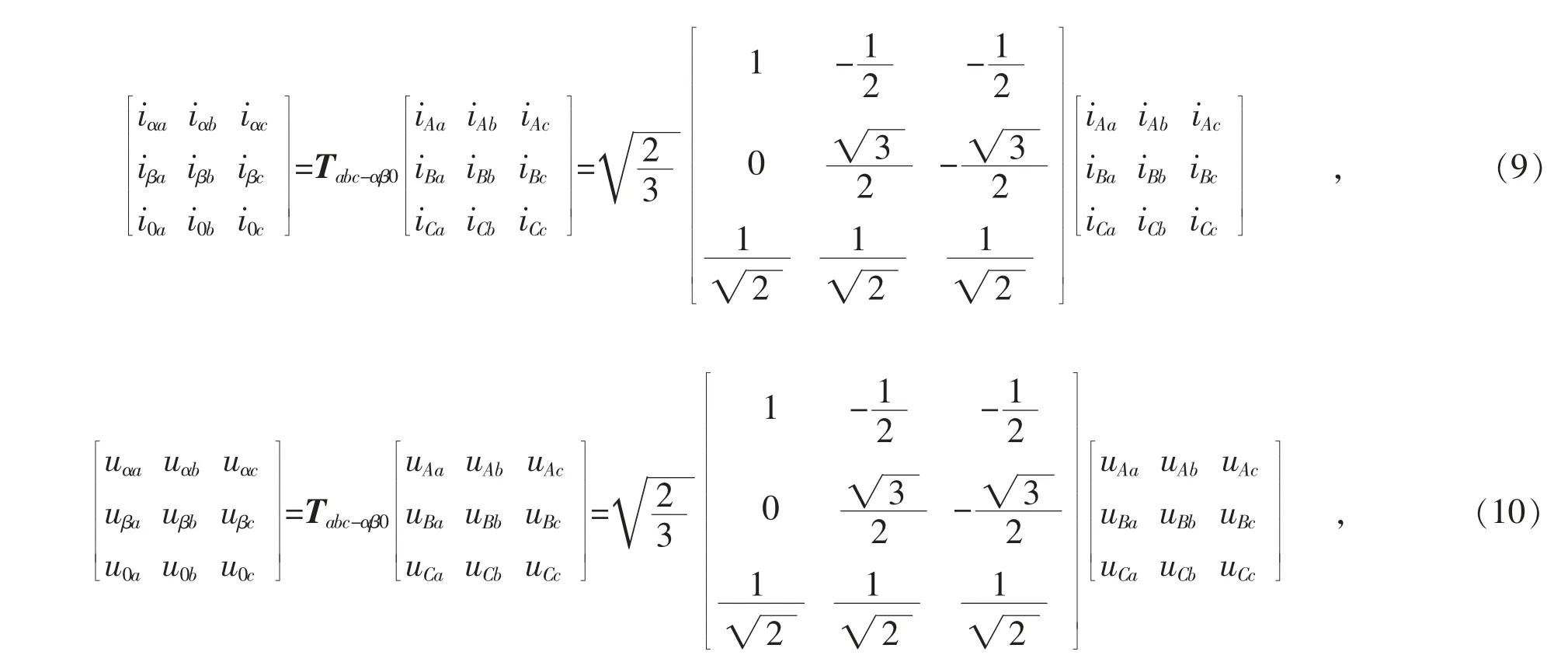
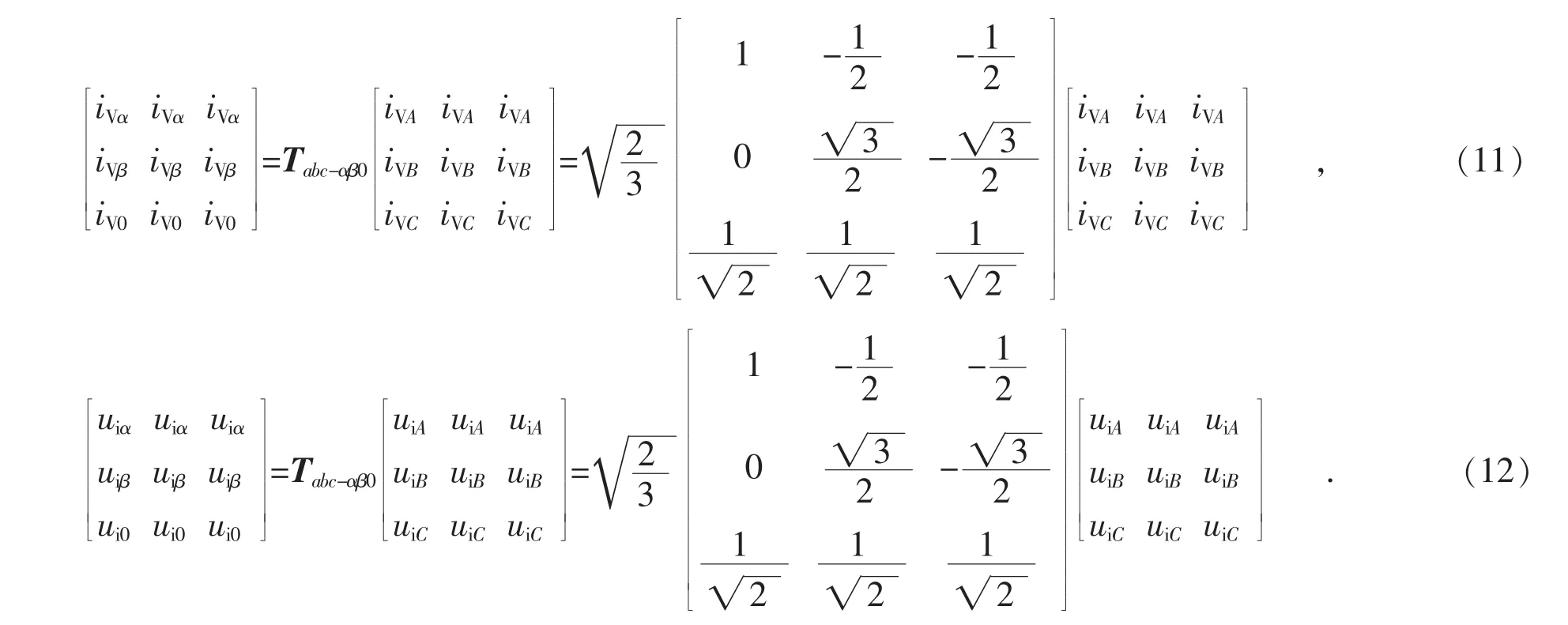
需注意不要将式（10）中u0a，u0b，u0c与图1 中uoa，uob，uoc混淆。

而根据式（3）和式（9）有：

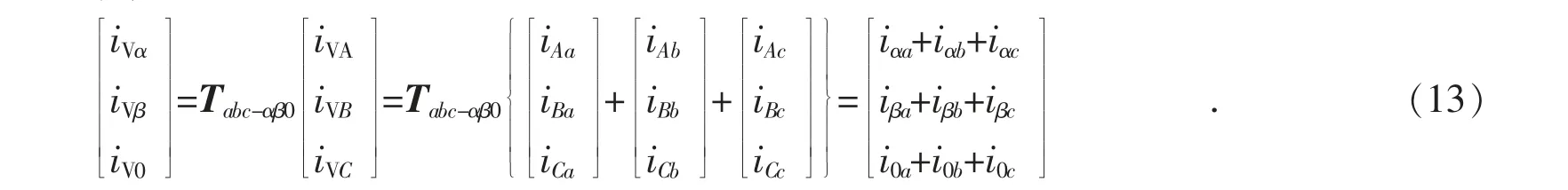
根据式（5）和式（10）有：

另外，对于输出侧abc 坐标系中的各变量，进行abc 坐标系到αβ0 坐标系的变换后，有如下关系式：

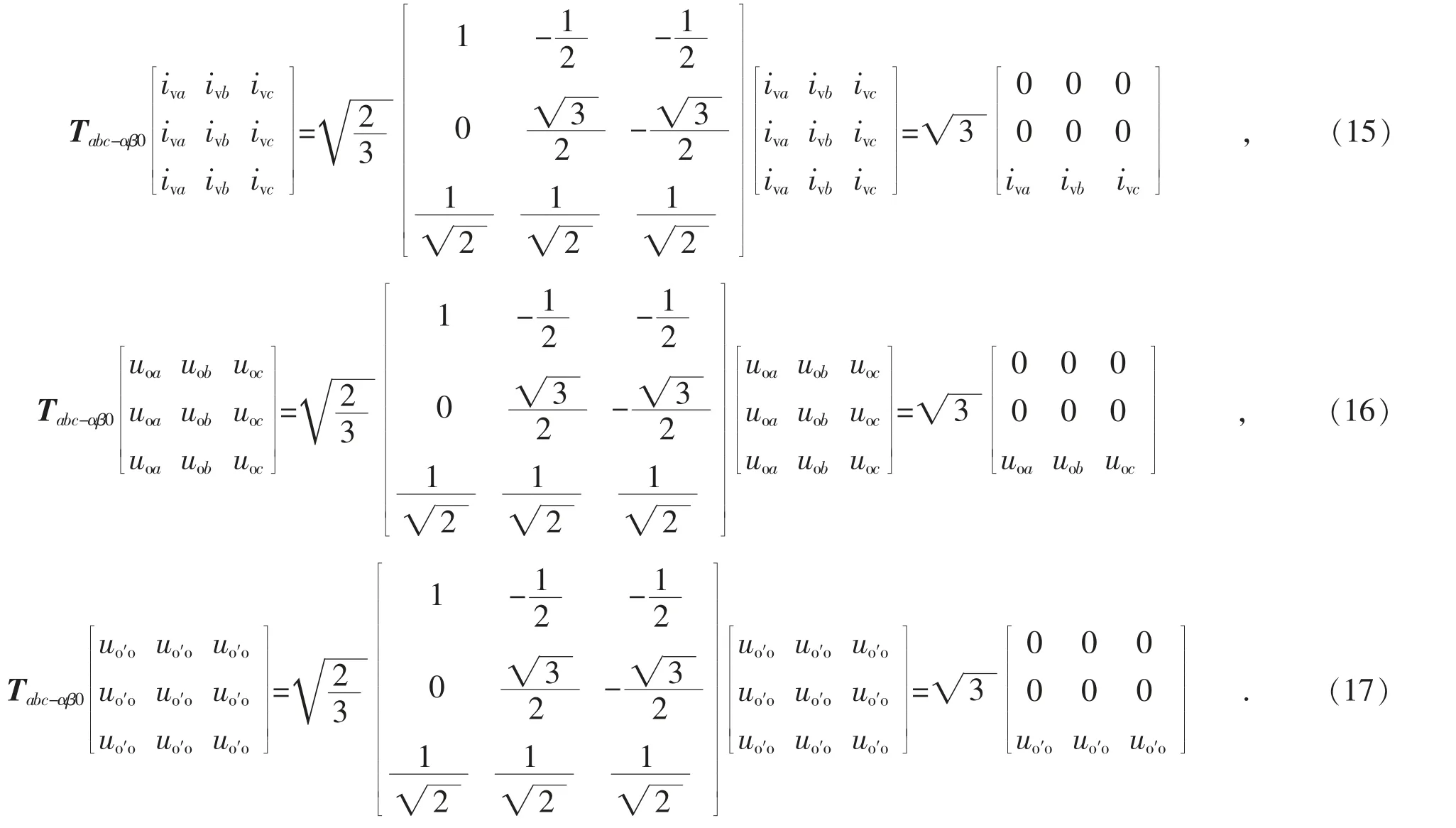
在式（2）两侧左乘Tabc-αβ0可以得到：

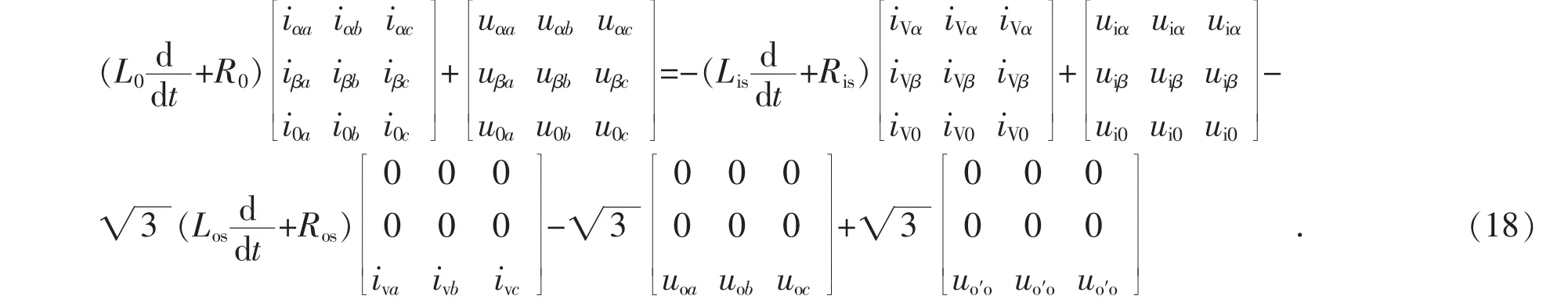
将式（18）拆分成描述输入侧关系和输出侧关系的2 个方程，描述输入侧关系的方程为：

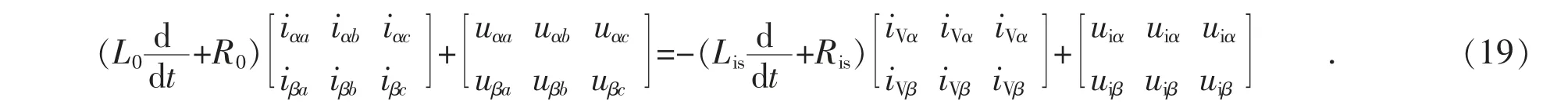
描述输出侧关系的方程为：

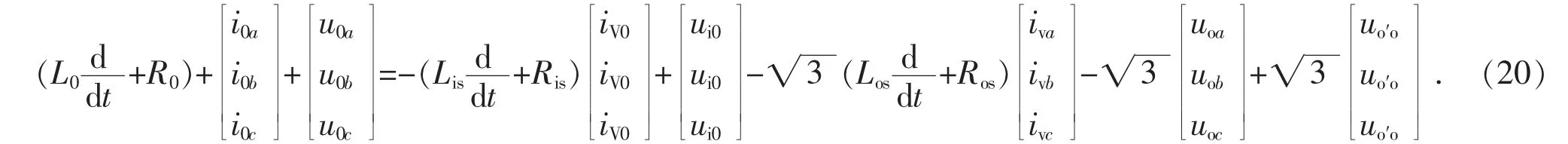
由式（9）知：

由式（10）知：

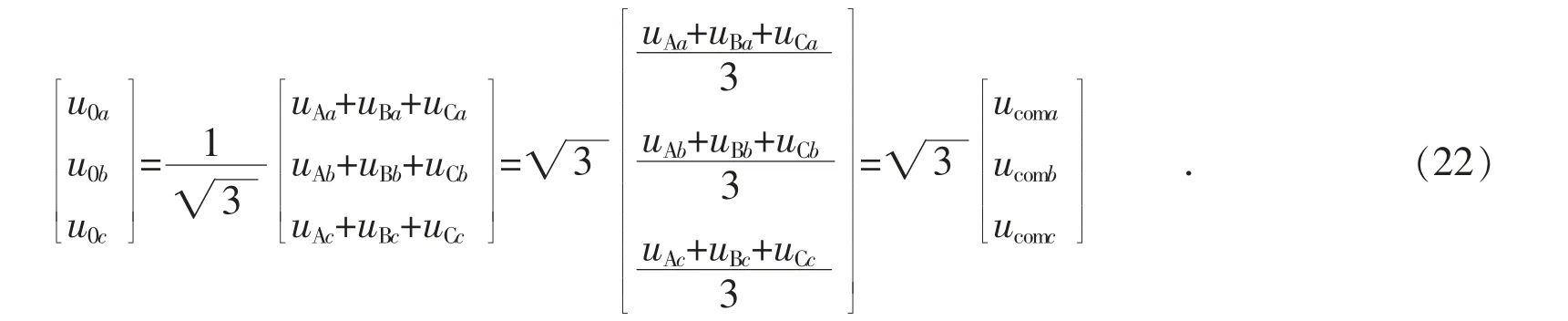
则式（20）可以变为：

整理后有：

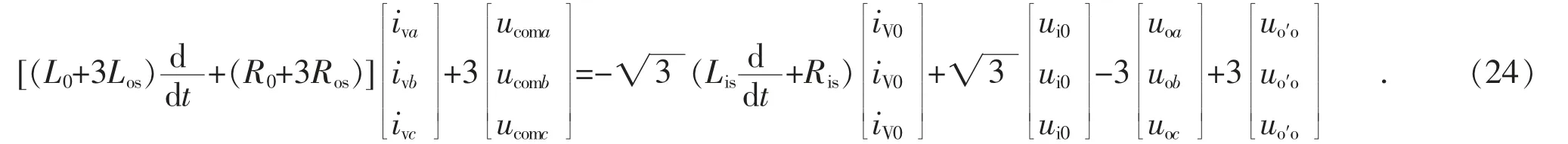
将输出侧abc 坐标系中的各变量变换到αβ0 坐标系，得到：

在式（24）两侧左乘Tabc-αβ0可以得到：

若输入和输出系统三相对称，则有iV0=0，ui0=0，iv0=0，uo0=0，根据式（28）的最后一行有：

此外，根据式（14）和式（26）的最后一行以及式（22）的关系，可以得到usum0=ucom0，从而得到：

去掉式（28）的最后一行后，式（28）可以降阶为：

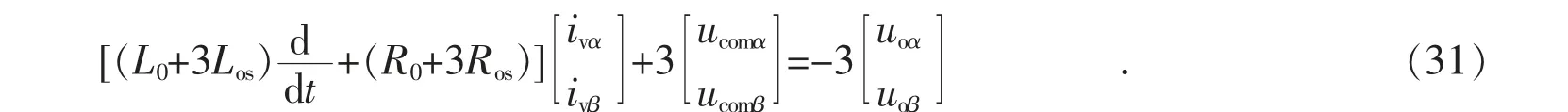
再将式（19）按列拆分成3 个方程：

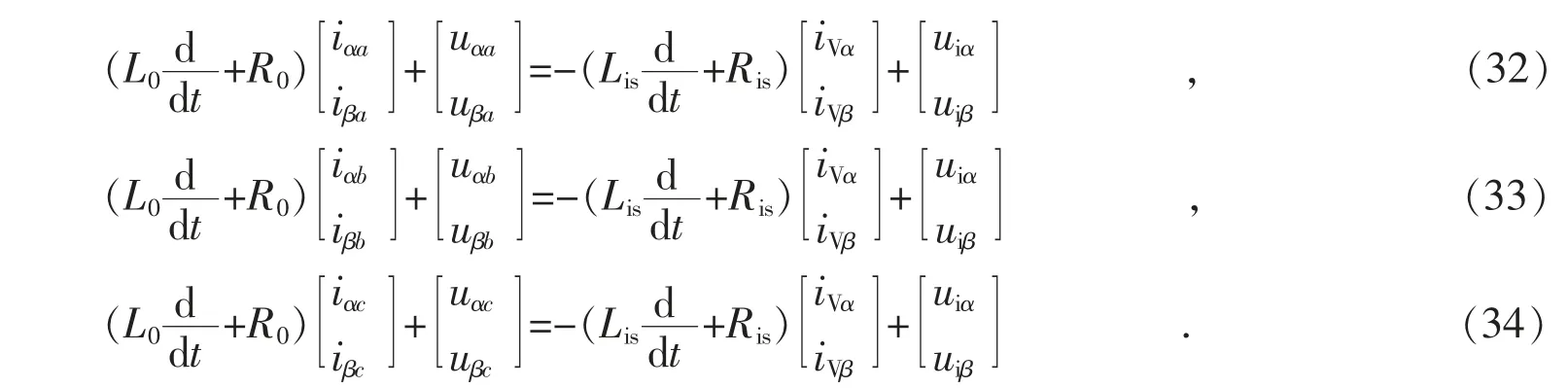
将式（32）、式（33）、式（34）相加有：

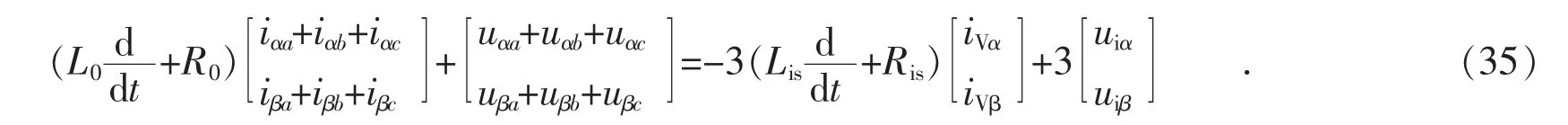
根据式（13）和式（14），式（35）变为：

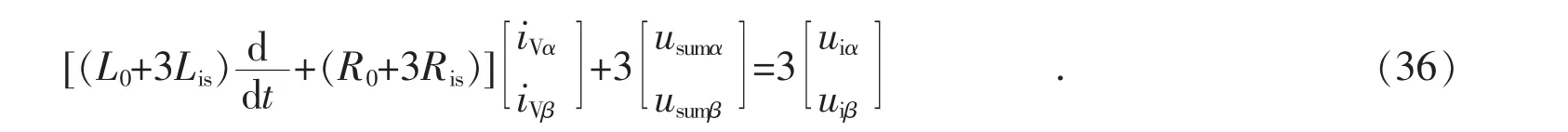
分别将式（33）、式（34）减去式（32），并且定义：

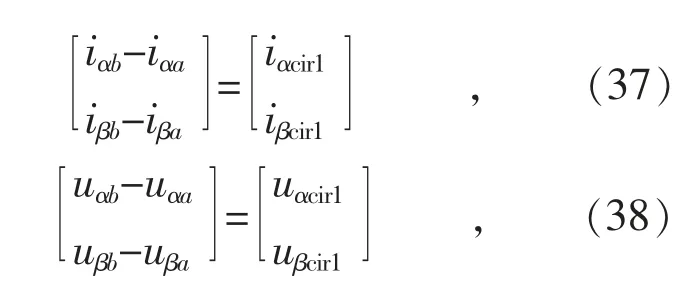
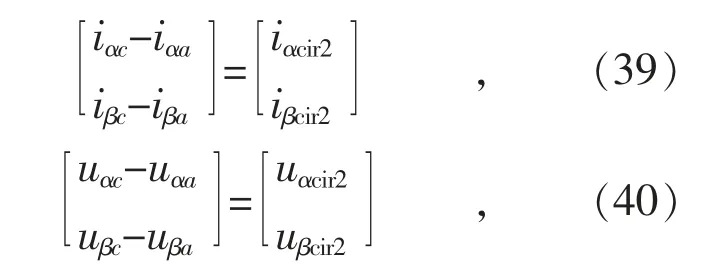
式（37）—（40）中，iαcir1和iβcir1被称为环流1 的αβ分量；iαcir2和iβcir2被称为环 流2 的αβ 分 量；uαcir1和uβcir1被称为环流电压1 的αβ 分量；uαcir2和uβcir2被称为环流电压2 的αβ 分量。

从而可以得到描述环流特性的微分方程为：

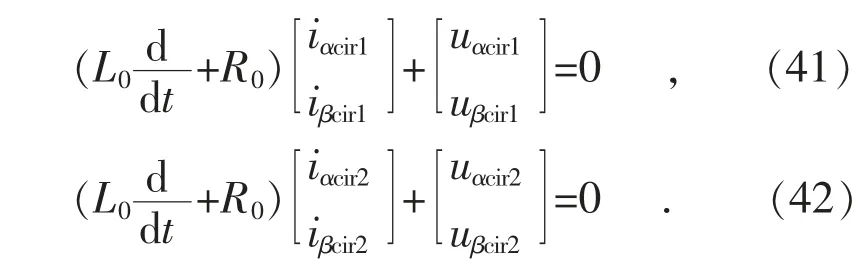
显然，环流特性只由M3C 内部的桥臂电压和桥臂电抗决定，与M3C 的输入侧和输出侧没有直接关系。

式（30）、式（31）、式（36）、式（41）和式（42）构成了对称运行时M3C 在αβ 坐标系中的9 阶数学模型，后面的相关分析和控制器设计将主要基于这个9 阶数学模型进行。

3 M3C 的等效电路推导

根据在αβ 坐标系中描述输入侧和输出侧动态特性的微分方程式（36）和式（31），可以得到：

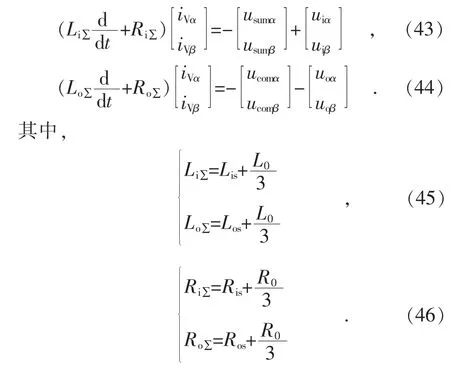
可以得到αβ 坐标系中描述M3C 输入侧和输出侧特性的等效电路如图2 所示。

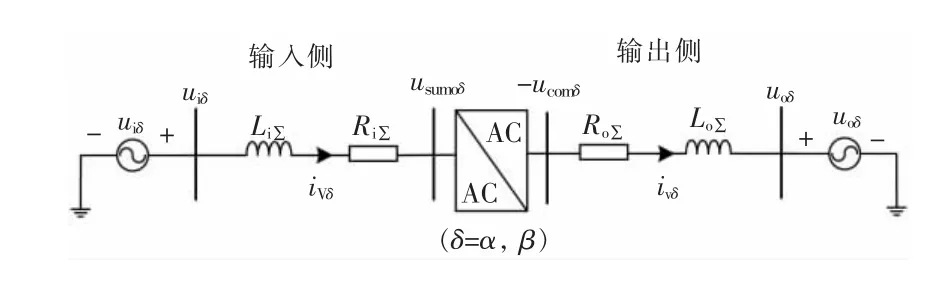
图2 αβ 坐标系中描述M3C 输入侧和输出侧特性的等效电路

同样，根据在αβ 坐标系中描述环流特性的微分方程式（41）和式（42），可以得到αβ 坐标系中描述M3C 环流特性的等效电路如图3 所示。

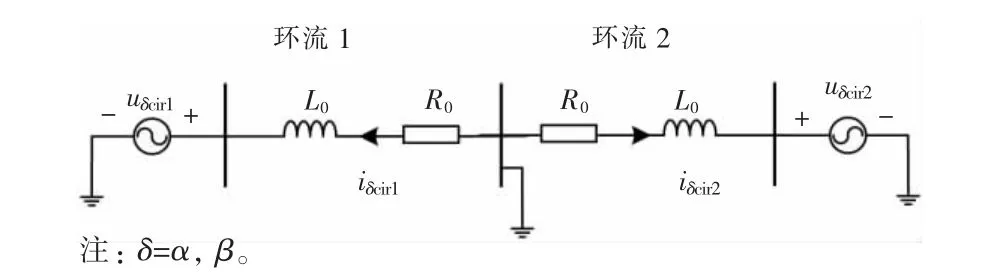
图3 αβ 坐标系中描述M3C 环流特性的等效电路

4 结语

本文针对低频输电中的关键设备M3C，给出了一种方便学习和应用的主回路拓扑结构展示形式和变量命名规则，推导了M3C 的完整数学模型和M3C 在αβ 坐标系中等效电路，可以为后续的M3C 主回路参数设计以及控制器设计奠定基础。