勾股定理中的面积关系
2021-11-18 07:34江苏省太仓市第一中学储怡佳
初中生世界 2021年42期
文/江苏省太仓市第一中学 储怡佳
学习了勾股定理后,大家有没有一个疑问:勾股定理的结论里为什么是2次方,而不是3次方?要明白这个道理,我们可以看图1。在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,分别以a、b、c为边长,向外作正方形,面积分别为S1、S2、S3,我们称这个基本图形为勾股定理的邮票图。由图可知,S1+S2=S3。而正方形面积是边长的平方,因此得出勾股定理的关系式里就是2次方。
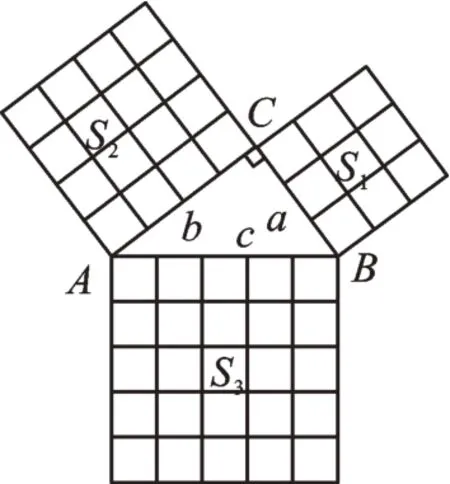
图1
我发现,勾股定理与面积有密不可分的关系。
如果我们把图1中的正方形变成正三角形,此时S1、S2、S3之间是否也有某种关系?如图2,由正三角形的性质和勾股定理,我求出了△ABF的高线长为,同理可得△ACE的高线长为,△BCD的高线长为由此可得S1、S2、S3,并且S1+S2=S3,得到了与图1相同的结果。

图2
如果把图1中的正方形变成半圆,以上的结论还成立吗?如图3,利用圆的面积公式和勾股定理可以求出半圆BC的面积同理可得半圆AC的面积半圆AB的面积,同样得到S1+S2=S3。如果将图3中的半圆AB向上翻折,又能得到什么结论呢?小伙伴们可以动手做一做。

图3
每一个几何定理都是一颗光彩夺目的明珠,值得我们细细品味和欣赏。随着学习的深入,我们一定会发现更有趣的东西。
教师点评
勾股定理是几何学中的明珠,充满了魅力,在数学史上具有独特的贡献和地位,尤其是其中体现出来的“形数统一”的思想方法,更具有科学创新的重大意义。小作者善于开动脑筋,能把课堂内容和课后练习整合起来,思考探究同类问题,并将自己的发现写出来,值得大家学习。
猜你喜欢
小猕猴智力画刊(2021年8期)2021-08-27
孩子(2021年1期)2021-01-27
小学生学习指导(高年级)(2019年10期)2019-11-12
小学生学习指导(高年级)(2018年10期)2018-10-10
中等数学(2018年6期)2018-08-02
福建中学数学(2017年9期)2018-02-05
中学生数理化·七年级数学人教版(2017年2期)2017-03-25
Coco薇(2016年7期)2016-06-28
作文·初中版(2015年10期)2015-10-26
读者·校园版(2014年20期)2014-05-14

