引信-超宽带强电磁脉冲效应阈值试验研究

付胜华，娄文忠，*，苏子龙，郑福泉

(1.北京理工大学 机电学院，北京 100081；2.北京理工大学重庆创新中心，重庆 401120）

引信是利用环境、通过指令信息在预定条件下解除保险，在有利的时机引爆战斗部的控制系统［1］。超宽带强电磁脉冲具有上升前沿陡、峰值功率高和频谱范围宽等特点，可以覆盖多种引信系统的响应频率。引信在超宽带强电磁脉冲环境下极易受到干扰，电磁脉冲会与引信产生效应，并对其造成损伤，使得引信出现早炸、误炸、不炸等多种效应［2-6］。

对引信进行电磁脉冲效应试验，通过测试引信的效应数据，并对效应阈值进行概率拟合，可以有效评估引信在电磁脉冲环境下的易损性［7-8］。经典的数理统计方法是以大样本量为基础，用故障频率代替故障概率，然而在实际的引信效应试验中，试验分析与效应评估如何在小样本条件下对系统的抗电磁脉冲能力做出较为准确评判一直是未解决的难点。

在样本数据处理技术中，贝叶斯分析对效应物在电磁脉冲中的易损性分析中也是一种十分重要的技术手段［7，9-12］。黄忠胜等［13］基于电磁拓扑分析，将分层贝叶斯网络用于电子系统电磁脉冲易损性评估中。孙晓颖等［14］提出了基于贝叶斯网络的系统级电磁易损性评估方法框架，考虑电磁干扰源的各参数对效应物的影响，将事件树分析、EMT等工具有效融入BN评估模型中，为电子系统电磁易损性评估提供了新的分析方法。

本文基于贝叶斯统计理论，针对在超宽带电磁脉冲对引信的效应试验中，面临由于试验费用昂贵，导致试验样本数较少的难题，进行超宽带电磁脉冲对引信效应阈值分析。得到马尔可夫-蒙特卡罗估计的引信在超宽带电磁脉冲环境下，出现的通信故障(不炸）的效应阈值区间。该试验方法为提高引信的抗电磁干扰能力提供了理论基础和试验手段。

1 模型建立

马尔可夫-蒙特卡罗估计在分析参数过程中利用历史数据或专家评估数据的先验分布，进行参数估计得到关于未知参数的后验分布。

设X1，X2，…，Xn为来自总体X的样本，x1，x2，…，xn为其观测值，μ为样本的均值，σ为方差。则二参数正态分布的似然函数为

参数向量(μ，σ2）的后验分布为

通过吉布斯(Gibbs）抽样法进行样本选取［9］，产生马尔可夫链。对于正态分布模型中，当μ给定时，σ2的后验分布为

该马尔可夫链的分布为未知参数的后验分布。基于后验分布如式(6），在平方损失函数下参数向量的蒙特卡罗估计为

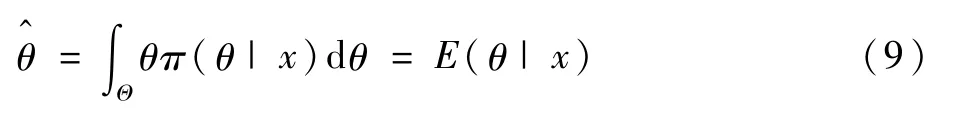
因此，马尔可夫-蒙特卡罗估计主要根据样本均值，依据概率收敛于E(θ｜x）。利用Gibbs抽样法获得π(θ｜x）中的一个非独立样本，形成马尔可夫链，蒙特卡罗进行计算参数向量的估计。

2 引信-电磁脉冲耦合效应试验

引信-电磁脉冲耦合效应试验中采用超宽带电磁脉冲源［8，15］，其脉宽为几纳秒，上升沿小于1 ns(1 ns＝10－9s），频带为10 MHz～2 GHz，该装置可产生垂直极化的辐射场，其结构如图1所示。

图1 超宽带电磁脉冲装置Fig.1 Ultra-wideband strong electromagnetic pulse device

如图2所示，超宽带电磁脉冲源主要由储能电源、Tesla变压器、Blum lien形成线、P-C开关、超宽带天线和控制系统等构成。储能电源充满电后，对Tesla变压器放电，Tesla变压器将电压抬高，电流在Blum lien形成线上形成初级脉冲，初级脉冲经P-C开关后形成强电磁脉冲，由天线辐射至外部空间。

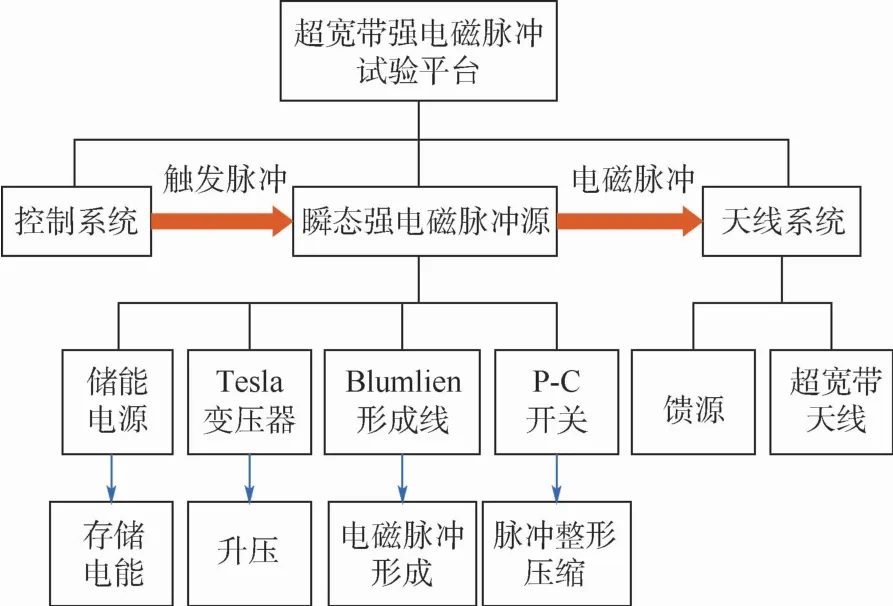
图2 超宽带电磁脉冲装置原理组成Fig.2 Principle of ultra-wideband strong electromagnetic pulse device

引信-电磁脉冲试验根据不同场强、不同重频超宽带强电磁脉冲，对引信辐照下的效应测试。试验采用的引信如图3所示，该引信主要由壳体、通信及控制电路、安保装置及火工品等部分构成。超宽带强电磁脉冲主要对其通信及控制电路起作用，使其通信中断不炸、控制误触发导致早炸或误炸。

图3 测试引信结构原理及样机Fig.3 Test fuze structural principle and prototype

引信-电磁脉冲效应试验系统由强电磁脉冲源、测试引信、电场测试仪、示波器、电磁脉冲控制器、电源等构成。强电磁脉冲源由电磁脉冲控制器发出设定功率与频率的电磁波，电场测试仪与引信放置在一定距离处的电磁场内。示波器A用于监测外部环境中电磁脉冲场；示波器B监测引信中感应电压波形，表征通信是否正常，即判定引信-电磁脉冲阈值。试验原理及现场如图4、图5所示。

图4 试验系统原理Fig.4 Schematic diagram of test system

图5 外场测试Fig.5 Test field diagram

3 试验数据分析

试验中采用1 Hz重复频率，进行引信-超宽带强电磁脉冲的效应试验。设置发送指令周期为10 ms，测试3种状态下引信-强电磁脉冲效应。状态A为电磁波传播方向分别沿引信轴向，状态B为电磁波传播方向分别沿引信径向，状态C为电磁波传播方向分别沿引信轴向与径向构成的平面倾斜45°。设定单次辐照时间为60 s，若引信不受干扰，则认为通过试验。若引信通信中断，且超宽带强电磁脉冲不存在后，引信不能自主恢复工作，导致该引信产生不炸的现象，即为引信-电磁脉冲的效应阈值。试验结果如表1所示。

由表1可知，3种状态的引信在超宽带强电磁脉冲环境下均会受到干扰。引信各个状态的敏感阈值不同。引信在超宽带强电磁脉冲环境下受到干扰，并不是单个脉冲单独作用结果，受干扰过程中有累积效应存在，且引信沿电磁传播垂直方向时，场强全部作用，引信通信中断所需场强值最低，即为明确引信的失效绝对场强阈值，对其引信进行阈值分析。试验数据如表2所示。

表1 重复频率1 Hz引信测试数据Table 1 Fuze test data with 1 H z repetition frequency

表2 引信-电磁脉冲效应阈值Table 2 Fuze-electrom agnetic pu lse effect threshold

根据实测引信的场强阈值，采用马尔可夫-蒙特卡罗估计，用于小样本效应阈值求解后验分布参数。通过数值模拟的方式，根据原始样本数据迭代5 000次得到一条马尔可夫链，使该马尔可夫链的分布为未知参数的后验分布，如图6、图7所示。

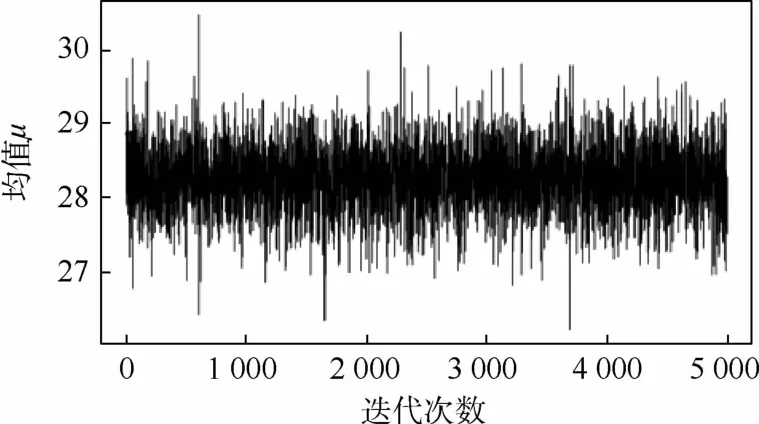
图6 参数μ马尔可夫链Fig.6 Markov chain with para meterμ

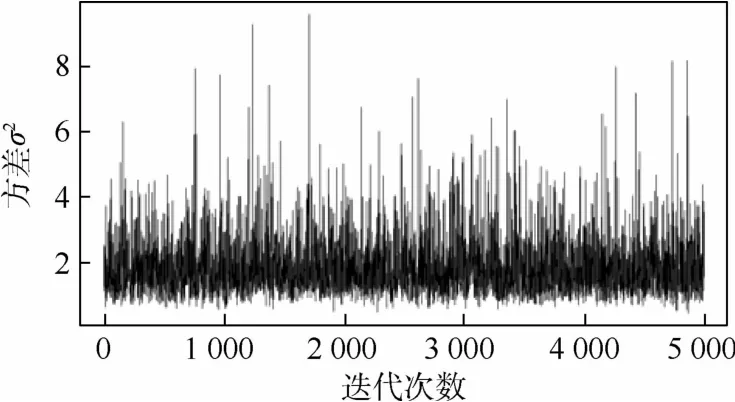
图7 参数σ2马尔可夫链Fig.7 Markov chain with para meterσ2

对生成的马尔可夫链数据样本进行蒙特卡罗估计。如图8、图9所示，得到引信-强电磁脉冲效应的阈值的均值后验期望估计为28.262 kV／m，均值的95%可信区间为(27.390，29.129）kV／m；阈值的方差后验期望估计为1.867 kV／m，方差的95%可信区间为(0.834，4.182）kV／m。即在此电磁场强分布下，引信出现引信通信中断的不炸失效阈值区间。

图8 效应阈值概率密度函数Fig.8 Effect threshold probability density function

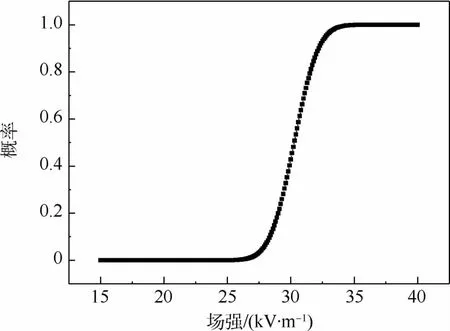
图9 效应阈值概率分布Fig.9 Effect threshold probability distribution

4 结论

1）依据超宽带强电磁脉冲模拟器，进行引信-强电磁脉冲的效应试验，得到在超宽带强电磁脉冲环境下，引信会出现通信中断(不炸）、正常等数值。

2）引信-电磁脉冲效应阈值处在一定范围内，其通讯中断不炸的效应阈值均值为28.262 kV／m，均值的95%可信区间为(27.390，29.129）kV／m。阈值方差的后验期望估计为1.867 kV／m，方差的95%可信区间为(0.834，4.182）kV／m。

本文模型提供了一种在强电磁干扰下的引信通信中断失效阈值的估计方法，为引信抗电磁干扰分析，避免早炸、误炸、不炸等可靠性涉及提供了试验方法和数据支撑。