含间隙非线性机翼跨声速颤振时滞反馈控制

聂雪媛，郑冠男，杨国伟

(中国科学院力学研究所 流固耦合系统力学重点实验室，北京 100190）

气动力与柔性结构相互作用会产生气动弹性，颤振是气动弹性领域中最危险的一类动不稳定现象，极易引发灾难性事故。颤振主动控制技术是目前研究最多的颤振抑制方法，一般是通过在机翼上布置多个控制面，控制其偏转改变作用在机翼上的气动力，以达到抑制颤振的目的。

主动控制气动弹性系统包含作动器、传感器、控制器和数字滤波器等元器件，其动态特性会导致最终作用于结构的控制力产生时滞［1-2］。时滞会破坏控制器的控制性能，甚至导致被控系统失稳。在气动弹性领域，已有学者对此现象展开了研究。国内，Zhao［3］对不可压流场反馈通道存在延时的翼型气弹稳定性进行了研究，指出在飞行器气动伺服弹性设计时，不可忽略时滞影响。Huang等［4］分析了输入延时对不可压流场的飞行器稳定性的影响，并提出了一种最优控制方法抑制颤振。Cai等［5-6］针对前向通道存在时延，采用控制和滑模变结构控制方法对二元翼型颤振进行控制，指出不考虑时滞所设计的控制器无法有效抑制延时系统的颤振。Xu等［7］研究了超声速下时滞对气动弹性系统颤振边界稳定性的影响。国外，Ramesh和Narayanan［8］对超声速下反馈通道存在时滞的翼型，设计了状态反馈控制方法。Marzocca等［9］研究了考虑时滞存在时，对线性和非线性控制器作用下的二维翼型气动弹性系统稳定性的影响。Araujo和Santos［10］采用Smith预估方法研究了对控制通道存在不同时滞的颤振抑制效果。

就目前已有文献来看，针对考虑时滞的颤振主动控制研究几乎都集中在亚、超声速域，气动力计算基于线化气动力模型，结构视为线性结构。然而，现代民用／军用飞机大都以跨声速巡航，激波位置对结构响应影响敏感，较为精确的模拟气动力非线性的方法是计算流体力学(CFD），但该方法计算量太大，且难以用于控制器设计。此外，机翼控制面的铰链处普遍具有间隙，会引起刚度非线性现象［2］，间隙非线性对气动弹性有显著影响，在分析带控制面的机翼颤振问题时，必须加以考虑。

针对以上问题，本文基于气动力降阶模型(Reduced Order Model，ROM）技术，以含间隙非线性的二维翼型为对象，对输入信号存在延时的控制系统展开了跨声速机翼颤振时滞反馈主动控制方法的研究。通过状态变换，将时滞被控系统转换为不显含时滞的状态方程，进行最优时滞反馈控制。在数值仿真中，采用自适应时间步长以准确捕捉结构间隙切换点。

1 基于CFD／ROM 的气动弹性模型

在跨声速域，CFD方法能提供精确的非定常气动力。本文通过CFD／CSD耦合方法，以白噪声信号作为结构位移输入，通过系统辨识技术建立非定常气动力的自回归滑动平均(Auto Regressive Moving Average，ARMA）降阶模型。

1.1 控制方程

气动力计算采用基于RANS的三维Navier-Stokes控制方程，守恒型的流动方程可表示为

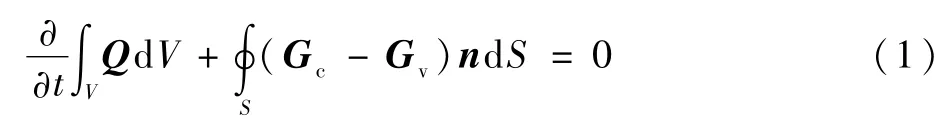
式中：Q为守恒向量；Gc和Gv分别为对流通量和黏性通量；S为控制体V的边界面积；n为面的法向量；t为物理时间。

方程(1）对无黏项离散采用Roe格式，黏性项离散采用二阶中心差分格式，时间推进采用双时间步。

1.2 结构运动方程

本文以含间隙非线性的带控制面二维翼型(见图1）作为研究对象，俯仰方向结构刚度含有间隙非线性，非线性广义“位移-力”关系如图2所示。

图1 带控制面的二元翼型Fig.1 Two-dimensional airfoil with control surface

图2 间隙非线性Fig.2 Free-play nonlinearity

式中：M代表回复力矩，¯M(α）为分段线性函数，α为俯仰角；kα为俯仰方向的刚度系数；δ为间隙角阈值。

二元翼型的非线性控制方程可写为

式中：h为沉浮位移；b为机翼半弦长；kh为沉浮方向刚度系数；m为机翼质量；Iα为机翼惯性矩；xα为弹性轴到机翼重心的无量纲距离；L和M 分别为气动力和力矩。

其中：μ＝m／(ρπb2）；Ma∞＝U∞／a∞；Cl和Cm分别为升力和俯仰力矩系数；ρ为来流密度。

定义xs＝［ξ α］T，则式(4）可转换为状态空间形式：

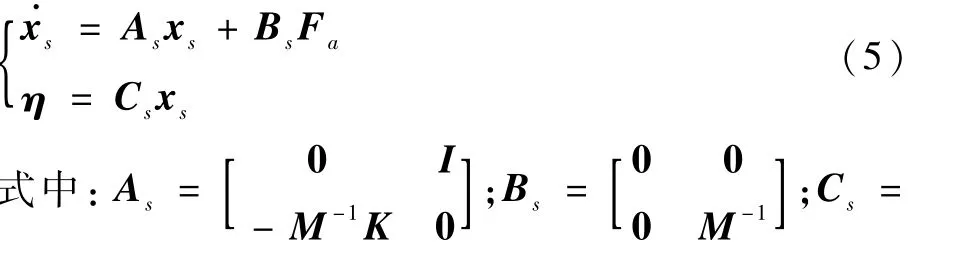
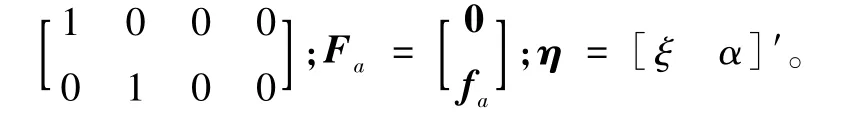
1.3 基于ARM A的开环气动弹性模型

对于模型辨识而言，最重要的是激励信号的选取。一般来说，要求激励信号能够激起被辨识系统所关心的所有频段的信号。本文选取随机信号作为结构位移，与CFD耦合，计算得到在该激励下的气动力输出。对输入白噪声，输出非定常气动力的信号采用系统辨识方法，选用ARMA差分模型对气动力建模。该模型具有时间域离散形式，如下：

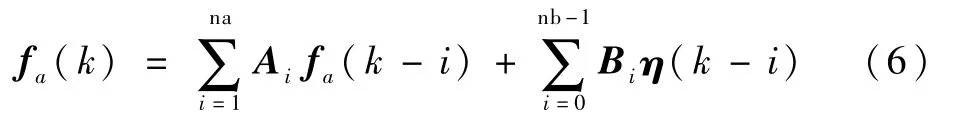
式中：fa代表气动力向量；η为结构位移输入向量；A、B为要辨识的系统模型参数；na和nb分别为输出和输入的延迟阶数。

方程(6）通过变量代换，可以化为状态方程离散形式(见(7）），具体推导过程可详见文献［11］。

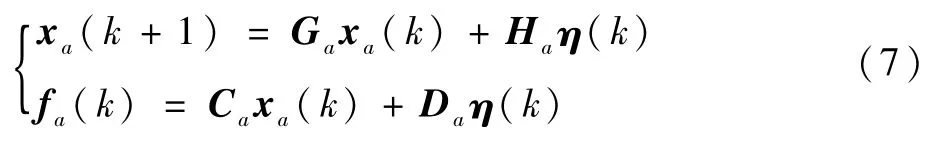
由于结构方程为连续系统，需要对气动力离散结构转换为连续系统，通过双边变换，可得气动力的连续系统状态空间为

将方程(5）与方程(8）耦合，可得开环气动弹性模型为

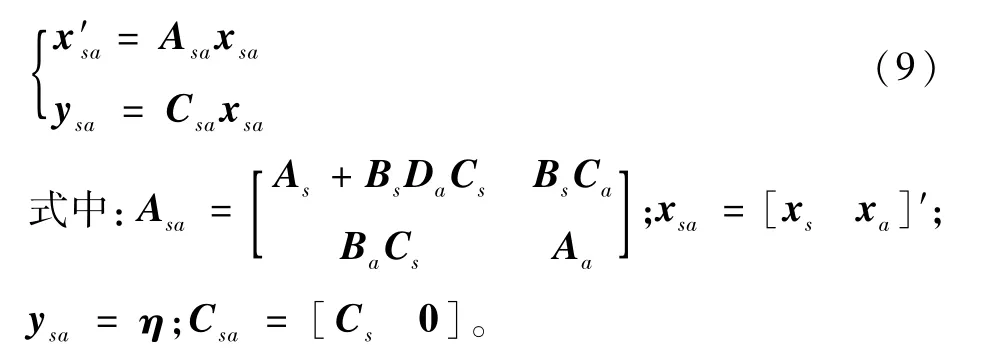
值得注意的是，从式(9）可以看出，该方程中系数矩阵Asa包含分段线性函数(α），因此该方程为非线性方程。由于间隙非线性属于不光滑非线性，本文所研究的结构具有2个切换点±δ(见图2），若采用时间步长固定的龙格库塔方法求解，将无法准确捕捉到间隙非线性切换点的变化。为此，本文采用二分法［12］搜索切换点确定自适应时间步长的龙格库塔法对式(9）进行求解。

2 时滞反馈主动控制设计

2.1 时滞控制系统

对式(9）所描述的气动弹性模型，可通过控制面偏转，其目的是引入附加气动力来抑制颤振。引入控制作用后的闭环气动弹性结构框图如图3所示(开关拨到1点，不考虑控制信号的延时）。

图3 气动弹性系统闭环控制框图Fig.3 Block diagram of closed-loop control of aeroelastic system

图3中：β为控制面偏转角，代表控制器输出量，fca为控制面偏转角偏转引起的气动力。λ为时滞。该气动力模型采用1.3节方法建立了控制面偏转气动力降阶模型：

式中：xc为控制面偏转状态变量；Aca、Bca、Cca、Dca为该模型的系数矩阵。

将式(9）和式(10）合并，即可得广义被控对象模型为

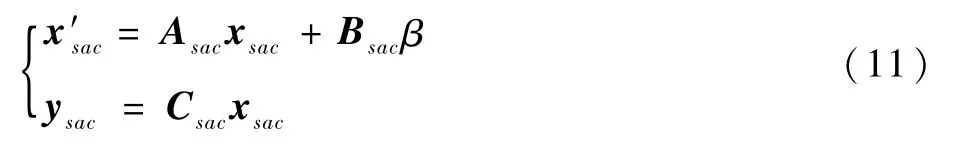
当控制器存在时滞λ时(即在如图3所示的控制系统中开关拨到点2），广义被控对象模型可描述为

2.2 考虑时滞的控制方法设计

定义变量z(t）如下：

将该变量代入式(12a），由文献［13］可知，式(12a）可变为不显含时滞的系统：

可以证明，只要系统(12a）是完全可控的，则系统(14）也是完全可控的。

当时滞λ已知时，式(14）所描述的系统为分段线性系统(考虑结构间隙非线性，系数Asac为分段线性矩阵），本文对分段子系统采用最优反馈控制，通过极小化式(15）所示的目标函数，获得控制器最优控制量β。

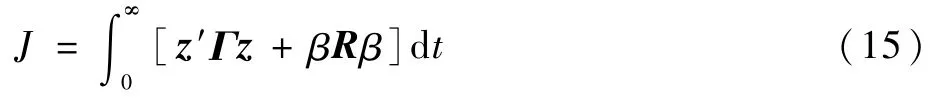
式中：Γ和R分别为状态变量和控制变量的加权矩阵。

控制器的输出最优控制量为

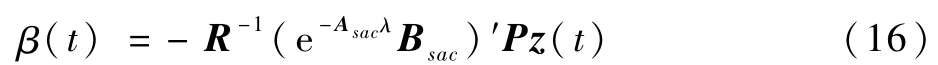
式中：P为Ricatti方程的解。

对式(14）所示的分段线性系统采用式(16）所示的最优控制，即可实现颤振主动控制。

由式(13）可知，实际系统状态变量xsac的求解中包含了积分项s，对于任意时滞λ，总可以写成λ＝lT－n，T为连续系统采样周期，l为大于0的整数，0≤n＜T。在实际控制中，控制器输出的控制量通过保持器将数字电路中的离散信号转换为连续信号，以零阶保持器为例：

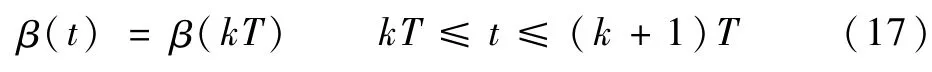
基于上述思路，通过积分变量替换，式(13）中的积分项可以用不同历史采样时刻的控制量来表示［14］。

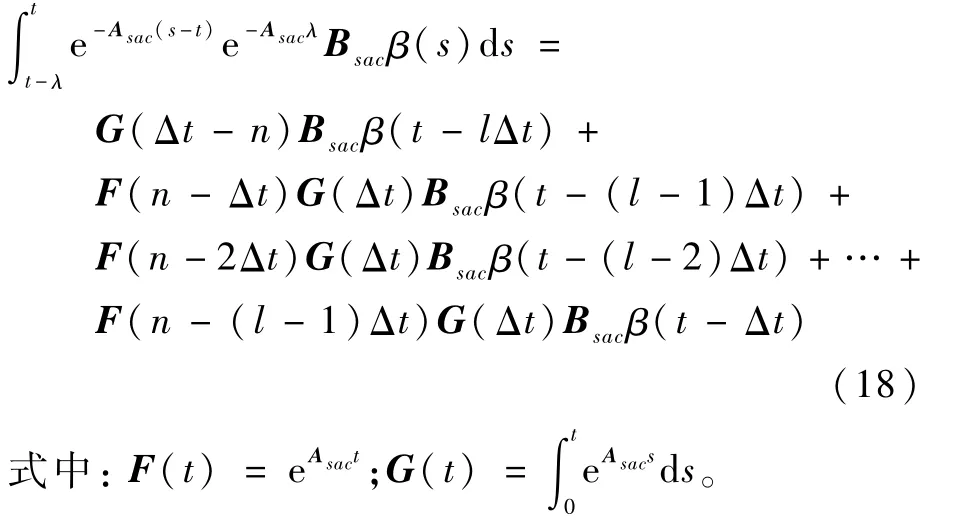
由式(18）可以看出，系统当前时刻的状态与控制量的历史数据相关，而历史数据的长度则取决于时滞λ的大小。

3 算例与分析

以图1所示的含间隙非线性二元机翼为例［15-16］，考虑控制信号存在时滞，对跨声速机翼颤振进行主动控制。该模型无量纲参数设置选自文献［15］，如表1所示。计算工况为马赫数Ma∞＝0.8，迎角为0°。

表1 模型无量纲参数Table 1 Non-dimensional parameters of model

以滤波白噪声作为结构位移，辨识得到非定常气动力离散模型(7），通过双边变换，最终得到连续状态方程(8）。

为验证辨识模型的准确性，先以常用的3211信号作为位移η的给定输入，进行CFD非定常气动力计算，并与模型(8）的计算输出结果进行比较，如图4所示。

图4 3211信号激励下ROM和CFD计算的气动力结果比较Fig.4 Comparison of aerodynamic forces with ROM and CFD excited by 3211 signals

进一步，按照文献［15］设置初始扰动，即选取结构位移初值xs0＝［0 0.002 8 0 0.001］T，在Ma∞＝0.8U*＝1.48工况下，计算气动力降阶模型与结构耦合的开环气弹模型(9）的响应，并与CFD／CSD直接耦合得到的结果进行比较，如图5所示。可以看出，基于气动力降阶模型得到的开环模型(9）具有较高计算精度，能够替代CFD／CSD的直接耦合计算。

图5 ROM和CFD结算结构响应结果比较(Ma∞＝0.8U* ＝1.48）Fig.5 Comparison of structure response resultwith ROM and CFD(Ma∞＝0.8U* ＝1.48）

图6给出了该工况下俯仰角的相轨迹。可以看出，俯仰角从初始位置(0.002 8，0.01）出发，在气动力的作用下逐渐向原点位置收敛，结构是稳定的。继续增大U*，当U*＝1.72时(文献［15］在该工况初始条件下U*＝1.7），系统出现极限环振荡，如图7所示。

图6 俯仰角相轨迹(Ma∞＝0.8U* ＝1.48）Fig.6 Phrase portrait of pitch angle at Ma∞＝0.8U* ＝1.48

针对图7所发生的极限环振动，采用控制面偏转的方式加以控制。图8为给定控制面板偏转3211信号、CFD计算结果与白噪声信号辨识得到的气动力模型(10）的结果比较。

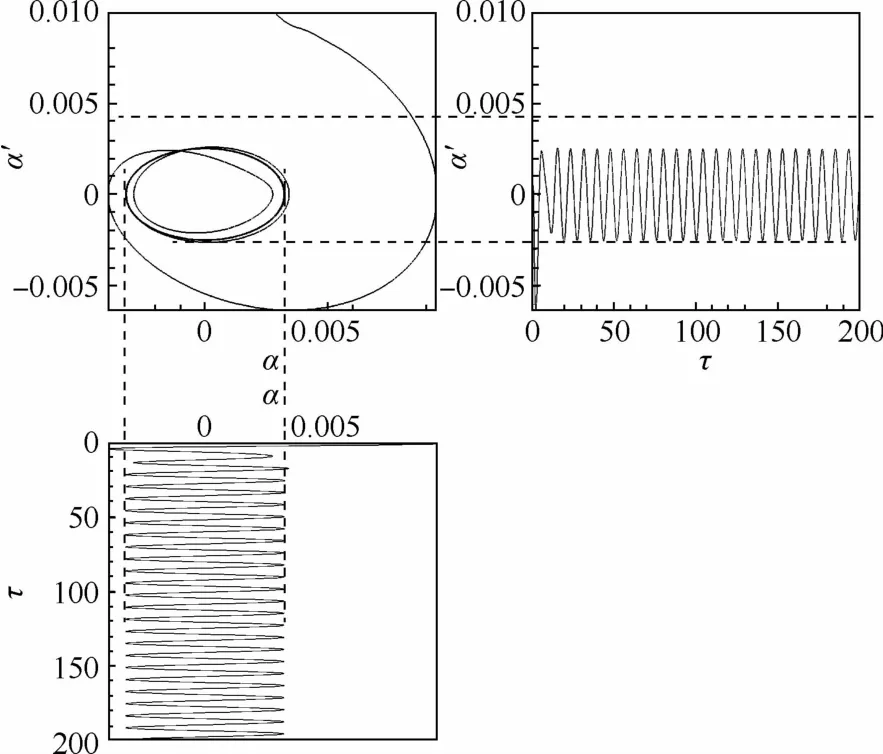
图7 俯仰方向极限环振荡(Ma∞＝0.8U* ＝1.48）Fig.7 Limit-cycle oscillation of pitch at Ma∞＝0.8U* ＝1.48

图8 3211信号控制面偏转输入控制面ROM和CFD计算的气动力结果比较Fig.8 Comparison of control surface aerodynamic forces with ROM and CFD excited by 3211 deflection input signals

若控制通道不存在时滞，即图3所示开关接通触点1，此时采用常规的最优控制方法即可控制住颤振，如图9所示。控制器输出控制量的变化如图10所示。考虑到系统(11）状态的可观测性，本算例对式(15）中的状态加权矩阵Q选为对角阵，对角线元素为100，控制加权矩阵R设为50。

图9 无时滞系统颤振控制效果Fig.9 Flutter control result for system without delay

图10 闭环控制系统控制面偏转角Fig.10 Control surface deflection of closed-loop control system

若图3所示系统控制信号存在时滞，即开关接通触点2，继续采用不考虑时滞的控制方法，在时滞λ较小时，控制方法是有效的。但当增大到一定值时(本算例中为无量纲时间0.37，T＝0.05），其控制后的系统响应相轨迹如图11所示。可以看出，即使控制面偏转到最大可允许偏转角，但结构响应的相轨迹在整个相平面发散，系统出现失稳，控制方法失效。

图11 时滞系统的无时滞控制相平面图及控制面偏转角Fig.11 Phase portrait of no delay control for system with time delay and corresponding control surface deflection

在这种情况下，采用本文提出的考虑延时设计的控制方法(16），对该系统进行颤振控制，此时l＝8，m ＝0.03，控制后的结构位移相轨迹如图12所示。

从图12可以看出，在控制作用下，翼型位移从初始状态，出发，在相平面内其运动轨迹形成一条封闭曲线，收敛于各自的平衡态(0，0）。

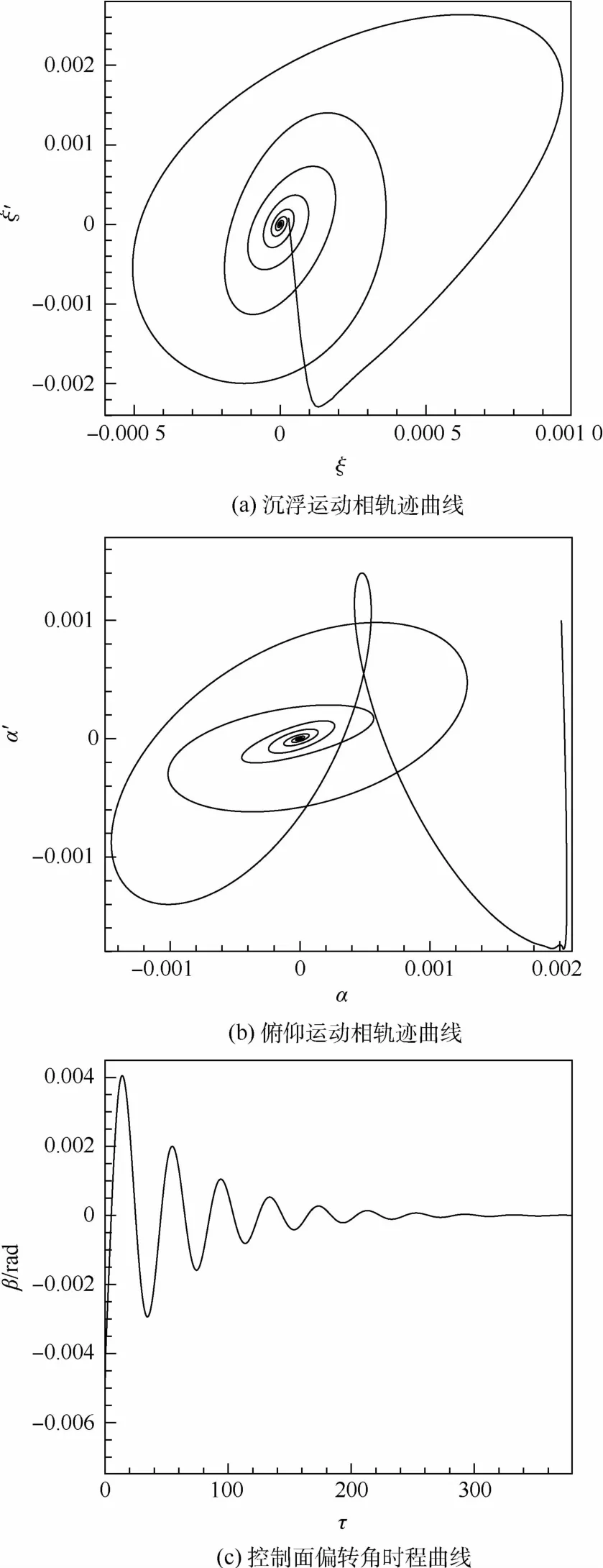
图12 考虑时滞的控制器对时滞系统颤振控制的相平面图及控制面偏转角(λ＝0.37）Fig.12 Phase portrait of flutter control for system with time delay exerted by controller designed with time delay and corresponding control surface deflection atλ＝0.37

继续增大时滞，图13为无量纲时滞λ＝1.6时，颤振控制的翼型位移相轨迹及控制面偏转角。可以看出，考虑时滞设计的控制方法在大时滞下仍然有效。

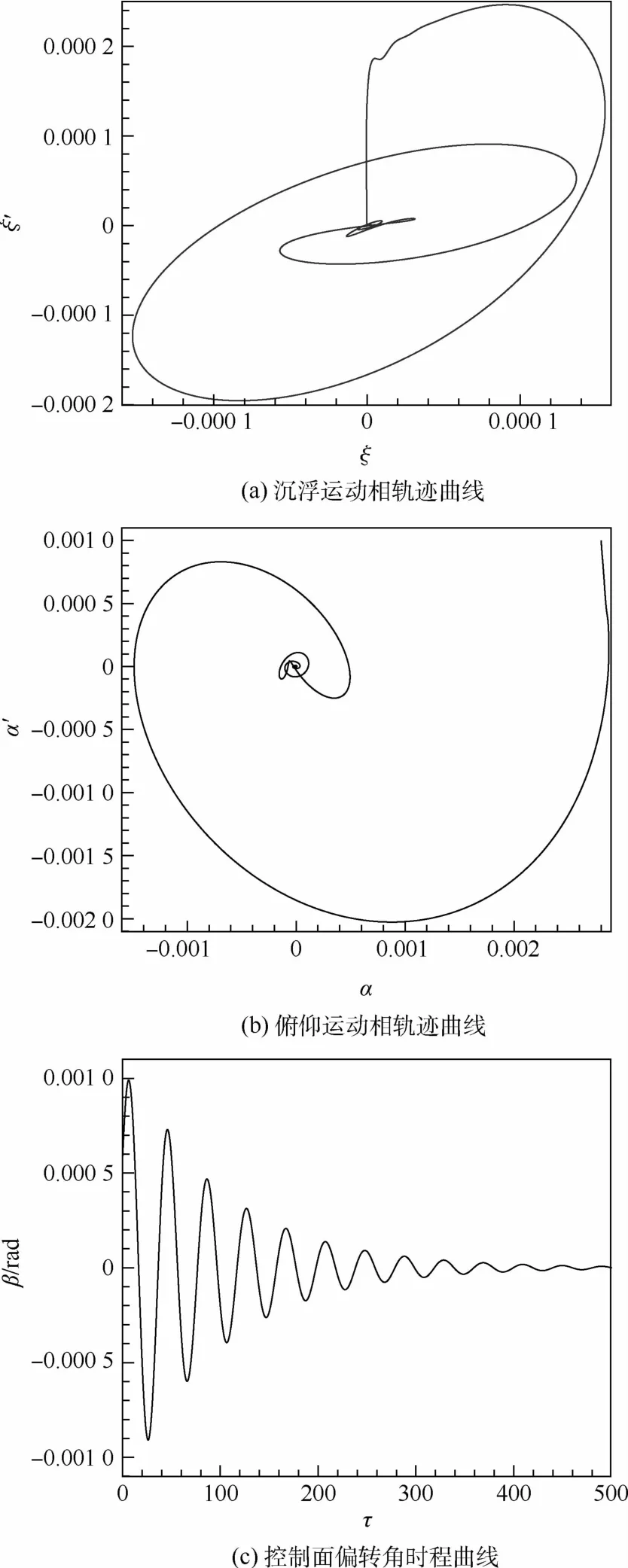
图13 考虑时滞的控制器对时滞系统颤振控制的相平面图及控制面偏转角(λ＝1.6）Fig.13 Phase portrait of flutter control for system with time delay exerted by controller designed with time delay and corresponding control surface deflection atλ＝1.6

4 结论

1）跨声速下，以含间隙非线性的翼型为研究对象，对输入信号存在时滞的闭环气动弹性系统颤振主动控制方法进行了研究。基于非定常气动力降阶模型结合间隙非线性具有分段线性的特点，建立了非线性被控气动弹性模型，通过引入含积分项的状态变换，将时滞被控系统转换为无时滞系统，并在此基础上进行最优反馈控制设计，所设计的控制量考虑了时滞的影响。

2）使用针对无时滞系统所设计的控制方法，对存在时滞的系统进行颤振主动控制，其控制效果随时滞增大而减弱，直到增大到某一临界值(本算例为无量纲时间0.37）时，控制方法失效；本文提出的时滞反馈控制方法能有效地处理控制通道的时滞，实现颤振主动抑制，可行性不受时滞大小的影响。

下一步工作将在此基础上，考虑不确定时滞对气动弹性系统稳定性的影响，时滞不再是事先确定的常数，应研究如何设计控制方法提高系统的稳定性。