多曝光星敏感器的全运动参数建模及优化设计

于文波，武佩，宣传忠，张春慧，江洁

(1.内蒙古农业大学 机电工程学院，呼和浩特 010018；2.北京航空航天大学 仪器科学与光电工程学院，北京 100083）

星敏感器是目前已知的最高精度姿态测量仪器，其以高精度、自主性和无漂移等优点，在航天、航空、航海等各类导航任务中均获得了广泛应用［1-3］，举世瞩目的北斗导航卫星即采用星敏感器作为自身核心导航部件［4］。传统星敏感器主要工作于静态或低速运动场合，且姿态更新率较低；但是，随着航空航天技术的不断发展，某些快速机动导航任务，如敏捷卫星、空间武器或弹道导弹等，不仅要求星敏感器具有高动态性能［5-7］，还要求其必须具有高姿态更新率特性［8］。这是因为随着载体机动性提高，其姿态变化率增大，星敏感器的姿态更新率必须同步提高，才能实现从离散测量数据到载体连续变化姿态数据的精准刻画与有效恢复。

为了提升星敏感器的姿态更新率，钟红军［9］与毛晓楠［10］等将星敏感器工作过程大体分为星图曝光成像、星图像素数据传输与处理、星跟踪与姿态解算3个阶段，并提出一种并行流水线处理方法，使得更新率大小由上述三者中耗时最长的阶段决定，从而提高星敏感器的姿态更新率。对于传统星敏感器，由于所用图像探测器的恒星探测灵敏度较低，必须以长曝光时间获得足够灵敏度，曝光时间是其姿态更新率的主要瓶颈；为了减小曝光时间，有学者将高灵敏度图像探测器(如电子倍增电荷耦合器、像增强型图像探测器等）引入星敏感器领域，曝光时间的缩短在一定程度上提高了星敏感器的姿态更新率［11-12］，此时，星图像素数据传输与处理时间成为姿态更新率的新瓶颈。为了减小星图像素数据处理时间，笔者提出了一种多路星点质心提取方法［13］，利用并行处理思想对星图像素数据进行处理、提取星点质心结果，有效减小了像素数据处理时间，进而提高姿态更新率，但像素数据传输时间受到图像探测器本身输出能力的制约，无法显著减小。

为了全面提升姿态更新率，笔者在前期研究中，提出了一种基于像增强型图像探测器的多曝光成像方法［14］。该方法能够根据载体机动角速度大小自适应插入N次短时间曝光，从而实现在单帧星图中记录N个时刻的星点位置信息，当分别按照N个成像时刻进行星跟踪与姿态解算时，可以得到N个时刻对应的姿态信息，从而等效为将姿态更新率提高N倍。尽管上述方法的应用前景较为可观，但其在实际应用中存在如下问题：随着星敏感器的运动角速度及角加速度增大，多曝光成像的星点轨迹长度增加，若星敏感器的极限敏感星等、视场大小等光学参数与角速度及角加速度等运动参数不匹配，则相邻轨迹出现相互交叉问题的概率显著增大，这将严重影响后续的星点质心提取及姿态跟踪解算，从而影响多曝光成像方法的性能。

为此，本文进一步对多曝光成像方法进行深入研究。首先，建立了复杂运动条件下全像面星点成像位置模型；然后，据此对星敏感器的极限敏感星等、视场大小等光学参数与角速度及角加速度等运动参数进行最优化匹配设计与仿真分析；最后，基于上述优化参数设计星敏感器，进行外场观星实验，实验结果验证了所提方法的有效性。

1 多曝光星敏感器的基本工作原理

多曝光星敏感器的基本工作原理如图1(c）所示，为了对照说明，图1(a）、(b）分别给出了传统星敏感器与现有像增强型星敏感器的基本工作原理［14］。图1中，阶段1、阶段2、阶段3分别对应星敏感器的3个流水线工作阶段，即星图曝光成像、星图像素数据传输与处理、星跟踪与姿态解算，Te、Tp和Tq分别为上述3个阶段所需的处理时间，T为星敏感器的工作周期，F为星敏感器的姿态更新率。

对于传统星敏感器，如图1(a）所示，由于图像探测器灵敏度较低，必须以长曝光时间获得足够的灵敏度。因此，长曝光时间Te是传统星敏感器姿态更新率F的主要瓶颈。对于现有像增强型星敏感器，像增强器的引入，能够对微弱的星光信号进行显著放大，从而极大缩短了星敏感器的曝光时间Te，在一定程度上提高了姿态更新率F。然而，如图1(b）所示，曝光时间缩短后，星图像素数据传输与处理成为流水线中耗时最长的阶段。特别的，当大面阵图像探测器应用于星敏感器领域时，这一阶段的耗时Tp更长，极大限制了姿态更新率F的进一步提高。

图1 不同曝光工作模式下的星敏感器流水线示意图Fig.1 Schematic diagram of workflow of star trackers in different exposure modes

为了突破星图像素数据传输与处理时间Tp对姿态更新率F的制约，笔者提出了一种像增强型星敏感器的多曝光成像方法［14］，其流水线工作原理如图1(c）所示。由于像增强型星敏感器的曝光时间Te远小于处理时间Tp，在较长的时间Tp内不只可以进行一次短时曝光，而是可以插入N个短时间采样曝光Te，N为多曝光成像次数。此时，单帧星图实际上记录了星点在N个时刻的成像信息，当分别按照成像时刻对其进行星跟踪与姿态解算时，可以得到N个时刻对应的姿态信息，从而等效为将星敏感器的姿态更新率F提高N倍。

需要注意的是，多曝光成像方法主要适用于动态场合，当星敏感器处于静态时，将导致多曝光成像星点混叠，从而无法利用混叠星点信息解算出星敏感器对应时刻的姿态。仿真实验表明［14］，随着星敏感器运动角速度逐渐增大至20(°）／s，相应的姿态更新率F最高可达210 Hz，远高于现有更新率技术的10 Hz水平。

然而，上述方法在实际应用中存在如下问题：随着星敏感器的全运动参数(包括运动角速度及角加速度）逐渐增大，多曝光成像星点的运动位移增加，若全运动参数与星敏感器的极限敏感星等、视场大小等参数不匹配，则相邻星点轨迹相互交叉情况的发生概率显著增大，这将严重影响后续的星点质心提取及姿态跟踪解算，从而影响多曝光成像方法的性能。为此，下面对多曝光星敏感器的全运动参数进行定量建模分析。

2 全运动参数建模分析

图2为单颗导航星的多曝光成像示意图。若A(t）表示t时刻星敏感器的姿态矩阵，vi(t）和ri分别表示视场内第i颗恒星的单位观测矢量和参考矢量，则三者满足如下关系：

图2 单颗导航星多曝光成像示意图Fig.2 Schematic diagram of multiexposure imaging of single guide star

式中：vi(t）和ri在星敏感器坐标系和天球坐标系下的表达式为

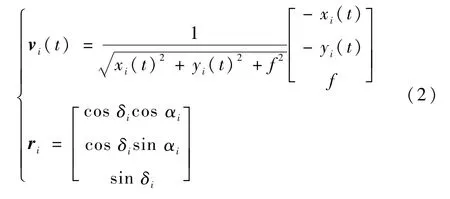
其中：(xi(t），yi(t））为第i颗导航星在像面上的成像星点的横纵坐标；f为星敏感器的焦距；(αi，δi）为第i颗导航星在天球坐标系下的赤经和赤纬。

如图2所示，在一个星敏感器工作周期内，第i颗恒星的成像星点自t0时刻位置运动至t1时刻位置，由式(1）可知：

由于参考矢量ri不随时间变化而发生改变，由式(3）可得

式中：A(t0）T为t0时刻星敏感器坐标系到天球坐标系的旋转矩阵；为星敏感器坐标系自t0时刻到t1时刻的转移矩阵。

当运动时间Δt＝t1－t0足够小时，转移矩阵近似满足如下表达式［15］：

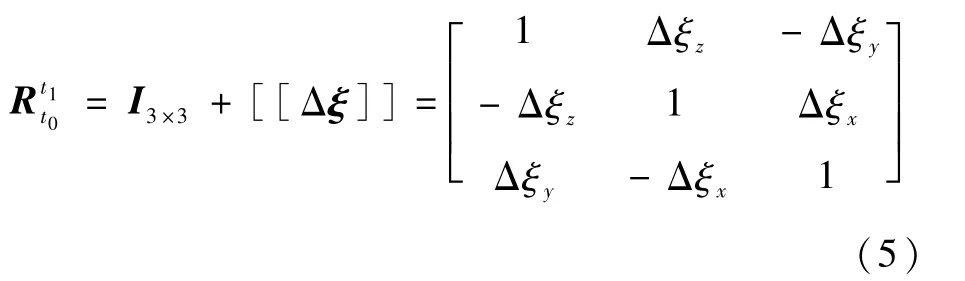
式中：I3×3为3×3单位矩阵；Δξ＝［ΔξxΔξyΔξz］T为运动时间Δt内的旋转角；［［Δξ］］为旋转角Δξ的反对称矩阵。

在较小的Δt时间内，对角速度变化情况进行一阶近似，其表达式为

式中：ω0＝［ωx(t0）ωy(t0）ωz(t0）］T和α0＝［αx(t0）αy(t0）αz(t0）］T分别为t0时刻的角速度和角加速度。

此时，由式(6）可得，旋转角Δξ的表达式为

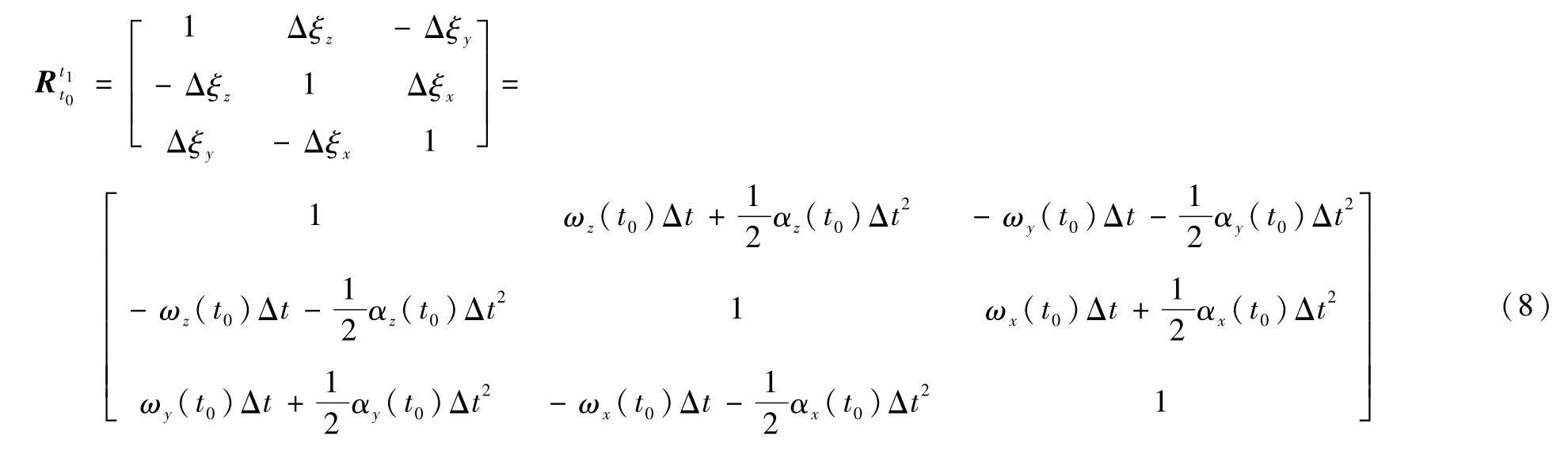
将式(2）和式(8）代入式(4），并考虑到焦距f是时不变的，则t0时刻和t1时刻对应的单位观测矢量之间关系的二维简化表达式为

式(9）中，根据星敏感器的参数进行计算可知，通常(－xi(t0）Δξy＋yi(t0）Δξx）／f＜0.01，相比于分母具有的常数项“1”可以忽略不计。因此，式(9）可以近似简化为

式(10）即为基于全运动参数的星点成像位置模型，表明了星敏感器在复杂运动条件下，t1时刻的星点成像位置坐标(xi(t1），yi(t1））由t0时刻的位置坐标(xi(t0），yi(t0））、焦距f、运动时间Δt及全运动参数(角速度ω0与角加速度α0）完全确定。

由式(10）可得，星敏感器工作周期(运动时间）Δt内，成像星点运动位移L表达式为

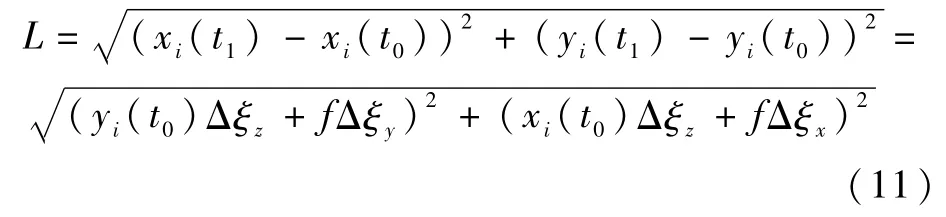
式(11）表明，星点运动位移L与全运动参数直接相关，星敏感器全运动参数越大，位移L越大，相邻星点轨迹相互交叉情况的发生概率越大，对多曝光成像方法性能影响越大。

3 全运动参数的仿真分析及优化

为了定量研究星敏感器全运动参数对星点轨迹交叉问题的影响，下面进行仿真分析。若星敏感器像面分辨率为A×A，工作周期Δt内星点运动位移为L，N(x）表示星点像面间距为x的星对数量，则相邻星对发生交叉的概率Po可以表示为

式(12）中，像面总长度A为常数，则相邻星对交叉概率Po由运动位移L确定，而由式(11）可知，运动位移L由星点初始位置坐标(xi(t0），yi(t0））、焦距f、工作周期Δt及全运动参数(角速度ω0与角加速度α0）完全确定。

式(11）中，考虑到初始位置坐标(xi(t0），yi(t0））与焦距f分别对视轴方向角位移Δξz与垂直视轴方向角位移Δξx、Δξy产生作用，为深入分析各自作用效果，下面分2类进行讨论。

3.1 垂直视轴方向

若星敏感器仅存在垂直视轴方向的角位移，则由式(11）可知，运动位移L仅与焦距f有关，而与初始位置坐标(xi(t0），yi(t0））无关。为简化运算，不妨假设星敏感器角速度ω＝［ωx0 0］T和角加速度α＝［αx0 0］T，则在不同焦距f下，当ωx或αx变化时，交叉概率Po的变化规律分别如图3和图4所示，仿真中涉及的其他参数如表1所示。图3、图4中，焦距f为42.78，31.94，25.40，21.02 mm时，对应的星敏感器视场大小分别为15°×15°，20°×20°，25°×25°，30°×30°。

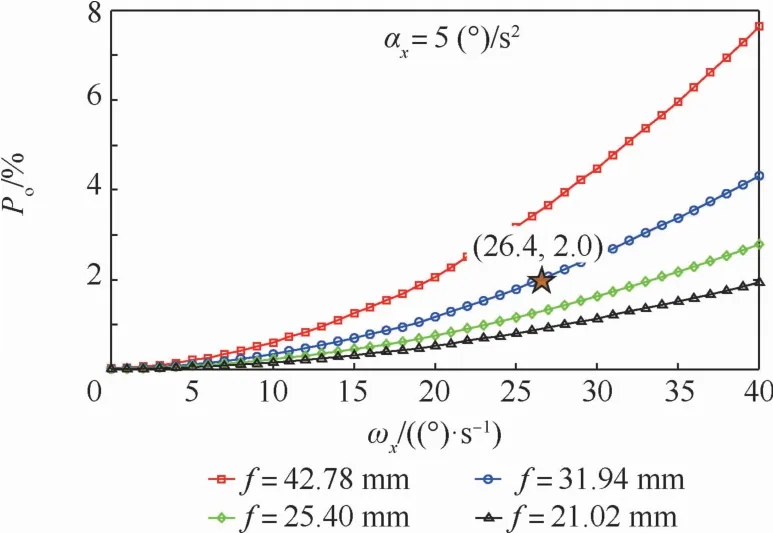
图3 交叉概率随角速度ωx变化Fig.3 Cross probability versus angular velocityωx

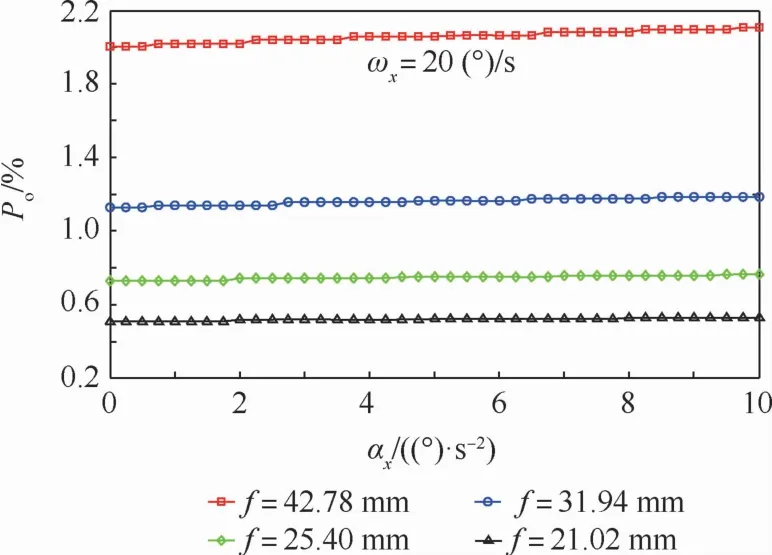
图4 交叉概率随角加速度αx变化Fig.4 Cross probability versus angular accelerationαx

表1 星敏感器部分仿真参数Table 1 Part of simulation parameters of star tracker

由图3可知，当固定角加速度大小αx＝5(°）／s2，角速度大小ωx由0(°）／s逐渐增大至40(°）／s时，交叉概率Po显著增大，同时，随着焦距增大，交叉概率Po同样逐渐增大。由图4可知，当固定角速度大小ωx＝20(°）／s，角加速度大小αx由0(°）／s2逐渐增大至10(°）／s2时，与图3相比，交叉概率Po变化较为缓慢，这是因为角加速度α通过工作周期Δt的平方影响角位移Δξ，α大小变化对Δξ影响不大；但是，随着焦距增大，交叉概率Po显著增大。需要注意的是，尽管焦距减小有利于交叉概率降低，但是焦距变化还会影响光学镜头的口径大小，若焦距过小，则会使得镜头口径减小，不利于收集微弱恒星信号，因此，最终选择f＝31.94 mm。

3.2 视轴方向

由式(11）可知，若星敏感器仅存在视轴方向的角位移Δξz，则运动位移L的表达式为

式中：rz为初始位置坐标(xi(t0），yi(t0））与坐标原点的距离。

由式(13）可知，此时L仅与初始位置坐标(xi(t0），yi(t0））有关，而与焦距f无关。

设星敏感器角速度ω＝［0 0 ωz］T和角加速度α＝［0 0 αz］T，则在不同距离rz像素下，当ωz或αz变化时，交叉概率Po的变化规律分别如图5和图6所示。

由图5和图6可知，交叉概率Po随着角速度ωz或角加速度αz的增大而增大；同时，Po还与星点初始位置有关，星点越靠近成像平面边缘，即距离rz越大，则交叉概率Po越大。

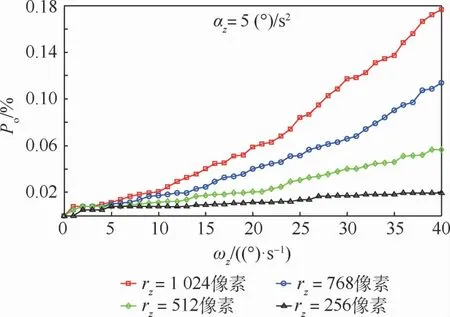
图5 交叉概率随角速度ωz变化Fig.5 Cross probability versus angular velocityωz

图6 交叉概率随角加速度αz变化Fig.6 Cross probability versus angular accelerationαz

对比图3、图4和图5、图6可知，交叉概率Po受到垂直视轴方向角速度、角加速度变化的影响比视轴方向角速度、角加速度变化的影响更为显著，前者的交叉概率Po比后者至少大一个数量级，因此，相比于垂直视轴方向影响，视轴方向对Po的影响可以忽略不计。考虑到工程实际应用，设定Po≤2%为星点不出现交叉情况的安全范围，则如图3所示，在角加速度大小为5(°）／s2情况下，确定角速度大小的极限安全值为26.4(°）／s。

4 外场观星实验

为了验证本文方法的有效性，进行了真实外场观星实验。图7为真实外场观星的实验装置示意图，图中实验装置主要包括多曝光星敏感器、便携式高精度转台及三角架等。多曝光星敏感器牢固安装在便携式高精度转台上，并随转台一起运动，转台的角速度与角加速度在理论仿真的极限安全值范围内变化(即角速度≤26.4(°）／s，角加速度≤5(°）／s2）。

图7 夜晚外场观星实验装置示意图Fig.7 Night star observation out-field experiment setup

实验拍摄了大量多曝光成像星图，任意选取其中2幅星图，如图8所示。图8(a）中，多曝光次数N＝3，图中共包含10颗导航星的全部3次曝光星点信息；图8(b）中，多曝光次数N＝5，图中共包含7颗导航星的全部5次曝光星点信息。上述星图中均未出现相邻星点轨迹交叉问题，因而不对多曝光成像性能产生影响。进一步，实验拍摄的大量多曝光成像星图，当星敏感器的角速度与角加速度在理论仿真的极限安全值范围内变化(即角速度≤26.4(°）／s，角加速度≤5(°）／s2）时，均未出现相邻星点轨迹交叉问题，表明相邻星点交叉情况为小概率事件(即满足Po≤2%），这与前述理论分析及仿真结果一致，从而验证了本文方法的有效性。

图8 不同多曝光次数的成像星图Fig.8 Star images with different multiexposure times

5 结论

1）在星敏感器全运动参数分析基础上，结合星敏感器的工作原理，对星点成像位置进行了建模。

2）根据星点成像位置模型，对交叉概率大小进行理论分析与数值仿真，仿真结果表明，在设定交叉概率不超过2%的安全范围下，角速度与角加速度的极限安全值分别为角速度≤26.4(°）／s，角加速度≤5(°）／s2。

3）外场观星实验结果与理论分析及数值仿真结果一致，验证了本文方法的有效性。