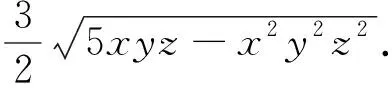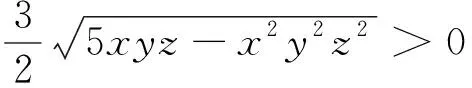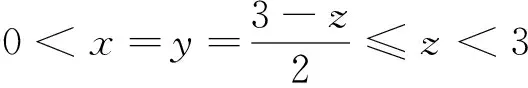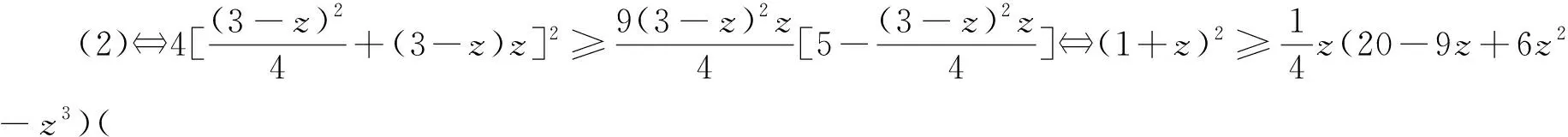一个不等式问题的另证

江苏省泰州市姜堰区南苑学校 (225500) 申才明

江苏省姜堰中等专业学校 (225500) 陈 宇

胡芳举老师在文[1]中介绍，本题由刘保乾老师提供，已经由机器给出了证明.胡老师通过构造函数，“用调整法”第一个给出人工证明.笔者在此将主要借助分析法给出该问题的一个另证.

⟺9x2y2z2+(xy+yz+zx)2-24xyz≥21xyz

⟺4(xy+yz+zx)2≥9xyz(5-xyz)≥0 (2).由于待证不等式两边循环对称，不妨设0

(ⅰ)当0

当λ=1时，即为原问题.