问渠哪得清如许，为有源头活水来——对2020年新高考山东卷第21题的思考

福建省福清第三中学 (350315) 何 灯

福建师范大学附属福清德旺中学 (350319) 周 宁

1.试题与解答

山东省作为新高考综合改革的先行省份，其命制的第一份新高考数学试卷引起社会广泛关注.其中，吸引笔者更多目光的是该卷的导数压轴题.

试题已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围.

试题第(2)问以学生熟悉的恒成立条件下求参数范围问题呈现，乍看平淡无奇，朴实无华，细细品味后却感觉内涵丰富，给人启迪.

对于含参函数试题，求解的通法是参数分离法或求导法.但该题包含了以e为底的指数函数和对数函数，因指数对数缠结，运用参数分离法求解无法分离出参数，运用导数法求解无法求出极值点，所以此类问题一般都是利用同构法予以求解.

所谓同构法，是指通过对不等式恒等变形，将其转化为形如F(g(x))≥F(h(x))(或F(g(x))>F(h(x)))的结构，利用导数研究F(x)的单调性予以求解的方法.下面是文[1]中利用同构法给出试题第(2)问的一个解答.

解析：由题意f(x)≥1恒成立等价于elna+x-1+lna+x-1≥x+lnx恒成立，等价于elna+x-1+lna+x-1≥elnx+lnx恒成立.令F(x)=ex+x，则F′(x)=ex+1>0，F(x)关于x在(-∞,+∞)上单调递增，从而elna+x-1+lna+x-1≥elnx+lnx恒成立等价于F(lna+x-1)≥F(lnx)恒成立，等价于lna+x-1≥lnx恒成立，即lna≥lnx-x+1恒成立.

2.分析与思考

3.启迪与简解

基于对数学美的感悟和启发，我们发现如果基于数学的结构美予以解答，问题可解决得更为直观简捷.

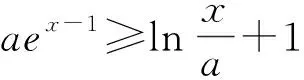
评注：上述解法的巧妙之处在于充分利用了表达式的结构特点和函数图像的特征，彰显了数学美在数学解题中的引领和指导作用.

4.体会和感悟

解题需要常规的固定模式，看到这道题，你的第一反应是什么？迅速生成常规方案，也即第一方案.因为80%的高考题是基本的、稳定的，处理难题，从方法论的角度讲就是转换视角.常态方案不行，就需换一个方案；这种说法与思路不通，就需换一个说法.但如何实现转换呢？如何把问题转换到我们熟悉的领域呢？这需要经验的积累，需要思想的立意，更需要数学美的启迪和引领.

教学中教师要不断创设数学美的认知活动，引领学生在数学的活动中感知数学美，体悟数学美，追寻数学美，应用数学美，让他们在美的熏陶洗礼中切实培养起数学的学习能力，发展起数学的核心素养.