基于灰色极限学习机的电机短路故障预测研究

周 克，王 霄，王 坤

(1. 茅台学院酿酒工程自动化系，贵州遵义564507；2.贵州大学电气工程学院，贵州贵阳550004)

1 引言

风力发电作为目前可再生能源发电的主要形式之一，由于技术和设施都较为成熟，因此得到了大力的推广和应用。然而风电机组的结构复杂、运行环境恶劣，使得发电机组的故障率居高不下，整个系统的维修成本也不断增加，尤其在海上风电场。在风力发电中使用最多的发电机为双馈异步发电机(Doubly fed Induction Generator， DFIG)，其常见的故障设备有发电机、齿轮箱和轴承等，其中轴承故障占40%、定子故障为38%、转子故障为10%、其它故障占12%[1]，现有的风力发电机故障的研究，多集中在故障的检测和诊断方面，属于事后维修，一旦事故发生，必然会导致机组停机，再次启动机组将耗费大量人力物力，如果采用预测的方式，配合日常的维护，将大大减少停机带来的损失。

目前，对于风电机组故障的预测方法主要是基于数据驱动的预测方法，该方法利用以往和现有的数据进行分析或构建模型来进行故障的预测。常用的方法有：神经网络[2]、支持向量机[3]和灰色理论[4]以及结合其它方法进行改进的一些预测方法：如将电流信号与振动信号结合，基于D-S证据融合理论建立的预测模型[5]；利用邓氏关联分析技术和数据融合方法改进的GM(1， n)预测模型[6]。这些方法通过采集风电机组的振动信号来进行分析，需要安装相应的测量传感器，配置数据采集系统，将对电机的运行状况产生影响，提高了故障预测的成本。相比于振动信号，风机的定子电流信号相对更为容易获取，而且电流信号中频谱所含信息更为丰富，频率、相位能反映出故障的性质，幅值则能够反映故障程度[7]。文献[8]利用定子电流分析法作为数据采集方案，对采集的电流信息进行高阶普分析，实现了风机的故障诊断，但高阶普的计算较为复杂，不适于快速大规模的工程应用。

针对现有故障诊断方法中存在的不足，本文引入一种融合灰色理论与ELM极限状态机的故障诊断方法，该方法利用灰色理论在处理波动性、信号不完整的优势，结合ELM神经网络的高线性映射特性，形成了一种运算速度快，泛化性能好转子的匝间短路故障解决方案。

2 匝间短路故障产生机理

风力发电机正常工作时，定、转子三相电流波形完全对称，幅值相等且相位互差120°，当有转子绕组发生匝间短路故障时，三相电流对称性将被破坏，不平衡的输出电流，会形成一电势差，该电势差的存在将形成一个与原磁场相反的旋转磁场，该磁场使得正常的圆形旋转气隙磁场变为椭圆形的旋转气隙磁场，变化后的磁场与定子绕组和转子绕组交链，进而在定、转子侧产生故障谐波分量，该谐波可表示为(1±2ks)f，k=1,2,3,…，其中f为定子侧额定频率，s为定子与转子的转差率。在发电系统中，转子侧与励磁系统相连，定子侧与电网相连进行馈电，所以，当发生转子匝间故障时，定子侧的电流谐波幅值变化将更加明显，更容易被采集观测。

针对转子的匝间故障问题，常见分析方法有基于电磁场有限元模型和多回路理论分析两种[9]，本文借助多回路理论进行分析：该方法将电机看作多个独立回路组成的电路网络，当转子绕组发生匝间短路故障时，将其作用等效为在短路匝增加一条故障回路，如图1所示的等效模型。当绕组AB段发生匝间短路故障，便可等效为在故障段AB上并联一个电阻Rf，故障的程度由被短路匝数与总匝间数比值μ表示。

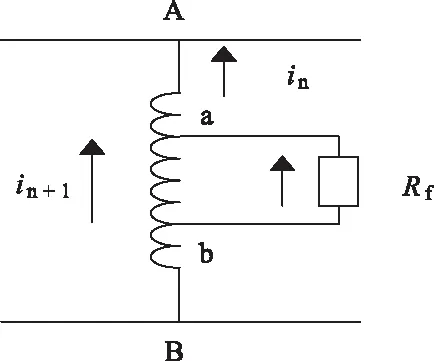
图1 多回路法等效示意图

3 灰色ELM预测模型

风电机运行的状况具有多变性，致使所采集到的电流参数呈现一定的随机性，此外，当发生匝间短路故障时，故障信号往往很微弱且容易被风机自身的电气信号所掩盖，故障样本数据量一般较少。灰色预测模型已被证明在处理数据量少、信息贫乏的问题时具有良好的性能，适合处理转子匝间短路的故障预测问题[4]。

灰色预测模型中，常用的模型有GM(1， 1)和GM(1， n)模型两大类，其中尤以GM(1， 1)模型使用最为广泛。该模型适用于数据量少、规律性较强且波动平滑的中短期数据预测，但是由于GM(1， 1)中求解参数时是利用最小均方差准则，因此输入信号间的映射关系得不到很好体现；ELM神经网络是一种具有高线性映射特性的算法，适用于数据量大和长期预测的场景。为充分挖掘上述两种算法的优势，本文引入ELM算法，作为GM(1， 1)模型的补充，同时，对传统ELM神经网络进行改进，解决了ELM神经网络训练时间过长的问题。预测模型如图2所示。

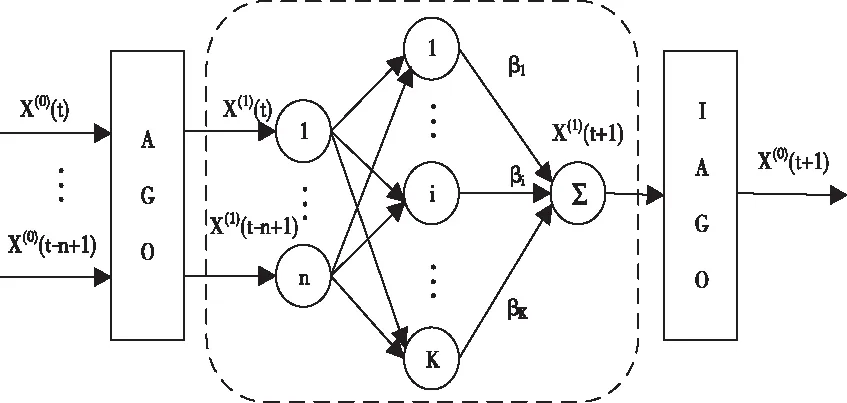
图2 灰色ELM预测模型

具体处理过程如下：

1)故障信号频域变换：提取故障时的定子电流信号，对该信号进行傅里叶变换，并利用RV窗函数对变换后的频谱进行提取，确保变换后频谱信息集中在窗口范围内，提高信号特征分辨率。能量RV窗函数的时域表达式为

n=0，1，2，…，N-1

(1)

其中，M表示窗函数项数，N为窗长，am满足公式

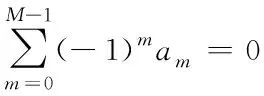
(2)

经过离散傅里叶变换，则有

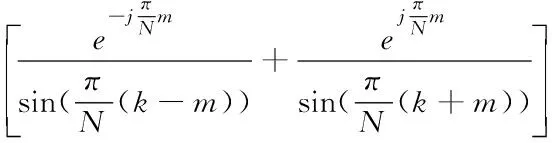
(3)

由于N远远大于1，于是可得

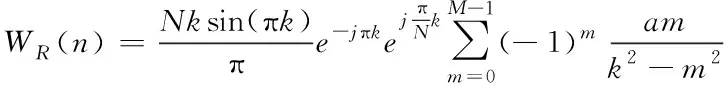
(4)

即得到RV窗h次谐波表达式

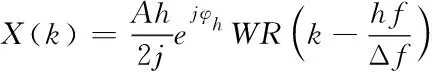
(5)

式中，f为基波频率。

2)灰色处理：利用式(6)将各故障频点处的幅值数据建立成新的数据序列，接着利用式(7)得到幅值序列的累加生成序列(1-AGO)，以弱化序列的随机波动性，挖掘出序列的深度规律。

设待处理数据序列为X(0)

X(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}

(6)

经过第一次累加生成得到其一次生成序列1-AGO序列

X(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}

(7)

x(0)(k)≥0，(k=1，2，…，n)

类似地，可得R-AGO序列

(8)

3)ELM神经网络训练：将式(7)中处理后的幅值序列作为ELM神经网络的训练输入数据。设定隐含层节点数K，随机生成输入权重ai和单元偏差bi，利用式(9)求出输出矩阵H。

H=(a1，…，aK，b1，…，bK，X1，…，XK)

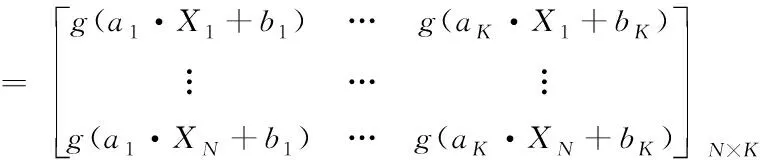
(9)

其中

β=[β1，β2，…，βK]K×m，T=[T1，T2，…，TN]N×m

此时，输出权值矩阵获得其最小二乘范数解便能得到，最小二乘范数解为

β=H+T

(10)

其中H+为隐含层输出矩阵H的广义逆矩阵。

4)ELM输出迭代：利用(10)式得到的输出结果，其精度受制于输入训练样本的个数以及样本的完整性，而实际发生故障时，样本训练数据是一个时间序列，有一定的先后顺序，因此，对原有输出数据可利用迭代算法进行更新，以提高输出数据的精度。

假设最初输入的训练样本向量为T0， 其对应隐含层输出矩阵为H0， 此时神经网络的输出向量为β0，此时满足：

β0=K0-1H0TT0

(11)

当后续新样本数据达到网络，根据一般递归最小二乘法与最小二乘解的更新的递归算法基本一致[10]，此时神经网络的输出可以利用式(12)进行更新计算。

βk+1=βk+Hk+1T(Tk+1-Hk+1βk)

(12)

此时，为了使迭代后的输出与原来模型的输出有同等的识别效果，此时在初始化数据时应该严格界定其数量，使H0的秩不小于隐含节点的数目。

在ELM神经网络模型的训练中，隐层节点的个数以及隐藏层激活函数的选取，关系到整个神经网络的执行效率和运算精度[11]，在本文的参数选取中，选取Sigmoid、Sin以及Hardlim三种激活函数进行性能测试，在测试基础上选择具有最佳性能输出的激活函数。

5)累减还原：将ELM神经网络的输出数据经GM(1， 1)的累减还原模块(IAGO)得到原始幅值的预测值(式(9))，将预测值减去最小值的绝对值，进而完成整个灰色ELM预测。

x′(0)(k+1)=x′(1)(k+1)-x′(1)(k)

(13)

整个算法如图3所示

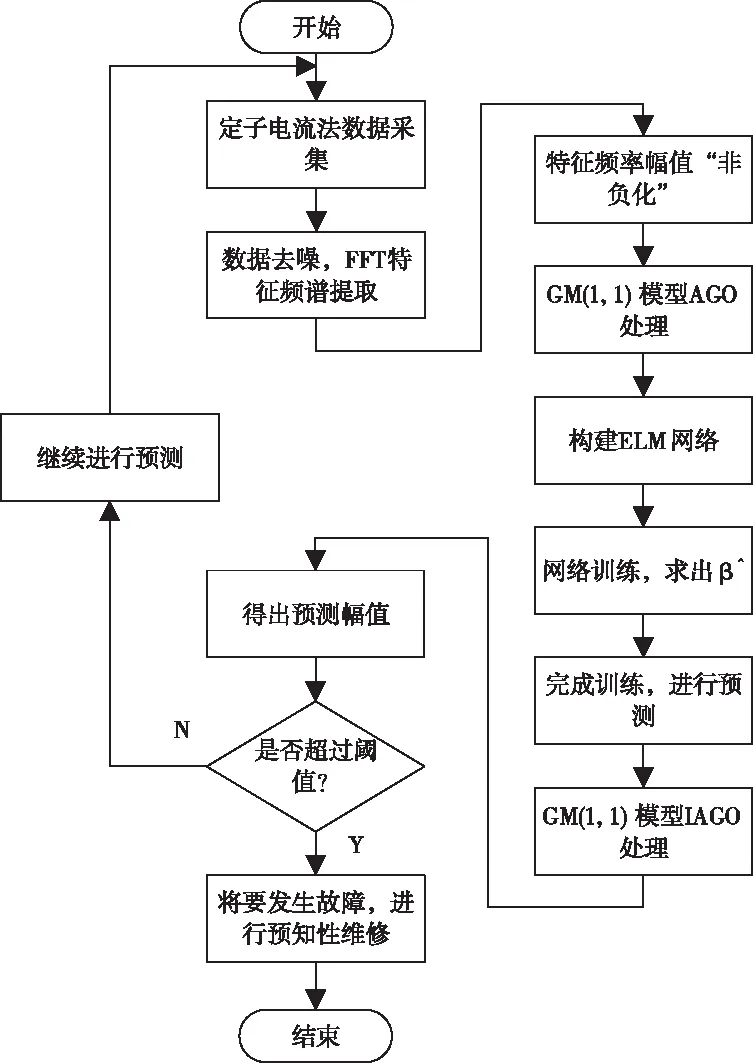
图3 预测模型流程图

4 模型仿真

为了验证本文所提方法的有效性，针对辖区内的多个风电场风机运行数据进行采集，选取发生故障时刻前后15分钟内的10台风机的定子电流数据作为实验数据，采样频率设置为T=500Hz。同时根据现场运行经验，对采集的异常数据进行筛除，最后将合格电流数据进行快速傅里叶变换，以提取特征频谱分量。图4，5为从某一风机故障数据的定子、转子波形图以及从该数据中提取的特征频谱图。

从图4中可以看出，当发生短路故障时，定、转子中的电流对称性被破坏，且定子电流中的非对称性表现更加明显，这符合本文的前述分析。通过对定子电流做傅里叶变换，通过加窗后得到的特征频谱如图5所示，从图中可以看出，会在定子电流中出现10 Hz、30 Hz、70 Hz、90 Hz、110 Hz、130 Hz、170 Hz等频率的谐波，且随着谐波次数的增加，谐波幅值呈现减小的趋势。这些特征频率处的幅值将是短路故障的判定依据。为了消除叠加在特征频率处的随机干扰，对这些特征信号做AGO处理，以便消除随机干扰。处理后的数据进行随机分组，构造ELM神经网络的训练集和测试集。

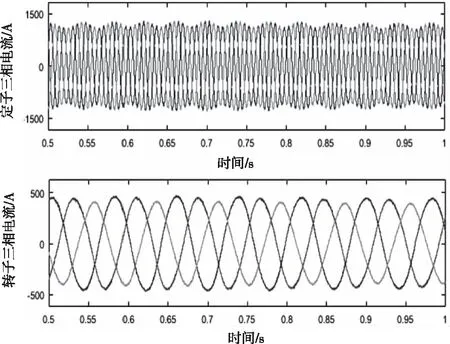
图4 故障时波形图

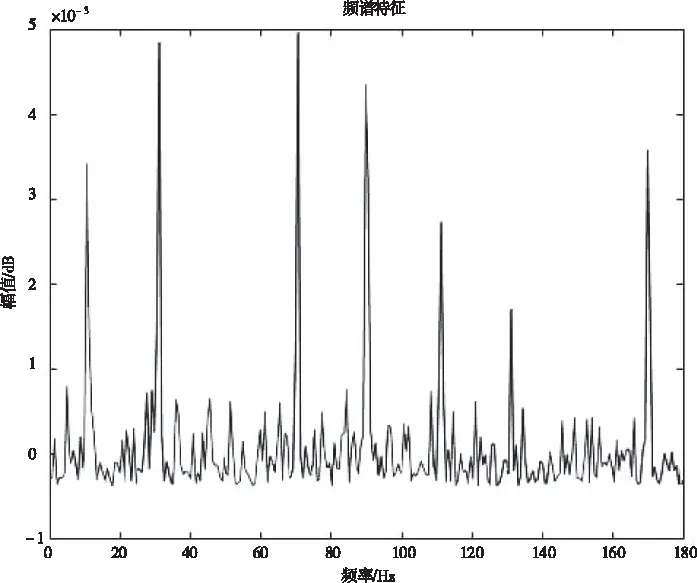
图5 故障数据中频率分量

虽然ELM神经网络通过随机分配输入权值和偏差，加快了ELM的算法速度，但过多的节点也会造成算法性能的下降，影响整个算法的运算效率。同时，在ELM中，激活函数可以帮助神经网络激活有用的信息，并抑制无关的数据点，但不同的激活函数在不同的输入数据和不同神经网络下，会表现出各自的优缺点。为了得到最佳的神经网络结构，本文对不同隐藏层节点、激活函数对预测的准确性做了比对实验，以求获得最佳参数设置。

由图6可知，在隐含层节点在50个左右时，模型准确率波动趋于稳定，模型准确率几乎保持在92%左右。由图7的不同激活函数对比可知，Sigmod函数的激活效果，Hardlim效果最差，且sigmod函数在历遍0到50的隐含层节点中，模型准确率一直保持在90%以上，且性能始终高于其它两类激活函数。根据对比实验结果，故选定激活函数为sigmod函数，输入层节点根据特征频点需要选择8个，隐含层节点N为50个，输出节点2个的ELM网络。

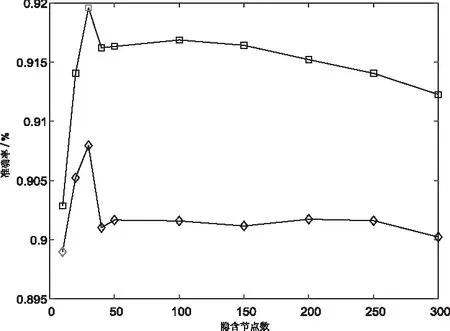
图6 隐含节点与准确率关系

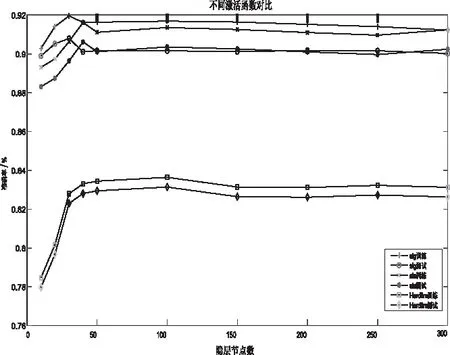
图7 不同激活函数与准确率对应图

为了衡量文章所提算法性能，文中使用均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)作为预测模型的优劣指数。指数的值越小，表明预测模型越理想。

计算公式如下

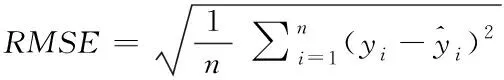
(14)

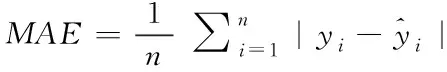
(15)

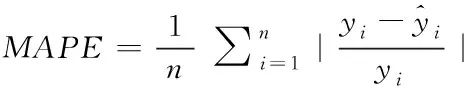
(16)

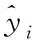
表1分别例举了使用相同的训练集与测试集数据，几种常用预测模型GM(1， 1)、ELM、灰色神经网络(GNN)和本文所提预测模型的性能对比。由表1可以看出，除了MAPE指标高于灰色神经网络(GNN)外，其余指标都要低于其它模型，而且相比较GNN预测模型，文中灰色ELM模型的耗时也有的减少。由于本文所提模型融合了GM(1，1)与ELM模型，因此在预测耗时上要比上述单独模型要长，对相较于融合两种模型的灰色神经网络，其耗时要短。由此说明，文章所提模型相较GM(1， 1)、ELM、灰色神经网络(GNN)，本模型准确率更高，模型具有很好的预测效果和精度，是一种有效的转子短路故障预测方法。

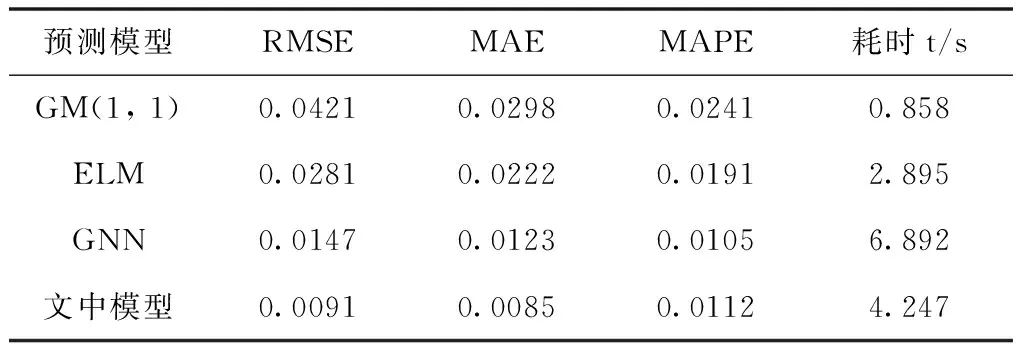
表1 GM(1， 1)、ELM、GNN和灰色ELM模型比较

5 结束语

文章针对风力发电机的转子匝间短路故障进行研究，提出一种融合GM(1， 1)模型与ELM神经网络相结合的模型，该模型即充分利用灰色模型对数据量要求低，对信号的随机变化不敏感以及较好的挖掘数据内部隐含规律特性，还充分利用了ELM神经网络学习速度快，预测精度高且不会陷入局部问题的能力，同时还利用递归算法对ELM神经网络训练过程进行改进，使其能更好适应时间序列输入信号的预测。在ELM神经网络的隐藏节点和激活函数的选择中，文章给出了不同参数时的系统的预测性能变化特点，依据变化特点选取了最优隐藏节点参数和激活函数，并将优化参数后的预测模型与GM(1， 1)、ELM、灰色神经网络(GNN)三种常用预测模型进行性能对比分析，分析结果表明，本文所提模型准确率更高，模型具有很好的预测效果和精度，是一种有效的转子短路故障预测方法。