一种改进加权函数的GCC时延估计方法研究

魏文亮，茅玉龙

(中国船舶重工集团公司第七二四研究所，江苏 南京 211106)

1 引言

在军事斗争领域，对敌方目标的定位主要有三种定位方法：有源定位、无源定位和利用第三方辐射源的无源相干定位。随着高灵敏度、高速信号截获和处理技术的发展，无源定位技术的研究和应用越来越广泛。它具有作用距离远，隐蔽性好等优点，因而具有极强的生存能力和反隐身能力。无源定位按照定位方法可以分为单站测向(DOA)和测相位差变化率定位、时差(TDOA)多站无源定位、差分多普勒定位、测向-时差联合无源定位等，其中时差多站无源定位以其较高的定位精度，较强的组网能力和抗打击能力等特点而应用更为广泛。

TDOA定位是无源定位技术发展的主要方向之一，通过测量辐射源信号到达不同观测站的时差构建时差观测方程，联立多个时差观测方程可计算出辐射源位置[1]。目前对TDOA定位的研究主要包括定位方程的解法算法、布站方式的选择和定位精度的分析，其中时差测量的精度是影响定位精度的一个重要因素，因此，对时差测量相关问题的研究十分重要。

目前，以下几种时差测量的方法较为常见：根据信号到达时间的测量时差法、广义互相关法[2-3](GCC)、循环互相关法[4]、广义双谱或高阶累积量[5]和自适应法[6]等，其中，最常见的是基于相关法的时差测量技术。基本相关法计算简单，但是如果观测站接收的信号信噪比较低，则不能获得良好的效果。为了降低或消除噪声对时差估计精度的影响，许多文献中提出了广义互相关(GCC)法的时差测量技术，通过信号处理中的互相关函数来估计信号的时差，对两个观测站接收信号的互功率谱密度函数进行加权滤波[7]。各种改进的方法主要是为了提高方法的抗噪声性能，增加其适用性。

使用传统的加权函数进行广义互相关时延估计，当信噪比较低时，通常会出现峰值拓展、多个峰值、小功率信号估计精度差等问题[8]，导致无法得到准确的时延估计效果，本文提出一种改进的加权函数，主要针对低信噪比下时延估计时出现信号的互相关函数峰值拓展、多个峰值以及小功率信号时延估计精度较差的情况进行改进。改进的加权函数可以很好地解决上述问题，提高时差测量的精度。

2 无源时差定位

2.1 时差定位基本原理

无源时差定位是利用主站和辅站之间接收到辐射源信号的到达时间差(TDOA)来定位的。获得时差的信息之后，通过乘以电磁波的传播速度就可以得到辐射源到主站和辅站的距离差，在二维平面中，就形成了一条以两站为焦点的双曲线，多个到达时间差的估计值就可以构成一组双曲面方程组。因此，二维时差定位至少需要三个观测站，而三维时差定位则至少需要四个观测站才能实现对目标的定位，其中包括一个主站(中心站)和三个辅站(边站)。如图1所示。

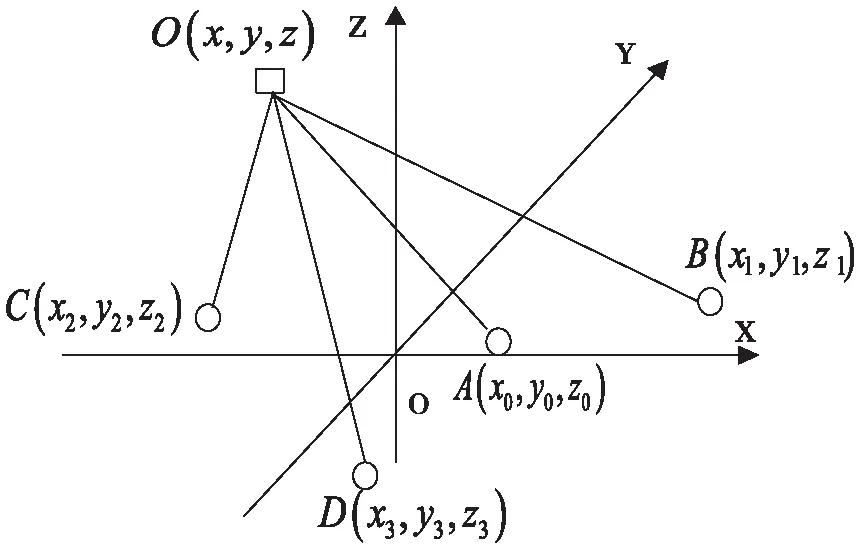
图1 四站三维无源时差定位模型

主站A的坐标为(x0，y0，z0)，辅站的坐标分别为B(x1，y1，z1)、C(x2，y2，z2)和D(x3，y3，z3)，辐射源O(x，y，z)，由图1的几何关系可以得到以下方程组：

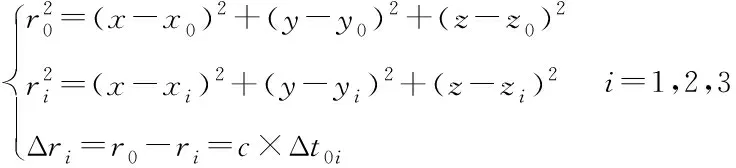
(1)

式中ri(i=0，1，2，3)表示辐射源到各站之间的距离：c为电磁波传播速度；Δt0i为主站与各辅站所对应的时差；Δri表示距离差。

2.2 时差定位算法

方程组(1)为一组关于目标辐射源坐标(xi，yi，zi)的非线性方程组，目前，有很多文献研究了关于这个方程组的解法，如Chan算法、泰勒级数展开法和其它一些算法等。

3 时差估计方法

3.1 基本相关法

基本相关法[9]是基于相关法进行所有时差估计的理论基础。

假设源信号为s(t)，主辅观测站接收系统接收的信号分别为x0(t)，xi(t)；噪声分别为n0(t)，ni(t)；信号的时延为di(t)；主辅观测站接收系统接收到的信号幅度分别为A0(t)，Ai(t)。主辅观测站接收系统接收到的信号模型为

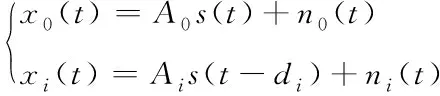
(2)

主辅观测站接收信号的相关函数为

Rx0xi(τ)

=E[x0(t)xi(t-τ)]

=E{[A0s(t)+n0(t)][Ais(t-di-τ)+ni(t-τ)]}

=A0AiRss(τ-di)+A0Rsni(τ)+AiRsn0(τ-di)+A0AiRn0ni(τ)

(3)

因为源信号、主辅观测站之间噪声无关，所以有

Rx0xi(τ)=A0AiRss(τ-di)

(4)

其中Rss(τ-di)为源信号的自相关函数，根据其性质可知，Rss(τ-di)≤Rss(0)。即当τ-di=0时，相关函数Rx0xi(τ)达到峰值[10]，主辅观测站接收到的信号的相关性最大，相关函数的峰值点即为时差估计的值。

3.2 广义互相关法

广义互相关法是基本相关法的改进，对其缺陷的克服，其原理就是在进行相关运算之前先对观测站接收到的信号进行滤波，适当消除噪声和干扰的影响，再进行相关运算，取其峰值进行时延估计，以达到提高时延估计精度的目的。

由Wiener-Khinchin定理可知，两路信号的互功率谱密度函数是其互相关函数的傅里叶变换[11]。则有

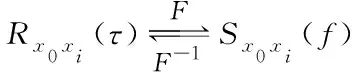
(5)

滤波器滤波之后的功率谱密度函数为

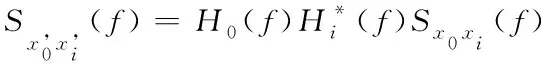
(6)

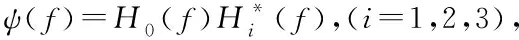
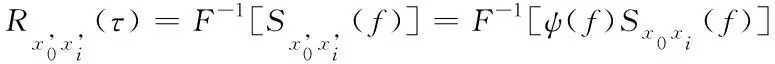
(7)

由此可见，广义互相关法实质是对功率谱密度函数作傅里叶逆变换之前先进行加权滤波处理，从而有效抑制噪声干扰的影响，然后会使得相关函数有一个峰值相对较大、较尖锐，其对应的横坐标即为时延估计值，从而提高时延估计的精度。

4 加权函数分析对比与改进

传统加权函数[12]如表1。

表1 加权函数

其中

|rx0xi(f)|2=|Sx0xi(f)|2/(Sx0x0(f)Sxixi(f))

(8)

基本互相关加权函数对外部噪声比较敏感，可能导致较大的时延估计误差，进而造成较大的定位误差；ROTH加权函数，可以有效地抑制噪声大的频带，具有一定的抗噪声性能，但容易拓宽相关函数的峰值，出现多峰值从而造成错误估计；SCOT加权函数，虽然考虑两个接收通道的影响，但当两个通道接收信号的功率谱密度相等时，也会拓宽相关函数的峰值，产生虚假的峰值造成错误估计；PHAT加权函数，与上述权值相比效果稍好，但因其加权函数分子始终是定常数，对于功率较大信号时延估计精度较高，而功率较小信号则会引入较大误差[13]。为改善以上传统加权函数时延估计的性能，本文提出一种改进的加权函数，为

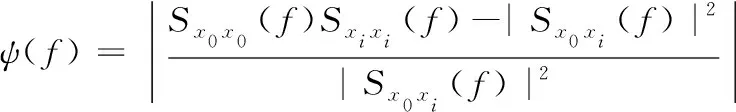
(9)

将式(9)带入式(7)，重新计算推导，得到

=F-1[ψ(f)Sx0xi(f)]

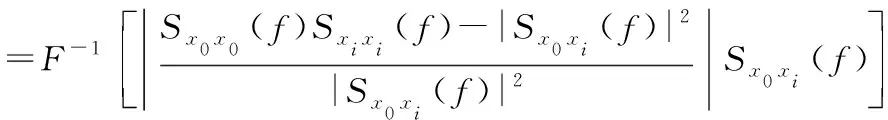
(10)

改进的加权函数，通过Sx0x0(f)Sxixi(f)兼容了SCOT加权函数的特性，克服了相关函数峰值拓宽而产生虚假峰值的影响；通过1/Sx0xi(f)抑制了较大的噪声频带。

ROTH加权函数仅采用一路信号的自功率谱密度函数加权，没有考虑两路信号的影响，相比较本文改进的加权函数兼顾考虑到两路信号同时会影响时延估计，在加权函数中同时采用两路信号的功率谱密度函数。相较于SCOT加权函数，本文改进的加权函数通过分母中的Sx0xi(f)来抑制相关函数峰值拓展而造成的多峰值现象。对于PHAT加权函数，本文改进的加权函数可以有效地改进PHAT加权函数在小功率信号下分母趋于零的现象，得到更高的时延估计精度。

考虑到加权函数的分母会随着信号功率的减小而减小，本文改进的加权函数，在其分子中同时加入两路信号的功率谱密度函数可以抑制分母减小时而出现较大的误差，同时分子也会随着信号功率的减小而逐渐减小，因此整个加权函数的误差可以逐渐减少，进而提高时延估计的精度。

本文改进的加权函数为了适用于不同功率的信号，在分子中加入了两路信号的自功率谱密度函数和互功率谱密度函数。应用于大功率信号时，兼顾了各加权函数的特性，以达到提高时延估计精度的目的；应用于小功率信号时，信号的自相关系数会随之减小，因此在小功率信号的情况下，改进的加权函数在分母逐渐减小的同时分子也在逐渐减小，进而达到提高时延估计的精度的效果。

5 仿真与分析

仿真分析的源信号选取雷达信号中的LFM信号，噪声选取非相关高斯白噪声[14]。主辅观测站接收信号的信噪比分别为SNR0和SNRi。信噪比(SNR)表达式为20log(σs/σn)，其中表示信号和噪声的标准差分别为σs，σn。假设噪声和源信号之间与噪声和噪声之间无关[15]。

实验分别仿真分析了基于各传统加权函数与改进加权函数的广义互相关法在不同信噪比下的时延估计精度，结果如图2、3、4所示；同时仿真分析了改进的加权函数对于小功率信号的时延估计精度，结果如图5所示；并对不同加权函数的时延估计进行100次仿真，采用均方根误差(RMSE)分析各加权函数的时延估计性能，结果如图6所示。均方根误差定义如下

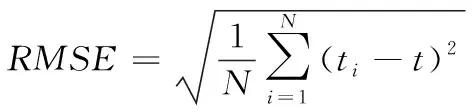
(11)

其中N为仿真次数，ti为时延估计值，t为时延真实值。

仿真参数设置如下：

脉宽：5μs

线性调频带宽：100MHz

采样频率：200MHz

数据点数：1000

预设时延：1us

1)信号幅度均取1时，各加权函数在不同信噪比下的时延估计精度

如图2、3、4所示，信号幅度均取1，当SNR=0dB时，不同加权函数的相关函数峰值尖锐明显，时延估计值均为1.005us，可以得到良好的时延估计精度。

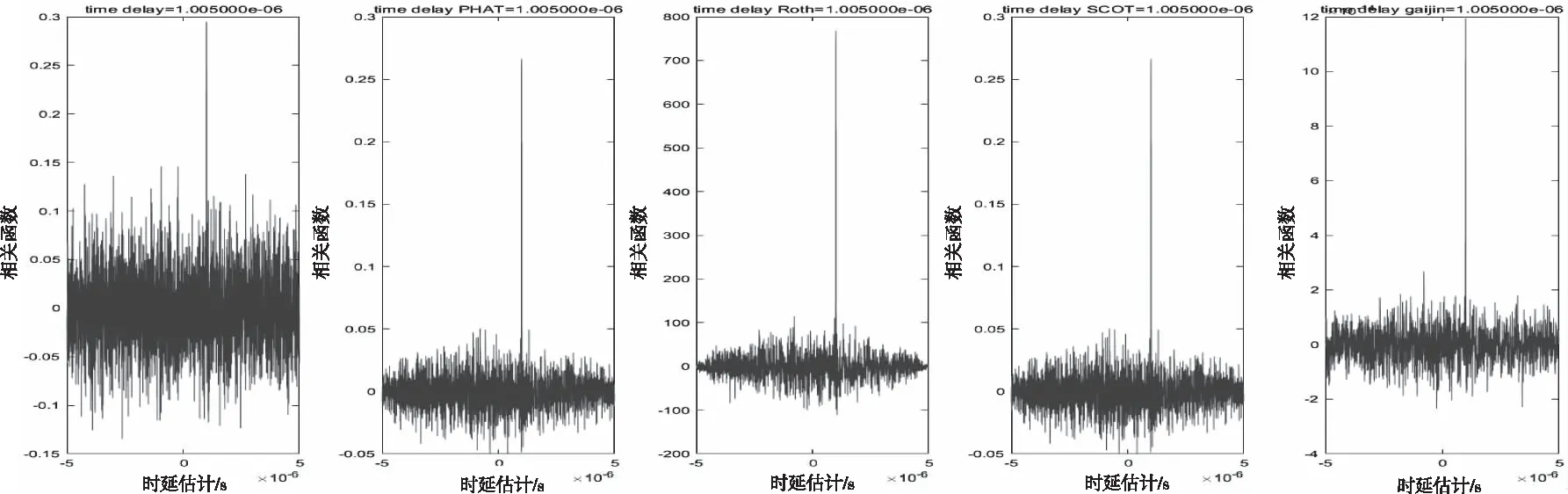
图2 SNR=0dB时各传统加权函数与改进的加权函数时延估计仿真

当SNR=-5dB时，不同加权函数的时延估计精度均受到了噪声的影响，其中基本互相关的相关函数已经出现多个峰值，无法准确进行时延估计。PHAT加权、ROTH加权、SCOT加权以及改进的加权函数的相关函数峰值仍然尖锐，时延估计值均为1.005us，具有良好的时延估计效果。

图3 SNR=-5dB时各传统加权函数与改进的加权函数时延估计仿真

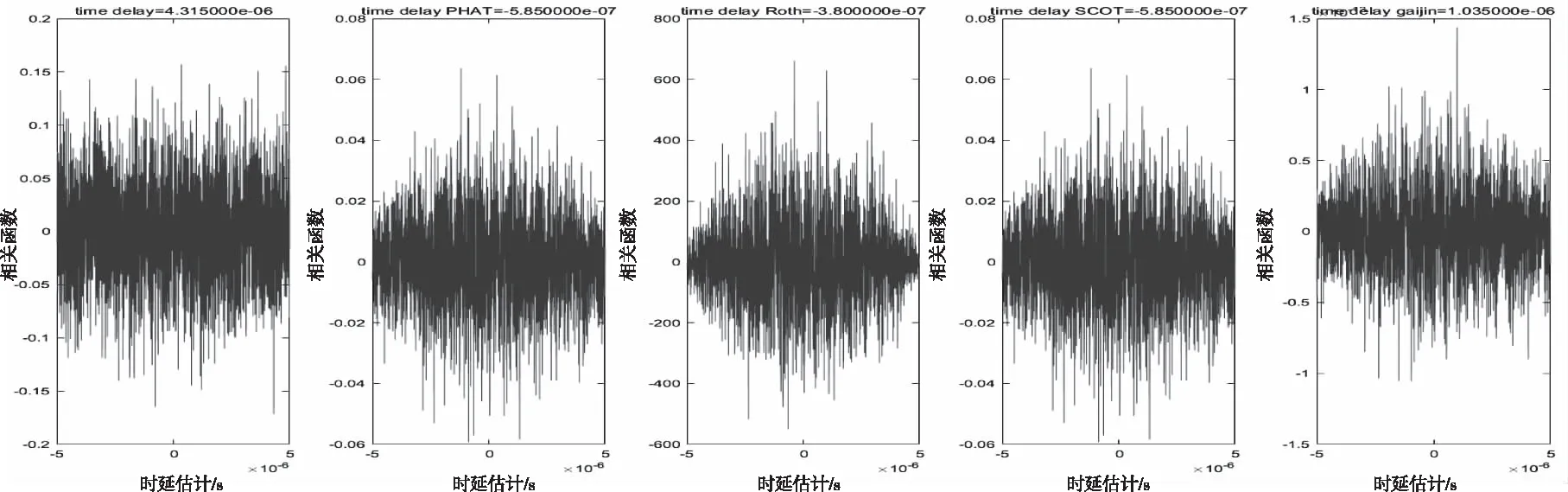
图4 SNR=-9dB各时传统加权函数与改进的加权函数时延估计仿真

当SNR=-9dB时，不同加权函数的时延估计精度均受到了较大影响，其中各传统加权函数的相关函数已经出现多个峰值，无法进行时延估计，而改进的加权函数虽然在一定程度上也受到较大干扰，但相关函数峰值尖锐程度仍然明显，时延估计值为1.035us，具有较高的时延估计精度。

随着信噪比的不断降低，各传统加权函数的相关函数峰值均无法准确分辨，而本文提出的改进的加权函数直到信噪比下降到SNR=-10dB时，才无法得到准确的时延估计，相较于其它传统加权函数具有更好的抗噪声性能。

2)信号幅度均取1e-7时，各加权函数在不同信噪比下的时延估计精度

如图5中所示，信号幅度均取1e-7，当SNR=0dB时，相比图2中信号幅度均取1时，各传统加权函数与改进的加权函数相关峰均尖锐明显，具有良好的时延估计效果。本实验中采用小功率信号时，各传统加权函数的相关函数峰值均已无法分辨，不能进行准确的时延估计，而改进的加权函数相关函数峰值尖锐明显，时延估计值为1.045us，对小功率信号仍然具有较好的时延估计效果。

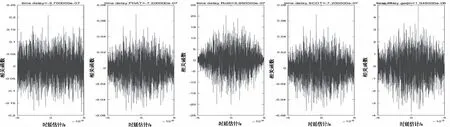
图5 传统加权函数、改进的加权函数时延估计仿真

随着信噪比的不断降低，对于小功率信号，本文提出的改进加权函数直到信噪比下降到SNR=-4dB时，才无法得到准确的时延估计，对于小功率信号相较于其它传统加权函数具有更好的抗噪声性能。

3)不同信噪比下各加权函数100次仿真分析

不同信噪比下对各加权函数进行100次仿真，均方根误差如图6所示，当信噪比降为0dB以下时，基本相关法已经无法进行准确的时延估计；当信噪比继续下降到-5dB以下时，各传统加权函数的时延估计精度急剧下降，逐渐无法获得准确的时延估计值；而本文提出的改进加权函数的广义互相关法仍然具有良好的时延估计精度，具有一定的抗噪声性能。

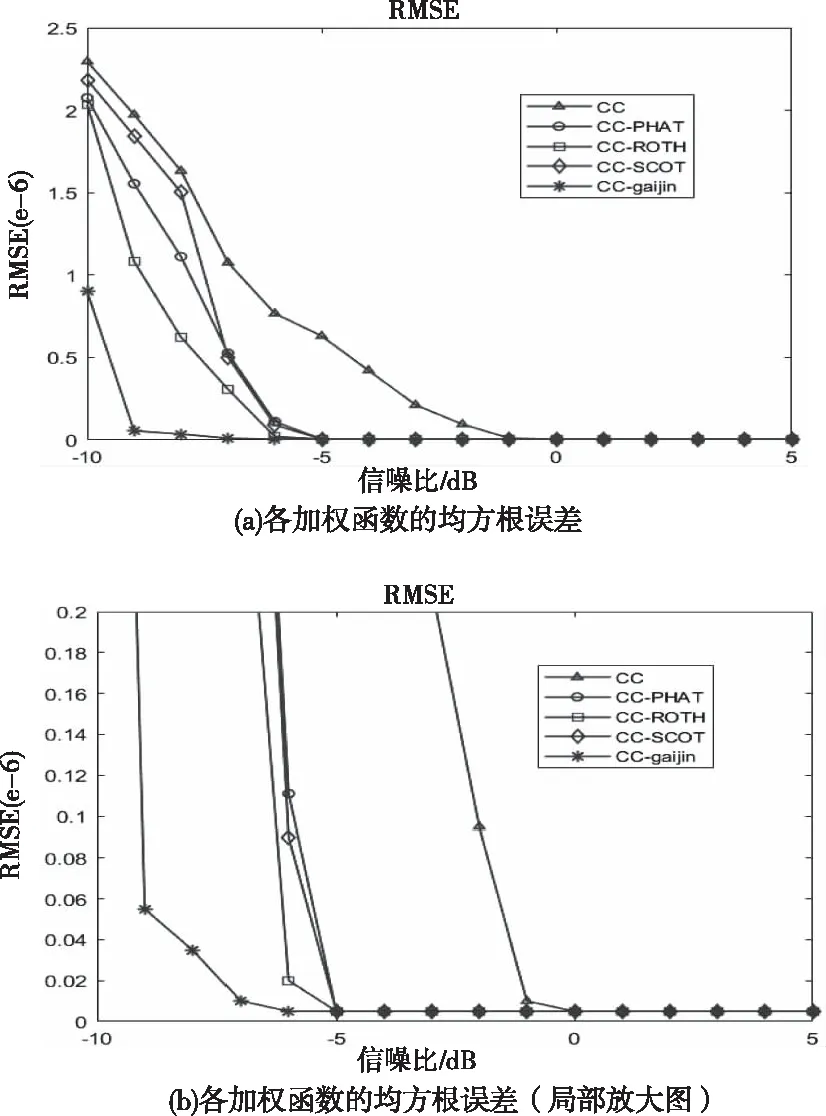
图6 各加权函数的均方根误差

6 结束语

本文提出一种改进加权函数的广义互相关时延估计方法，对其在不同信噪比下，对不同功率的信号重新加权仿真。当信噪比较高时，各加权函数的相关函数均可以观察到尖锐的相关峰，得到良好的时延估计精度。随着信噪比的不断下降，各传统加权函数的相关函数峰值均受到不同程度的影响，直至出现多个相关峰进而无法得到准确的时延估计，而改进加权函数的相关函数峰值尖锐明显，仍然可以得到准确的时延估计，具有较高的抗噪声性能。

对比图5和图2仿真结果，当信噪比相同时，对于小功率信号各基本加权函数均已无法分辨相关函数的相关峰，不能进行时延估计，而改进的加权函数对小功率信号的相关函数仿真仍然可以得到尖锐的相关峰，准确的进行时延估计。本文通过多次仿真和理论分析，表明基于改进加权函数的广义互相关时延估计方法对不同功率的信号都具有更好的抗噪声性能，具有一定的应用前景。