格栅式反推装置性能研究
杨 雄,梁 言
(中国飞行试验研究院,陕西 西安 710089)
1 引言
对于大型运输机,其传统着陆减速装置多为扰流板,车轮刹车装置或减速伞等,但随着运输机载荷不断增大,传统的减速制动装置已经难以满足目前高性能运输机的要求,因此以发动机反推系统为代表的新一代减速装置应运而生。相比于上述这些传统减速装置,反推减速装置可以显著缩短飞机着陆滑跑距离,并且其减速效率仅受到发动机工作状态的影响,不受跑道等外界场务因素[1][2],例如跑道湿滑程度的影响。除过可以在降落减速阶段可以投入使用,反推装置还可用于精确控制着陆,在飞行状态下开启用以减速,在起飞阶段进行中断起飞等。目前,反推装置几乎是先进大型运输机所必备的系统装置,随着我国各类型号的大型运输机的飞速发展,对反推装置及其反推性能的研究需求更加深入,因此需要积累在反推装置设计、研制工作的相关经验,推动在反推装置试验及鉴定领域的技术研究,以进一步支撑我国各重点型号大型运输机的研制工作。
国内、外目前针对反推系统的性能研究,主要的研究手段包括数值模拟手段和试验手段。试验手段主要包括台架试验,风洞试验和飞行试验,模拟手段主要包括参考发动机模型和CFD(Computational Fluid Dynamics)数值仿真。数值模拟手段是试验手段的重要补充,对于反推性能,目前主要采取参考发动机模型和CFD两种手段进行模拟。其中,参考发动机模型[3]可快速获得反推装置的反推性能,但其计算模拟需要风洞试验提供相关的参数与修正系数,同时,因参考发动机模型并不直接对反推流场进行仿真,故该手段无法准确获取反推装置的使用速度范围。随CFD技术的发展,基于CFD技术,对反推格栅、带反推构型的发动机整机及带反推短舱的飞机整机进行反推系统性能模拟成为可能,并且由于CFD仿真结果可为风洞试验的设计提供相关依据,因此基于CFD技术对反推装置进行性能模拟发展迅速。Strash等[4]在1997年采用全三维欧拉方程对某型商务机的蚌式反推构型进行了数值模拟,并与试验结果进行了对比,验证了数值模拟方法的可靠性;波音的Chen Chuck[5]在2001年采用全三维CFD技术对带反推构型及APU(Auxiliary Power Units)的典型双发商务机进行了数值仿真,研究了反推排气羽流与飞机外流场之间的气动干涉问题;Trapp等[6]在2003年对EMB170飞机的三种备选的格栅式反推结构进行了数值模拟,得到了不同的反推流场并进行了对比,同时模拟了反推开启时的飞机溅水试验,数值模拟结果与试验结果符合较好。国内方面,张国栋等[7]以二维格栅为研究对象,对其进行数值模拟,研究了主要几何参数对格栅排气性能的影响;周莉等[8]对CFM56-2发动机反推格栅的缩比模型进行二维数值模拟,研究得到了格栅安装角对反推装置性能的影响;吴宇等[9]对带反推构型的孤立发动机几何进行了全三维数值模拟,对反推性能全三维数值模拟的边界条件进行了相关研究;段卓毅等[10]采用全三维CFD方法对某尾吊双发布局飞机的反推装置性能进行了数值模拟,并重点研究了反推力装置与飞机之间的气动匹配问题;王志强等[11]在全三维环境下分别计算了单台发动机与飞/发一体化整机的反推流场,并评估了反推开启状态下反推气流对发动机进口流场的影响。
本文首先以带格栅式反推构型的波音767客机为研究对象,基于全三维CFD数值模拟技术,计算得到不同着陆滑跑速度下的整机外流场。通过对比反推模式各关键截面动量推力与GasTurb中动量推力,定性验证CFD模拟结果的正确性。在流场计算结果的基础上,计算得到发动机反推系统的总反推力、反推效率等反推性能;之后,基于飞机滑跑过程的运动学方程,建立起反推打开构型下飞机着陆性能计算方法,计算得到飞机的着陆滑跑时间及滑跑距离等着陆性能,通过对比该型飞机公开的着陆性能,验证所建立着陆性能计算方法的正确性和有效性。
2 整机安装条件下反推装置性能计算
本文以发动机反推装置展开时的波音767-400客机为研究对象,采用全三维CFD技术,对该飞机着陆滑跑时反推展开的外流场进行数值模拟,根据数值模拟结果,从流场结果中提取相关气动参数,计算得到该型飞机反推装置的性能。
2.1 整机全三维计算域及网格划分
计算域宽度为飞机半翼展的2倍,计算域底部确定为飞机着陆滑跑时跑道距机身底部的真实距离,计算域顶部距上机身距离确定为1倍机翼长度。
进行数值计算前,对计算域进行流场网格划分。采用非结构化网格进行计算域网格划分,总网格量约1000万,飞机近壁面附近生成边界层网格,边界层最大厚度最大指定为1e-5。网格划分结果如图1所示。
2.2 计算边界条件给定
对于飞机外流场区域,本文所选取的边界条件如图2所示。计算域进口为速度进口,根据不同的飞机滑跑速度,给定边界进口速度以模拟远场来流;计算域出口选为压力出口;飞机半模内侧面以及计算域顶部边界面选为对称边界;地面选为滑移边界,运动速度与飞机滑跑速度相反,以模拟移动地面,整个飞机外壳避免选定为无滑移壁面。

图2 外流场计算域边界条件
对于反推装置,本文给定的边界条件如图3所示。给定发动机进口,格栅出口和发动机内涵出口处的边界条件。其中,发动机进口确定为压力出口边界,给定该截面的静压;内涵出口和格栅出口确定为流量进口边界,给定上述两个截面位置的总温,总压和气流角。格栅出口截面的气流角由参考文献[12]取得。
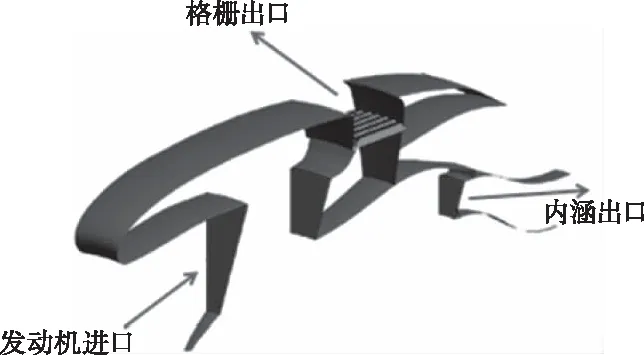
图3 发动机反推装置边界条件
2.3 数值模拟方法
本文采用Fluent进行整机流场的全三维数值模拟,对全计算域求解RANS方程。选用耦合式求解器,采用二阶迎风格式离散控制方程,求解算法采用SIMPLE算法。湍流模型选定为双方程k-ε模型。
2.4 数值模拟结果及分析
根据大多数反推装置实际的开启和关闭时飞机的滑跑速度,本文对飞机滑跑速度为160节,100节,40节和10节共4个工况下的反推开启时整机的外流场进行了数值模拟,得到上述4个工况下反推装置附近的流线图如图4所示。
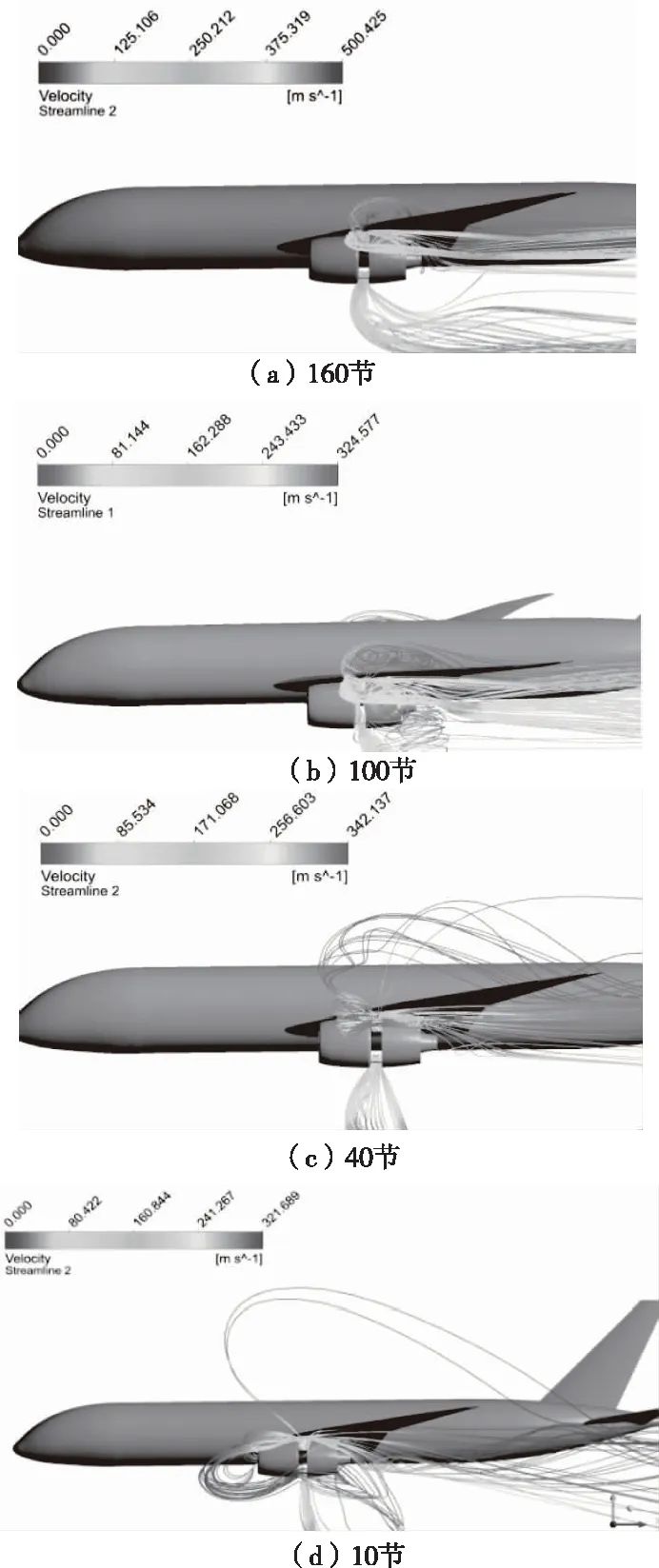
图4 四个工况下反推装置附近的流线图
由图4可知,反推排气气流从反推格栅出口流出后,在高速来流情况下(160节~40节),向后流动。靠近飞机机翼部分的反推排气气流在高速来流的影响下,向后流动,绕过飞机上翼面,且随着来流速度降低,绕过上翼面的气流逐渐形成半径较大的涡旋状流动结构。当来流速度降低至40节时,反推气流已经出现向滑跑速度方向前倾的趋势,当来流速度降低至10节时,由于来流速度过低,反推气流向前流动效应强烈,导致格栅的反推气流被吸入发动机进气道,造成二次吸入现象。
图5给出了上述4个工况下,反推装置附近的温度等值面图。由图可以看出,在高速工况下(160节~40节),经反推格栅排出的反推气流全部向飞机尾部流动,随着来流速度的逐渐降低,与图4所示流线图类似,反推气流在飞机上翼面逐渐形成半径较大的涡旋状温度等值面,其等值面开始向机头前方倾斜。当来流速度降低至10节时,排气格栅的流体温度场延伸发展至进气道,造成发动机反推排气尾流的二次吸入。

图5 四个工况下反推装置附近的温度等值面图
2.5 数值模拟结果的验证
由于缺乏该型发动机安装反推力的试验数据,可通过对比CFD反推模式下与GasTurb在正推模式下发动机各关键截面出的动量推力,来定性判断CFD计算结果的合理性与可靠性。本文在进行CFD计算结果合理性分析时,采用的基本假设为反推作用的有效面积与正推模式下涵道喷管的有效面积比接近于1。可以预见,在上述假设下,若发动机进口动量推力和内涵出口动量推力基本相等,反推模式下格栅出口动量推力略小于正推模式下外涵出口动量推力,则表明反推的CFD计算结果基本合理。表1给出了采用GasTurb计算得到的该发动机正推条件下的内、外涵道动量推力结果,同时给出了采用CFD手段获得的各反推正常工作的工况下,内、外涵的动量推力计算结果。通过对比可以看出,对于发动机进口和内涵出口,两种手段获得的动量推力结果基本相当,而对于外涵出口,反推模式的计算结果略低于正推模式的计算结果,这是由于反推模式下外涵出口气流还需经过反推格栅,从而造成了相应的动量损失。

表1 GasTurb计算动量推力与CFD计算值对比
2.6 反推装置性能计算
本文根据SAE AIR 6064中推荐的反推装置总反推力及反推效率的计算方法,基于本文所取得的CFD流场模拟结果,整理得到反推装置装机条件下的反推性能。计算反推性能时,根据相关适航条款中对反推装置开启和关闭速度的考核规定,只计算滑跑速度为60节~160节时的反推性能。其中,总反推力的计算方法如下
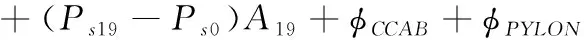
(1)
反推效率的计算方法如下
ηrev=FA/FG
FA=Frev+Fcore
(2)
FG=Ffan+Fcore
根据CFD模拟结果,按照式(1)及式(2),提取流场中的推力分量及阻力分量,进而得到装机条件下的反推性能如表2所示。

表2 反推性能计算结果
3 反推装置开启条件下飞机着陆性能计算方法
在获得反推装置性能的基础上,结合飞机的近地升阻特性,建立飞机着陆过程运动学方程,从而计算得到反推开启状态下飞机反推装置运行的时间以及飞机的着陆滑跑距离,将获得的飞机着陆性能与飞机公开的着陆性能对比,验证所建立着陆性能计算方法的可靠性和有效性。
3.1 反推工作时间的计算
对于大涵道比分排涡扇发动机,反推开启时发动机的受力分析如图6所示。

图6 反推开启时发动机短舱控制体受力分析
对发动机短舱所形成的控制体,其净推力可表示为如下形式
F=mfanVjsinβ+maV+mcoreVcore
(3)
式中,mfan为外涵道空气流量,Vj为反推排气气流速度,β为反推排气气流角度,ma为发动机进气流量,V为飞机滑跑速度,mcore为发动机内涵空气流量,Vcore为发动机内涵排气速度。对整个飞机,在反推打开时的减速阶段,其运动学方程如下

(4)
式中,m为飞机着陆质量,n为飞机所配发动机个数,Dav为减速阶段飞机的平均阻力。式(4)为一个一阶常微分方程,其通解为
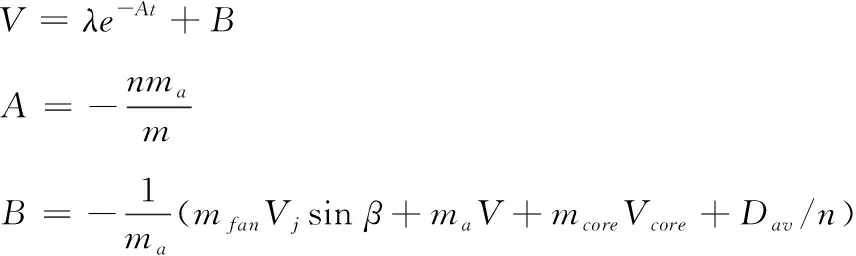
(5)
将t=0时刻,飞机着陆接地速度V0带入通解式(5),得到系数λ,进而由式(5)可解出反推开启状态下,飞机从接地速度V0滑跑至任意速度V时的滑跑时间t如下

(6)
实际采用式(6)计算反推运行时间时,可先求反推装置各块格栅的反推动量,进而求各格栅反推动量推力之和,从而求出式(6)中总反推动量推力。这一过程如式(7)所示

(7)
根据本文计算得到的反推装置性能结果以及上述飞机着陆过程的运动学方程,本文计算了从飞机接地反推装置开启(140节)到反推装置关闭(60节)过程中反推运行时间,如表3所示。

表3 着陆阶段反推装置运行时间
3.2 着陆过程滑跑距离的计算
将飞机接地后的着陆滑跑过程分为三个阶段,分别为从接地到反推开启的反应阶段,反推运行时的减速滑跑阶段以及反推关闭后的减速滑跑阶段。反推开启的反应阶段,飞行员从接地到开启反推,一般需要2~3秒,假设该阶段飞机作匀速运动。反推运行时的滑跑阶段和反推关闭后的减速滑跑阶段可视为匀减速运动过程,故三个阶段的滑跑距离计算式如下所示
S1=tVtd
(8)
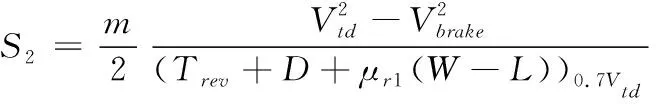
(9)

(10)
在第二阶段,飞机运动速度较高,故以0.7倍的接地速度计算飞机阻力及地面摩擦力,第三阶段飞机速度较低,以0.35倍接地速度计算飞机阻力及地面摩擦力。上式中第二阶段,飞机轮胎尚处于滚动摩擦阶段,滚动摩擦系数μr1视跑道状况取0.01~0.04,第三阶段飞行员关闭反推系统,发动机放慢车状态,采取机械刹车的方式,飞机轮胎多处于滑动摩擦阶段,滑动摩擦系数μr2视跑道状况取0.5~0.7,第三阶段飞行员关闭反推时的飞机速度Vbrake一般取0.3~0.5Vtd。
根据本文计算得到的反推力性能以及采用GasTurb计算得到的该发动机慢车推力,计算得到飞机以140Kn速度接地时飞机的着陆距离,如表4所示。

表4 着陆阶段滑跑距离
由表4可以看出,反推开启后,在干跑道上的着陆滑跑距离缩短了约4%。这与大部分民航客机在干跑道上采用反推装置所取得的效果较为一致,民航客机采用反推装置,在干跑道上仅缩短着陆滑跑距离的0-7%。在干跑道使用反推装置的主要目的,是减少刹车装置的磨损,因此并不能显著缩短滑跑距离。上述计算结果可以一定程度上说明本文所建立的反推开启状态下飞机着陆性能计算方法的可靠性。
4 结论
本文采用全三维数值模拟技术,研究了整机安装状态下格栅式反推系统性能计算方法;在此基础上,进一步研究了反推展开情况下的飞机着陆性能,得到结论如下:
1)该飞机反推装置在着陆速度140节~60节速度范围内反推装置可正常工作,未见反推气流二次吸入;反推装置工作期间,单发净反推力范围为151kN~113kN,总反推效率在各速度下接近40%;在滑行速度为13节时产生较为明显的发动机反推气流二次吸入现象;
2)反推打开情况下飞机在干跑道上的着陆性能计算结果表明,飞机着陆期间反推工作时间为29.64s,滑跑距离为1337.26m,相比于反推不打开情况下的着陆滑跑距离,缩短约4%,这与大部分民航客机在干跑道上采用反推装置平均缩短滑跑距离约0~7%的效果较为一致;
3)上述计算结果表明,本文所建立的反推性能计算方法和飞机性能计算方法,所获取的结果与实际情况较为符合,表明上述方法较为可靠,具备一定工程实用价值。

