新型动态变弧长模型在接地弧光中的应用研究

曾 晗，王利娜，林文萱，赵 帅

(华东交通大学电气与自动化工程学院，江西 南昌 330013)

1 引言

配电网作为电力系统的终端，具有结构复杂、接地故障频发、对地参数及故障参数变化范围广和运行状态及故障状态难以预测等特点。多年来，对配电网接地故障及过电压的快速处理和有效抑制仍未有较全面的解决方案[1][2]。

在电力系统中，为了正常运行与工作的需要，通常需要将系统的中性点与大地之间进行连接。配电系统中约85%以上的故障为单相接地故障[3](Sigle-line-to-ground ， SLG)。因此，对系统中性点连接方式一般是按系统发生SLG短路故障时故障电流大小进行分类：小电流接地系统和大电流接地系统。现如今在中国35kV及以下电压等级的配网多为小电流接地系统。

有学者认为，在以架空线路为主的配电网中，采用小电阻接地方式并不是明智之选，因为这类配电网接地次数较为频繁，采取小电阻接地方式会显著增大跳闸率[9]。而采用经消弧线圈补偿的小电流接地方式则可对故障电流进行补偿[10]，使得接地电弧易于熄弧，可实际应用中消弧线圈的问题也非常突出，传统消弧线圈无法补偿故障残流中的谐波及高频分量，这会使SLG故障时电弧难以自熄，无法实现消弧。

还有部分学者认为，由于目前城市配网电缆化率的提高[6]，发生SLG故障时，流过接地点的电流显著增大，且电缆故障多为永久性故障，建议在配网中使用小电阻接地方式[7]。该方式虽然对弧光接地过电压起到良好的抑制作用，提高了故障选线的准确率[8]。但其切除故障线路的方式大大降低了系统供电可靠性，故障点的大电流也可能扩大事故范围，引发安全问题。

而在对小电流接地系统中性点接地方式的研究中，有些学者认为可以采用中性点不接地方式[4]，该方式运行简单，中性点位移电压小，但是发生SLG故障时，无法实现自我熄弧[5]，会引发严重的事故，无法保证电力系统的供电可靠性与安全性，现我国中低压配网多数使用的仍为中性点不接地系统[17]。

综上所述在各类型的研究中配电网SLG的仿真模型都必不可少，但上述文献未对SLG故障中电弧的数学模型中关键参数的设计进行深入的分析和讨论。因此本文以小电流接地系统为背景，在Cassie-Mayr经典电弧模型的基础上，考虑了弧隙能量平衡原理对该模型在弧长变化下的影响，在模型的推导过程中改进了相关参数选取，研究弧长对电弧模型的影响，提出了一种综合接地电弧模型。将综合动态模型应用到整个配网当中，区分电缆、架空、混合线路在电弧模型中的差异，通过模拟间歇性弧光接地故障的电弧燃烧过程，来验证该电弧模型的正确性。

2 综合动态电弧模型的建立

Mayr电弧模型的方程为

(1)

式中：gm为Mayr模型的动态电导；Tm为电弧时间常数；E为弧柱的电场强度；i为电弧电流；Ploss为电弧燃烧时的逸散功率。

Cassie电弧模型的方程为

(2)

式中：gc为Cassie模型的动态电导；Tc为电弧时间常数；us为电弧的电压梯度；u为电弧瞬时电压。

在电弧燃烧过程中，传统单一模型描述电弧均存在缺陷，为提高电弧模型准确度，现将两者特点结合，形成综合动态模型，其计算过程如图1所示。在电弧电流较小接近零点时，Mayr电弧模型起主导作用，随着电流的增大，Cassie模型起主导作用[15]。

图1 综合动态模型计算过程

本文综合考虑弧长变量因素对电弧时间常数和电弧稳态电导常量的影响，将式(1)和(2)中电弧时间常数Tp表示为电弧电压的上升速率

(3)

式(3)中ϖ为常数，由经验值[6]取2.85×10-5；Ip可近似采用直接接地时的短路电流；Lp为电弧长度。

Gp为电弧稳态电导常量，其物理意义为恒定外界条件时，维持电弧燃烧的电弧导值，可表示为

(4)

式中|i|为一次电弧电流的绝对值；EP为单位长度的静态电弧压降。

us=EpLp

(5)

Ep为电弧的电压梯度，由文献[14]可知，沿着主电弧柱的电压降基本与电流无关，对于大部分的电弧周期，每单位长度固定电弧电压降基本为定值，所以取Ep=15V/cm。

3 电弧仿真模型

3.1 SLG故障综合仿真模型

在ATP/EMTP中建立如图2所示的SLG故障综合动态模型。模型参数为：电源电压u=10kV，频率f=50Hz，线路长度为10km，线路参数为：r=0.45Ω/km，L=0.9337mH/km，C=0.7074pF/ km。Mayr模型参数：Tm=0.3μs，Ip=140A；Cassie模型参数：Tc=1.2μs，uc=3.85kV，电弧压降Vp=15V/cm，仿真步长为2μs。

图2 综合型模型仿真图

电弧模型电压波形输出如图3所示，电弧电压畸变比较严重，其波形均类似于“马鞍”型。Cassie模型要比Mayr模型的过电压尖峰更陡峭，畸变更加严重，但两者均未有明显的燃弧电压和熄弧电压，相对比综合动态模型电弧电压波形，有明显的燃弧电压和熄弧电压，可以更好的反映实际电弧特性。

图3 传统模型与综合模型电压输出波形对比

如图4所示的电弧电流波形可知，在起始燃弧时刻，电弧电流过零点后，呈现高阻特性，电阻值达到最大，有明显的尖峰突起，此时有电流“零休”特性，之后电流逐渐增大，在电弧趋于稳定时，电弧电流近似于正弦波。对比综合动态模型电弧电流波形，有较明显的零休时间，约为1.6ms，可以更好的反映实际电弧特性。综合动态模型的电压和电流波形与文献[16]中电弧电压、电流实验波形基本一致，可知电弧的特性能够很好的体现在综合动态模型中。

图4 传统模型与综合模型电流输出波形对比

但不同的电弧长度和时间常数的设置，也会影响电弧电流的“零休”特性，本文将不同弧长变量下的电流波形进行对比如图5所示。然后记录不同弧长参数下电弧仿真结果如表1所示。

表1 不同弧长参数下电弧仿真结果

图5 弧长综合电弧模型电流波形对比

如图5所示，在弧长为50cm时，电弧电流的零休状态并不显著，在弧长大于80cm时，出现明显的零休时间，重复多组试验结果对比可得：随着电弧长度Lp的增大，稳态电弧电导Gp逐渐减小，对应的电弧电压增大，电弧电流出现零休状态更加显著，电弧电阻值增大，此时电弧逸散功率随弧长增大而增大，储存在弧柱的能量减小，使电弧在电流过零时更易熄灭。

3.2 配网间歇性弧光接地故障仿真模型

将单相接地故障电弧模型应用到整个配网中，在发生A相接地故障时，故障相和非故障相的电压电流如图6所示，由图可知中性点的电流畸变严重，而故障时最易造成间歇性弧光电弧，不仅会引起设备过电压，还会导致电网故障。

图6 配网SLG故障三相电压电流波形图

电缆线路以运行故障率低、供电可靠性高、占地面积小等特点逐渐取代架空线路，现成为智能配网中的主要线路形式[19]。为反应实际配网中各线路结构成分，配网模型设置如图7所示。

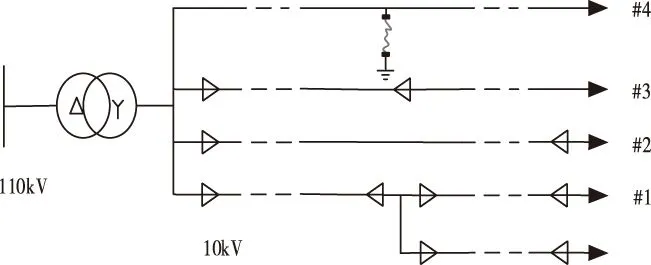
图7 10kV一次配网系统图

模型采用四条馈线全架空线路，全电缆线路，架空-电缆混合线路，电缆分支线路。馈线长度分别是7km、6.8km、6.8km和4km，其中馈线#1为电缆分支线路，#2为全电缆线路，电缆型号为YJV22-240/10kV；馈线#3为架空-电缆混合线路，馈线#4为全架空线路，型号为JKLYJ-120/10kV，故障点设在馈线#4末端，馈线参数设置如表2和3所示。

表2 架空线路参数

表3 电缆线路参数

根据上文的综合动态电弧模型，建立了10kV配电网中性点不接地的单相电弧接地故障仿真模型，仿真时长为0.2s，三相对地电容分别为：4.8μF、5μF、5.2μF。系统经历单相发生3次对地燃弧、3次工频电流过零熄弧过程。利用ATP中的TACS控制模块来控制Mayr模型瞬时电流与Cassie模型瞬时电压，非线性时变等效电阻由TYPE91/TYPE90可控型电阻模块来模拟，仿真模型如图8所示。

图8 间歇性电弧仿真模型

4 间歇性弧光接地故障仿真结果

由间歇性弧光接地模型得出三相电压波形变化曲线，系统三相电压波形失去正弦对称性，但仍具有周期性[20][21]。故障相A相经过两个周波后电压达到峰值，在20ms时接地，随后在电弧电流过零点25ms时熄灭，后在40ms时发生第二次重燃，再经过半个周波45ms时熄灭，第三次重燃在60ms开始，经过半个周波到结束时呈现稳态性电弧接地，如下图9所示。

图9 间歇性电弧三相电压电流波形图

系统每次发生电弧接地都会引起系统高频振荡，非故障B、C相的电压峰值达到相电压的2.6倍，B、C两相的过电压波形畸变具有相似性。故障A相在燃弧是电阻值较小，后半个周波电弧呈现高阻特性，在电流过零后熄灭，电压波形恢复正弦性。

根据“工频熄弧理论[16]”得出弧光接地过电压波形如图10所示。在整个燃弧和熄弧过程中，配电系统中累积的能量是产生间歇性弧光过电压的主要因素，系统每次发生电弧接地都会引起高频振荡，过电压会随着重燃次数的增加而增大。

图10 系统3次燃弧中性点电压波形

如图11所示，当故障相馈线为架空线路时，明显的非故障相电压畸变幅度更大，且其峰值电压要远高于故障相。相对比，馈线为电缆和架空线路混合时，故障相峰值电压畸变程度要比单一架空线路加深，非故障相的峰值电压远高于故障相，非故障相电压畸变更加严重。

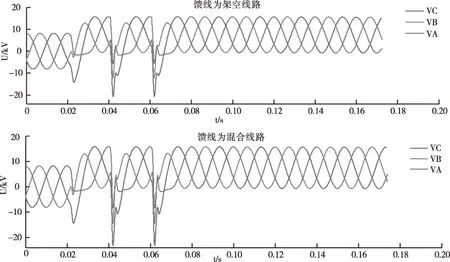
图11 不同馈线的间歇性电弧电压波形

5 间歇性弧光接地故障仿真结果分析

在设置配电网故障馈线时，考虑到现有的配电线路形式并非单一，故在架空线路、电缆分支和架空-电缆混合线路三种不同馈线类型下分别设置弧光接地故障，各馈线参数设置如表2、3所示，记录仿真时各类线路类型的电弧电流，结果如表4所示。

表4 馈线差异对应燃弧峰值电流

当间隙性弧光接地故障发生在不同类型的馈线上，其对应的重燃故障峰值电流各不相同。由表4可知，纯电缆线路要比架空线路的各类峰值电流高约2.54%，混合线路要比单一架空线路的馈线峰值电流高约3.76%。结果分析可知，接入电缆比例越大，故障电流对应越大，随着线路类型和结构的变化，其对应的故障严重程度不同。

各类单相接地故障研究中，线路长度、短路时刻和故障点设置等诸多因素均与间歇性弧光接地故障相关，故设置混合线路A相发生随机故障点5km和8.75km处，取某峰值时间发生接地故障，结果如表5所示。

表5 不同故障点的电弧重燃峰值电流

如表5所示，将故障点设置在不同位置处，线路5km处发生2次工频熄弧、3次重燃间歇性弧光接地故障时，随着电弧重燃次数增加故障电流峰值越大。当故障位置发生变化，在8.75km处发生的弧光接地故障，2次工频熄弧、3次燃弧峰值电流均比5km处高2.47%，整体故障程度要比5km的更严重。分析可知随着单相接地电弧发生位置不同，线路对地电容电流会直接影响故障点的电流峰值。

本文综合考虑弧长对于电弧模型的影响，上文已分析了单相接地故障中不同弧长对应的零休状态的差异，现将取弧长为50cm、80cm、100cm和120cm对应的弧光接地故障中电流进行对比分析，如图12所示。

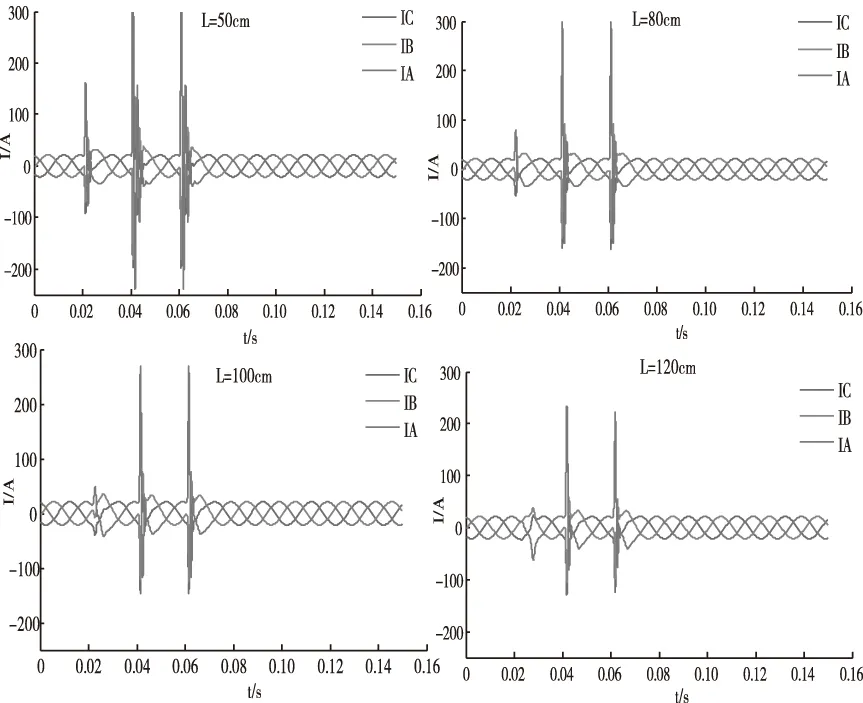
图12 不同弧长下的间歇性弧光电流波形输出

由图12所示的电流波形对比可知，弧长为50cm的首次接地故障峰值电流为150A，而弧长为120cm的首次接地故障峰值电流减小为80A，第一、二次重燃故障电流峰值会随着弧长增加而减小，故障相的电流变化最明显，可知不同弧长的电弧模型对间歇性接地故障均有影响。为对比清晰，如图13将四种不同弧长对应的首次接地故障峰值电流和一、二次重燃故障电流峰值进行对比，可知弧长为50cm时的电流值波动最明显，弧长为100cm时的电流值波动相对平缓。

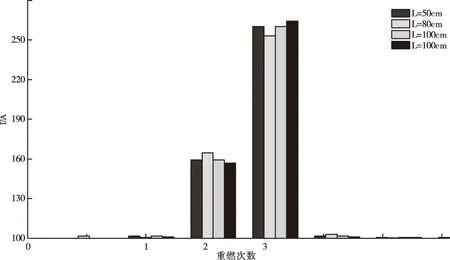
图13 不同弧长下的3次熄弧电流峰值对比

由于绝缘水平较低和薄弱老旧电气设备的存在，会使实际的谐波更加丰富。现将间歇性弧光接地故障时的电流进行FFT分解，如图14的电弧电流频谱分析可知，基波含量远高于其它次谐波，存在大量奇次谐波，且随着谐波次数增加，谐波量逐渐衰减，由于电流畸变并不显著，工频分量幅值较小，谐波次数也较多，故障时对通讯线路的电磁干扰相对其它中性点接地方式较小，但对系统动态稳定性的影响较大。

图14 故障电流谐波量分析

为将馈线出口处的相电压和相电流作为故障点的电压和电流[22]，故分析了故障相和非故障相的电压和电流，给出对应的伏安特性曲线，如图2所示的仿真，设置时长为0.04-0.3s，由所测数据绘出A、B、C三相电压-电流伏安特性曲线，故障相为A相。

如图15示，综合动态电弧模型故障点的伏安特性曲线近似与磁滞回曲线[17]，呈明显的非线性特征，电压电流在过零状态时，伏安特性曲线斜率较大，随电压和电流增大，曲线斜率逐渐恢复平稳，之后电压持续升高，曲线斜率基本保持不变。而非故障相的伏安特性曲线近似线性关系，没有明显的畸变。通过对故障相伏安特性曲线斜率的分析可知，其变化反应故障点动态电阻的变化，在电流零休时刻，电弧电阻呈现高阻状态，随着电流升高，电弧电阻逐渐衰减，呈现低阻状态。

图15 三相测量伏安特性曲线图

6 结论

根据上文中对电弧模型仿真及其应用场景的分析可以认为：

1)由于SLG故障中的电弧含有弧光过电压的特性，因此对SLG故障中的电弧应在传统模型的基础上增加变弧长等参量构成综合型动态非线性电阻模型。

2)对比传统电弧模型和改进型电弧模型，分析各动态变量对电弧特性的影响，后者的弧长变量可直观反应故障拉弧情况，仿真结果表明与实测接地故障特性基本吻合。

3)将此模型应用到实际的中压配电网中，分析可知弧长变化引起的电弧电阻暂态和稳定特性变化为：稳态电弧电导随着电弧长度的增大逐渐减小，对应的电弧电压增大，电弧电流出现更加显著的零休状态。根据瞬时电弧电流和电压得出接地非线性电阻的伏安特性，其曲线斜率直接反应故障点动态电阻变化，在电流零休时刻，电弧电阻呈现高阻状态，随着电流升高，电弧电阻逐渐衰减，呈现低阻状态。分别模拟电缆和架空线路以及混合线路对电弧特性的影响，可知馈线为电缆和架空线路混合时，故障相和非故障相峰值电压畸变更加严重。