基于社交学习理论的鲸鱼优化算法

郭振洲，郝亚茹，拱长青

(沈阳航空航天大学计算机学院，辽宁 沈阳 110136)

1 引言

2016年澳大利亚学者Mirjalili通过观察座头鲸捕食，提出了鲸鱼优化算法(WOA)[1]。该算法的主要思想是通过模仿座头鲸的捕食行为实现对目标问题求解。鲸鱼优化算法具有调节参数少，原理简单便于编程实现的优点，该算法自提出后受到研究学者广泛的关注，许多改进算法相继被提出。例如：Ling[2]提出了基于levy飞行的鲸鱼优化算法，将果蝇的运动轨迹和鲸鱼算法的运动轨迹结合通过改变开发阶段的运行路线从而增加算法的多样性。王坚浩等[3]使用Tent混沌映射生成混沌序列完成种群初始化，并使用混沌扰动协同更新策略改进收敛因子和惯性权重提出了基于混沌的鲸鱼优化算法(CWOA)。Dharmbir[4]将混沌鲸鱼优化算法应用于电力系统暂态稳定约束最优潮流(OPF)问题的求解。通过选择两个测试电力系统，验证了CWOA算法的有效性。郭振洲等[5]提出了基于自适应权重和柯西变异鲸鱼优化算法(WOAWC)动态调节算法权重并在算法勘探阶段引入柯西变异提高算法的收敛速度，Feng[6]提出了求解大规模问题的改进鲸鱼优化算法，在算法的初始阶段加入对立策略加快算法的收敛性，并引入非线性调节系数和变异操作提高算法的多样性和收敛性。以上对鲸鱼算法的改进集中在算法本身算子或初始化方法的改进，并没有从整体算法策略上加以修改。本文针对鲸鱼优化算法中个体信息交互少的特点，引入社交学习理论，强调个体之间的信息交互，通过在原算法的思想中加入社交学习理论从而提高算法的多样性和收敛性。

社交学习[7]是个体在社交网络中学习进步的一种有效途径。它是指同一群体间待学习个体向目标个体进行学习的一种社交方式。针对鲸鱼算法随机选择参考鲸鱼的勘探方法及逐次向上一代最优个体靠拢的策略，本文分别将社交学习理论应用到鲸鱼优化算法的勘探和开发阶段提出了社交学习鲸鱼优化算法(SLWOA)。在算法全局勘探和局部开发阶段引入社交学习理论，指导个体有意识的向潜在解进行勘探和开发。首先，随机挑选出一个个体作为参考鲸鱼，对比该个体的学习概率上限判断是否为待学习个体，然后根据判断结果选用不同的迭代公式进行更新，实现全局勘探。其次，通过对比剩余个体的学习概率上限确定待学习个体，并进行标记，然后对待学习个体进行社交学习，实现个体的局部寻优。

2 社交学习

2.1 社会学背景

1921年，英国科学家首次在Swaythling的小镇上观测到一些鸟类能够用喙打开牛奶瓶，随后的25年里，英国科学家观测到的这种鸟类的开瓶盖行为已经从大不列颠局部地区扩展到欧洲大陆，甚至扩展到全世界其它的鸟类。英国科学家认为这种行为产生的原因是群体中的个体不断向优于自己的个体进行学习，从而保持群体不断进化繁衍，这是社交学习生物学体现[8]。在过去的几十年中，社交学习理论中提出并讨论了各种机制，例如，刺激，增强和局部增强[9]，观察性调节[10]和社会促进[11]。而在这些机制中模仿机制一直被认为是最为重要的。基于这种理论，根据个体的适应度值将为个体设定学习概率上限，然后通过随机产生个体的学习概率值模拟个体的学习概率，对比个体的学习概率上限从而将群体中的个体分为待学习个体和非待学习个体，通过待学习个体向种群均值个体进行学习，保证个体不断进化且不会过早的陷入局部最优。2015年Jin[9]提出了基于社交学习的粒子群优化算法(SL-PSO)，并将社交学习算法概括为适应值评估、种群排序以及行为学习三个阶段。

2.2 种群排序和行为学习

个体作为群体中很小的一部分，所处位置不同，个体的优秀程度也不相同，通过种群个体排名的方法解决个体优秀程度判定的问题。假设个体排名越高越优秀，也就越容易作为学习的对象。若随机向比自己优秀的个体学习则会导致个体学习方向模糊，算法的收敛性降低，因而本文中使用该代种群算术平均值作为种群的学习对象，使用个体与该均值之间差值加权来表示个体向整体趋势学习的状况。

基于社交学习的待学习个体位置更新[10]如下方法：

(1)

(2)

其中以1-(i-1)/m表示学习概率和个体排名i成反比的关系，指数alog「n/m⎤则表示学习概率与维度n成反比的关系，从而模拟问题难度越大，个体越不会进行社交学习。对于每一代最优的个体因其无需向其它个体学习故其学习概率为0。学习因子ε调节整个社交学习行为，往往和问题的难度有关，作为调节学习步调的参数太大或太小都直接影响到算法的运行效果，本文设其运算表达式如下：

ε=0.1×n/100

(3)

其中m表示在群体中的个体数目，n表示群体中个体的维度。

3 鲸鱼优化算法

鲸鱼优化算法是模仿座头鲸捕食行为而提出的。自然界中座头鲸通过收缩包围，螺旋上升的策略实现猎食，算法中为了模拟座头鲸此种捕食策略，使用随机数作为辅助。首先随机产生一个小于1的数，若该数小于0.5则使用收缩包围模型，若该数数不小于0.5则使用螺旋上升模型。鲸鱼优化算法中具体的鲸鱼捕食过程主要包括三个部分:包围猎物、气泡攻击、搜寻猎物。

3.1 包围猎物

在此部分座头鲸并不知道食物的位置，算法中假设距离食物最近的鲸鱼就是当前的局部最优解，其它鲸鱼个体都会朝着这个位置靠近，从而完成包围猎物。具体位置更新如下方法

(4)

(5)

A=2ar-a

(6)

C=2r

(7)

其中A和C是系数向量，X*是局部最优解，且是α∈[0，2]从2线性递减到0，r∈[0，1]，c∈[0，2]。

3.2 气泡攻击

该部分为启发式算法中的开发阶段，该阶段的主要目的是在全局勘探找到潜在目标方向的基础上进行局部寻优。鲸鱼优化算法是通过收缩包围圈和螺旋更新位置的方式达到鲸鱼局部寻优的目的。

3.2.1 收缩包围原理

根据式(5)鲸鱼群进行收缩包围。当|A|<1时，鲸鱼个体会向当前位置最优的鲸鱼靠近。并且|A|越大鲸鱼游走的步伐越大，|A|越小鲸鱼游走的步伐越小，从而控制收敛速度。

3.2.2 螺旋更新位置

首先计算与当前最优鲸鱼的距离，然后再以螺旋方式游走，螺旋游走方式更新如下方法

(8)

(9)

其中式(9)是鲸鱼个体到目前最好的鲸鱼距离向量，b是常量系数，l∈[-1，1]的随机数。pro∈[0，1]的随机数用来选择收缩包围或螺旋更新模型。该阶段更新如下方法

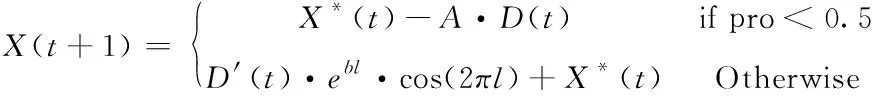
(10)

3.3 搜寻猎物

当|A|>1时，进入全局勘探阶段，该阶段主要目的是扩大搜索域，提高算法多样性，避免陷入局部最优。算法中通过随机选择策略，随机选择一个鲸鱼个体作为参考鲸鱼，然后其它鲸鱼均向其方向前进，从而实现猎物搜索如下方法

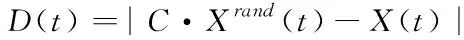
(11)

(12)

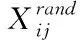
4 社交学习鲸鱼优化算法

4.1 算法思想

为了提高鲸鱼优化算法的全局寻优能力及收敛精度，引入社交学习策略即单独为待学习的后进生进行补习的方式，在算法的全局勘探和局部开发阶段对待学习的个体进行学习操作，提高群体收敛速度及收敛的精度。鲸鱼优化算法的全局勘探阶段，由式(11)和(12)可知，需要在该代种群中随机选择一头鲸鱼作为参考鲸鱼，然后其它鲸鱼依次向其靠拢，从而不断更新鲸鱼位置。参考鲸鱼的选择直接影响到算法收敛速度，本文在全局勘探阶段引入学习因子和学习概率，首先参考鲸鱼对比个体学习概率上限，从而判断是否需要学习，待学习个体则向群体的均值趋势进行偏移，从而完成参考鲸鱼的学习，该方式通过主动选择最有“潜力”的参考个体，避免不必要的采样，从而提高算法的收敛速度。勘探阶段改进如下方法

X(t+1)

Δ(t)=Ave(t)-X(t)

(15)

(16)

式(15)表示均值个体与当前个体之间的矢量距离，式(16)为理想均值个体的计算公式。在鲸鱼优化算法中局部开发阶段，位置更新迭代的式(10)无论收缩包围还是螺旋上升均是基于当前的局部最优解X*，缺少与外界信息交互，使得算法很容易陷入局部最优，故而引入社交学习的理论针对待学习个体向群体均值个体进行学习，从而提高个体之间的信息交互能力。此外将群体个体依照学习概率上限分为两个部分，对待学习个体单独进行学习操作，能够有效的减少算法的计算次数及群体中个体之间的差距从而提高算法收敛精度。在算法的开发阶段具体的操作流程为首先通过学习概率来区分是否为待学习个体，然后在待学习个体中引入种群均值个体作为学习对象，而其它个体则保持原有的更新策略。开发阶段改进如下方法：

4.2 算法流程图

社交学习鲸鱼优化算法分别在勘探和开发阶段对算法进行改进，具体的算法流程如图1。

图1 社交学习鲸鱼优化算法流程图

5 实验与结果分析

5.1 实验设计

为验证SLWOA算法的性能，分别在22个基准函数[11]进行30次测试，其中包括7组单峰函数、6组可变维多峰测试函数和9组固定维测试函数，见表1～3。另外本文分别对Sphere，RosenBrock以及Griewank函数进行若干平移，平移量见表4。

表1 单峰测试函数

表2 可变维多峰测试函数

表3 固定维多峰测试函数

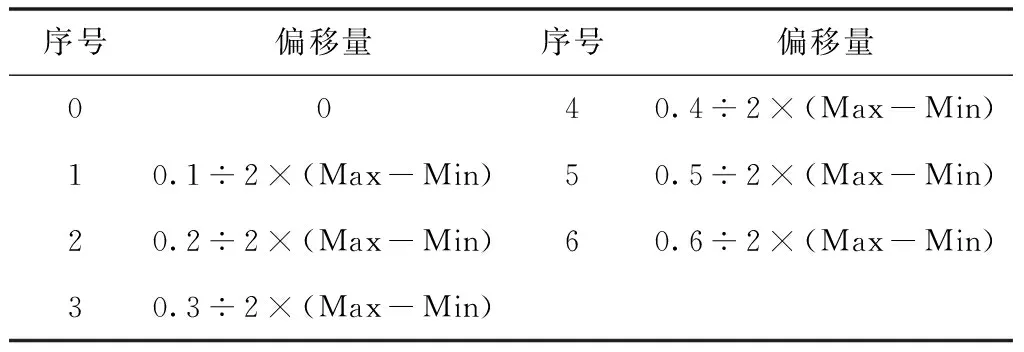
表4 基准函数的位置偏移

本文所有实验均在CPU 主频3.90GHz的Intel Core(TM) i3-7l00h、内存8GB的PC机上进行，操作系统为Microsoft Windows 10专业版，编程工具MATLAB R2015b。

5.2 实验结果及分析

本实验中SLWOA算法及其对比的四种算法的种群规模均为30，最大迭代次数均为1000，参数设置见表5。

表5 优化算法的参数

5种算法在22个测试函数独立运行30次寻优计算的均值和标准差见表6。其中最优者用黑体标注。表中“+”表示SLWOA算法效果优于该列算法;“=”表示SLWOA算法效果与该列算法的效果相当;“-”表示SLWOA算法效果不如该列算法。部分测试函数的收敛曲线如图2。对Sphere，RosenBrock以及Griewank函数的7次位置偏移，运行30次的平均值见表7。

表6 5种算法在22个基准函数上的测试结果

图2 部分测试函数收敛曲线

表7 平移函数运行30次均值结果

根据表6结果可知SLWOA在f1-f13相比其它四种算法结果均为最优，结合图2中算法的收敛曲线SLWOA在单峰函数f3上能够较快地得到全局最优解且在收敛速度和搜索精度上优于其它四种算法。这是因为在单峰函数中不存在多个最优解，而SLWOA算法通过引入均值，确保个体向种群行动总趋势的方向移动，提高了算法的收敛速度。尽管WOA算法、WOAWC算法在测试函数f9和f11上也获得了全局最优解，但结合图2中f9可以看出SLWOA算法在收敛速度方面均优于WOA和WOAWC算法。这说明在多模态空间中，SLWOA算法经过若干次的迭代运算之后仍具有跳出局部最优解的能力。待学习的个体进行学习操作，能够有针对性的提高个体的优秀程度;提高种群每次迭代后结果的准确度。在f14-f22函数中，SLWOA算法在标准差最小的情况下结果仍优于其它四种算法说明SLWOA算法在函数f14、f21，f22中不仅能够获得好的结果，而且还稳定收敛于这个解，因为是针对待学习的个体进行学习过程，是一种类似于后进生补习的方式，弥补了群体之间的差距缩小了群体成绩的标准差从而提高了结果的稳定性。表7可知，随着函数纵轴位置偏移的变大，SLWOA在偏移函数Sphere，RoseBrock，Griewank，的结果始终最优，即SLWOA算法在该类偏移函数上具有稳定性。除此之外对于多峰函数Girewank均选择最值的标准差和其平均值在同一个数量级上的结果，以此排除了某一次陷入局部最优。综上可知通过加入社交学习，针对性的为待学习个体补习，弥补群体间的优劣差距，从而达到提高收敛速度和稳定性的功能。

6 结论

本文将社交学习的理论应用于鲸鱼优化算法之中，在鲸鱼算法的勘探和开发阶段对适应值较差的个体根据学习概率判断是否需要进行社交学习，然后通过学习因子对学习程度进行控制。SLWOA算法相比于传统的鲸鱼算法提高了算法的收敛精度，从而避免鲸鱼算法陷入局部最优解的问题，同时也进一步提高了鲸鱼个体的全局搜索能力和局部寻优能力。通过对比5种算法在22个基准函数独立运行30次的均值和标准差并结合函数的收敛曲线，实验结果显示除了f15-f20函数组，SLWOA算法在收敛速度和收敛精度方面都有要优于其它四种对比算法。为了排除原点收敛的影响，对Sphere，RoseBrock，Griewank函数分别根据函数边界进行7次偏移并独立运行30次求均值，而SLWOA的结果在这21个偏移函数中结果均为最优。故此可认为引入社交学习提高了算法的稳定性和收敛速度，除此之外也说明社交学习鲸鱼优化算法适用于单峰函数和可变维多峰函数的应用场景，而对于固定维测试函数的应用场景的优势不明显。