循环流化床锅炉燃烧系统的建模与研究

晏 恒，胡林静，仝傲宇

(内蒙古工业大学电力学院，内蒙古 呼和浩特 010080)

1 引言

循环流化床锅炉 (Circulating Fluidized Bed Boiler，CFBB)是近几十年以来迅速发展起来的一种新型燃烧适应性广、稳定高效、环保性能优越的清洁燃料燃烧技术，并在全世界越来越受到广泛重视。其燃烧系统的被控对象具有多变量、非线性、强耦合、大惯性等特点，是一类典型的难控的热工对象。

国内的300MW CFBB的研发处在发展上升阶段，较多学者对当前循环流化床燃烧系统采用以给煤量和一次风量的配比的变化来反映床温和主汽压，在控制运行中主要的调节和控制手段都是为了实现主蒸汽压力和床温的稳定，但未能兼顾燃烧过程的经济性和稳定性[1-3]。且所建立的模型动态性复杂，在实现锅炉自动控制中仍存在一些问题[4-5]。为了实现有效的控制，解决复杂模型带来的掣肘，文献[6]通过定义输入量的动态阶，利用最小二乘支持向量机算法实时预测床温，并利用遗传算法对机组进行离线寻优从而建立床温模型。文献[7]将PLS和OLS算法和径向基函数神经网络结合，通过网络训练和数据泛化，然后用算法优化，得出较高精度的燃烧过程模型。文献[8]理论分析了锅炉大型化中二次风穿透问题和燃烧系统强耦合问题，并利用编制的辨识软件，建立了燃烧系统和床压系统的线性模型。尽管这些文章以不同方式从不同方面对循环流化床锅炉进行了建模，但是繁杂的附加条件在工业过程中通常难以满足，无法被广泛接受，同时算法的参数整定较为繁杂、理论上分析较多，泛化性不强。

考虑到以上问题，结合蒙西发电厂机组运行的历史数据，针对无外置式热交换器的循环流化床锅炉建立以给煤量、一次风量和排渣量为输入量，床温和主蒸汽压力为目标控制量的燃烧系统模型。并在机组50%、70%与100%三种典型工况下，通过辨识、拟合仿真、验证，分析燃烧系统的动态特性，保证了所建模型的精度性和可靠性。

2 系统模型辨识理论及方法研究

2.1 建模辨识原理

灰箱建模是将机理建模和辨识建模相结合的建模方式。一方面可以利用专家对过程控制领域已有的经验去了解和分析系统本身的结构特性和运动规律；另一方面通过系统历史运行的输入输出数据，估计出可以表征该系统的输入输出之间关系的数学关系式，关系式中的结构和参数必然可以反映出系统的动态特性[9]。本文针对循环流化床锅炉燃烧系统的特性，研究主要因素忽略次要因素，将燃烧系统简化成图1所示系统。

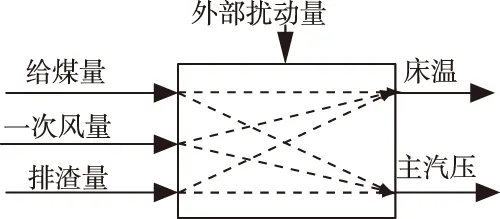
图1 循环流化床燃烧系统简图

循环流化床燃烧系统是一个典型的多输入多输出(MI/MO )的非线性系统。可以将这样一个MI/MO系统看作多个单输入单输出(SI/SO)的系统叠加的形式。对于每SI/SO

系统，通过采集能够代表系统动态特性的输入输出数据，运用建模理论，以目标函数值(即，采样数据输出值和模型输出值的差)

作为辨识算法的准则函数，当拟合的数据曲线均方差最小时，得出各工况点下的线性传递函数模型集，从而确定出实际系统的近似模型。

其中模型集的描述是建模的关键，根据现场数据的输出响应曲线的特性，结合专家总结的经验，表征循环流化床锅炉燃烧系统在不同工况点附近的动态特征可用如下经验模型集

(1)

其中对于延迟时间τ的辨识，是将其放在参数辨识的过程中，增加参数的辨识个数，运用粒子群算法同时学习系统模型的结构和参数，将辨识过程看作曲线的拟合过程。辨识原理图如图2所示。

图2 系统辨识过程原理图

由图2可知，在给定输入下，若确定了式(1)中K，T，a，n，τ各参数在一定的误差范围内时，模型输出y′(t)与实际系统输出y(t)匹配度较高，则表示当前模型参数求取符合要求。

2.2 数据处理

为了尽可能地消除采集数据的漂移和无用低频段信息对建模的影响，以下三个原则有利于在电厂运行的大量数据中选择合理辨识模型的数据：①采样周期应满足香农采样定理。②七点三次平滑滤波法是基于多项式最小二乘曲线拟合原理的运动平滑滤波方法。其原理是通过处理采样数据中的每七个点并将其转换为三个点的多项式的值的方式对原始数据进行过滤和去噪。③为了剔除采集数据中远远超过实际范围的奇异数据。通过采用“3σ准则”检验法可以达到预期效果。

以50%工况下对给煤量进行数据处理为例，处理前后效果如图3所示。

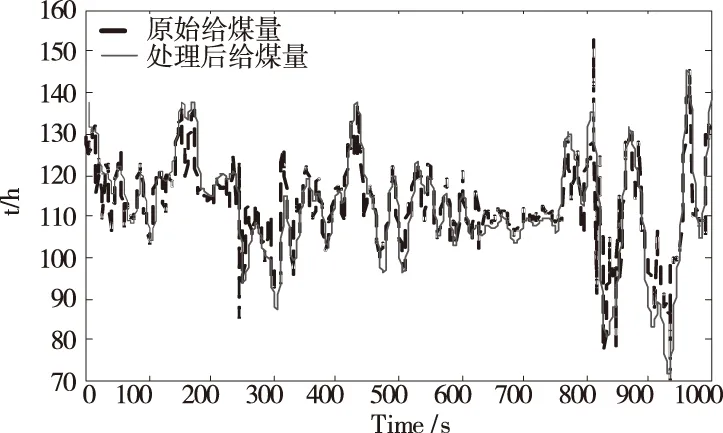
图3 50%工况下给煤量处理效果图

2.3 基于改进粒子群算法的参数辨识

由图2看出，模型辨识本质上就是通过输入输出数据确定模型集的一种演算，在分析对象的输出响应下，估计出对象的模型类型，即式(1)的K，T，a，n，τ的恰当组合。本文采用的粒子群算法在收敛情况下，可以避免模型结构参数对系统的影响，快速地辨识出相应的模型。

粒子群算法(PSO)描述如下：在PSO中，q个粒子群组成q组可能解，其中，第i个粒子的位置表示为向量

Yi=(yi1，yi2，…，yiN)，i=1，2，…，q

(2)

其速度标记为：Vi=(vi1，vi2，…，viN)。随机产生一组Yi(初代种群)，Yi带入优化问题O(Y)中就可以计算其适应值，根据适应值的大小衡量Yi的优劣程度[10]。

本文以目标函数作为准则函数，通过求最小值，使目标函数值越小，则对应的适应值越好。设粒子i到目前为止搜索最好的位置记为：Y-est。则粒子i的此时最好位置为

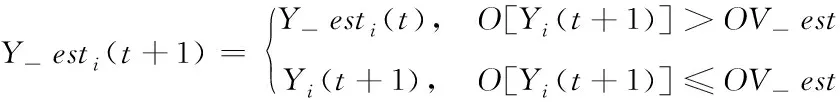
(3)

寻优过程中粒子群经历的最优位置记为Y-estg，通过式(4)更新当前速度，通过下面式(5)更新当前的位置。

vin(t+1)=vin+C1×rand()×(Y-estin-yin(t))

+C2×rand()×(Y-estgn-yin(t))

(4)

yin(t+1)=yin(t)+vin(t+1)

(5)

改进粒子群算法是指带惯性权重的PSO，引入惯性权重w以协调全局搜索和局部搜索的程度。即，

vin(t+1)=wvin+C1×rand()×(Y-estin-yin(t))

+C2×rand()×(Y-estgn-yin(t))

(6)

其中，w采用线性递减策略，其值的范围通常为[0，2]。C1与C2为认知因子，在算法收敛范围内，w越大，粒子全局搜索能力较强；w越小，局部搜索能力较强。参数的选取是影响算法性能和效率的关键，当C1、C2、w在一定范围内取值时PSO算法具有收敛解[11-12]。

3 床温和主汽压力的辨识

3.1 床温的辨识

由热工特性和过程控制经验可知，给煤量引起床温的变化过程具有纯延迟、大惯性和自平衡特性。在本文中选取的模型集可以代表其模型的所有特征。

模型的辨识思想分两步：

1)筛选出能够代表燃烧系统动态特性的运行数据后，经过数据处理，利用粒子群算法辨识出床温在50%、70%和100%三工况点附近的估计模型，选择粒子群算法的准则函数最小时的仿真结果，得出的模型基本上能反映输入输出数据的数学关系。但是，此类模型并不能证明被控量是由某一种输入量的变化单一引起的，其模型下的热工特性不一定准确，必须经过在该工况点下的其它无关数据去验证[13]。

2)为了验证模型的有效性，本文通过赋予输入量一个扰动信号，其床温必然也会跟着发生变化，将初始时刻的床温标记为0基准，则床温的变化量ΔT便可以得出。 记录每个床温的变化值ΔT，将与真实数据相比较，拟合程度最匹配时，确定模型参数[14]。

以给煤量-床温的辨识为例：

1)给煤量为给煤机煤量反馈值之和，床温为6个床温信号采集点的均值。在3种工况下，先对原始给煤量数据进行预处理，通过遍历阶次n的值(通常取1～5，综合实际考虑和每次辨识的误差结果，当n=2时，拟合效果符合预期)，采用粒子群算法辨识出模型各参数。(1)式中的参数变化范围是：比例系数K∈(0，7)，惯性环节的时间常数T ∈(0，500)，微分环节常数a ∈(0，1)，延迟时间τ∈(0，500)。在PSO中粒子个数为80、优化代数为100、w=[0.8 1.2]、C1、C2=[1.8 2]、采样时间为10s。仿真得出的模型拟合效果图如图4所示。此时3工况下的拟合误差分别为0.0083、0.0052、0.0024。

图4 给煤量的变化对床温的辨识结果

由误差范围内的辨识拟合结果，得出3工况下给煤量-床温的传递函数近似模型。

50%工况：

(7)

70%工况：

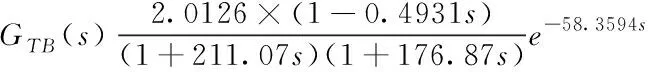
(8)

100%工况：

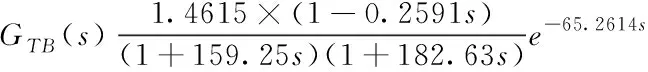
(9)

2)在上述的理论研究和已知3种工况下给煤量-床温模型的基础上，通过对给煤量模型施加阶跃信号后，每隔100s记录相对应床温的变化值ΔT，最后和同机组同工况下的实际床温数据做拟合效果对比，就可保证了在该数据段内，影响床温的其它因素尽可能是不参与到辨识过程中，床温的波动是由给煤量单独引起的，从而增加了模型的准确性，验证了辨识模型的可信度。

以50%工况下的给煤量-床温的模型为例，记录测试时间段内床温变化值列表如表1所示。对模型的验证结果如图5所示。

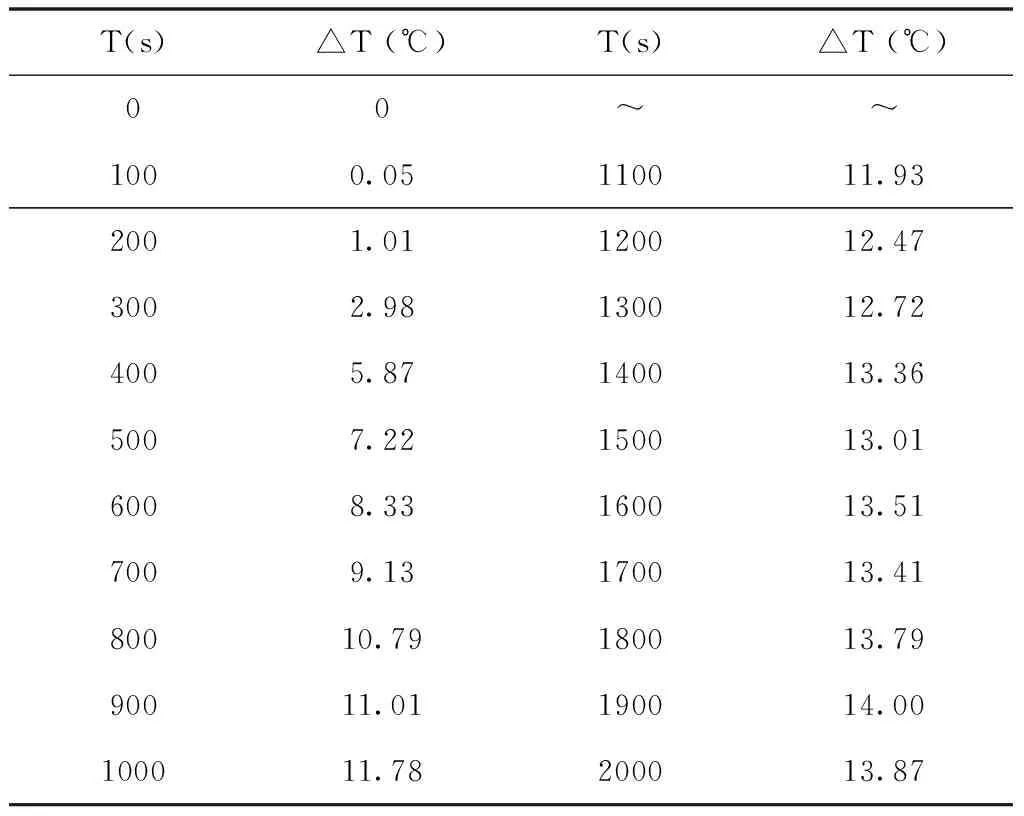
表1 给煤量扰动下的床温变化值

图5 给煤量阶跃扰动下的床温变化

由图4中的拟合曲线和图5中的验证性曲线可知，燃料煤粉经过给煤机传送进炉膛内燃烧的过程是一个缓慢的过程，具有延时性，可以首先，低温的煤粉由于进入炉膛后会先吸收部分热量破裂燃烧会致使床温呈现负温度，随着煤量的增加，燃烧的进行，煤粉放热使炉膛内温度惯性上升，最终趋于稳定[15]。

同理，对一次风量-床温和排渣量-床温的模型辨识做同样的处理，得出在同机组不同工况下的拟合曲线和模型参数：

在辨识时，图6的参数变化范围是：K∈(0，2)，T∈(0，800)，a∈(0，500)，n=2，τ∈(0，200)。PSO中粒子个数为80、优化代数为60、w=[0.9 1.7]、C1=C2=0.8、采样时间为10s。此时3工况下的拟合误差分别为0.0097、0.0122、0.0027。

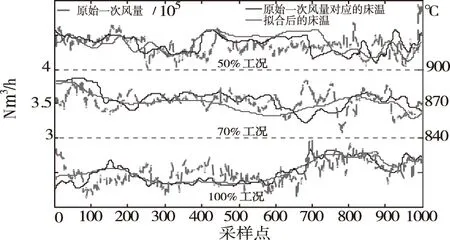
图6 一次风的变化对床温的辨识结果

图7 一次风量阶跃扰动下床温变化

结合PSO辨识结果，通过拟合图可知，一次风量加大使烟气从密相区带走的热量也在不断增多，致使床温下降。同时，风量越大，使炉膛内的颗粒流化作用更加剧[16]，

提供燃烧使用的氧量上升，从而燃烧放热量增加，造成床温上升。从整个过程来看床温体现出一定的惯性和延迟。

图8在PSO算法辨识过程中，(1)式中的各模型的参数变化范围是：K∈(0，10)，T∈(0，15)，a∈(0，4000)，n=2，τ∈(0，60)。PSO中粒子个数为60、优化代数为100、w=[0.2 1.2]、C1=C2=2、采样时间为10s。此时3工况下的拟合误差分别为0.0147、0.0053、0.0025。

图8 排渣量的变化对床温的辨识结果

图9 排渣量阶跃扰动下床温变化

由拟合图看出，随着排渣量的增加，炉膛废料从密相区带走的热量增加，使床温降低；同时随着外部冷空气的进入，床温进一步降低，其中存在一定的惯性和延迟[17]。随着排渣的进行到停止，炉膛密相区的氧气增加，煤粉粒的流化空间加大，炉内的燃烧反映加强，床温会逐渐上升。

同机组相应工况下，一次风量-床温和排渣量-床温的传递函数模型如下

50%工况

(10)

70%工况

(11)

100%工况

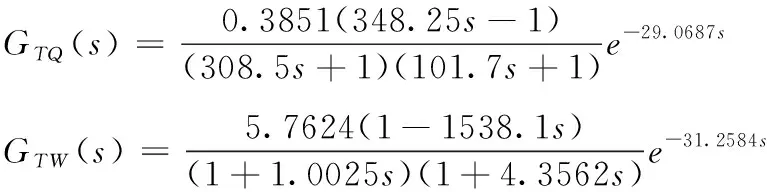
(12)

3.2 主蒸汽压力的辨识

同辨识床温，分两个步骤分别确定出给煤量-主汽压、一次风量-主汽压和排渣量-主汽压在同机组变工况下的系统模型，综合给煤量和一次风量变化引起主汽压力变化的热工特性，便于模型曲线的仿真观察，此处不再附加采集的原始给煤量和一次风量的数据曲线。

以给煤量-主汽压模型辨识为例：

1)同机组下，给煤量数据为给煤机煤量反馈值之和，主汽压力数据为各主汽调整阀门的总值。3种不同工况下，对原始给煤量数据处理后，采用粒子群算法辨识出的模型各参数。(1)式中的参数变化范围是：K∈(0，20)，T∈(0，100)，a∈(0，1)，n=2，τ∈(0，300)。在PSO中粒子个数为60、优化代数为100、w=[1.6 1.2]、C1、C2=[2.1 1.8]、采样时间为10s。仿真得出的模型拟合效果图如图10所示。此时3工况下的拟合误差分别为0.0109、0.0077、0.0003，辨识结果基本符合要求。

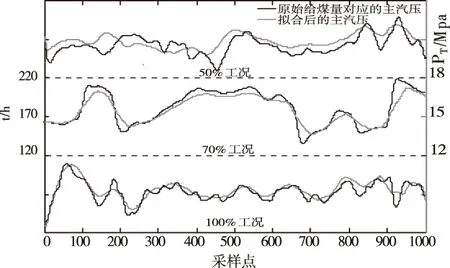
图10 给煤量的变化对主汽压的辨识结果

此时得出的3工况下给煤量-主汽压力的传递函数近似模型：

50%工况

(13)

70%工况

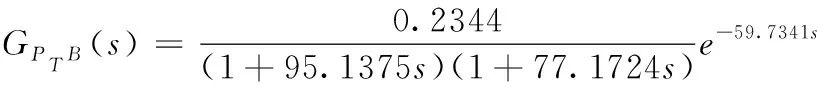
(14)

100%工况

(15)

2)结合3种工况点下给煤量-主汽压力的近似模型，通过对给煤量模型给与阶跃信号后，记录相对应主汽压力的变化值ΔP，最后和同机组同工况下的真实主汽压力数据做拟合效果对比。

以50%工况下给煤量-主汽压力模型为例，主汽压力变化值列表如下表2所示。对模型的验证结果如下图11所示。

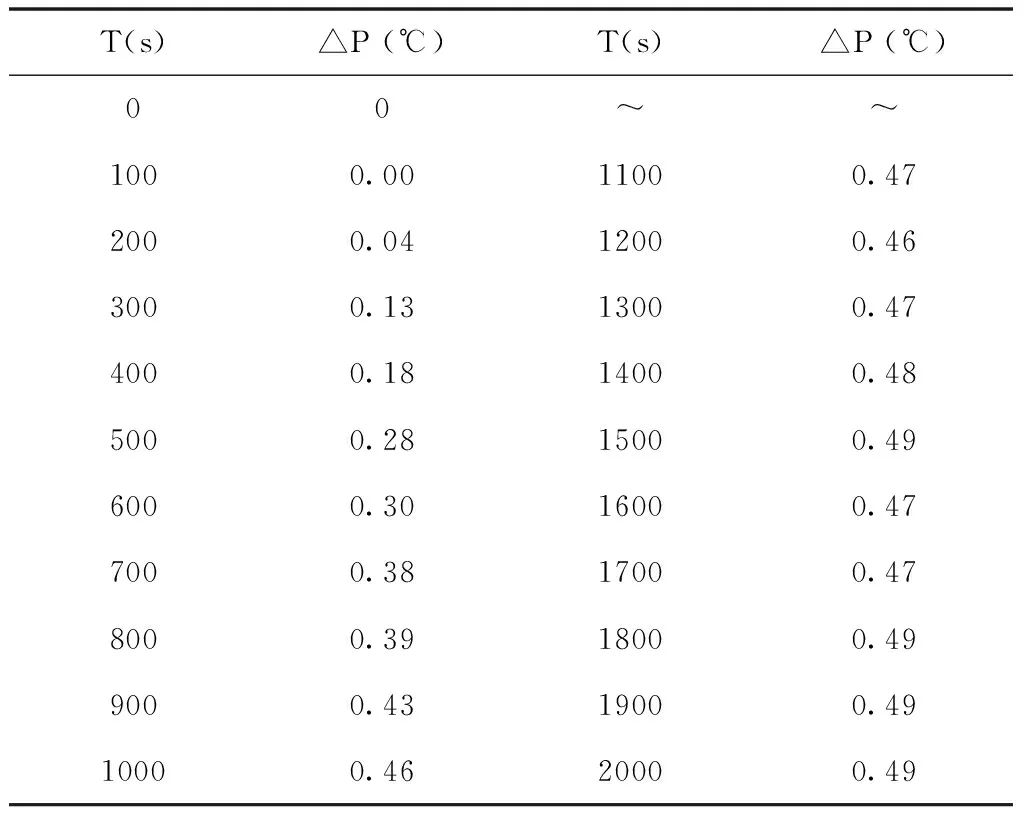
表2 给煤量扰动下的主汽压力变化值

图11 给煤量阶跃扰动下主汽压力的变化

由图10的拟合曲线和图11的验证性曲线可知，给煤量增加时，炉膛内热反应加剧，锅炉热负荷增强，蒸汽蒸发强度加剧，汽包内外的压力差增大使得蒸汽流量增加，主蒸汽压力增大[18]。主汽压力的滞后和惯性特性依旧明显，随着燃烧的进行，给煤给煤量变化较小时，主汽压力下降，最终趋于稳定。

同理，对一次风量-主汽压和排渣量-主汽压的辨识做同样的处理，得出同机组不同工况下的拟合曲线和和验证性仿真图。最终确定相应工况下的模型的传递函数。

图12在辨识处理过程中，同机组不同工况下，(1)式中的参数变化范围是：K∈(0，5)，T∈(0.01，300)，a∈(0，1)，n=2，τ∈(0，600)。PSO中粒子个数为80、优化代数为110、w=[0.8 1.2]、C1、C2=[2 2.2]、采样时间为10s。此时3工况下的拟合误差分别为0.0084、0.0102、0.0117。

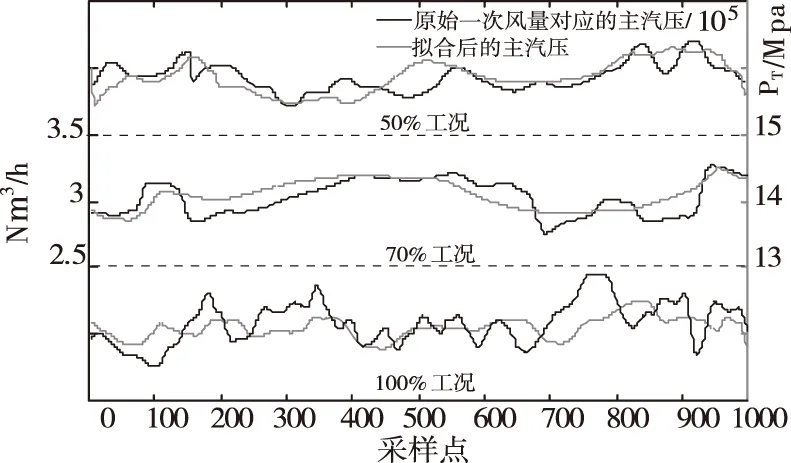
图12 一次风的变化对主汽压的辨识结果

结合PSO辨识的结果，由辨识拟合图和验证图表明，一次风量的增加会显著的加强炉膛内部的粗细颗粒的流化程度，使燃烧过程更加充分，从而剧烈的燃烧放热使水冷壁的热交换能力加剧，水的蒸发量增多，汽包内的压力增加，使主汽压升高[19]。反之，则具有相反的动态变化。此外，从时间域的动态响应可知，主汽压伴随一次风量的变化而变化时有时滞、大惯性等特点，符合研究对象的热工特征。

图13在辨识时，同机组不同工况下，(1)式中的参数变化范围是：K∈(0，5)，T∈(0.01，500)，a∈(0，1)，n=2，τ∈(0，300)。PSO中粒子个数为110、优化代数为100、w=[1 1]、C1、C2=2.1 、采样时间为10s。

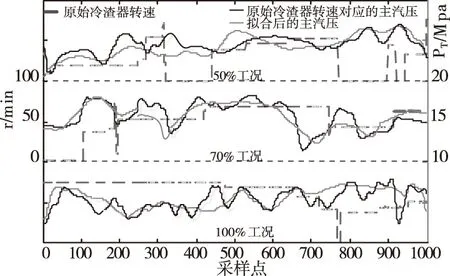
图13 排渣量的变化对主汽压的辨识结果

此时3工况下的拟合误差分别为0.0033、0.0021、0.0073。

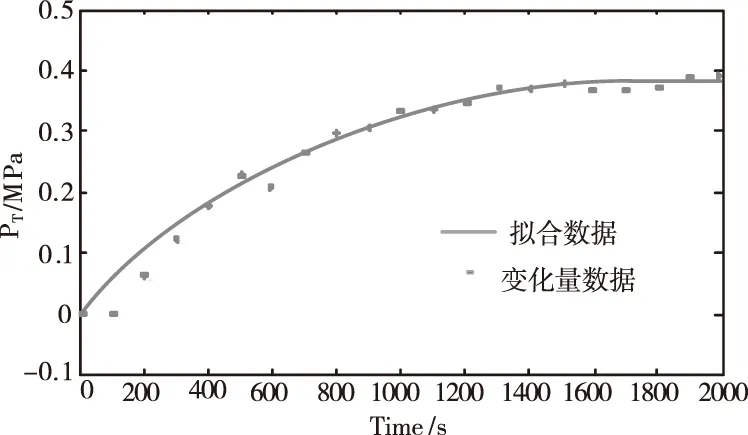
图14 排渣量阶跃扰动下主汽压力的变化

仿真表明，随着外部因素的稳定运行，排渣量的变化会造成炉内主汽压的波动。排渣量增大，由于水冷壁吸收的热量的变化过程有较大的延时性，使炉膛的温度呈现由强后转弱的变化，随之主汽压力先增大后减小。

相应工况下，一次风量-主汽压和排渣量-主汽压的传递函数模型如下：

50%工况

(16)

70%工况

(17)

100%工况

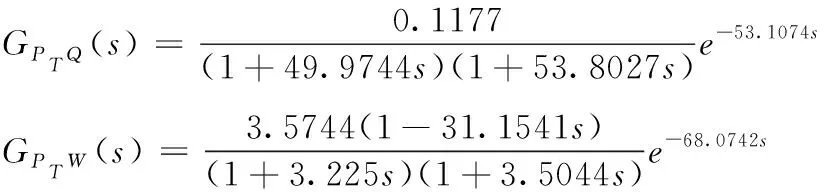
(18)

4 结果分析

基于上述仿真和策略分析，得出循环流

化床锅炉在50%、70%和100%工况下的燃烧系统模型传递函数矩阵。

(19)

其中，给煤量B的单位为t/h，一次风量Q的单位为Nm3/h，冷渣器转速W的单位为r/min，床温T的单位为℃，主汽压力PT的单位为MPa。

由文中模型拟合曲线和验证性仿真表明，本文所建立的GTB(s)、GTQ(s)、GTW(s)和GPTB(s)、GPTQ(s)、GPTW(s)各工况下模型的动态特性结果能够较好的匹配实际工程现场的运行数据，且拟合误差小、辨识的模型精度较高。

5 结论

由蒙西发电厂300MW循环流化床锅炉，通过筛选机组历史运行数据，用粒子群算法分别辨识出反映循环流化床锅炉燃烧系统在50%、70%、100%工况下的传递函数模型。分析了以给煤量、一次风量和排渣量对床温和主蒸汽压力变化的动态特性，建立了变工况下燃烧系统的多变量传递函数矩阵。拟合结果表明，在误差控制范围内，

所建立模型可完全表征对应工况下的系统特性，既体现出粒子群算法辨识模型参数的有效性，也为以后完善循环流化床锅炉系统设计提供参考。