下肢外骨骼机器人动态建模与步态跟踪LQR控制
刘 洋,彭世国,杜玉晓,廖维新
(1. 广东工业大学自动化学院,广东 广州510006;2. 香港中文大学机械与自动化系,香港999077)
1 引言
外骨骼机器人是基于仿生学和人体工程学设计的一种“套在人体外面”的可穿戴式机械装置。它将人类的智力和机器人的“体力”结合,靠人来控制机器人,通过机器人来完成仅靠人的自身能力无法单独完成的任务[1]。近几年来,因车祸和疾病导致下肢残疾或瘫痪的患者越来越多。为了帮助他们完成站立、坐下、行走等基本动作,辅助进行康复训练,研制一种高性能的下肢外骨骼机器人非常必要。为了使机器人的动作更灵活、更精准、更具有柔性,需要运用较精确的系统模型来实现步态轨迹高精度跟踪,这也成为该领域的研究热点之一。国内外学者提出的建模方法有:拉格朗日方程建模法[2-3],广义雅可比矩阵建模法[4]、五连杆模型[5]、七连杆模型[6]。基于不同的应用场景和不同的假设条件,这些方法所建立的模型有效。但是对于下肢外骨骼机器人的建模比较复杂,并且仅能建立机器人本体的数学模型。当使用者穿戴外骨骼服以后,以上建模方法不再适用人机一体化全系统的建模。关于机器人控制方案主要包括:PID控制[7]、重力补偿控制[8]、DMP轨迹规划控制[9]和模糊自适应控制[10]等。虽然不同方案在单个性能方面各有优点,但是诸多方案只是在理论和仿真方面开展研究。关于外骨骼机器人系统的设计与实现较少。
针对上述问题,提出一种将牛顿-欧拉公式与系统参数辨识相结合的方法,建立人机一体化外骨骼机器人全系统的动态模型,并进行下肢外骨骼机器人步态跟踪LQR控制设计。
2 下肢外骨骼机器人
通过与香港中文大学合作,项目组研制出一种可穿戴式下肢外骨骼服样机,命名为“CUHK-EXO”,如图1所示[11]。它主要以铝合金为骨骼材料,由安装在髋部和膝部的四个瑞士Maxon公司成套减速电机(包括编码器、直流伺服驱动电机和行星减速齿轮)驱动,给使用者的下肢运动提供外力。外骨骼服的尺寸可调节,适合不同身高的使用者。为了简便,采用被动式脚踝,不对踝关节的运动进行控制,足部看作小腿的一部分。

图1 CUHK-EXO机械结构及实物图
下肢外骨骼机器人CUHK-EXO的控制系统如图2所示。研华工控机作为主控制器,构成上位机系统,完成传感器信号处理、运动意图识别、步态轨迹分析和运动规划等功能。Arduino单片机作为从控制器,构成下位机系统,控制信号经驱动器放大后驱动4个不同的电机。关节角度、速度、力等信号经多路传感器检测后传输给主控制器进行处理。
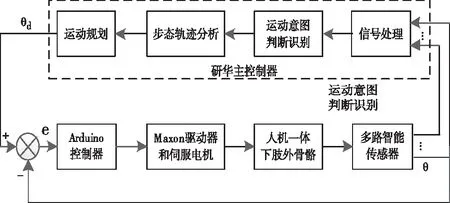
图2 下肢外骨骼机器人控制系统示意图
3 动力学建模
3.1 牛顿-欧拉方程
通常,刚体运动可以分解为质心的平动和绕质心的转动。质心的平动可以用牛顿方程描述,绕质心的转动可以用欧拉方程定义。因此,牛顿-欧拉方程表示为

(1)
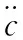
若刚体由i个构件组成,在基础坐标系中,如果fi-1,i表示构件i-1对构件i的作用力,fi,i+1表示构件i对构件i+1的作用力,fi表示构件i质心所受的外力,则作用在构件i上质心的合力可表示为
Fi=fi-1,i-fi,i+1+fi
(2)
如果li表示fi-1,i的力臂,hi表示fi,i+1的力臂,mi-1,i表示构件i-1对构件i的力矩,mi,i+1表示构件i对构件i+1的力矩,mi表示构件i质心所受的外力矩,则作用在构件i上质心的合力矩可表示为
Mi=mi-1,i+fi-1,i×li-mi,i+1-fi,i+1×hi+mi
(3)
3.2 牛顿欧拉法建模
当使用者穿戴下肢外骨骼服在行走过程中,下肢的摆动可以近似简化为二连杆结构的运动,如图2所示。以髋部为坐标原点O,大腿长度为L1,质量为m1,质心位置C1,距离原点l1,与竖直方向的夹角为θ1。以膝关节A为坐标原点,小腿长度为L2,质量为m2,质心位置C2,距离A点l2,与大腿延长线方向的夹角为θ2。
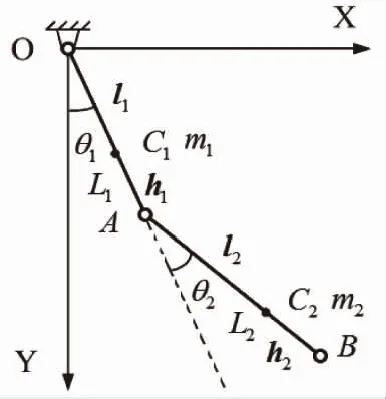
图3 下肢外骨骼机器人二连杆简化结构
根据式(1)(2)(3),对于大腿可列方程组
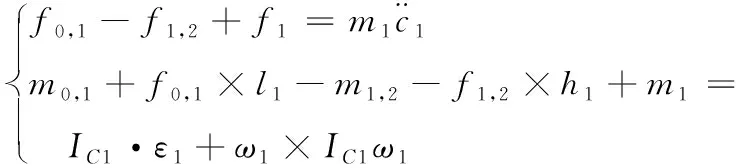
(4)
对于小腿可列方程组

(5)
对于二连杆结构
f0,1=f2,3=0
(6)
因为二连杆刚体在质心处仅受重力,所以
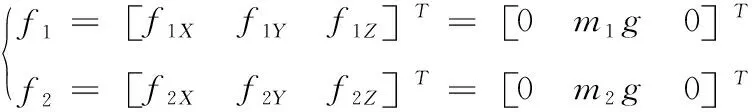
(7)
在质心处无其它外力矩,因此
m1=m2=0
(8)
假设外骨骼机器人在行走过程中,下肢运动始终保持在同一个平面,则有
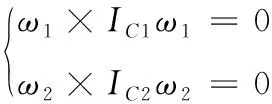
(9)
假设安装在髋关节的电机提供驱动力矩为T1,安装在膝关节电机提供的转矩为T2,则有
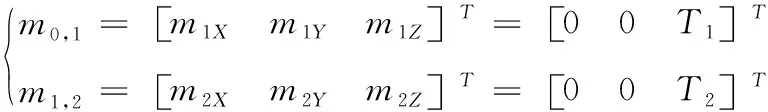
(10)
联立方程(4)-(10)得
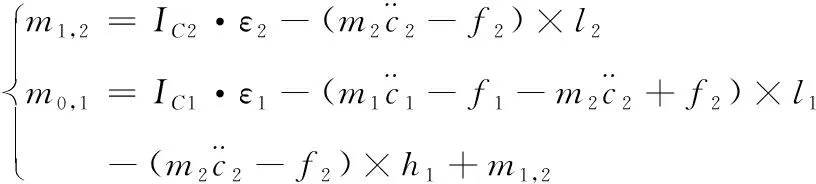
(11)
其中,大腿质心位置在XYZ方向上的分量表示为
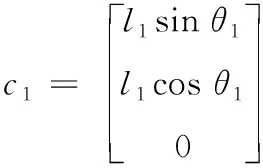
(12)
小腿质心位置在XYZ方向上的分量
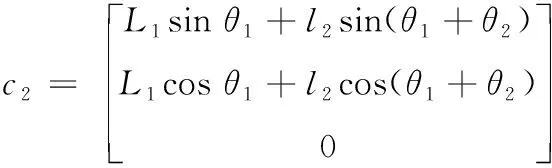
(13)
大腿的转动惯量在XYZ方向上的分量

(14)
小腿的转动惯量在XYZ方向上的分量

(15)
大腿质心距离原点的距离的三个分量
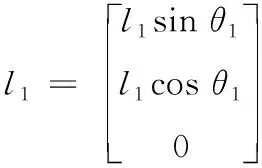
(16)
小腿质心距离原点的距离的三个分量

(17)
大腿对小腿作用力臂的三个分量
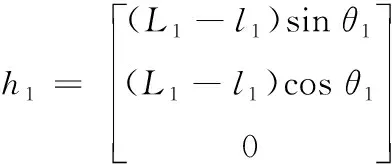
(18)
将(12)-(18)带入式(11),得数学模型
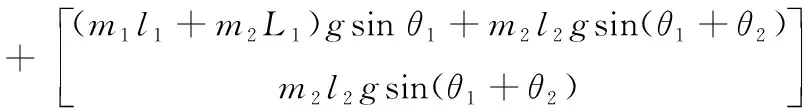
(19)
根据文献[12],髋关节运动方程为
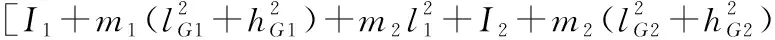
+2l1(m2lG2cosθ2-m2hG2sinθ2) ]1
+g[m1lG1sinθ1+m1hG1cosθ1+m2lG1sinθ1
+m2lG2sin(θ1+θ2)+m2hG2cos(θ1+θ2) ]
(20)
膝关节运动方程为


(21)
根据本项目实际,对式(20)(21)进行参数赋值

(22)
将式(22)代入式(20)(21),推导的结果与式(19)完全相同,验证了牛顿欧拉法建模正确。
3.3 系统参数辨识
一般地,一个典型n关节机器人,其动态特性可由二阶非线性微分方程描述[12]
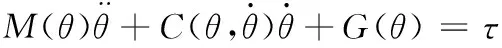
(23)
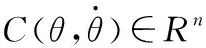
因此,式(19)可以写成如下形式
(24)
其中
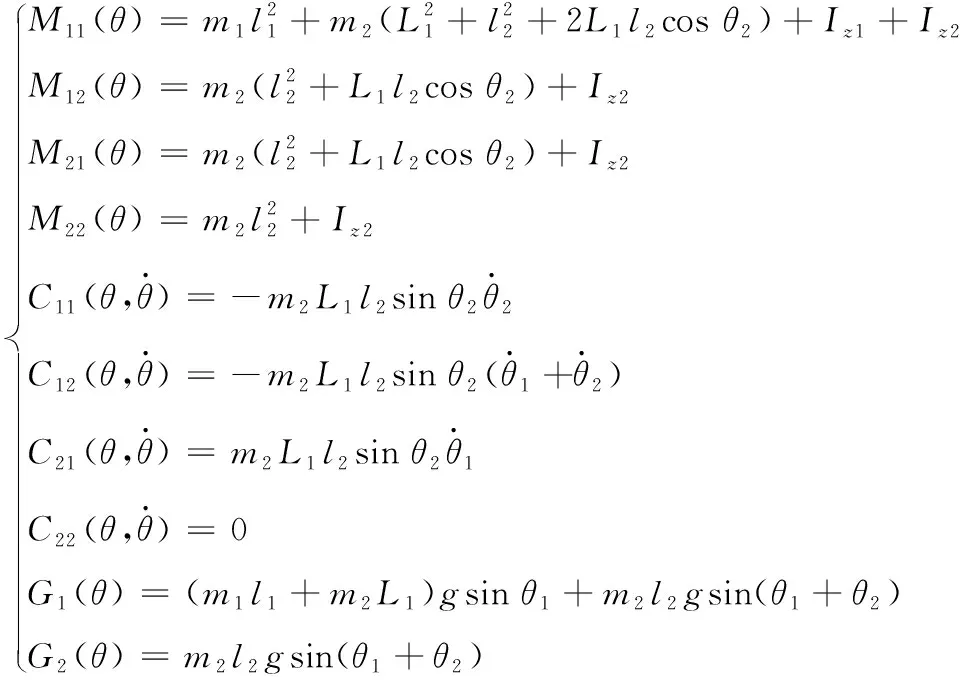
(25)
系统的质量惯性和转动惯量参数
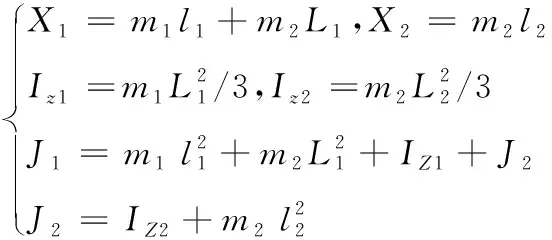
(26)
本项目中,外骨骼服的质量m0=20kg,实验者的质量mload=60kg,根据成年人生理的特点,大腿的质量
m1load≈0.1mload=6kg
(27)
小腿与足部的总质量
m2load≈0.061mload=3.66kg
(28)
由于人体肌肉组织分布比较均匀,为了计算简便,将大腿和小腿(包含脚)的质心都取在几何中心位置,则有
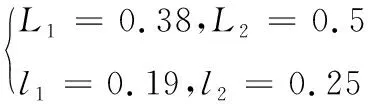
(29)
将式(31)(32)(33)代入(30)计算得到

(30)
由于外骨骼服的电机安装在髋关节和膝关节位置,大腿和小腿实际质心不在它们的几何中心位置,不能直接计算其转动惯量。文献[12]进行动力学参数辨识实验。先将其悬空吊起,再给驱动器发脉冲使电机运转,最后对角度和转矩的波形进行曲线拟合和数据分析,得到
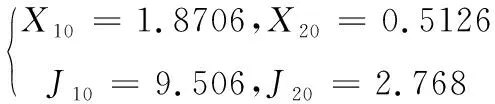
(31)
因此,综合考虑人机一体的外骨骼系统,参数如下
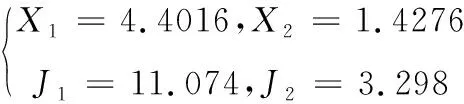
(32)
因此,式(25)中实际系统的动态模型参数如下
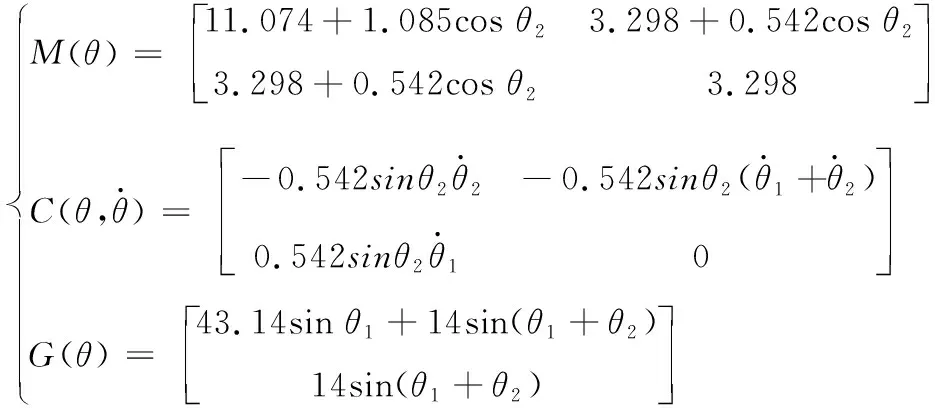
(33)
4 步态轨迹的LQR控制
4.1 LQR基本原理
线性二次型调节器(Linear Quadratic Regulator,简称LQR)是以状态空间描述的线性系统为被控对象,采用状态反馈形式,兼顾终端状态的准确性、系统响应的快速性、系统运行的安全性及节能性等综合性能指标的一种最优控制策略。
假设线性时变系统
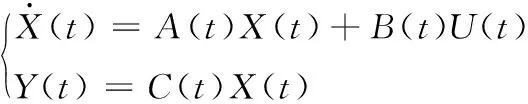
(34)
若取C(t)为单位矩阵,则跟踪误差
e(t)=Yr(t)-Y(t)=Xr(t)-X(t)
(35)
设计状态反馈控制器
U(t)=-K(t)X(t)
(36)
若取性能指标
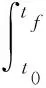
(37)
显然,它是状态变量X(t)和外界控制输入U(t)的二次型函数。这种动态系统的最优化问题称为线性系统二次型性能指标的最优控制问题。其中,Q(t)为正定(或半正定)的状态变量权重矩阵;R(t)为控制变量的权重矩阵,它是正定厄米特矩阵或实对称矩阵
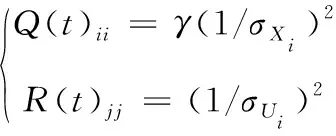
(38)
一般,取R(t)为单位矩阵。γ是两个权重的比值,它是LQR控制的唯一参数。
当J=Jmin时,系统跟踪误差和控制所需能量综合最优。此时,外部输入控制为
U*(t)=-K(t)X(t)=-R-1(t)BT(t)P(t)X(t)
(39)
其中,P(t)是矩阵黎卡提微分方程
+P(t)B(t)R-1(t)BT(t)P(t)-Q(t)
(40)
的对称解。K(t)由正定的对称加权矩阵Q(t)和R(t)共同决定。
4.2 稳定性分析
根据式(23),用机器人学中的“计算力矩”作为控制律[13:
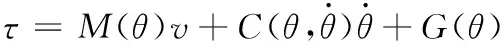
(41)
其中
v=
(42)
关节位置的跟踪误差表示为
e=θ-θd
(43)


(44)
结合式(42)得
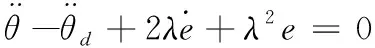
(45)
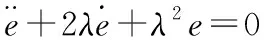
4.3 系统线性化
下肢外骨骼机器人是非线性、高阶次、多变量的系统。根据李雅普诺夫线性化方法,采用LQR控制之前,先要将非线性系统在期望轨迹的平衡位置近似线性化。假设带有控制输入的非自治非线性系统表示为

(46)
根据李雅普诺夫线性化方法,将非线性系统在每个采样点的平衡位置计算雅克比矩阵[13]
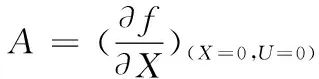
(47)
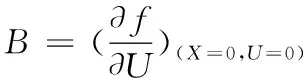
(48)
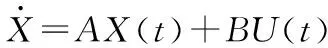
4.4 仿真及实验测试
利用MATLAB/Simulink平台搭建仿真控制系统,用M语言编写仿真程序开展仿真研究[14]。根据人体临床步态分析(Clinical Gait Analysis,CGA) 可知,步行时关节位置的波形近似为正弦波。结合关节运动角度的范围,假设髋关节和膝关节角度的期望输入为
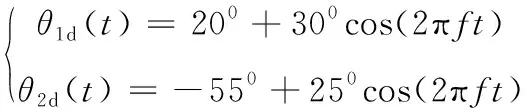
(49)
其中,f=0.1Hz。在LQR控制中,取γ=0.3,σXi=0.0175,σUi=1,仿真得到髋关节和膝关节运动的轨迹分别如图4和图5。经分析可知,基于LQR控制的步态轨迹对整个参考轨迹都能很好地跟踪,而传统PD控制只能实现局部跟踪,且跟踪误差较大。尤其在关节运动的极限位置,LQR控制的跟踪精度比PD控制提高约15%。

图4 髋关节运动轨迹跟踪

图5 膝关节运动轨迹跟踪
为了验证LQR控制在实际外骨骼机器人系统中的控制效果,再进行实验测试。如图1,让使用者穿戴好外骨骼服,选取CGA数据库中行走时人体关节的轨迹点作为控制器的参考输入,经多次反复实验测试,获得大量数据,通过计算机进行数据分析和曲线拟合,绘制出髋关节和膝关节的跟踪轨迹分别如图6和图7。经分析可知,实际外骨骼机器人系统工作正常,关节的运动轨迹光滑,跟踪误差较小。使用者穿戴外骨骼服行走时,关节的动作幅度比正常情况下略有减小,在大腿摆动的初始时刻更加明显。跟踪误差主要来源于人体和外骨骼服的一体化程度不够,以及被动式脚踝的近似处理等,这些方面需要进一步完善和优化设计。

图6 外骨骼机器人髋关节运动轨迹跟踪
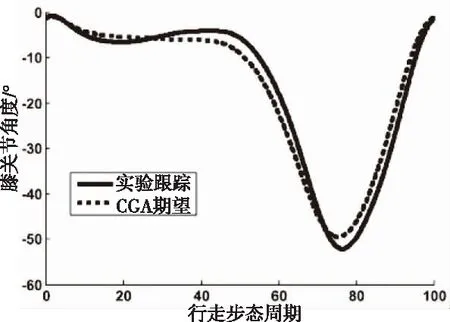
图7 外骨骼机器人膝关节运动轨迹跟踪
5 结束语
关于下肢外骨骼机器人建模和步态轨迹跟踪的研究,得到以下结论:
1)通过牛顿-欧拉公式与系统参数辨识方法建立的人机一体化下肢外骨骼机器人系统的动态模型正确,建模方法有效。
2)基于LQR控制的步态轨迹跟踪误差比常规PD控制更小,跟踪精度更高。
3)研制的下肢外骨骼机器人的机械结构设计合理,控制策略有效,具有辅助行走功能,为相关课题的研究提供了参考。
在后续的研究中,拟采用人工智能算法,完善使用者运动意图识别和运动轨迹规划等功能,优化样机的综合性能,尽快实现产品化和推广应用。

