基于不同调整目标的旋翼动平衡调整研究
纪小苗,杨 茂,宁晨曦
(西北工业大学航天学院,陕西 西安710072)
1 引言
由于制造误差和使用磨损,直升机旋翼系统的各部件不完全相似,导致机体出现显著的1/rev振动,以及旋翼桨叶运动轨迹(锥体)离散。旋翼动平衡(Rotor Track and Balance,RTB)调整就是通过对旋翼系统特定部件施加调整,从而降低直升机机身1/rev振动水平以及桨叶轨迹的离散性。为确保直升机飞行安全以及乘客乘坐的舒适性,若机身1/rev振动或桨叶锥体离散超过一定水平,就必须进行RTB调整。实际应用中,RTB调整包括调整类型、调整位置(即在哪些桨叶上施加)。调整类型有三种:①桨距拉杆长度:改变相应桨叶的总距大小;②配平质量:改变相应桨叶的质量;③后缘调整片偏转角度:改变相应桨叶局部气动力和力矩。
RTB调整实际上是人为制造一个不相似,使其引起的直升机响应抵消原有不相似引起的响应。可见,只有建立调整量与直升机响应(1/rev振动、桨尖轨迹离散性)之间的映射关系才能进行RTB调整。在实际应用中,由于直升机结构和气动环境的复杂性,建立高保真的直升机数学模型非常困难。由于神经网络具有很强的非线性映射能力、自学习和自适应能力和一定的容错能力等优点,只要有合适的输入、输出数据来训练神经网络,就可以用神经网络来代替复杂的直升机数学模型,表示调整量与响应的映射关系。因此基于神经网络的RTB方法得到广泛应用,例如,国外很多直升机上安装的健康和使用监测系统(Health and Usage Monitoring System,HUMS)就采用了神经网络技术[1]。国外学者对直升机RTB系统的数学模型及识别、调整算法进行了深入研究[2-5]。国内在该领域的研究主要是利用神经网络开展旋翼系统故障诊断(包括识别故障类别、位置及程度),神经网络的训练数据来自风洞实验[6-9],或者利用GRNN网络和自适应遗传算法对机身1/rev振动进行单独调整,以降低机身的1/rev振动,但并未考虑振动调整与直升机锥体平衡两者间的相互影响[10][11]。虽然神经网络可以方便地模拟直升机这样复杂的系统,但训练和测试神经网络所需的大量数据的获取是一个巨大挑战。目前来看,训练数据一般是通过试飞获得。试飞方法虽然准确,但存在两个问题:①试飞成本高昂,因此数量有限;②为确保飞行安全,通常不会试飞过大的调整,因此数据范围也受限制。
目前,国内相关研究大多聚焦于旋翼故障识别,采用多层神经网络来识别故障的程度和位置,并非以调整为目的,或者使用多种不同的神经网络来进行这一工作,进而对各神经网络的识别能力进行了对比。有鉴于此,本文采用广义回归神经网络(General Regression Neural Network,GRNN)来模拟RTB调整量与直升机响应的关系,相比于传统的神经网络(如BP网络),GRNN具有收敛速度快、所需样本数量少、人为影响参数少等优点[12][13]。然后利用直升机综合分析程序生成的仿真数据来训练和测试神经网络。分析程序可以模拟任意调整量的响应,相当于扩大了训练数据覆盖范围,由于粒子群-遗传(PSO-GA)混合算法收敛速度快、优化性能好且全局优化能力较高,为寻找最优调整量,本文采用了该算法来提高全局寻优能力[14]。将GRNN网络和PSO-GA算法结合,得到RTB调整算法。该算法可针对三种目标进行寻优:①基于桨尖轨迹;②基于机体1/rev振动;③基于桨尖轨迹和机体1/rev振动。
2 GRNN网络建立
2.1 基础网络
GRNN是径向基网络的另一种变形形式[12]。它建立在非参数回归的基础上,以样本数据为后验条件,执行Parzen非参数估计,依据最大概率原则计算网络输出。本文采用GRNN网络来建立调整量与直升机响应之间的映射关系。GRNN网络由四层构成(图1):①输入层用来接受样本单元;②隐藏层是径向基层,接收来自输入层的数据;③加和层的神经元分为两种:a)分母单元用来计算隐藏层各神经元的代数和;b)分子单元用来计算隐藏层神经元的加权和,权值为各训练样本的期望输出值;④输出层则将加和层的分子单元、分母单元的输出相除,得到网络的估算值Δv。
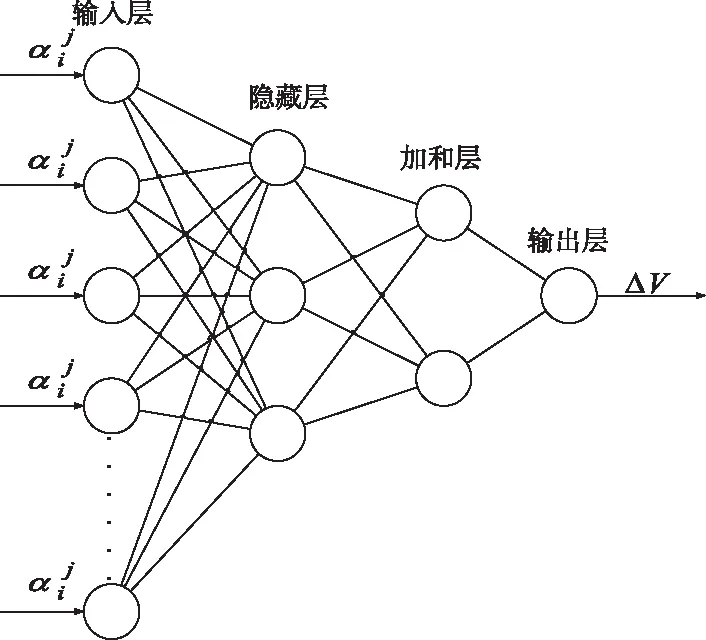
图1 基础网络结构
如图1所示,GRNN网络为多输入、单输出结构。RTB调整包括调整类型和调整位置,因此调整量的数目为3Nb个(3是调整类型数目,Nb是桨叶数目)。由于RTB调整量(输入)和直升机响应(输出)都不止一个,因此要采用多个图2所示的子网络来构建调RTB整量与直升机响应之间的映射关系。为使网络结构描述更清楚,用图2代替图1来表示最基础的一级子网络。图2中,每一个子网络L都有3Nb个输入量,1个输出量。描述调整量与直升机响应映射的网络就是由很多这样的子网络组合而成。
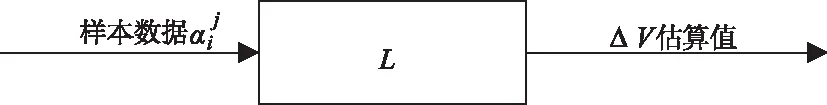
图2 用于RTB调整的一级子网络L
实际应用中,有三种RTB调整目标:①基于桨尖轨迹:使每片桨叶的运动轨迹一致,即桨尖轨迹离散量小于规定值;②基于机身1/rev振动:使机身特定部位的1/rev振动小于规定值;③基于桨尖轨迹和机身1/rev振动:使机身1/rev振动和桨尖轨迹离散均小于规定值。不同的调整目标对应的输入和输出不同,因此它们的GRNN网络拓扑结构也不相同,下面各节分别加以介绍。
2.2 基于桨尖轨迹的网络
基于桨尖轨迹的GRNN网络结构由多个图2所示的子网络构成,每个子网络的输入均为RTB调整量,输出为某一片桨叶的桨尖挥舞偏差。根据桨叶片数和飞行状态,构建出基于桨尖轨迹的GRNN网络模型。
若旋翼桨叶片数为Nb,每片桨叶都有三种调整类型(桨距拉杆长度、配平质量、后缘调整片弯曲角度),因此有3Nb(=Nb×3)个输入量。网络的输出为挥舞偏差Δwi,即

(1)

RTB调整要保证在整个包线内有效,因此在实际应用中通常取四种速度(地面开车、悬停、巡航速度、最大前飞速度)进行试飞,这里用Vj(j=1,2,..Nv,Nv分别对应这四个速度)来表示。因此,以图2所示一级子网络L为基础,构建出图3所示的二级子网络P。它的输入是某一速度Vj下的旋翼调整量,输出是整个旋翼的挥舞偏差(Nb个)。然后以四个二级子网络P组成的GRNN网络(图4),用来模拟整个速度包线内,RTB调整量(输入)与桨尖轨迹偏差的映射关系。

图3 某一速度下的二级子网络P
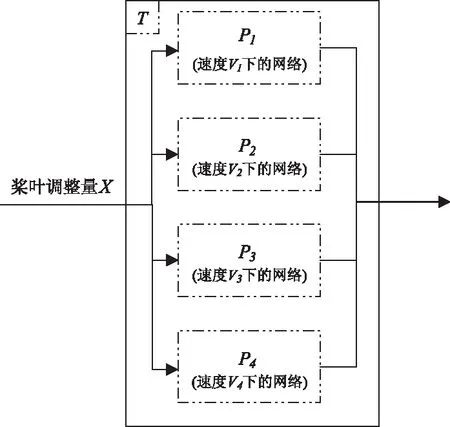
图4 基于桨尖轨迹的网络模型T
2.3 基于机身振动的网络
在建立RTB调整量与机体1/rev振动的映射关系时,最基础的GRNN网络结构与图1相同,输入为RTB调整量,有3Nb(Nb是桨叶数目,3是调整类型)个分量,但输出为特定位置的机体振动矢量的某一分量。由于振动为矢量,这里用其正弦和余弦分量表示。也就是说,机身某一点的1/rev振动需要两个图2所示的基础网络来表示。
在实际应用中,通过监测机身Np个测点处的1/rev加速度矢量来评估旋翼动平衡情况。RTB调整要保证在整个包线内有效,在实际应用中通常取四种状态(地面开车、悬停、巡航速度、最大前飞速度)进行试飞,这里用Vi(i=1,2,..NV,NV=4分别对应这四个速度)来表示。图5显示了某一速度下,机身Np个测点的1/rev加速度的正弦和余弦分量所构成的二级子网络U的结构。该U网络由2×Np个图2所示的一级子网络L所组成。然后以四个二级子网络U组成的GRNN网络(图6),用来模拟整个速度包线内,RTB调整量(输入)与机身1/rev振动(输出)之间的映射关系。
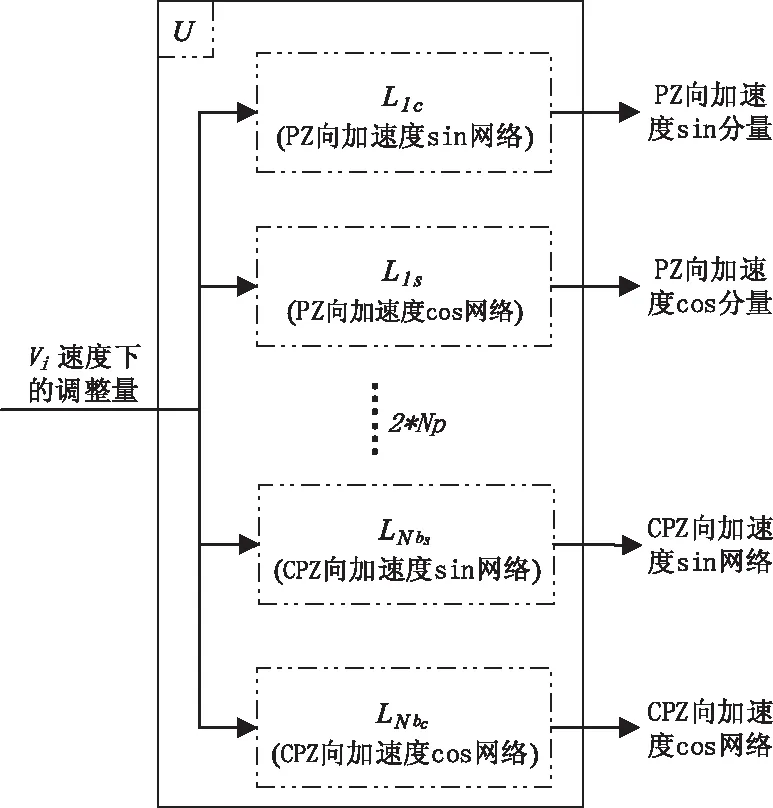
图5 某一速度下的二级子网络U
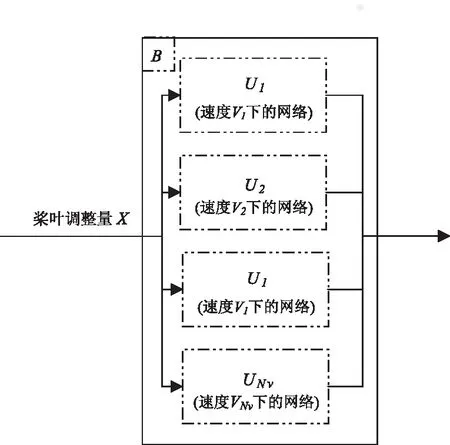
图6 基于机体振动的网络模型B
2.4 基于桨尖轨迹和机体振动的网络
对于同时考虑桨尖轨迹和机体1/rev振动来进行RTB调整的情况,需要分别采用最基础的GRNN网络(图2)模拟各飞行状态下桨叶调整与桨尖轨迹和机体1/rev振动间的映射关系。为保证RTB调整在整个包线内有效,取与前两种调整方案相同的四种状态(地面开车、悬停、巡航速度、最大前飞速度)进行试飞。由于已经分别构建好了RTB调整量与机体1/rev振动(基于机体振动的网络模型B)和桨尖轨迹偏差(基于桨尖轨迹的网络模型T)间的映射关系,因此 RTB调整量(输入)与机身1/rev振动和尖轨迹偏差(输出)之间的映射关系如图7所示。
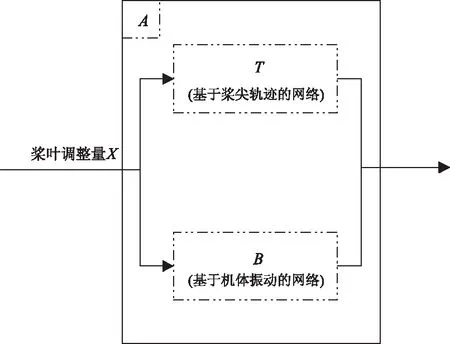
图7 基于机体振动和挥舞偏差的网络模型A
3 RTB调整寻优算法
RTB调整的实质是对旋翼系统施加一组新的不相似(调整),使其产生的响应可以抵消/减小旋翼原有不相似引起的响应。由于这样的组合不唯一,因此需要采用寻优算法获得最佳方案。在求解复杂优化问题时,遗传(GA)算法具有较好的全局优化能力,但计算效率较低,收敛速度较慢;而粒子群(PSO)算法收敛速度快、局部优化能力强,但全局搜索能力较差。两者结合可以继承各自优点,克服不足,提高算法计算效率和全局寻优能力[8][9]。本文采用PSO-GA算法作为RTB调整优化算法,以提高优化效率并获得较好的全局优化。
图8给出了RTB调整算法的整体流程。首先为算法提供输入数据,然后根据判定条件确定是否需要进行RTB调整,当需要进行调整时,随机生成初始种群,将初始种群带入到相应的GRNN网络中得到输出值,将网络输出值带入到适应度函数中计算适应度值,然后将适应度值带入到PSO-GA算法中,找出当前群体最优解,当满足终止条件时,输出调整方案。本文以迭代次数作为判定条件,当完成给定的迭代次数后,认为寻优完成。
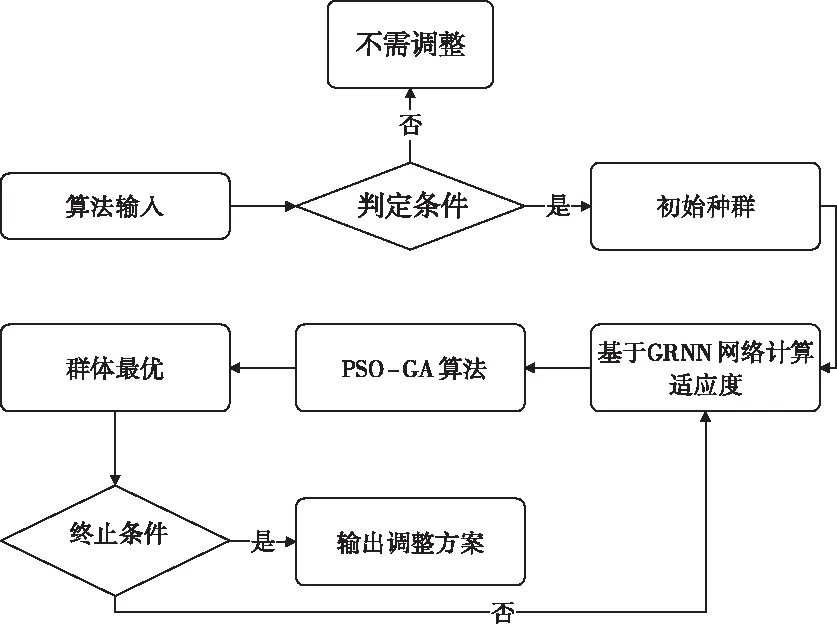
图8 RTB调整流程
3.1 PSO-GA算法
RTB调整算法是通过PSO-GA算法与GRNN网络相结合,其中PSO-GA算法是参数寻优的主体,GRNN网络为PSO-GA算法中的适应度函数提供数据。对于不同的RTB调整算法,其差异主要在于GRNN网络的模拟对象、算法输入及算法适应度函数不同。
GRNN网络通过样本数据的训练,可以模拟整个调整空间与响应空间的映射关系,即训练完成的GRNN网络可以对调整范围内的任意输入计算出其相应的输出值,也就是桨叶上所要施加的调整量,即

(2)
其中,X表示整个解空间,z为扰动下的测量数据yi与GRNN网络模拟差f(xi)的差,δ为一小量,当z<δ,则xi为可能解,当z≥δ则xi不是该状态下的解。
在调整量优化中,训练好的GRNN网络对多个输入不满足线性叠加的假设,即f(X)≠f(a)+f(b)。因此需要进行变换。首先对输入量X进行变换,即将
X=[ab0 0]
(3)
变为
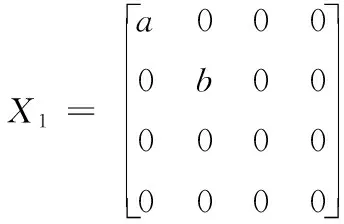
(4)
将X1的每行分别带入到f(x)中,然后相加,即可得到f(X)≠f(a)+f(b)。
3.2 适应度函数
适应度函数是优化算法中不可缺少的一部分,是优化算法中选择最优个体的重要依据。RTB调整算法用到了三个不同的GRNN网络(图4、图6和图7),因此要建立对应的适应度函数。
当基于桨尖轨迹调整时,目标是使动平衡调整后在所有(四种)飞行状态下的桨叶挥舞偏差最小。因此是一个多目标优化问题,需要对各目标函数进行协调,从而得到全局最优方案。基于桨尖轨迹的RTB调整的目标函数为
(5)
式中,ZTi为网络T得到的模拟值YTi与扰动下的桨叶挥舞偏差TTi的误差绝对值,yT是目标函数,也是PSO-GA算法的适应度函数,yT越小,说明对应的调整产生的桨叶挥舞偏差与输入值越相近。优化算法会选择每代种群中适应度值最小的个体作为最优个体参与到下一次迭代中。迭代结束后的调整方案是在相应桨叶上去掉调整量,反之说明施加的调整无法减小桨叶挥舞偏差,也不会被优化算法选中,从而被淘汰掉。
当基于机体振动进行RTB调整时,动平衡调整的目标是要使直升机在各飞行状态下的1/rev加速度最小。振动最小的目标函数是在不同飞行状态下,各方向(横向、垂向和纵向)振动的综合反映。也属于多目标优化问题。基于机体振动RTB调整的目标函数为

(6)
式中,ZBi为网络B得到模拟值YBi与扰动下的1/rev加速度TBi的矢量和,yB为目标函数,也是PSO-GA算法的适应度函数,yB越小,说明调整产生的机体振动与输入值越相近,优化算法会选择每代种群中适应度值最小的个体作为最优个体参与到下一次迭代中,迭代结束后的调整方案是在相应桨叶上加上调整量,反之说明施加的调整无法减小机体振动,也不会被优化算法选中,从而被淘汰掉。
当同时考虑桨尖轨迹和机体1/rev振动时,目标函数由两部分组成,第一部分对应的是桨尖轨迹,第二部分对应的是机体振动,目标函数是两者的加权和,如下所示

(7)
式中,ZTi为网络T模拟值YTi与扰动下的桨叶挥舞偏差TTi的误差绝对值,yT是所有飞行状态下各片桨叶误差绝对值之和;ZBj为GRNN网络模拟值YBj与输入1/rev加速度TBj的矢量和,yB是所有飞行状态下各测量点加速度矢量和之和;yR则表示同时考虑了桨尖轨迹和机体1/rev振动,a是桨尖轨迹加权系数,b是机体1/rev振动加权系数,两者之和为1,由于RTB调整的主要目的是降低机体1/rev振动,因此b>a,yR越小,说明对应的调整越接近最优解。
3.3 约束
RTB调整后,各点振动加速度值v应小于规定值Lv,即
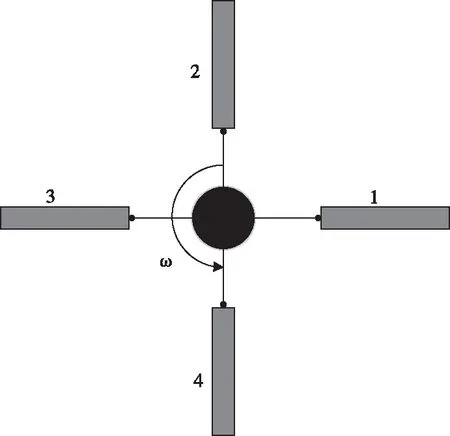
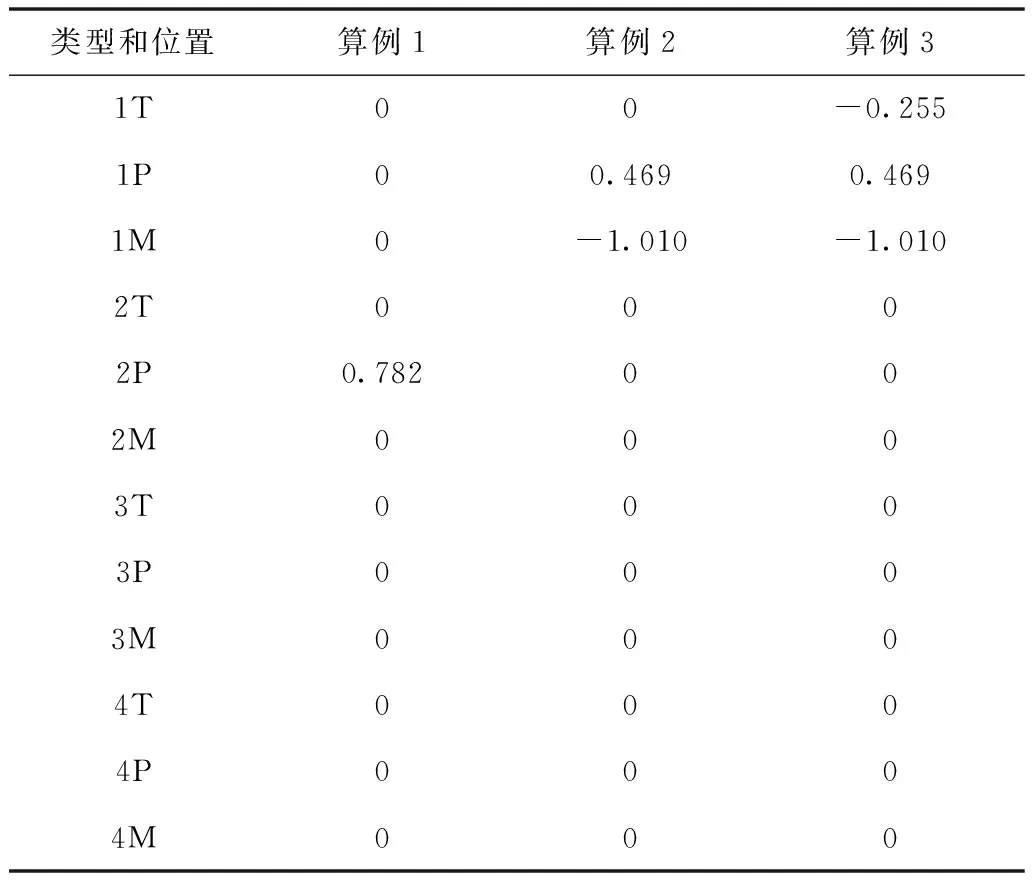
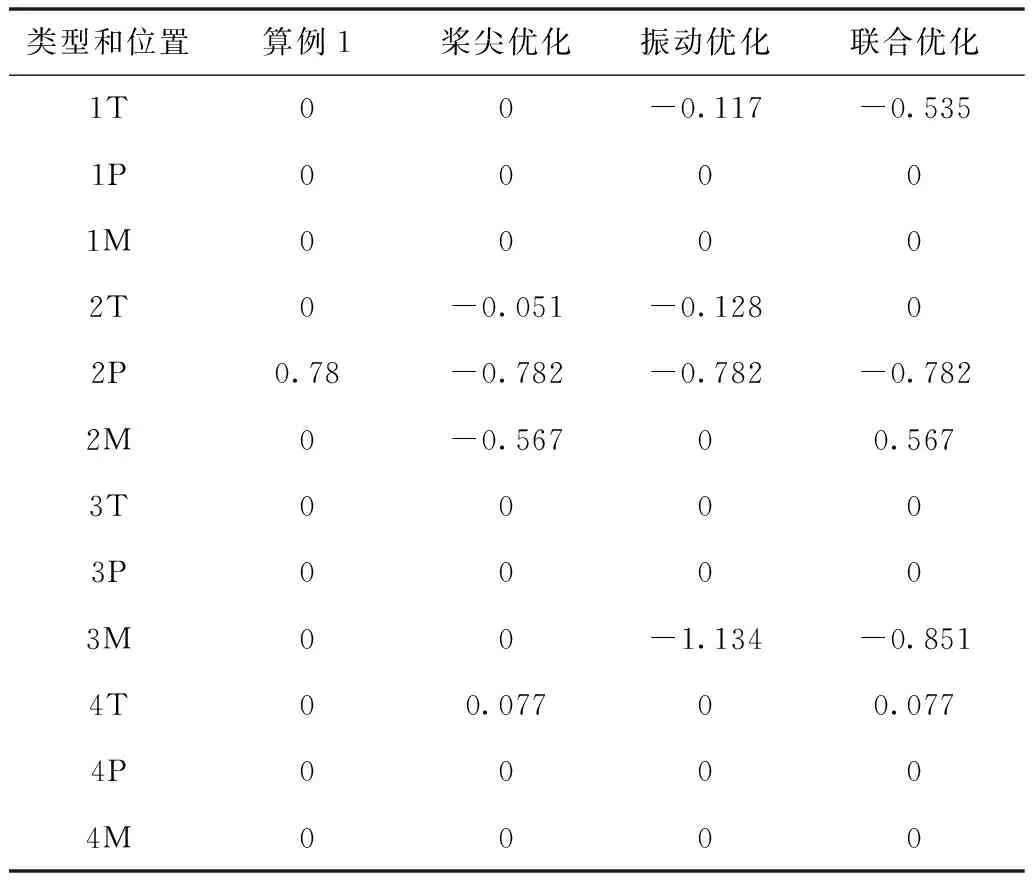
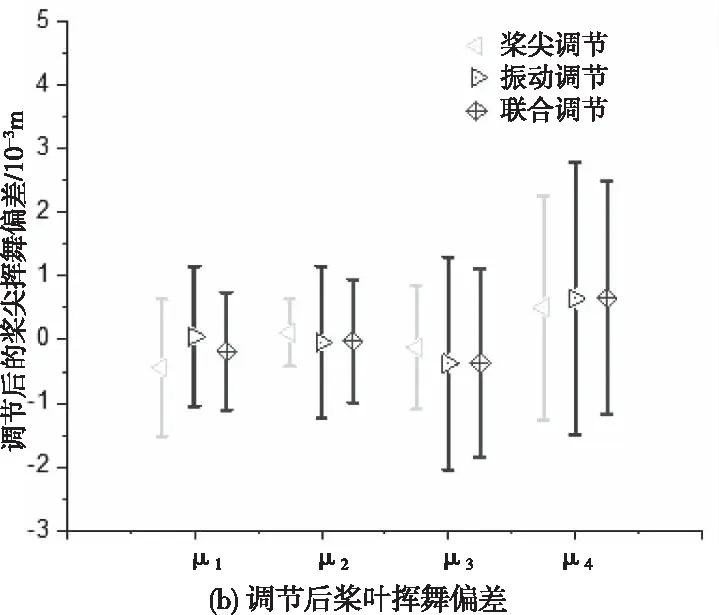
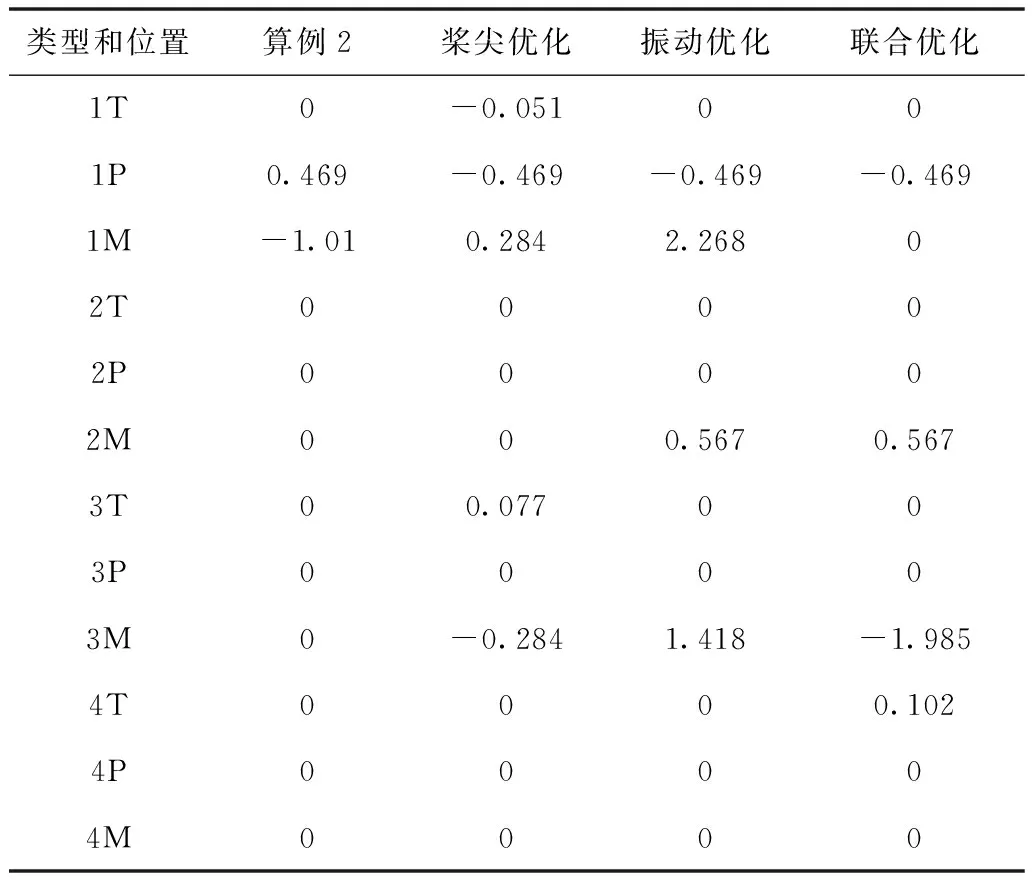
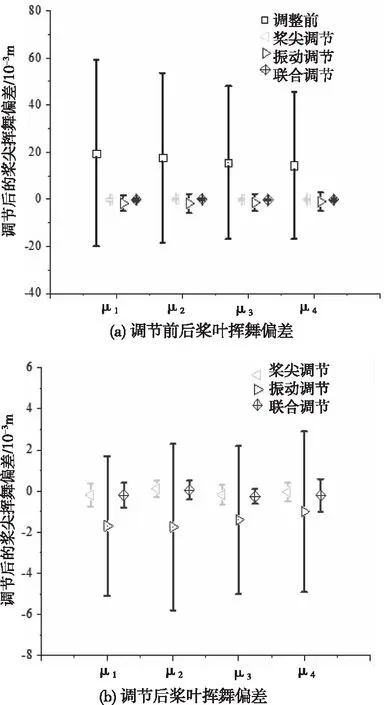
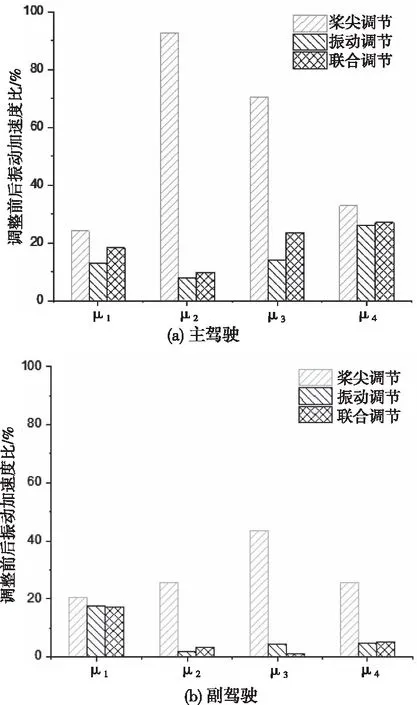
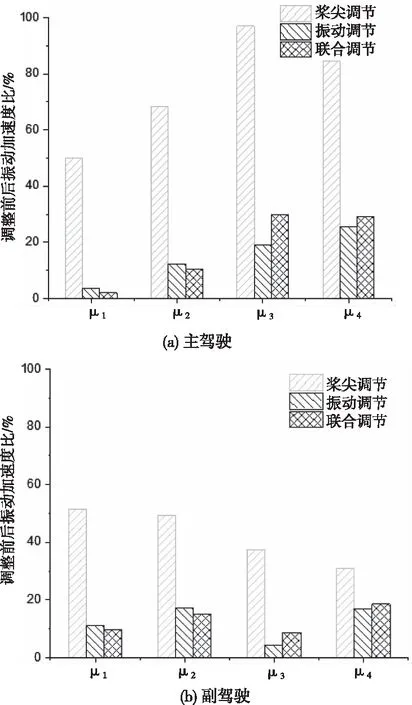
v (8) RTB调整后,桨叶挥舞偏差d应小于规定值Ld,即 D (9) (10) 由于用于神经网络训练的试飞数据有限,故本文基于文献[14][15]中的直升机综合程序和3种扰动方式(表1),采用某四叶旋翼的直升机及其机身有限元模型,分别模拟了包线内若干飞行状态下直升机旋翼桨尖偏量和机身1/rev加速度。由于直升机综合程序无法模拟地面开车状态,故模拟了四种前飞状态的全机动响应,如前进比μ1=0(悬停状态),μ2=0.1(79 km/h),μ2=0.2(159km/h)和μ2=0.25(198 km/h),并将其作为神经网络的训练数据。为简化描述,下文中,用T代表TAB(后缘调整片调整),P代表PCR(桨距拉杆调整),M代表MASS(配平质量调整)。桨叶编号如图9所示。表2给出了动平衡调整算法在不同调整类型下的调整范围。 图9 桨叶编号 表1 扰动类型及情况 表2 旋翼动平衡调整范围 由于有四种飞行状态(Nv=4),旋翼有四片桨叶(Nb=4),机身振动测点3个(Np=3)因此,基于桨尖轨迹动平衡调整共需16个基础L网络(图3、4),基于机体振动的动平衡调整需要24个基础L网络(图5、6),基于桨尖轨迹和机体振动的联合调整需要40个基础L网络(图2、7)。计算时PSO-GA算法的参数为:种群大小为100;迭代次数为500;PSO算法的学习因子c1和c2均为2;采用自适应的交叉和变异概率。 首先采用单一扰动(算例1)对RTB算法进行验证。对桨叶2施加PCR扰动,并利用仿真程序得到相应的机体1/rev振动值和桨尖挥舞偏量,然后将所得到的值作为RTB算法的输入,来验证算法准确性,并对优化结果进行分析。 表3为采用三种不同的动平衡调整算法给出的最优调整方案。与初始扰动量对比可知,三种方案都可以准确识别扰动,且基本可以消除原有扰动,但由于三种调整算法的适应度函数及约束等不同,故调整方案存在一定差异。 表3 单一扰动和各种调整方案 图10给出了不同前进比下锥体调整前后的挥舞偏差比。结果显示,三种调节方案均可使桨叶挥舞偏差降低90%以上,且桨尖调节方案稍优于其它两种方案,联合调节方案次之,振动调节的方案最后。 图10 不同前进比下锥体调整前后的挥舞偏差 图11给出了不同前进比下,主、副驾驶处调整前后的1/rev振动水平比。结果显示,振动调节和联合调节两种方案效果相近,且可使不同前进比下的振动水平降低80%以上,而采用桨尖调节的振动水平仍相对较高,前进比为c2时,主驾驶处的振动水平降幅仅有45%左右,远低于其它两种方案。图10和图11中三种方案的效果差异是由于优化目标差异造成的。 图11 不同前进比下主驾驶、副驾驶处调整前后振动水平比 表4显示了对桨叶1施加PCR和Mass复合扰动(表1中算例2),以及三种调节算法给出的最优调整方案。与初始扰动相对比可知,3种调节方式都可以将PCR扰动完全消除,但在质量调整方面有较大差异。 表4 复合扰动和各种调整方案 从图12给出了不同前进比下锥体调整前后的挥舞偏差比。结果显示,三种调整方案都显著降低了桨尖挥舞偏差。不过,桨尖轨迹调整方案与联合调整方案效果相近,且都优于振动调整方案。 图12 不同前进比下锥体调整前后的挥舞偏差 图13给出了不同前进比主、副驾驶调整前后的振动水平比。结果显示,三种方法都能降低主驾驶和副驾驶处的1/rev振动水平。不过基于桨尖调整的方案效果明显不如另外两种。基于振动调节和联合调节这两种调节方式减振效果相似。 图13 不同前进比主副驾驶调整前后的振动水平比 表5显示了对桨叶1所施加的Tab、PCR、Mass复合扰动(表1算例3),以及三种调节算法给出的最优调整方案。结果显示,3种调整方案都可以较好地抵消原始扰动,不过3种方法给出的具体调整方案有差异,效果需要进一步分析。 表5 复合扰动和各种调整方案 图14给出了不同前进比下锥体调整前后的挥舞偏差比。结果显示,三种方案都使桨尖轨迹偏差减小,但基于桨尖轨迹的调整方案远远优于另两种方案。联合调整方案稍稍优于基于振动的调节方案。 图14 不同前进比下锥体调整前后的挥舞偏差 图15给出了不同前进比主、副驾驶调整前后的振动水平比。结果显示,三种方案都使机身1/rev振动水平降低。基于振动的调节方案减振效果最佳,其次是联合调整方案,最后是基于桨尖轨迹的调整方案。 图15 不同前进比主副驾驶调整前后的振动水平比 上述效果差异的原因在于基于桨尖轨迹的调整方案其优化目标并未考虑机身振动,因此减振效果最差。同理,基于振动的调整方案其优化目标没有考虑桨尖轨迹,因此对于桨尖轨迹的调整效果最差。联合调整方案兼顾两者,因此效果介于两者之间。但由于优化目标更多,会导致计算量大大增加。 本文利用GRNN网络来模拟RTB调整空间与直升机响应空间的映射关系,然后将其与PSO-GA算法相结合,形成RTB调整算法。最后通过仿真数据来检验RTB调整算法的有效性。研究得到以下结论: 1)本文的RTB调整算法可以较好的识别扰动的类别、位置和程度,并对其进行有效的调整。 2)在进行RTB调整时,调整方案应与调整目标相匹配,即如果以减小桨尖轨迹偏差为目标,则应选取基于桨尖轨迹的调整方案;若以减小机身1/rev振动为目标,则应选取基于机身振动的方案。 3)如果同时考虑桨尖轨迹和机体振动水平,则RTB调整算法可以有效降低机体1/rev振动水平和各片桨叶的挥舞差值。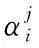
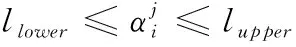
4 结果与分析
4.1 仿真数据

4.2 单一扰动的调整


4.3 复合扰动的调整


5 结论

