基于交通流仿真的多指标航段结构研究

胡莘婷，戴福青，庞笔照

(1. 中国民航大学空中交通管理学院，天津 300300；2. 南洋理工大学机械与航空学院，新加坡 639798)

1 引言

航路网络是空域结构的重要构成要素。其作为一个整体系统，由航路和航路点构成，不同的航路点将航段连接形成网络。纵横交错的航路网络作为空中交通的虚拟路网载体，对空中交通流安全高效地运行以及空中交通运输成本起决定性作用[1]。深入研究空域结构最基本的构成要素，揭示航路结构对空中交通运行的影响机制，在此基础上，有助于开展更为复杂的航路网络规划研究。

目前国内外对于航路结构的研究集中在以下几个方面：关注于航路点位置布局优化[2-4]和交叉点角度结构设计和优化的研究[5-7]，从复杂网络角度对航路抗毁性和脆弱性进行的分析[8-10]，基于空中交通流的航路结构分析与优化[11-13]，以及从空域资源利用率角度对航路结构的研究[14-18]。已有研究虽与航路结构相关，但较少探讨航段结构本身对空中交通运行的影响。本文系统性地研究了航段类型及长度对航空器的活动以及航空器之间相互制约的影响程度，建立了基于空中交通流量的三种航段长度优化模型，通过交通流仿真，对航段长度进行定性及定量的研究，并从飞行时间、燃油消耗、经济价值、机型特征、飞行冲突、管制员工作负荷等多指标评价优化结果。

2 空域结构的基本构成要素

2.1 航路点

常见的航路点有两种，航路节点 (Air Route Network Nodes，ARNN) 和航路交叉点 (Crossing Waypoints，CWP)，如图1所示。不同方向的航段在交叉处产生航路交叉点，交叉点最大的作用是改变航路走向，使经过该点的航空器改变航向；除了交叉点以外的航路点为节点，其大多为管制扇区的边界点，往往有着扇区准入高度和速度的限制条件。航空器在航路点处常会做出机动动作，如改变航向、变换高度层等；当交通流过于密集时，为满足航空器之间最小安全间隔标准、避免飞行冲突，管制员会指挥有潜在飞行冲突的航空器调整速度、改变航向、变换高度层，或盘旋等待，直到飞行冲突解脱为止。

图1 航路点

2.2 航段结构

航路点之间直接相连构成航段，航段的类型和长度由航路点决定。航空器在空中飞行除了要满足基本的安全间隔要求以外，还需满足众多航路点不尽相同的空中交通限制条件，如过点高度限制、流量限制、时间限制等。在复杂的高密度空域环境中，航段的类型及长度会影响空中交通运行的安全和效率。航路点之间距离越近，航段长度越短，各航路点的相关限制因素越密集，航空器之间的相互制约程度越大，致使航空器的机动飞行受阻，造成空中交通拥塞及延误。同时，航空器有改变航向、飞往不同目的地的需求，航段长度无法无限长。且不同类型的航段组合受交通流分布的影响，也会产生相互制约长度的效果。因此，一条航路中各类型的航段存在最优长度组合是本文研究的理论基础。由不同的航路点直接相连构成的3种航段类型如图2所示。

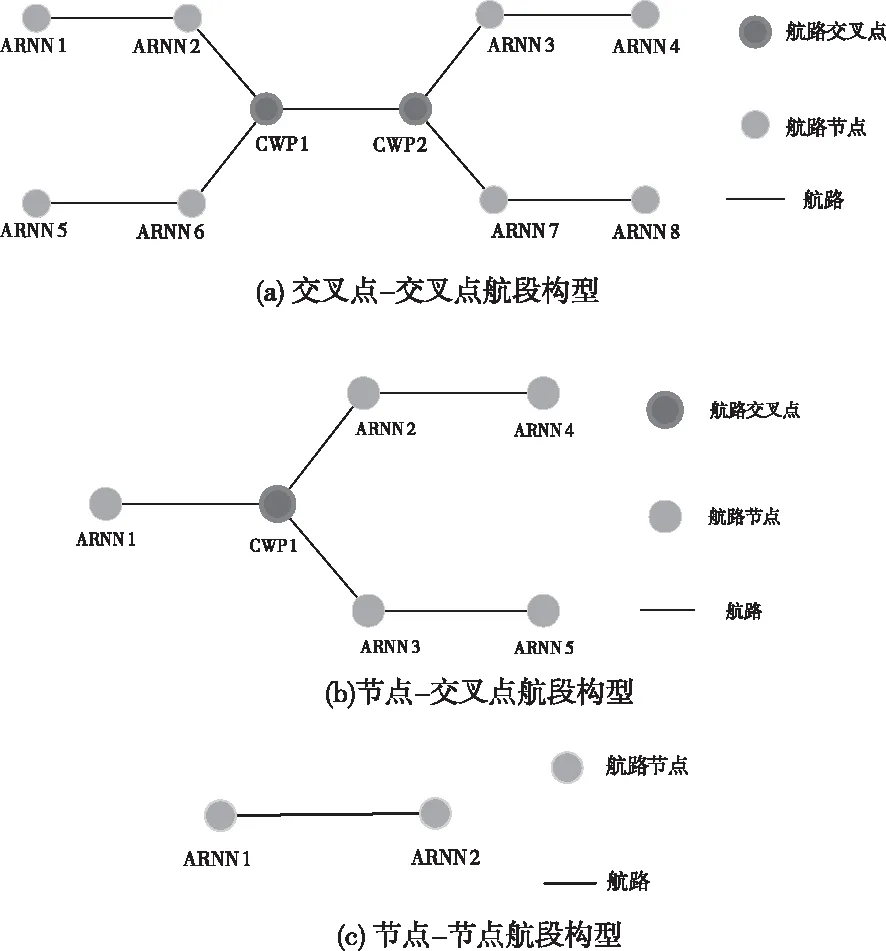
图2 航段类型

3 飞行时间及燃油消耗与航段长度的关系

3.1 输入数据

本文采用计算机仿真的方法，利用全空域仿真软件Total Airspace and Aerodrome Modeler (TAAM) 进行仿真。为保证仿真结果的合理性和普适性，采用与实际运行相同的管制规则，选取国内某早高峰时段的真实航班计划数据100条，其中宽体飞机、窄体飞机、支线飞机按2018年民航全行业运输飞机期末在册架数取为0.12∶0.83∶0.05。

3.2 设计仿真

仿真采用控制变量法，固定航段相交角度和航路总飞行距离不变，分别研究各类型航段长度对空中交通流的影响。3种航段类型均按航段长度由10km至160km变化，每隔10km进行一组实验，每种航段类型各进行16组，共实验48组。仿真结果及拟合函数结果如下。

图3为单位航班飞行时间随交叉点-交叉点航段/节点-交叉点航段长度的变化关系。

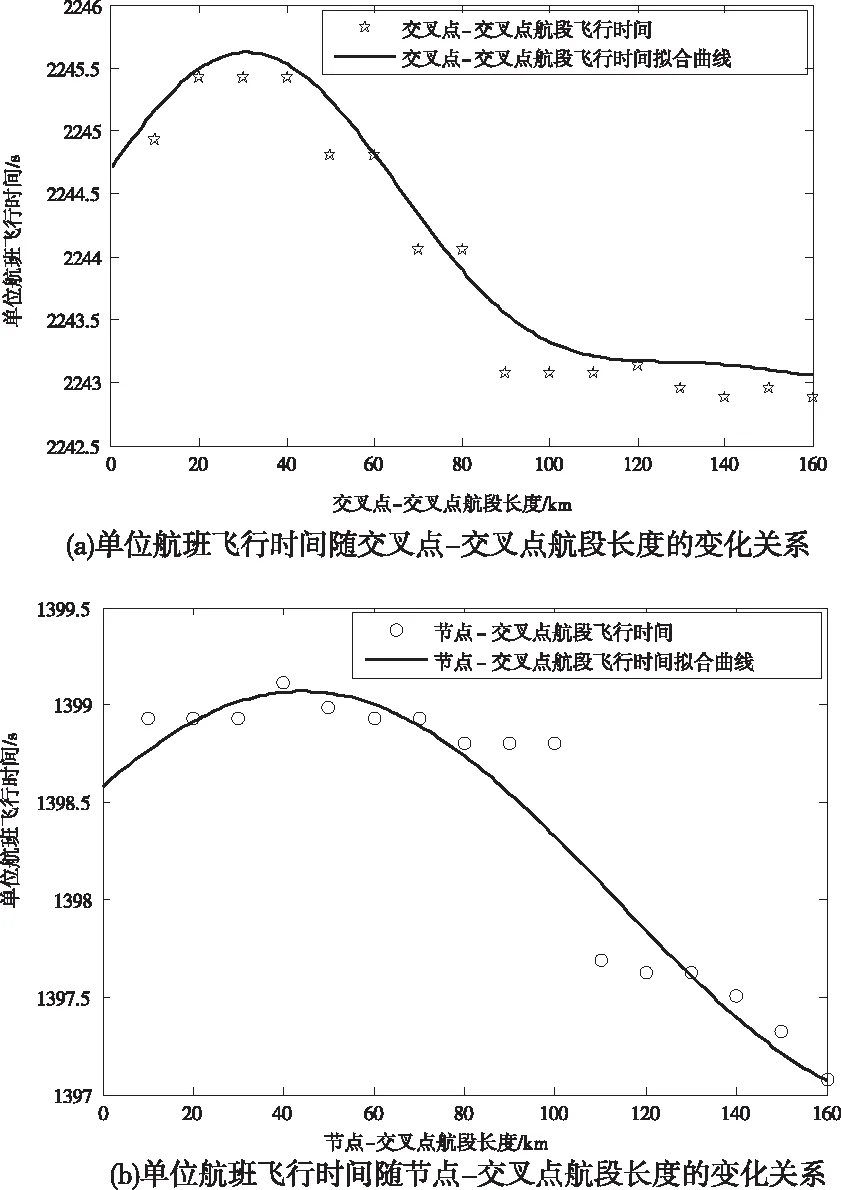
图3 单位航班飞行时间随交叉点航段长度的变化关系

当交叉点之间距离小于40km时，航班飞行所需时间较长；随着交叉点之间距离的增大，单位航班飞行时间逐渐减小，90km后对飞行时间几乎无影响。

当节点-交叉点航段长度小于100km时，单位航班飞行时间激增，说明节点-交叉点航段长度小于一定阈值时，两个航路点之间的不利影响会迅速增加。

图4单位航班燃油消耗随交叉点-交叉点航段/节点-交叉点航段长度的变化关系。

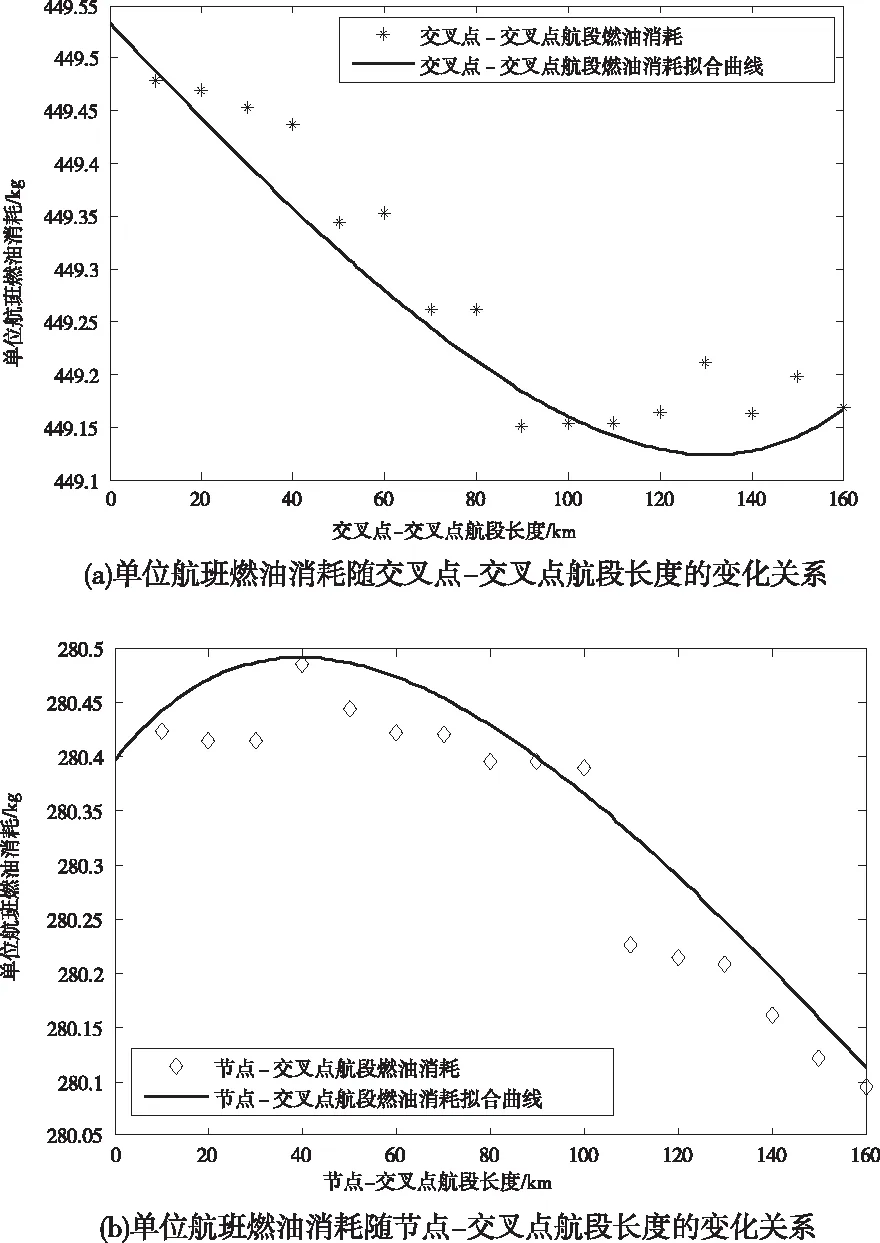
图4 单位航班燃油消耗随交叉点航段长度的变化关系

当交叉点之间距离由90km至40km逐渐靠近时，单位航班燃油消耗变化较为明显；剔除实验异常点对曲线进行拟合，发现航段长度大于90km时航段长度改变对燃油消耗几乎无影响。

单位航班燃油消耗与飞行时间类似，当节点-交叉点航段长度小于100km时，单位航班燃油消耗激增，说明节点-交叉点航段长度小于一定阈值时，空中交通流的通畅程度降低。

仿真结果表明，节点-节点航段长度不影响空中交通的运行效率，符合常理。因该类型航段附近无交叉点，无需为此做出机动动作以避免飞行冲突，该航段的交通流运行呈畅行态。

为了进一步明确飞行时间及燃油消耗随不同航段类型及长度的变化关系，本文对上述关系进行函数拟合，选取令人满意的拟合结果，得到非线性函数关系表达式如下：

1)通过交叉点-交叉点航段/节点-交叉点航段的单位航班飞行时间函数关系式分别为

tCWP-CWP(x)=2244+0.7481 cos(0.02854x)+0.9947 sin(0.02854x)-0.04303 cos(0.05708x)+0.3809sin(0.05708x)

(1)

tARNN-CWP(y)=1398+0.5775cos(0.02266y)+0.9015sin(0.02266y)

(2)

2)通过交叉点-交叉点航段/节点-交叉点航段的单位航班燃油消耗函数关系式分别为

fCWP-CWP(x)=449.5e(-1.161E-05)x+0.03346e0.01692x

(3)

fARNN-CWP(y)=281e(-1.901E-05)y-0.6032e0.01795y

(4)

式(1)到式(4)的函数拟合精度分别达到了0.9774、0.9307、0.9269和0.94444.通过采用典型的航班计划和相同的空域环境、管制规则，得到的单位航班飞行时间及燃油消耗随不同航段类型及长度的变化结果，并进一步拟合成函数关系式，对其它空域结构具有一定的适用性，下文将对其进行验证。

4 考虑航班量的航段长度优化模型

一条航路是由多个航段直接相连组合而成，包含交叉点-交叉点航段、节点-交叉点航段和节点-节点航段3种航段类型的共同特性，单位航班飞行时间及燃油消耗随3种航段类型长度的变化关系依然具有适用性。本文对其最小的单位组成进行综合建模，表示如图5所示。

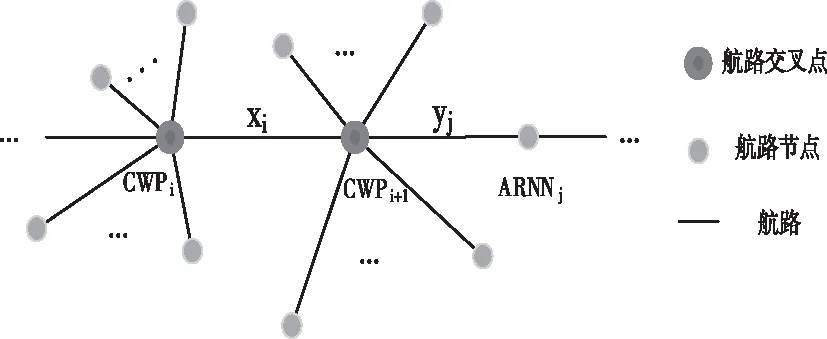
图5 多航段类型的基本构型

固定一条直线航路首、尾航路点的位置，沿直线移动航路中间的点，以改变各个航段的长度。提出在考虑交通流量大小时的3种航段长度优化模型，使流量越大的航段长度越优，达到综合优化的目的。

4.1 目标函数

4.1.1 最小化航班总飞行时间

minT=∑i∈I∑j∈J(Ni*tCWP-CWP(xi)+Nj*tARNN-CWP(yj)

(5)

式中，xi、yj分别表示第i段交叉点-交叉点航段和第j段节点-交叉点航段的航段长度；Ni、Nj分别表示经过第i段交叉点-交叉点航段和第j段节点-交叉点航段对应的航班数量；I、J分别表示所有经过交叉点-交叉点航段和节点-交叉点航段的航班集合。

4.1.2 最小化航班总燃油消耗

minF=∑i∈I∑j∈J(Ni*fCWP-CWP(xi)+Nj*fARNN-CWP(yj)

(6)

4.2 约束条件

1)交通量守恒

Nin=Nout

(7)

进入实验航路的航班总量与离开实验航路的航班总量相等。

2)航段长度范围约束

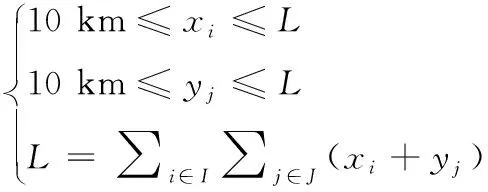
(8)

式中，各航段长度下限为10km，上限L表示航路总长度。

3)容量约束

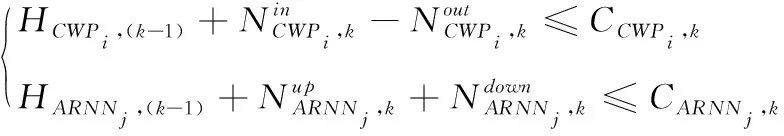
(9)

5 仿真分析

5.1 空域结构和交通流数据

选取国内某典型直线航路，该航路由4个航段组成，其中交叉点-交叉点航段、节点-交叉点航段各2段，共涉及22条不同的飞行路径；交通流数据选取国内2016年10月某一天的航班计划，当日飞经该航路的航班共有497架次。采用TAAM仿真软件进行实验，输出仿真结果并对其进行分析。

5.2 仅优化飞行时间或燃油消耗的结果

根据式(5)和式(6)求得的最优航段长度，依照原始航路结构设计仿真空域结构，采用与原始航路相同的航班计划和交通规则，进行仿真。统计结果如表1所示。

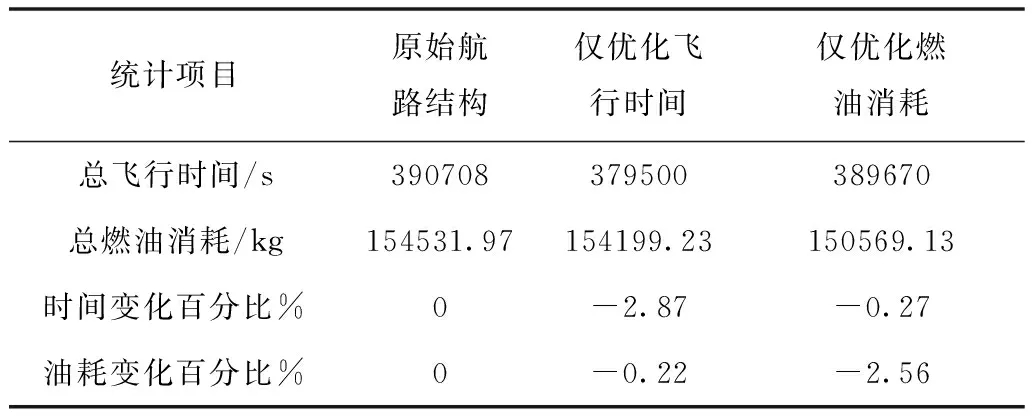
表1 不同侧重对象的优化结果

目标函数为仅优化飞行时间时，优化后的航班总飞行时间减少2.87%，总燃油消耗降低0.22%；目标函数为仅优化燃油消耗时，优化后航班总飞行时间缩减0.27%，总燃油消耗降低2.56%。可知，分别考虑时间或油耗时都可对原始航段长度进行不同程度的优化，但两个优化目标无法兼顾。

5.3 综合优化时间及油耗

为综合评价时间和油耗两个优化指标，定性和定量的研究二者对航路结构的影响程度，统一二者计量单位为其价值，引入成本指数的概念。成本指数为时间成本与燃油成本的比值，根据已有研究[19]，考虑环保的要求，成本指数取CI=22kg/h，油耗成本CF=6.01元/kg，时间成本CT=132.22元/h。

通过引入成本指数，将不同的优化对象结合起来，以其成本价值衡量优化结果。添加评价指标

C=(CTT)/3600+CFF

(10)

综合优化飞行时间和燃油消耗时，优化问题为两个目标函数总飞行时间最小化和总燃油消耗最小化的多目标优化问题。本文采用带精英策略的非支配排序遗传算法(NSGA-Ⅱ)对其进行模型求解。设置遗传算法基本参数为种群规模200，交叉概率0.6，变异概率0.01，终止进化代数500。

对求解结果取均值，再次设计仿真，对比各优化方案的结果如表2所示。

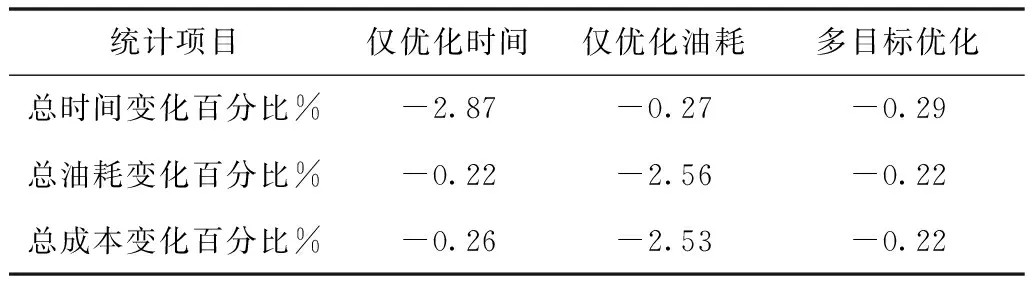
表2 各优化方案结果对比

通过引入经济价值评价指标，可以看出，燃油的经济价值比时间价值高，对总成本的影响最大，对航路结构的优化效果也影响最大。在综合优化飞行时间和燃油消耗时，应优先考虑油耗的影响。

5.4 基于航空公司角度的航空运输结果分析

航空公司作为在市场经济中表现活跃的具有商业性质的企业，对航空运输的效率与效益要求很高。当追求效率最大化时(如需抢占市场份额时)，期望缩减单位航班飞行时间，增加航空器每日的执飞次数，使每架航空器的日利用率最大化；当追求利润最大化时，需缩减燃油成本的支出，提高净利润率。又考虑到不同的航空公司，机队规模不同，故本文从机型划分的角度，进一步细化分析。

5.4.1 飞行时间结果分析

当航空公司追求航空器运行效率最大化时，关注点在单位航班飞行时间。以飞行时间最少对应的最优航段长度设计仿真，结合航空公司不同的机队特征，分析不同机型对应的飞行时间优化结果，如图6所示。

图6 各机型飞行时间优化效果

当优化目标为最小化飞行时间时，窄体机型(A320、B737、B757)的飞行时间平均优化效果约6.95%，宽体机型(A330、B747、B767、B777)的飞行时间平均优化效果约1.64%，优化结果良好，可缩减单位航班飞行时间，提高航空器的利用率。

5.4.2 燃油消耗结果分析

燃油成本是航空公司一项较大的成本支出，当航空公司追求效益最大化时，为了达到盈利目的，旨在削减燃油成本。以仅优化油耗为目标函数对应的最优航段长度为例，结合航空公司不同的机队特征，分析不同机型的燃油消耗优化结果，如图7所示。

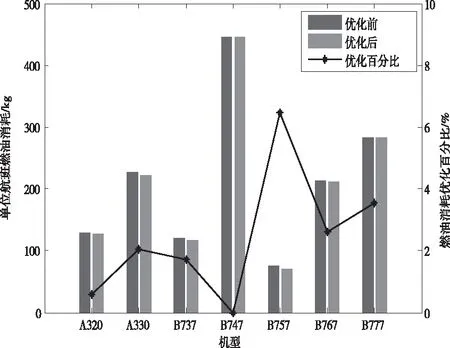
图7 各机型燃油消耗优化效果

当优化目标为最小化燃油消耗时，窄体机型(A320、B737、B757)的燃油消耗平均优化效果约2.91%，宽体机型(A330、B747、B767、B777)的燃油消耗平均优化效果约2.05%，优化结果良好，能够达到节能减排的效果。

5.5 基于空中交通管理角度的交通保障结果分析

民航运输三大主体——航空公司、空中交通管制单位、机场，业务侧重点各不相同。空管单位非商业性质，不以盈利为目的，而以保障空中交通的安全运行为第一目标。空中交通管制员作为直接指挥航空器的人员，肩负巨大的安全保障压力，其工作负荷和工作表现直接关乎空中交通能否安全、高效的运行。因此，基于空中交通管理的安全保障任务要求，本文从飞行冲突和管制员工作负荷两方面进一步细化分析。以总成本最小时的航段长度优化方案为例，飞行冲突和管制员工作负荷在航段长度优化前、后的结果对比如下。

5.5.1 飞行冲突结果分析

对管制单位而言，守住安全红线是最重要的原则。飞行冲突的次数和严重程度是评价空中交通是否安全运行的合适指标。

现行的航路侧向安全间隔标准为10km，当航空器之间侧向间隔小于最小安全间隔标准50%时存在极大安全隐患，可视为重度飞行冲突。本文将侧向间隔小于5km作为重度飞行冲突的统计阈值，航段长度优化前、后的重度飞行冲突情况统计结果如图8所示。

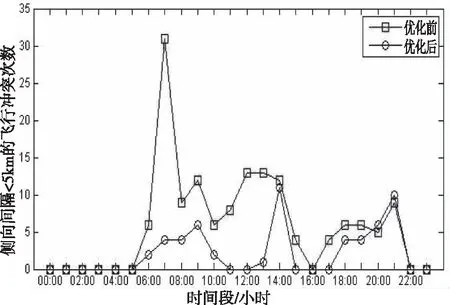
图8 飞行冲突优化效果

图8展示了当航空器之间的侧向间隔小于5km时的飞行冲突次数优化结果对比。仿真结果显示，重度飞行冲突次数总和在优化后减少62.5%，峰值降低87.10%，说明优化后的航路结构能显著减小重度飞行冲突，降低碰撞风险，保证空中交通的安全运行，并提升空中交通流的顺畅度。

5.5.2 管制员工作负荷结果分析

管制工作负荷直接影响到管制员的工作表现，也是空中交通安全问题关注的焦点。本文通过仿真，以管制工作负荷为评价指标证明模型优化的有效性和可行性，验证结果如图9所示。

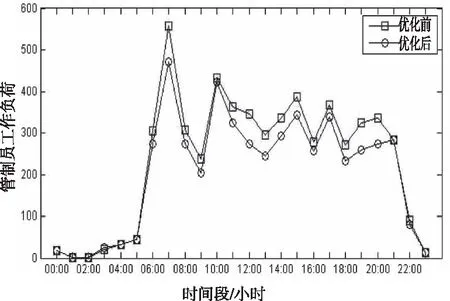
图9 管制员工作负荷优化效果

航段长度优化后使管制员工作负荷总和降低11.78%，峰值降低15.65%，优化效果显著，利于提升空管保障能力，保证空中交通安全、高效的运行。

6 结论

本文基于交通流仿真研究了航段长度优化问题。通过建模、求解和计算，对航段与空中交通流运行安全、效率的影响关系进行了定性及定量分析，研究结果验证了模型的合理性及有效性。得到具体结论如下：

1) 航段长度变化会影响交通流运行参量，一定的范围内，飞行时间和燃油消耗随航段长度的减少呈现非线性增加的趋势；

2)本文建立的模型对优化航段长度组合有显著效果，通过多指标评价，分析了所提模型的有效性和优化性能；

3)航段长度优化后燃油消耗、飞行冲突次数、管制员工作负荷指标优化效果最好。

本文研究了直线航路条件下的航段长度优化问题，下一步将研究更为复杂的多向交叉航路的构型问题。

致谢

感谢中国民航大学空中交通管理学院赵元棣老师对本文提出的宝贵意见；感谢国家自然科学基金(61571441)和国家重点研发计划项目(2016YFB0502405)的资助。