基于相关性的多维时序数据异常溯源方法
王沐贤,丁小欧,王宏志,李建中
哈尔滨工业大学 计算机科学与技术学院,哈尔滨150000
近年来我国制造业持续快速发展。工业互联网的智能工厂已经积累并正在产生大量的工业时序数据。通过对基于采集时间点的多维时间序列数据的分析和挖掘,能够对系统的运行状态进行控制、分析、决策和规划[1],形成了有效的工业知识产生、提取、应用的积极循环,进而实现了对工业大数据的智能分析[2]。
通过分析传感器组传回数据可以检测出工业系统及设备中存在的显性或隐性异常,例如产品质量缺陷、精度缺失、设备故障、加工失效、性能下降、环境突变等[1]。这些故障给企业带来了大量消耗损失。为了降低危害,工业系统和设备会加入一套故障处理方案,由系统运维人员或自动运维程序对数据中显示的异常状态进行判断并介入故障排查[3]。但通过调研发现,在很长一段时间中,工业生产的故障诊断存在着以下一些问题:
(1)工业时序数据具有数据量大、时效性强、模式多样的特点。传统的单维静态数据处理方法存在一定局限性。
(2)利用工业时序数据判别异常类型为系统故障抑或是错误数据存在困难。
(3)工业时序数据可能存在模式相关,这是工业系统的物理属性决定的。但数据可能仅是数学上表现出相关性,可能在整体上并不能表现出相关关系。
为了能够减少工业生产中将数据异常错误归类造成损失,本研究提出了一种基于时序相关环模型的异常来源检测算法。本文的创新点包括:
(1)给出区别于传统单维数据的基于图论的多维时序相关性模型,将相关性分析放在图中进行解释,在不失去严谨性的同时更加直观。
(2)设计了一种在时序相关图中提取最大时序相关环的方法,对异常成因进行溯源。利用序列间的相关关系得到相关序列集合,通过在相关序列中定量分析序列相关性对异常来源进行分类。
(3)在实际的多维工业数据中,通过与基准算法进行比较,本文方法在准确率、召回率以及稳定性上高于基准算法。
1 相关工作
静态数据的异常检测(anomaly detection)研究相对起步较早。现在静态异常检测已经被应用到网络入侵检测、工业探伤、星云探测等多学科多领域,文献[4]识别网络中流量的特定异常分布模式,以确认监控的计算机是否将敏感数据发送给未经授权的其他计算机。文献[5]利用心电图中的正常模式进行匹配,若失配则认为对应患者的心脏存在病变。这是利用已知数据中的特征或固有统计模型挖掘数据中不符合该特征或模型的点或片段检测异常。
利用机器学习的模型进行异常检测已有很多研究,其中基于分类和基于聚类的方法得到了广泛应用。基于多类别分类的异常检测技术假定训练数据包含属于多个正常类别的标记实例[6]。这种异常检测技术可以学习得到一个多维分类器,以区分每个正常分类与其余分类。如果一个测试实例没有被任何分类器归类为正常,则该测试实例被认为是异常的。基于二分类的异常检测技术假定所有训练实例都只有一个类标签。这类方法有使用二分类SVM(support vector machine)判别一个正常模式的边界[7],也有利用Fisher 核做判别式指导分类器划分的方法[8]。基于聚类的异常检测技术有:正常数据实例属于数据中的一个聚类,而异常实例不属于任何聚类。基于上述假设的技术将已知的基于聚类的算法应用于数据集,并将不属于任何聚类的任何数据实例声明为异常[9]。正常数据实例位于其最接近的聚簇质心附近,而异常则离其最接近的聚簇质心很远。基于上述假设的技术包括两个步骤。在第一步中,使用聚类算法对数据进行聚类。在第二步中,对于每个数据实例,将其到其最接近的群集质心的距离计算为其异常分数[10]。注意,如果数据形式中的异常本身是聚簇的,则上述技术将无法检测到此类异常。
近些年数据的时序属性不断受到重视,基于时序数据的异常检测方法也得到了很大发展。在时序异常检测研究中,对于异常的检测对象而言,时序数据异常主要有毛刺异常(glitch)、点异常(abnormality)和区间异常(interval abnormality)三种[11];在时序异常检测方法上以机器学习方法为主,包括基于聚类和基于分类器的算法。基于聚类的方法将正常或异常数据点聚集并尽可能将二者的距离增加[12]。基于分类器的方法利用确定特征方程的系数得到正常和异常数据的分界。文献[13]利用EM(expectation-maximum)算法做正常数据与异常预测数据的多分类器。文献[14]利用隐马尔科夫方法发现偏序序列中各个正常点或正常子序列所具有的特征,从而将异常点或异常子序列检测并标记处理。文献[15]利用速度约束的概念,配合最大似然估计得到正常情形下的数据值,以此检测异常数据并进行修复。在已有的异常检测方法中,基于机器学习的方法往往开销较大;基于统计模型的方法要求待测数据的分布模式已知,应用存在局限;而约束方法在挖掘较长区间的异常模式时受到计算方法的限制不能很好地使用。
2 研究内容介绍
在一个工业系统中,异常(anomaly)一般被定义为数据中不满足常态、约束、规则、给定模型的不寻常数据值或模式[16]。工业时序数据异常的溯源可能有两种:一种是指工业系统丧失其规定性能的状态,称之为故障;一种是指传感器失灵造成正确数据出现偏差,称之为错误数据。二者都可以引发数据异常,但造成的后果完全不同。
2.1 基本定义
本文的问题定义基于已有研究文献[17]。下面给出一些便于理解本文算法的关键基本定义:
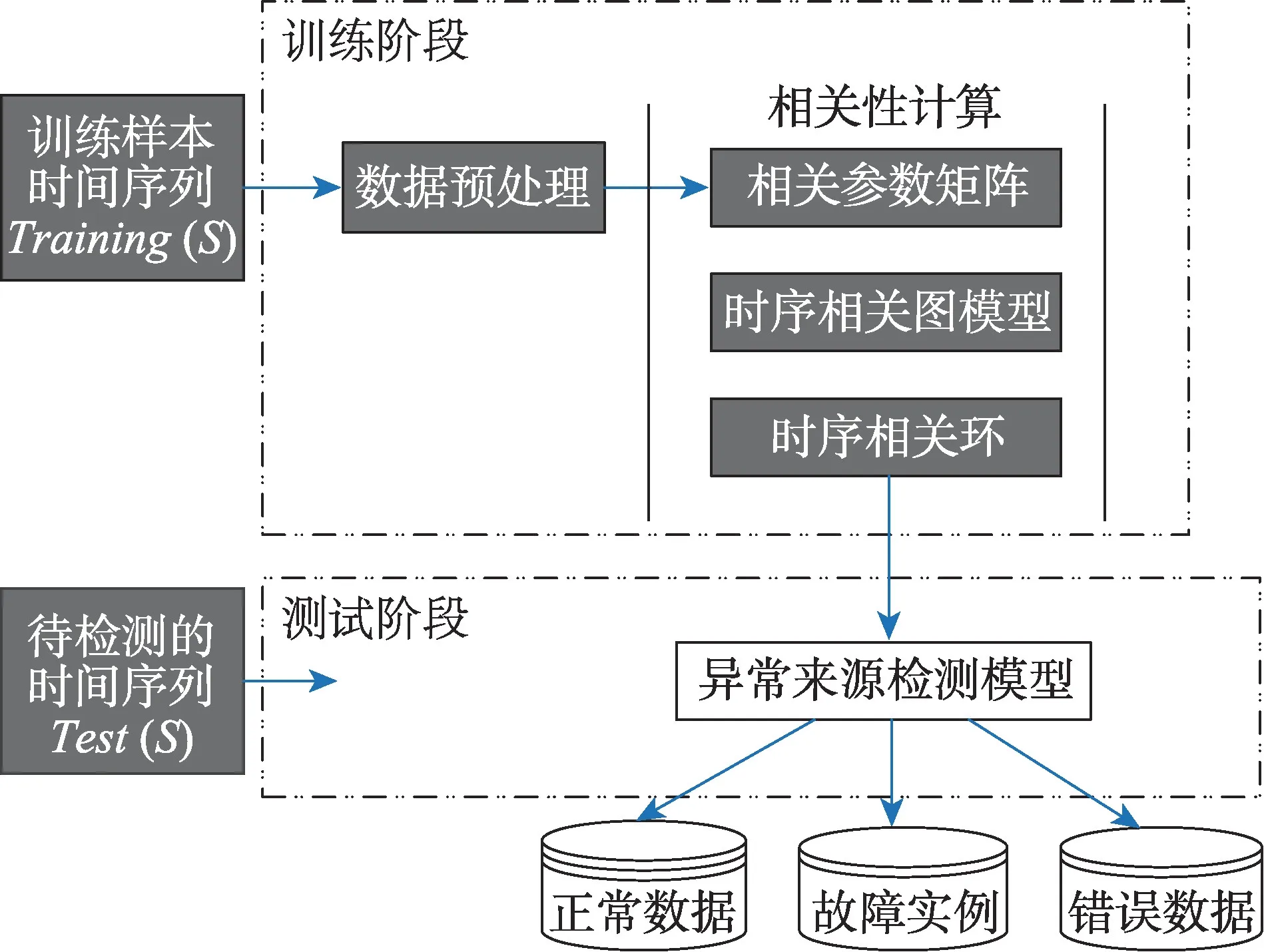
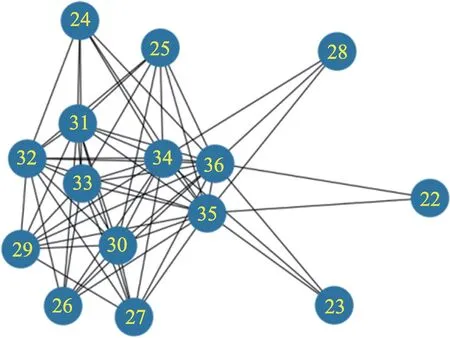
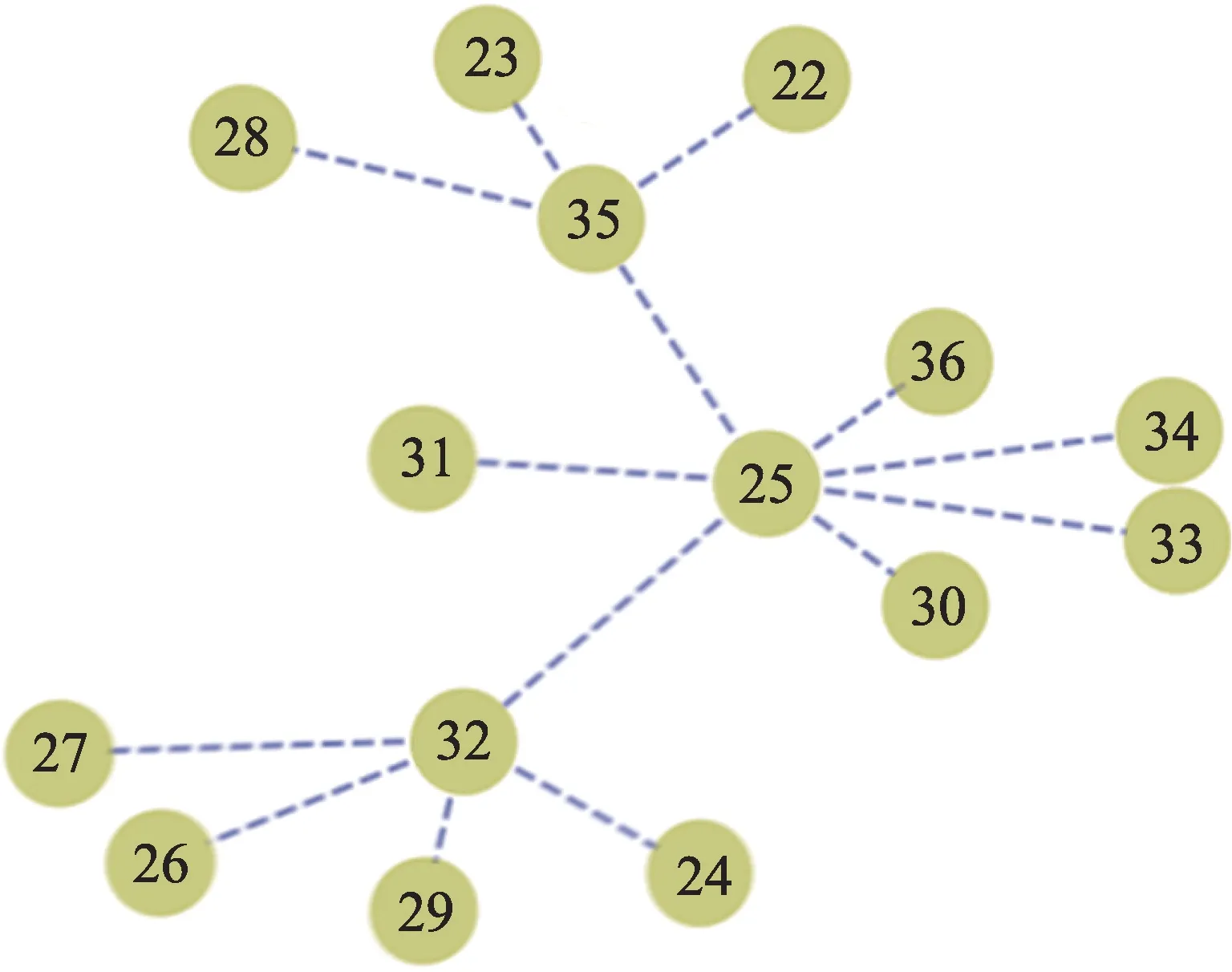
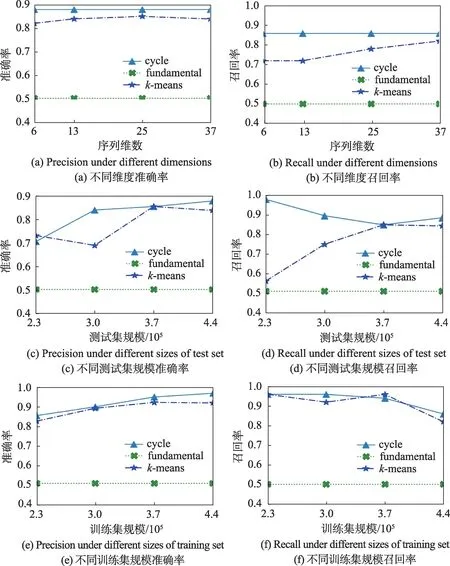
定义1(时间序列)时间序列是由传感器采样的一系列连续的数据点。一条长度为N的时间序列表示为,其中每个序列点表示为一个二元组,xi是一个实数值,ti是时间记录点。对于任意的整数i、j,若i 定义2(多维时间序列)S是一个包含K条具有相同时间点集合T的时间序列集合,记为S={S1,S2,…,SK}。S称为K维时间序列。 定义3(相关系数矩阵)在K维时间序列S的(默认长度为n,下同)时间序列组中,第k个时间序列表示为Sk={sk(1),sk(2),…,sk(n)}。在这个时间序列时间段中,在式(1)中定义相关系数矩阵,用于测量传感器组S上第l时间段内K条序列的相关性,表示为SCM。 定义4(时序相关图)设有图G=(V,E),V={v|v∈SK},E={e|e∈(Rij=1)},则图G被称为时序相关图。 由研究背景所述,现有时序异常检测算法仅能输出发生了异常和异常的表征,无法对异常的来源是故障还是错误数据进行判断。由此,首先对待检测时间序列组的线性相关关系进行挖掘,进而在图论的思想下设计异常检测算法,达到对异常数据的来源进行识别的目的。 本文的时间序列异常来源检测的步骤如图1 所示,主要包含异常相关模型训练阶段(简称为训练阶段)和异常来源判别检测阶段(简称为检测阶段)。 Fig.1 Step of time series anomaly source detection图1 时间序列异常来源检测步骤 训练阶段:该阶段包含两部分,数据预处理和相关性计算。在数据预处理阶段需要对各序列数据的单位和量纲进行标准化。这里规定,训练阶段程序接收并分析的多维时序数据的标签标注都为正确,经调研表明工业生产的绝大多数时间产生的序列数据都是正常运转状态的,正确的工业多维时序数据获取难度不大。 在得到预处理的数据后,将在序列组内计算序列间的相关性关系,得到相关系数矩阵。之后将时序相关关系矩阵表达为一个时序相关图,在图中发掘出所有时序相关环并输出对应的相关序列集,完成对该多维时序数据的训练。 检测阶段:该阶段将对输入的带有异常标签的相同类型序列组通过之前得到的相关序列集分析每个存在异常的序列的异常来源,输出异常的来源类型,以指导工厂对异常情况进行进一步处理。 在工业场景下的多维时间序列数据中,处于同一个系统或具有物理关系的序列间往往呈现出较强的相似性,这里定义序列相关性来定量计算序列之间的相似程度。基于多维序列相关性的异常来源检测方法的整个过程如图1 所示。 得到时序相关关系矩阵后,如果将传感器组的K维序列数据(也就是矩阵中的维度)作为节点,将序列间满足相关关系阈值的关系作为边,可以得到一个时序相关图G。进而利用时序相关图做进一步的分析,把相关关系利用图模型联系起来。 在以每条序列为顶点,每两条相关序列间形成一条边的图G中,构成的连通图可能有一个或多个,这些连通图被称为图G中的连通分量。即在一个工业系统中,时间序列的相关关系可能存在着很多个。由时序相关图的概念,本文提出在时序相关图G的各连通分量中寻找最大时序相关环C。某个时序相关图的其中一个连通分量的样例如图2 所示(图中点标号为对应序列号)。最大时序相关环的定义如下: 定义5(最大时序相关环)在时序相关图G的连通分量(connected component)CC=(V,E),其中在|V|>2 中,若存在一条路径C=(V′,E′),使|V′|≤|V|(|V′|>2),E′={e′|e′∈E且e′首尾相接},且V-V′的点中找不到首尾相接的路径或使已有路径的边增加,则路径C被称为最大时序相关环(maximum time series correlation cycle)。 Fig.2 Connected component of time series correlation graph图2 时序相关图某连通分量 定理1每个时序相关图G的连通分量CC中至多存在一个最大时序相关环。 证明假设CC中存在两个最大时序相关环C1、C2。如果C1、C2 存在重复路径,则C1、C2 可以合并为一个更大的环C,C的顶点集合V=V1 ⋃V2-(V1 ⋂V2),C的边集合E=E1 ⋃E2-(E1 ⋂E2) ;如果C1、C2 没有相交路径,由题设,则C1、C2 分属两个不同的连通分量,与前提在同一连通分量CC中不符合。即CC中不可能存在两个以上的最大时序相关环,得证。 可以看出在一个时序相关图G中可以找到若干个连通分量,在每个连通分量CC中至多存在一个最大时序相关环C,它们包含的顶点总数的大小关系是|V(G)|≥|V({CC})|≥|V({C})|。每个最大时序相关环C表示一组时间序列相关关系。 下面介绍最大时序相关环的搜索算法。由定理1 可知,目标为找到一条在任意连通分量中经过每个点的路径[18]。据此本文提出在每个连通分量CC中搜索一条支撑树T的算法,将连通分量中的边集合CCEdge划分为:所有已知树边加入支撑树边集合TreeEdge以及所有已知非树边加入成环边集合FcEdge,有CCEdge=TreeEdge⋃FcEdge。在生成支撑树的过程中借鉴了最小生成树中的prim 算法,最后得到的T表示成一个支撑树边的集合。图3 即为图2 中时序相关图的连通分量生成的一棵支撑树,这棵支撑树只是其中的一种解,但同一连通分量生成的不同支撑树最后计算出的最大相关环是唯一的。这时引出定理2,描述如何从一个支撑树找到一个环结构。 Fig.3 Support tree of connected component in Fig.2图3 由图2 连通分量生成的支撑树 定理2一条属于FcEdge的边必与对应无向图连通分量的支撑树形成一个环。 证明设fcedge∈FcEdge,则fcedge的两个顶点都在连通分量中,由连通图支撑树的定义可知,fcedge的这两个顶点一定在支撑树的顶点集合中出现。又因为支撑树任意两点间必然存在一条路径,则一定存在一个环,以fcedge的一个顶点为起始点,沿支撑树中的一条路径到达fcedge的另一个顶点,再沿fcedge回到起始点形成一个环。得证。 下一步需要在支撑树中找到一条路径,该路径通过支撑树的任意两个叶节点和根节点。寻找该路径的步骤见算法1。 算法1寻找支撑树中的最长路径 在找到支撑树中可以成环的最长路径后,对于还不属于这个环的其他顶点unfindnode,需要对每个unfindnode进行遍历以确定是否可以将该点加入环以形成一个更大的环,称为环的扩张。定理3 作为最大时序相关环的生成算法中的环扩张算法的一个理论依据。 定理3在支撑树中,若一个顶点不属于现有的环的顶点集合,且该顶点与环的顶点集合中至少两个顶点各自存在一条非树边,则该顶点加入环后可以将环的长度增加。 证明设存在一棵支撑树T以及一个环顶点集合CycleNode,一个不属于CycleNode的顶点v。如果在CycleNode中存在着两个顶点c1、c2,且(v,c1)∈FcEdge,(v,c2)∈FcEdge。又因为存在(c1,c2)∈CycleNode,则v、c1、c2形成了一个三角形。由三角形两边之和大于第三边可知,v加入环后环的长度增加,且环没有断裂,即环的结构是完整的。因此v的加入可以增加环的长度。 接下来用伪代码给出环扩张算法的实现步骤: 算法2环扩张算法 示例说明:由上文中叙述的支撑树可以得到支撑树中由根节点的邻节点作为起始点,对应叶节点生成的路径,如例子可知其中的最长路径为28-34-29-31-24,经过扩张算法后,CycleNode={23,24,25,26,27,28,29,30,31,32,33,34,35,36},为所求的时间序列相关集合CS。 在工业多维时间序列的数据分析中,由于单列异常检测无法很好区分故障和错误数据,本文提出了利用多维时间序列间相关性进行异常检测溯源,算法3 即为基于相关性的异常检测溯源算法。 算法3 多维时序数据异常来源检测 本节对上述算法进行效率分析,上述算法主要的时间和空间开销产生于创建时序相关图和寻找最大时序相关环两个步骤。 3.4.1 创建时序相关图 创建时序相关图时,设计算的时间序列长度为n,序列数量为K。则时序相关图的计算需要计算K维序列中每两列的相关性,在计算的过程中对序列中的每个点有一次遍历,总的时间复杂度为O(n×K2)。 3.4.2 寻找最大时序相关环 设一个K个顶点的时序相关图G中可以划分出N个连通分量CC,在每个连通分量中利用支撑树搜索算法后再使用最大时序相关环搜索算法。算法的快慢与连通分量划分相关,如果每个连通分量的顶点数都接近K/N,则支撑树搜索算法的复杂度约为O(K2/N);如果只有一个连通分量即G的K个顶点构成一个连通分量,则支撑树搜索算法的复杂度约为O(K2)。在每棵支撑树中搜索一个最大相关环的步骤中,在极限条件下即G的K个顶点构成一个连通分量,时间复杂度约为O(K3)。实际工业系统中,一个系统往往K的值较小;而K值较大的系统又往往可以划分成多个内部相关性较强的子系统,因此时间复杂度的规模一般可以接受。 本文的目的是追溯并区分异常序列的异常来源,即该异常属于系统故障还是错误数据。将系统故障作为正例,错误数据作为反例。设每个时间序列组为一个实例单位,实验结果可以分为4 类,分别是: (1)预测正,实际正(true positives,TP); (2)预测正,实际负(false positives,FP); (3)预测负,实际正(false negatives,FN); (4)预测负,实际负(true negatives,TN)。 利用以上4 个分类给出计算公式: 准确率公式: 召回率公式: 实际上计算时还会出现算法判断不存在错误数据的情况,该情况是利用单维时序异常检测算法造成的,在计算准确率和召回率时不加入计算。 本文应用国内某大型火力发电厂的某发电机组数据进行实验。本文在研究了电厂发电机组的某型号引风机连续6 个月的数据后,将其中连续某三个月的历史采样数据作为训练集。该设备共有84 个传感器,分别检测引风机的轴应力、轴温、腔内气体温度、绕组线圈电流及温度等。传感器每8 s 记录一次数据,一共记录了84 列数据。每列时间序列数据经预处理方法去除无效或低质量数据后,最终采用37 列总计74 万个时间点上数据进行实验。 在实验中实现了本文算法。为突出该算法相比其他算法在异常来源检测上的突出表现,本文采用两种算法与该算法做对照: (1)基于约束的异常检测方法。通过检测异常值的波动,检测异常并对故障或错误数据进行分类。 (2)基于聚类的异常检测算法。通过提取时间序列中的特征,区分故障或错误数据。即对潜在相关序列进行聚类,找到聚类中心和搜索半径并确定每条序列所在的分类。 本文分别从测试序列组的序列维数总数、测试集规模和训练集规模方面对上述三种算法检测性能进行了测试,测试结果如下。 4.4.1 序列维数的影响 实验测试了序列维数从6 列提高到37 列的过程中,本文提出的最大相关环算法(cycle)和两种对比算法(单列检测算法fundamental 和k聚类算法kmeans)的准确率和召回率。由图4(a)、图4(b)可以看出,虽然相较之下k-means 算法的准确率在特定条件下表现较好,但本文算法的准确率、召回率以及不同维度下的稳定性都略高于k-means 算法,其中准确率保持在87%左右,较k-means 算法提升约0.09;召回率保持在86%左右,平均较k-means 算法提升0.11 左右。k-means算法的召回率能够随着维度上升有所提高是因为序列维度升高使数据量增加,减少了kmeans 算法陷入局部最优解的可能性。但是因为本文算法较k-means 算法多利用了序列间相关性这一特征,使该算法较k-means 的准确率和召回率都略高,也更加稳定。这里要说明一下,单列检测算法几乎无法判断出异常的来源,因此后续的测试将不再单独介绍该算法的效率。 4.4.2 测试集规模的影响 本小节实验了不同测试集规模对上述算法性能的影响。测试结果如图4(c)、图4(d)所示。从图中可以看出,随着测试集规模的增加,最大相关环算法和k-means 算法的准确率都有所提升,在某些测试集条件下k-means 的准确率可以达到甚至超过本文算法,但稳定性仍存在不足。而最大相关环算法的召回率则稳定优于k-means 算法。测试集规模增大后,本文算法的基于半监督的特性使该方法的准确率仍较优于k-means算法。 Fig.4 Effectiveness analysis in experiment图4 实验有效性分析图 Fig.5 Efficiency analysis in experiment图5 实验效率分析图 4.4.3 训练集规模的影响 不同训练集规模对算法准确率和召回率的影响如图4(e)、图4(f)所示。可见随着训练集规模的提升,本文算法和k-means 算法的准确率都有所上升,且本文算法的准确率一直较k-means 算法高出0.03至0.05。而随着训练集规模的上升,二者的召回率都有所下降。但从两图仍可以看出,在训练集的规模增加或减少时,本文算法的稳定性都优于k-means算法。 4.4.4 算法速率比较 图5(a)~(c)是在上述变量的场景下运行时间的比较。从中可以看出本文算法的运行时间远小于kmeans 算法。虽然本文算法在训练阶段需要一些时间,但利用训练步骤得到的环顶点集合可以使异常来源检测算法在0.1 s 内输出结果。该算法因为不需要在每次检测时对原数据进行额外计算而在流数据处理上较k-means算法有更大优势。 本文研究了基于统计相关性方法的异常检测问题,提出了解决异常来源检测问题的框架结构,利用实际遇到的问题进行示例分析,分别介绍了多维时间序列相关性计算算法和多维时序相关性的最大时序相关环算法以及基于前两种算法的多维时序异常来源检测算法。本文在实验部分说明了该方法的稳定性、运行速度和性能都较传统的朴素基于机器学习的异常检测算法有所提高。
2.2 方法概述
3 多维时序相关性计算方法
3.1 建立时序相关图
3.2 构建时序相关环


3.3 多维时间序列异常来源检测


3.4 算法效率分析
4 实验与结果
4.1 度量标准

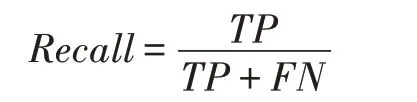
4.2 数据集
4.3 对照算法
4.4 方法有效性分析

5 总结

