复数复杂网络的修正延时投影同步
张 昊
(太原理工大学信息与计算机学院,山西 晋中 030600)
1 引言
近些年来,高维混沌系统,特别是高维复杂网络动力系统,由于其在物理,化学,工程力学领域的潜在应用,吸引了越来越多研究者的兴趣[1-3]。其中一种广泛被接受的研究方法就是用动力系统表示复杂网络中的各个节点,然后通过设计有效的控制器,同步整个网络到固定轨道。如今,人们已经发现许多种同步现象,比如说完全同步[4-6],相同步[7,8],延迟同步[9],投影同步[10],广义同步[11-14]等。而在许多实际情形中,复杂网络的同步往往存在一定时间的延迟,因而对于复杂网络延时同步的研究显得非常重要。近几年来,人们对复杂网络延时同步的研究取得了大量成果,如Zuo等设计了带有时变延迟的复杂网络指数同步框架[15]。Guo等在不假设网络是可约和对称的前提下,用牵制控制的方法研究了复杂网络的延时同步问题[16]。Ji等研究了带延时耦合的动力网络中的延时同步问题[17], Tang等人研究了两个复杂动力网络的混沌延时同步[18], Wang等人研究了多权值复杂网络的广义延时同步[19], Zhang等人采用牵制控制研究了分数阶复杂网络的外部延时同步[20]等。
此外,研究者们在考虑延时的同时,不仅研究了复杂网络的完全同步,还研究了复杂网络的其它同步现象。由于完全同步和反同步可以看做是特殊的投影同步,因而在考虑复杂网络同步问题时,研究者常常将系统的延时与同步的投影结合在一起考虑。Zhang等用脉冲同步的方法研究了一般网络的延迟同步和投影同步[21]。Wu等研究了局部结构不完全相同的网络的投影延时同步问题[22]。Zheng等人研究了神经型时滞神经网络的投影延时同步问题[23]。
稍显不足的是,以上研究均是在实数范围内研究的,而当系统状态变量取值为复数时可用来描述复数电流,磁盘发动机,高能加速器中的粒子束流等的性质。Mahmoud等研究了不同种类的复数混沌系统的行为和同步问题[24-26],作者基于复数系统,研究了复数神经网络系统中的滑膜控制同步问题[27]。然而现有的关于复数同步的研究并没有应用于具有小世界性和无标度性的大规模复杂网络当中。
本文在前人研究的基础上,将复数变量引入复杂网络,研究了大规模复数网络的延迟投影同步问题,值得注意的是,对于投影同步而言,并不是简单的将系统变量放在复数域内进行研究,而是将修正投影的比例因子也取值为复数,这样无论是变量还是参数均具有了复数性质,网络的同步行为更加复杂。
2 网络模型和理论介绍
由N个节点组成的复杂网络模型可描述为
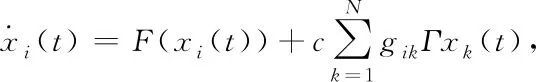
(1)

将F(·)的线性部分和非线性部分分离,可以得到
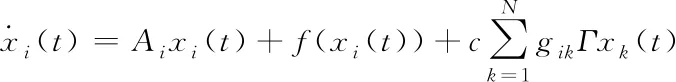
(2)
其中Ai,i=1,2,…,N是线性部分的雅克比矩阵,f(·)为剩余非线性部分,继续分离实部和虚部,得到
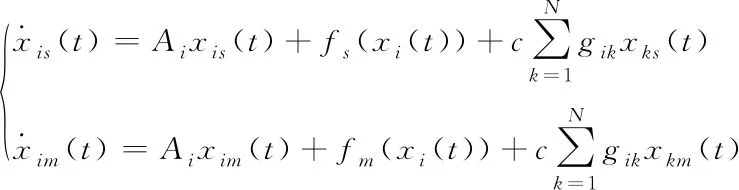
(3)
其中fs表示f的实部,fm表示f的虚部,设参考节点为
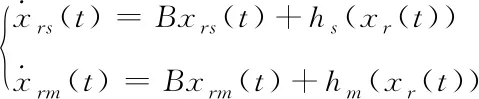
(4)
其中B是参考节点线性部分的雅克比矩阵,hs表示h的实部,hm表示h的虚部。
定义1:
当存在正的时间延迟τ和复数比例因子pu=pus+pumj(pus和pum不同时为零),u=1,2,…,n使得
i=1,2,…,N,u=1,2,…,n,
时,称复杂网络(3)达到了关于参考节点(4)的延时修正复数投影同步,pus和pum分别表示节点内部第u个变量对应投影比例因子的实部和虚部。
引理1[28](Barbalat’s lemma)
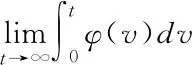
3 延时复数修正投影同步设计
为了使得复数网络与参考系统达到同步,对网络施加外部控制,令控制器为μi=μis+μimj,μis表示μi的实部,μim表示μi的虚部则有
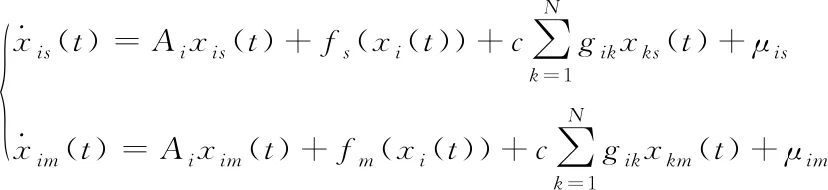
(5)
根据延时修正投影同步的定义,代入复数状态变量和复数投影比例因子,可以得到状态变量关于复数投影的误差为
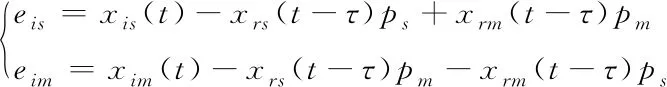
(6)
其中
eis(t)=[ei1s(t),ei2s(t),…,eins(t)]Τ
eim(t)=[ei1m(t),ei2m(t),…,einm(t)]Τ
结合以上误差,由网络(3)和参考系统(4),可得对应网络的同步误差系统为
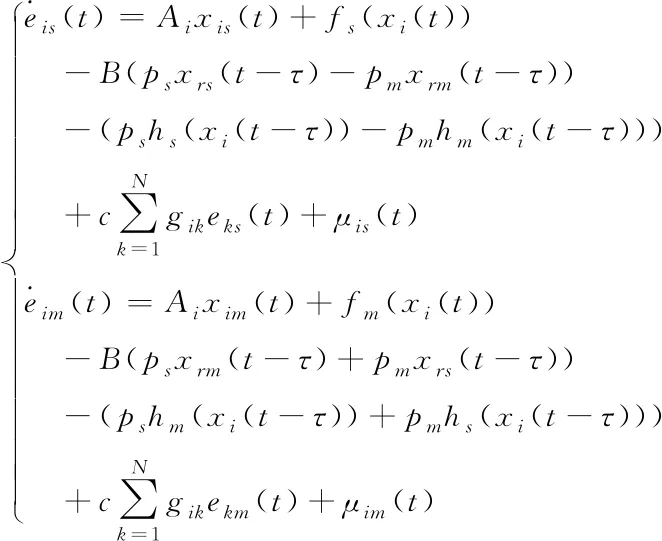
(7)
为了让投影误差(6)趋于零,需要设计相应的控制器使得误差系统(7)稳定,从而可设计同步控制器为
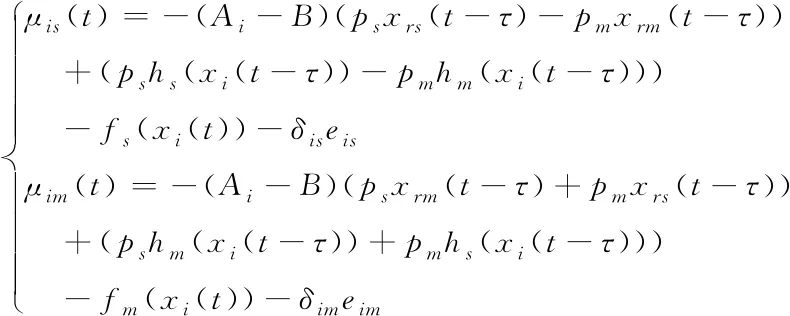
(8)
其中δs>0和δm>0。
当考虑复数系统时,必须将实数部分与虚数部分分开研究,而当研究其稳定性时,可以将实部与虚部统一考虑,则有以下定理成立。
定理1:当
证明:
对于复数系统,可设定复数李雅普诺夫函数如下
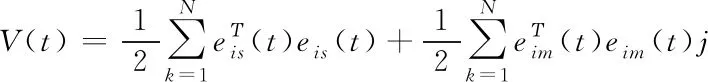
(9)
将控制器代入误差系统,并对该李雅普诺夫函数求导可以得到
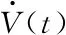
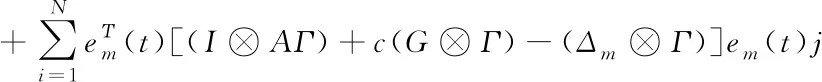
其中
es(t)=(e1s(t),e2s(t),…,eNs(t))Τ
em(t)=(e1m(t),e2m(t),…,eNm(t))Τ
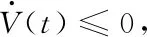
评述:
当对网络中的部分节点采用以上方法进行牵制控制时,可以看做是
Δs=(δ1s,δ2s,…,δps,0,…,0)Τ
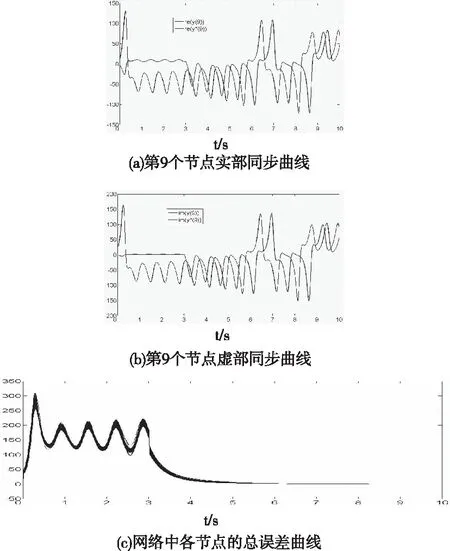
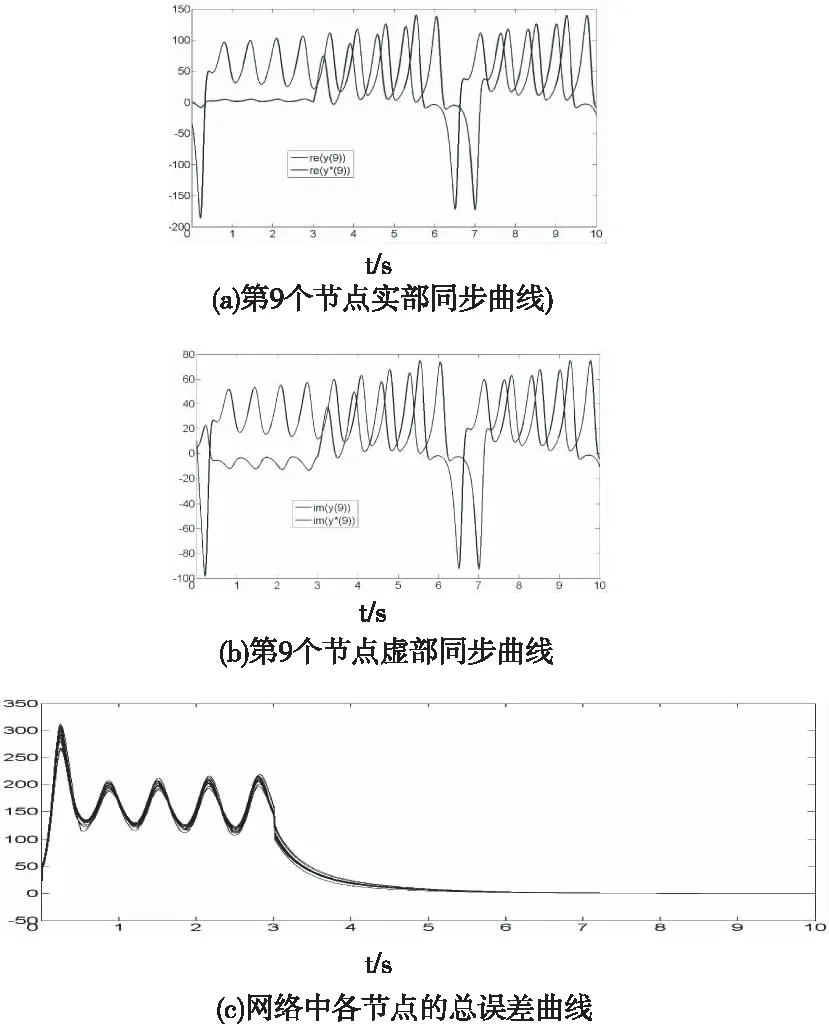
p,q是正的整数且1 推论: 对于特殊的线性矩阵A,如果A是负定的,可以取Δs=(0,0,…,0)Τ,Δm=(0,0,…,0)Τ来使得网络达到同步,即不需要加入线性反馈控制项。 在这一部分中,将针对不同拓扑结构和不同节点数目的网络进行模拟,假设网络中节点都可以用如下复数Lorenz系统来描述其动力学行为 其中conj表示对应项的共轭复数。 NW小世界网络是一种典型的复杂网络模型,采用随机概率 来加边的方法构造网络该复杂网络,与当前节点有连接的邻居节点范围定义为,以下为对应不同规模NW网络对应不同参数时的情况。 首先,选取网络的节点数N=15,随机加边概率为0.6,连接邻居范围为8, 随机生成网络邻接矩阵为: 在本部分,选取网络的节点数N=15,随机加边概率ν=0.6,连接邻居范围K*=8, 随机生成网络邻接矩阵为 为了方便起见,设定如下变量来衡量网络中每个节点的实部和虚部总误差: 令网络耦合强度c=0.03,选取复数投影为p1=2+5j,p2=3+8j,p3=6,延时选取为τ=0.5s在3s时对网络施加控制,选取前10s 进行观察,可以得到仿真结果如图1 所示。 其中re(·)代表实部,im(·)代表虚部。从图1(a)和图1(b)中可以看到对于网络中随机抽取的节点9,其第2个变量的实部和虚部在施加控制后迅速达到了同步,且存在延时,而图1(c)则说明整个网络的实部和虚部都达到了类似于节点9的延时同步。 在实际复杂网络中,网络节点数往往比较多,节点之间的连接并没有4.1.1小节中那样紧密,选取网络的节点数N=100,随机加边概率,连接邻居范围, 随机生成网络的同步图像如图2 所示。 图2 当N=100时,复数NW小世界网络的复数投影同步图像 从图2(a)和图2(b)中可以看到对于网络中随机抽取的节点9,其第2个变量的实部和虚部在施加控制后迅速达到了关于复数投影的延时同步,而图2(c)则说明整个网络的实部和虚部都达到了类似于节点9的同步。 世界杂网络的类型有许多,除了以上典型的NW小世界网络之外,还有BA网络也是另一种典型的复杂网络模型。采用增加节点和随机加边的方法生成网络,选取初始网络的节点数N1=10,最终生成网络的节点数N2=15,对于新生成的每个节点随机加边数为5, 随机生成网络及其同步图像如图3所示。 图3 当N=15时,复数BA网络的复数投影同步图像 从图3(a)和图3(b)中可以看到对于网络中的延时同步情况,图3(c)则说明整个网络都到达了同步。 本文将复数系统引入到了复杂网络中,对于该类状态变量为复数的复杂网络,考虑了网络的延时,以及对于复数系统而言特有的复数投影,提出了复数复杂网络中的复数投影延时同步。延时在许多复杂网络中都存在,而复数投影式复数系统才有的特有同步现象。本文所提方法可以通过改进得到Pinning控制器和自适应控制器,对于合适的线性与非线性划分,甚至可以在不添加线性反馈控制项的基础上使得网络达到同步。最后,对不同拓扑结构,不同规模以不同类型的复杂网络进行了仿真,均能在网络的实部和虚部得到复数投影延时同步,这表明了无论网络是稀疏还是稠密,规模庞大与否都可以达到同步。值得注意的是,这也是首次在变量和投影项都是在复数范围内取值时来考虑复杂网络的投影延时同步问题。仿真结果说明了方法的有效性。4 数值仿真
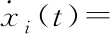
4.1 NW小世界网络模型

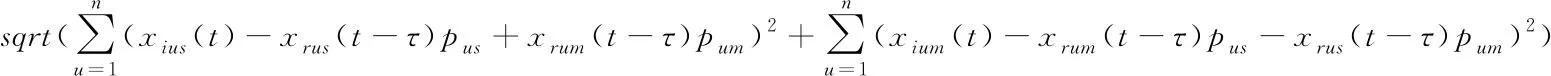
4.2 BA网络中的复数投影延时同步
5 结论

