抗干扰通信网端到端延迟上界仿真分析

闫新娟，刘芳菊，严亚周*

(1. 湖南工学院计算机与信息科学学院，湖南 衡阳 421002；2. 南华大学计算机学院/软件学院，湖南 衡阳 421001)

1 引言

无线网络已经成为互联网的主要组成部分[1-2]，其使用效果和性能分析已经成为互联网技术研究和发展的重点，众多专家学者对此进行了全面而详细的分析。端到端通信是抗干扰通信网络和分布式计算的核心。构造相应的抗干扰通信网络，并将消息从网络中的一个节点发送到另一个节点的问题，受到众多学者的重视，如文献[3]考虑到安全性能因素，提出了一种基于NTRU(Number Theory Research Unit)的端到端轻量级混合密码机制，满足工业控制网络的较少资源消耗和较少时间消耗要求。文献[4]利用深度学习在结构化信息表示和数据提取上的优势，提出一种自编码器端到端物理层优化方案，有效提升收敛速率。然而，由于端到端数据节点的介质不同，严重影响了端到端通信协议的性能。同一网络中消息的传输时间不可能相同，甚至消息的发送和接收顺序也不尽相同。

为了对通信网络端到端的研究进行详细的分析，提出了一种抗干扰通信网络端到端时延上界的仿真方法，更换更加优异的仿真平台，在获取更加有效的分析结果的同时，节约仿真方法的开发时间，降低设计成本。

2 抗干扰通信网端到端延迟上界仿真方法设计

在本次设计中，为了抑制通信网端到端的延迟抖动，原有仿真方法中的不足展开优化，选择仿真工具TrueTime构建高精度网络仿真模型，为后续研究提供可靠性较高的数据，保证文中设计方法的使用效果。较精准地控制本次研究过程，将设计过程设定如图1所示。

图1 抗干扰通信网端到端延迟上界仿真方法设计流程

根据上述设定流程，对本次研究中的方法设计部分展开控制。同时在仿真方法设计完成后，构建相应的实验环节，对此方法的使用效果展开分析。

2.1 构建网络仿真模型

根据本次研究需求，选择仿真工具TrueTime作为此次仿真方法的设计平台。仿真工具TrueTime是 Matlab软件中的工具箱，其具有简化网络控制系统、嵌入式系统与控制器的优点[5]。将此工具应用到仿真方法的设计过程中，需要对通信网络的逻辑层次结构进行设定，具体内容如图2所示。

图2 抗干扰通信网在TrueTime仿真中逻辑层次结构

在图2中，将抗干扰通信网络模型构建为时钟模型、交换机模型以及主机模型3部分，通过对时钟模型的研究，完成抗干扰通信网端到端延迟计算过程。

在本环节中，主要使用时钟模型，完成文中设计方法的设计过程。时钟模型可模拟多个时钟，为了将时钟漂移引入到此模型中，在其中引入漂移因子[6-7]，设定此模型在可配置的时间间隔内保持不变，具体时钟计算公式如下所示

t′=t+β(Δti+Δtj)

(1)

式中，t′表示下一报文的发送时间，t表示当前仿真时间，β表示报文发送过程中调度表的时钟转动次数，Δti表示一个时钟的转动时间，Δtj表示平均时钟漂移。为了获取更加真实的仿真结果，将平均时钟漂移的变化量不计入计算过程中，以此实现仿真周期的高精度计算。除时钟仿真外，在终端系统上实现网络协议，对网络的信息调度表、调度器以及分类模块和同步模块进行分析仿真。将此模型整合为网络模型，对网络中的各个流特征进行设置，具体内容如表1所示。

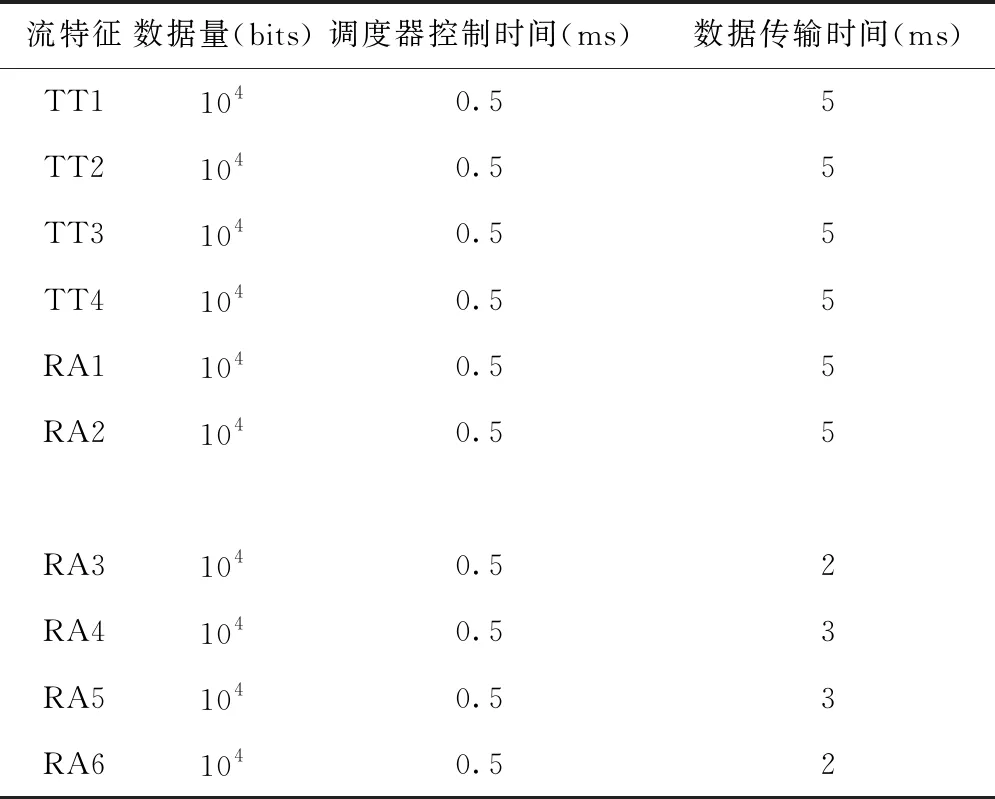
表1 通信无网络仿真模型各个流特性设计结果

表1中，对仿真过程中的信息进行分类，并用调度表对其内容实时处理，同步到接收模块，及时处理消息，实现抗干扰通信网络信息接收与处理过程仿真。

2.2 抗干扰通信网端到端延迟计算

在上述设定网络模型中，进行对应的抗干扰通信网端到端延迟计算。根据TrueTime仿真工具的使用特点，将模型中的时间系统定义为能够在指定时间内完成系统功能的响应系统(约束条件)，同时，使用网络的实时性指标表示报文传输过程中的端到端延时。对于抗干扰通信网络而言，报文的传输主要通过数据链路层的MAC层中的协议实现[8-9]，则在此次研究中，可使用C表示传输中的报文，将其端到端延时过程表示如下：

设定报文发送节点为up-send，则其上层协议处理及排队延时表示为Kup-send(C)，发送节点的MCA层排队延时表示为KMAC-send(C)，报文发送过程中，报送所需物理时间表示为JC，数据传输过程中的网络延时设定为ε。使用recv表示报文接收节点，则此节点报文接收过程中，MCA层排队延时表示为KMAC-recv(C)，接收节点的协议处理以及排队延时表示为Kup-recv(C)。使用以上设计内容，将报文传输过程中的端到端延时Kjtj(C)的计算内容表示如下

Kjtj(C)=Kup-send(C)+KMAC-send(C)

+JC+ε+KMAC-recv(C)+Kup-recv(C)

(2)

式中，数据传输过程中的网络延时ε可使用对应公式得到准确的数值，具体公式如下所示

ε=d/v

(3)

式中，d表示发送节点与接收节点之间的最大距离，v表示网络中的数据传输速度。与此同时，发送过程中所需物理时间JC也可使用功能计算，具体内容如下

JC=S(C)/E

(4)

式中，S(C)表示报文的帧长度。将网络参数带入此公式中可得到估算值。在通信网络运行过程中，协议的处理主要通过计算机处理器完成。因此，协议的处理延时具有不确定性，Kup-recv(C)仅能得到估算值。但根据式(2)，可得到端到端延时变化规律，具体如图3所示。

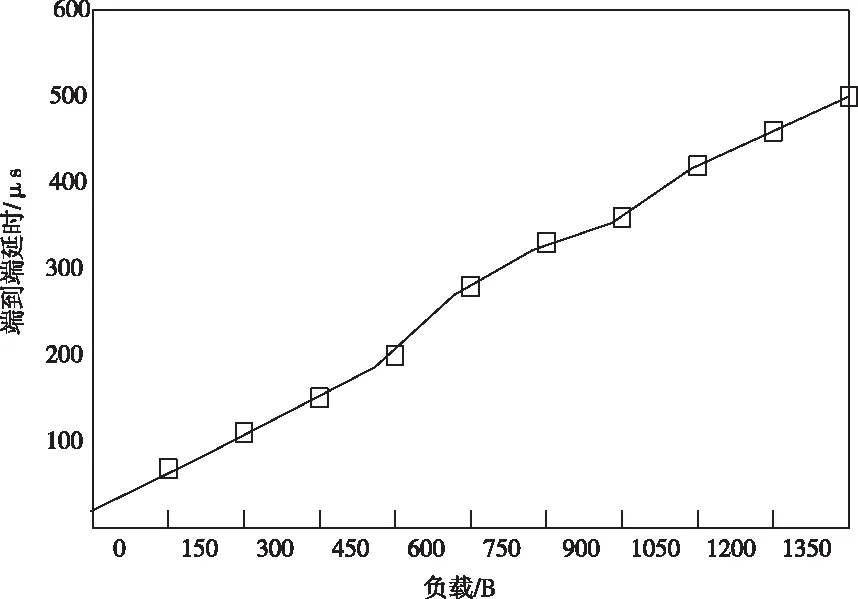
图3 抗干扰端到端延时变化规律

通过图3可知，在报文量增加的过程中，延时会随之增加，因此在本次研究中的通信网端到端延迟上界应符合此变化规律。

2.3 通信网端到端延迟上界演算

在本次研究中，将主要对通信网端到端延迟确定上界以及通信网端到端延迟抖动上界进行研究。将通信网络的报文发送过程设定为数据分类器[10-12]，则其总延时表示为

W=ΔW+w

(5)

式中，ΔW表示端到端延时抖动，w表示固定延时。通过文献研究结果，将端到端延时抖动中的通信网表示为

(6)

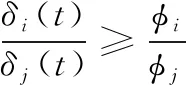
(7)

式中，δ表示网络运行状态，φ表示通信网络中的业务流。在本次研究中，将第i个报文作为研究对象，则其延时的约束条件表示为

ΔWi≤inf{w≥0：δi(t)≤δi(t+d)}

(8)

对于上述公式，将此报文发送过程整合为分流的形式，同时将式(5)、式(6)、式(7)联立，则有：

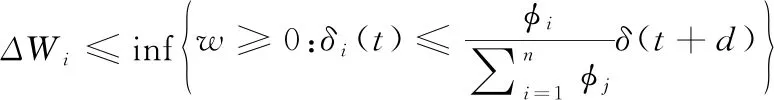
(9)

(10)

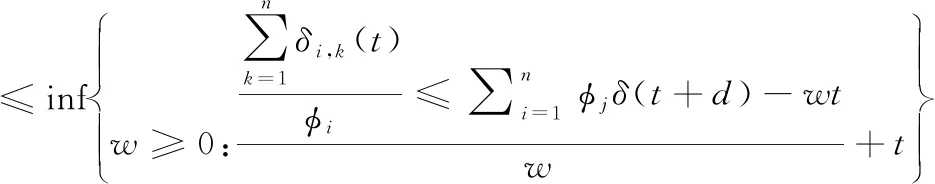
(11)

由此得到延时抖动的上界，则有

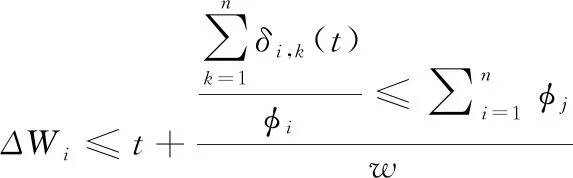
(12)

将此公式与固定延时相结合，则得到端到端延时上界，具体公式如下所示

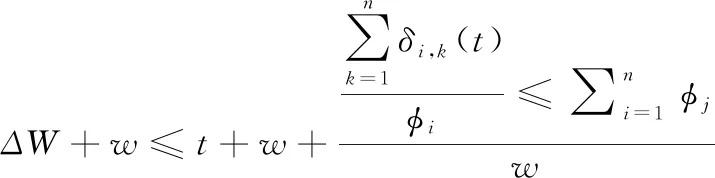
(13)

通过上述计算部分，得到通信网端到端延迟上界。

至此，抗干扰通信网端到端延迟上界仿真方法设计完成。

3 实验论证分析

3.1 实验环境构建

为验证文中提出的抗干扰通信网端到端延迟上界仿真方法的使用效果，在本环节中构建相应的实验环节，对比文中设计方法与传统方法在实际问题应用过程中的差异，其中，传统方法1为文献[3]方法，传统方法2为文献[4]方法。

为了使实验结果更具有可靠性，在Quandl( https：//www.quandl.com/ )中选取某雷达通信系统，以其近3个月的通信数据为实验数据，构建相应的网络模型。在实验模型设计中，将通信模型设定为星型树模式，具体如图4所示。

图4 实验网络模型

图4中，通过箭头表示数据流传输方向。使用此图像对实验对象进行控制，并完成文中设计方法与传统方法对比过程。

3.2 实验方案

在本次实验中，将实验对比指标设定为3组。此3组实验指标的选取均着眼于不同的测试方向，对文中设计方法与传统方法进行全方位的对比。

根据目前对于抗干扰通信网的使用需求，选择数据传输丢包率、通信网模型开销以及通信网模型构建与数据传输仿真耗时比重，共3个实验指标。在实验的过程中，为提升实验结果的准确性，将实验周期设定为多轮实验的形式，将得到实验数据的均值作为最终的实验结果，体现多种实验方法的使用效果。

3.3 数据传输丢包率实验结果分析

由图5可知，文中设计方法在模拟通信网络数据传输过程中丢包率较低。同时，数据模拟量增加的前提下，文中设计方法的丢包率长期处于同一数值下且波动较小。与文中设计方法相比较，传统方法在此指标对比过程中，数据传输效果显得较为薄弱。随着实验中的数据模拟量不断增加，传统方法1与传统方法2 的数据丢包率不断增加且丢包率波动较大。

图5 数据传输丢包率实验结果

3.4 通信网模型构建开销实验结果分析

为了使此指标更加具象化，将通信网模型构建开销设定为模拟主机的CPU占用率。由图6可以看出，在此指标对比过程中，文中设计方法的通信网模型构建开销对于传统方法而言相对较低。在文中设计方法的使用过程中，当仿真数据量达到30%时，运行过程中的模拟主机CPU占用率逐渐趋于平稳。传统方法1与传统方法2 运用过程中产生的模拟主机CPU占用率与数据模拟量呈正比关系，如数据量不断增加，容易造成模拟主机运行异常的问题，严重限制了通信网范围，因而可以判定文中设计方法的使用效果优于传统方法。

图6 通信网模型构建开销实验结果

3.5 通信网模型构建与数据传输仿真耗时比重实验结果分析

由图7可知，文中设计方法的通信网模型构建与数据传输仿真耗时比重较为稳定，且比重较为合理，在两项仿真处理工作中，耗费时间较为合理，同时可得到较好的仿真效果。传统方法1与传统方法2的信网模型构建与数据传输仿真耗时比重在不同的数据量下，具有不同的运行时间。且通过对图像的系统分析可知，此两种方法的信网模型构建与数据传输仿真耗时比重不佳，如使用此方法造成仿真结果精准度较差的问题。由此可知，文中设计方法的使用效果优于传统方法。

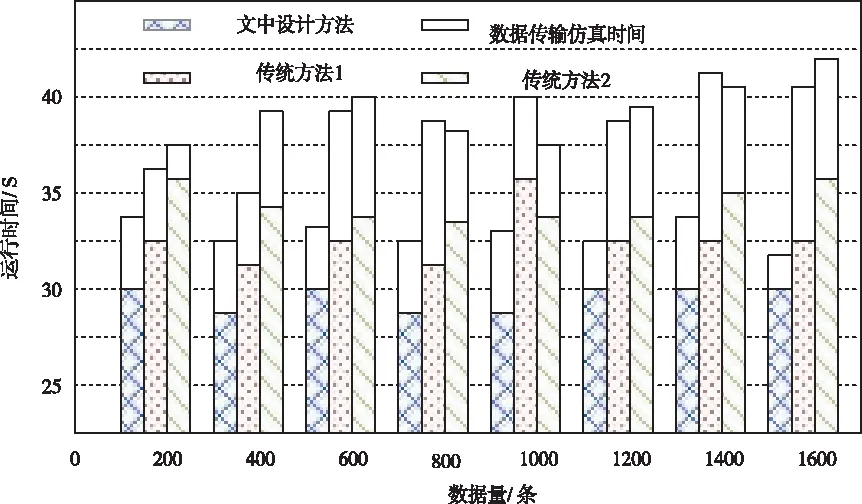
图7 通信网模型构建与数据传输仿真耗时比重实验结果

在此次研究中通过数据传输丢包率实验结果、通信网模型构建开销实验结果以及通信网模型构建与数据传输仿真耗时比重实验结果，对文中设计方法与原有方法进行了系统的分析，由实验分析结果可知，文中设计方法的使用效果优于传统方法。

4 结束语

1)数据传输丢包率实验结果长期在2%左右波动下且波动较小。

2)将通信网模型构建开销设定为模拟主机的CPU占用率，分析通信网模型构建开销，仿真数据量达到30%时，运行过程中的模拟主机CPU占用率逐渐趋于平稳。

3)通信网模型构建与数据传输仿真耗时比重较为稳定，且比重较为合理，在日后的研究中可使用此方法对抗干扰通信网展开研究。