冗余惯性导航系统信息一致性判断方法
赵欣艺 高晓颖 踪 华 李 冰 李宇明
1.北京航天自动控制研究所,北京 100854 2.宇航智能控制技术国家级重点实验室,北京 100854
0 引言
由于运载火箭、飞机、舰船等运动体的可靠性要求越来越高,任务越来越复杂,需要导航系统在运载火箭任务中,在提供可靠、高精度导航信息的同时具备成本低、重量轻、功耗低的优点。
冗余设计是提高导航系统可靠性的技术途径之一。以运载火箭为例,目前国内运载火箭CZ-3A系列、CZ-2C采用双七表冗余激光惯组,CZ-5、CZ-7运载火箭采用2套六表激光惯组和1套六表光纤惯组的方案。常采用主从模式和投票模式进行传感器信息的判断[1]。欧洲阿里安火箭采用了双冗余设计,Space X的猎鹰火箭采用分布式冗余惯组设计[2]。一般冗余设计的判别准则是少数服从多数的阈值判别方法。即预先设置阈值,在一定时间区间对测量同一参数的多个传感器输出结果进行比较,当差值大于设定阈值时,根据少数服从多数的原则进行取舍,最终结果可以采用取平均值或者中间值的方式决定[3-4]。这种方法可以实时给出冗余系统的传感器输出结果,但由于阈值是事先通过经验设置的,一般要求测量同一物理量的传感器精度一致,才可以通过阈值判断。而随着运载火箭等对体积、重量、功耗等的要求越来越高,三个同样高精度惯组的冗余模式,势必会存在体积重量大,成本高的影响。因此传统冗余方案一般只用在大型运载火箭中,小型商业运载火箭一般只采用一套高性能的惯组。
MEMS作为一种微型惯组器件,虽然精度不如光学惯组高,但在体积重量和成本上有很大优势,可以考虑作为冗余惯组设计的一部分,然而由于与激光光纤惯组等高精度惯组的精度不同,两种惯组进行冗余设计时,不能简单地采用阈值设置通过少数服从多数的方式进行判断。
在多传感器一致性数据融合的研究中,LUO R C提出置信距离测度,作为衡量传感器一致性的判断依据[5]。之后,很多学者对该方法进行改进和优化[6-7]。但是没有改变的是,基于置信距离测度的一致性判断过程中依然需要设置阈值,且对传感器性能的先验知识要求严格,要求传感器的测量结果符合正态分布,且方差已知。因此在应用中有诸多不便,针对惯组测量量短时间内变化快的特点,实际工程应用中并没有采用这种判断模式。
而在冗余惯性器件故障隔离的研究中,奇偶向量检测法研究比较多,文献[8]针对冗余三捷联惯组提出最优奇偶向量法,该方法与设置阈值法相比有一定优势,但最优奇偶向量法针对的是噪声特性一致的惯性器件,对于本文所提出的精度差异较大的冗余惯组设计并不适用。
文献[9]针对精度差异悬殊的平台、捷联式惯组的主从冗余模式,提出冗余故障诊断及决策方法。但两惯组系统不进行信息互判,只是通过各种门限的设置判别常见故障,一方面,阈值选择依靠经验,另一方面,没有充分利用测量信息。
相对于传统方法,人工神经网络在图像处理,语音识别等方面均表现出了优势。因此,针对以上问题,本文以冗余惯性导航系统为研究对象,利用神经网络,实现冗余惯性导航系统信息的一致性判断,提高导航系统的可靠性。该方法可应用于不同精度导航信息一致性的判断,同时避免了依靠人工经验选择阈值带来的不便。
1 神经网络的构建
1.1 Siamese网络
Siamese网络即孪生神经网络[10]。与普通神经网络的区别在于,孪生网络有两个成对的输入,两个同样的共享权值的网络结构,且没有目标输出。其样本标签不作为目标输出直接用于网络权值调整。最初提出该算法是为了解决签名的识别问题,现在多用于各种图像匹配[11-12],目标追踪[13]等图像处理领域。文献[14]也将其应用在矿物质光谱识别分类上。
本文采用的Siamese网络结构如图1所示。成对信息输入后,经过神经网络的处理,提取出低维度的特征向量,通过计算特征向量的“距离”,作为输入信息对的相似性度量。即网络训练的目的是使得具有一致性的样本对提取的特征向量的距离尽可能小,不一致性的则尽可能大。从而对样本对的一致性实现判断。

图1 Siamese网络结构图
图中,Gw(x)为网络映射函数,x1和x2分别为由2个惯组系统某段时间内的输出构成的数据信息,在Siamese网络中作为输入参数,Ew为特征向量之间的距离。Siamese网络的训练样本是成对存在的,一致的样本对标签设为0,不一致的样本对标签设为1。
1.2 网络结构选择
Siamese网络只是一种网络框架,具体的神经网络设计根据要解决的问题采用合适的结构设计。
为有效利用惯组一段时间内的数据趋势,设计卷积神经网络,该网络由三层卷积层和三层全连接层组成,参数见表1。
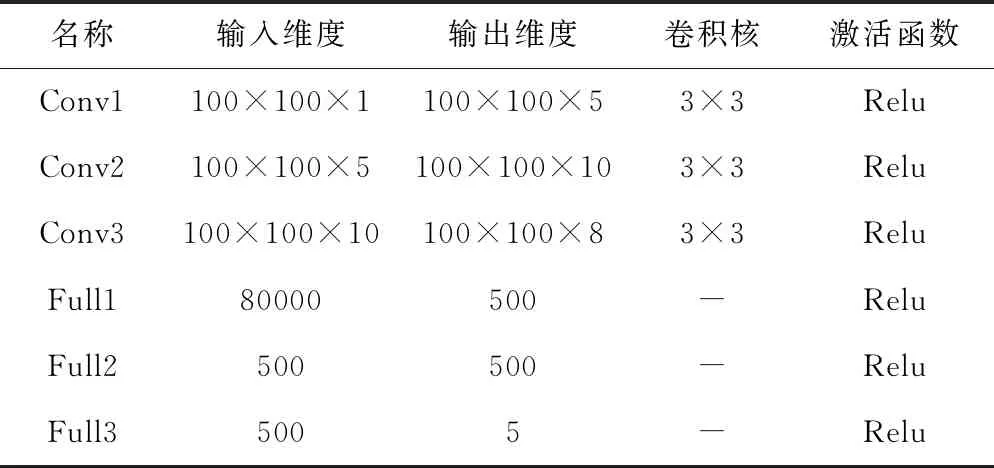
表1 神经网络参数设计
1.3 损失函数设计
神经网络的训练中,需要定义损失函数,由于孪生神经网络的训练样本中,标签不作为目标输出,因此,传统用于分类的网络常采用的交叉熵函数不再适用。损失函数的形式为:
L(w)=(1-Y)LG(Ew(x1,x2))+YLI(Ew(x1,x2))
(1)
其中,LG只计算一致输入的损失函数,LI计算不一致输入损失函数。在最小化损失函数的过程中,理论上,将LG设计为有效区域内的增函数,LI设计为有效区域内的减函数,可以使得训练过程中逐渐扩大一致与不一致样本对提取的特征向量的差距。
本文采用的损失函数如式(2)所示。式中,m为设置的边界,当不一致样本对的特征向量的距离大于m时,该样本对不对损失函数产生影响。特征向量的距离计算采用欧氏距离计算,其公式如式(3)。

(2)
Ew(x1,x2)=‖Gw(x1)-Gw(x2)‖
(3)
2 训练样本的构建方法
本文以高低精度惯组冗余模式的导航系统作为信息一致性研究对象,验证本文方法在不同精度的惯组冗余设计中的有效性。采用模拟飞行的惯组脉冲数据作为训练样本生成的基础,通过建立惯组测量模型,模拟惯组输出。
2.1 惯组测量模型
模拟轨迹的理论脉冲值对应载体系下的真实角增量、视速度增量的值。如式(4)。
(4)
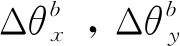
陀螺测量模型为:
(5)

(6)

加速度计测量模型与陀螺类似,不再赘述。
在惯组测量模型中加入不同的误差即设置不同的零次项系数模拟高低精度惯组数据。为更贴近真实情况,两惯组所涉及的模型参数均考虑了与安装等客观因素的相关影响。
2.2 训练样本的构成
Siamese网络多用于图像处理方面的分类问题,采用Siamese网络实现惯组数据的一致性识别问题。沿用图像数据的格式,将待分类数据构造成n×n的矩阵形式,本文采用100×100的矩阵。将六表(3个陀螺,3个加速度计)的惯组作为一个惯组系统,在系统级层面对数据一致性进行判断。
加速度计和陀螺的综合测量结果,解算后会通过飞行器的速度、位置和姿态角反映出来,当其中一个惯组系统测量出错时,两惯组系统解算出的速度、位置和姿态角的变化趋势会出现差别。样本生成中,除考虑测量脉冲数据直接转化的物理量之外,也考虑结合解算后的速度、位置和姿态数据。
训练样本由导航系速度、位置、姿态角,体坐标系角增量、角增量累积量、视速度增量、视速度增量的累积量共7类数据组成。每类数据包括3个方向上的数值,共21维。
利用一段时间内惯组测量数据的变化趋势提取特征用于识别。因此采用一段时间内的导航数据进行样本构造。惯组解算更新时间为0.02s,两惯组采用同初值进行惯导解算。解算4000次(80s),等时间间隔取出100组数据,分别得到两个100×21的矩阵,矩阵构造示意图如图2所示。由于网络设计的输入是100×100,因此将其余部分补零。即产生一组样本对。步长设置为2000,再次统一初值并进行解算得到下一组样本对,以此类推。

图2 输入数据矩阵示意图
由测量模型加不同误差生成的测量值得到的样本对为一致性样本对,标签设置为0。
模拟不一致样本对生成时,主要模拟惯性器件经常出现的故障模式,即极性相反、常零值和常峰值3种情况,标签设置为1。
为测试网络训练结果的泛化能力,即能否适应未出现过的故障模式,能够从相似度方向上解决一致性判别问题,训练样本和测试样本分开生成,且加入不同的故障模式,例如,在不一致样本生成的过程中,训练样本中加入正向峰值,测试样本中加入负向峰值。
3 仿真试验
导航系统一致性判断网络模型基于Pytorch平台,使用Python语言实现。训练样本如2.2节所述构建。
3.1 仿真参数设定
惯组测量模型1误差参数:
激光陀螺零偏误差:0.05(°)/h;石英加速度计零偏误差:0.0001m/s2。
惯组测量模型2误差参数:
MEMS加速度计零偏误差:0.01m/s2;MEMS陀螺零偏误差:5(°)/h。
安装误差设置一致。随机产生,为10-4rad量级。
惯组数据更新周期为0.02s;全时长为1542s。
训练样本数据:552对,其中,包含一致样本对316对,不一致样本对236对。
测试样本数据:497对,其中,包含一致样本对275对,不一致样本对222对。
3.2 阈值选择
由于Siamese网络最终实现增大一致样本对之间和不一致样本对之间提取出的特征向量的距离的差别。因此,最终判断时需要设计阈值,该阈值由网络训练得出。
阈值选择:(1)综合准确度较高;(2)不一致样本对漏检率为0。
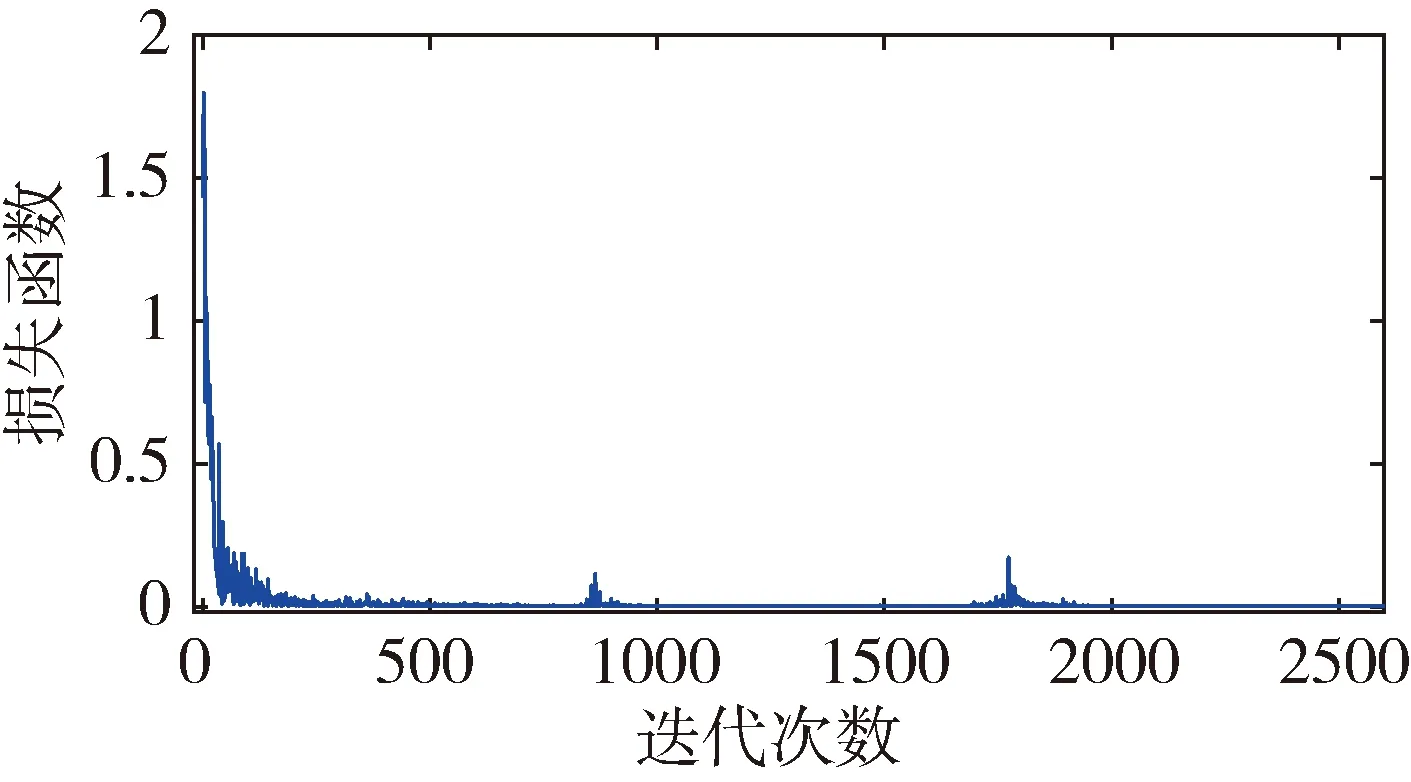
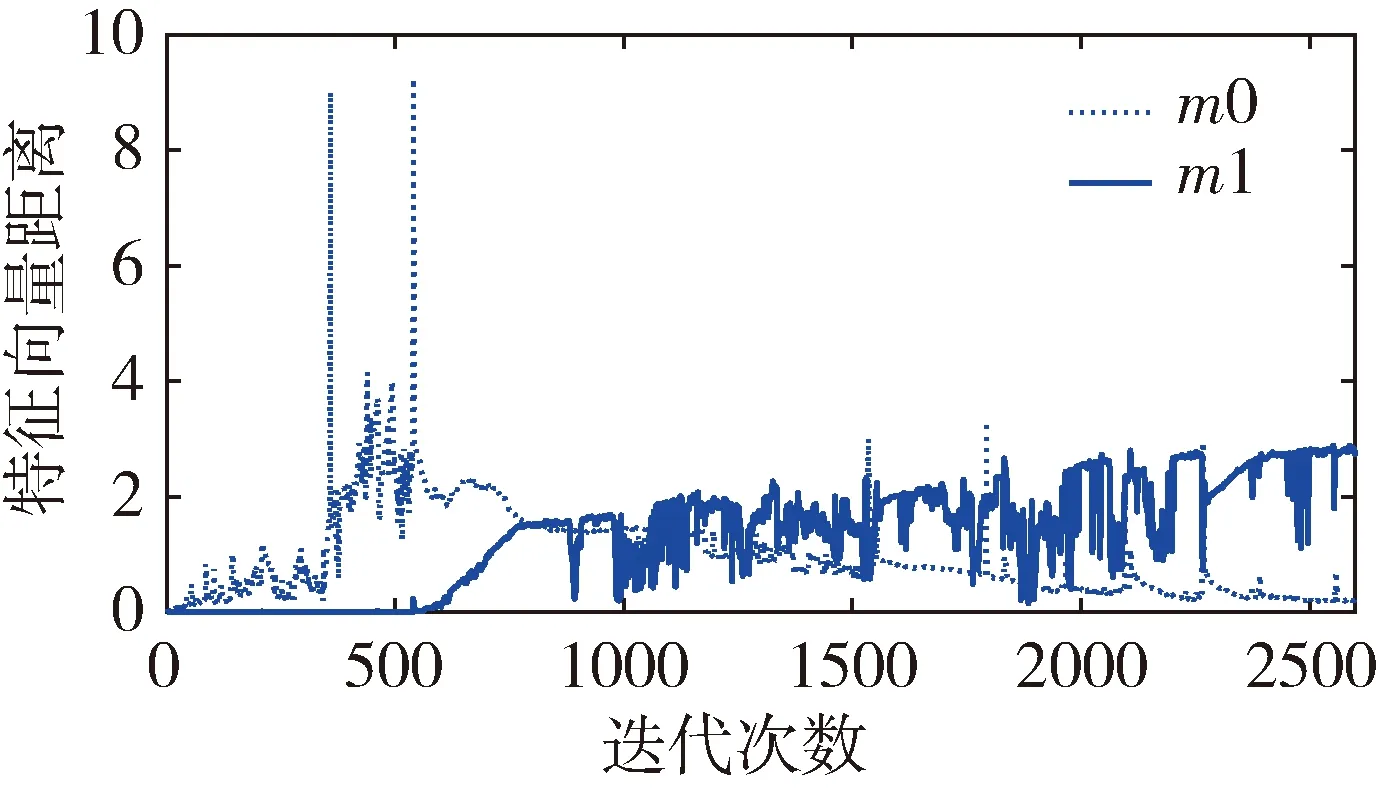
定义所有一致样本对特征向量距离的最大值为m0,所有不一致样本对特征距离的最小值为m1。训练过程中有如图3和图4两种情况。数轴上小于m0以及大于m1的两区域分别表示样本中所有一致样本对和不一致样本对经过神经网络提取的特性向量的距离范围。以m1作为阈值,可满足不一致样本对漏检率为0。当训练结果可以满足m0 图3 样本对特征距离示意图1 图4 样本对特征距离示意图2 因此阈值分别选择a1=0.5(m1+m0),a2=m1。 网络优化方式采用Adam方式,学习速率设为0.0005。训练结束条件:(1)训练样本迭代中连续300次满足m0 训练过程中,损失函数的值随迭代次数的变化率如图5所示,可以看出,损失函数的值稳步减小并在最后趋近于0。 图5 损失函数随迭代次数的变化情况 为更直观地表现训练效果,图6是m1和m0随网络迭代次数的变化情况。 图6 m1和m0随迭代次数的变化情况 由图6可以看出,训练过程中,m1和m0的值随迭代次数向m0 训练样本和测试样本随网络迭代次数的准确度如图7~10。 图7 采用a1为阈值时训练集样本随迭代次数的变化情况 图8 采用a2为阈值时训练集样本随迭代次数的变化情况 图9 采用a1为阈值时测试集样本随迭代次数的变化情况 图10 采用a2为阈值时测试集样本随迭代次数的变化情况 由图7~8 可以看出,训练后期网络对训练集的判断准确率达到100%。 由图9~10可以看出,基于训练集训练后的网络可以很好地应用到测试集上。虽然准确度不如训练集稳定,但经过1000次迭代以后的网络,已经可以满足在测试集上大于98.19%的准确率。 本文测试集与训练集样本是分开生成的,针对不一致样本对,部分区别测试加入的故障模式与训练集的故障模式。在加入峰值故障时,训练集加入的是正向峰值,测试集加入的是负向峰值。对应测试样本对约占总测试样本对的1/3,但网络在测试样本上的实验识别准确率依然可以达到98.19%,说明网络具有一定的泛化能力。本文的训练样本只有552对,属于小样本。仿真证明,该方法具有一定的小样本需求优势。 本文采用Siamese网络架构进行了基于学习的冗余惯性导航系统信息一致性分析研究,以冗余的不同精度的惯性导航系统为研究对象,验证了该方法在冗余惯性导航系统信息一致性判断中的有效性。代替了一般冗余惯性导航系统设计中,仅考虑当前值,以设置阈值的方式判断信息一致性的方法。为惯性导航冗余设计不再局限于同精度惯组冗余的模式提供支持。用神经网络模拟人脑判断数据一致性的方式,神经网络训练结果稳定,准确度超过98.19%。为冗余惯性导航信息的一致性判断提供了新思路。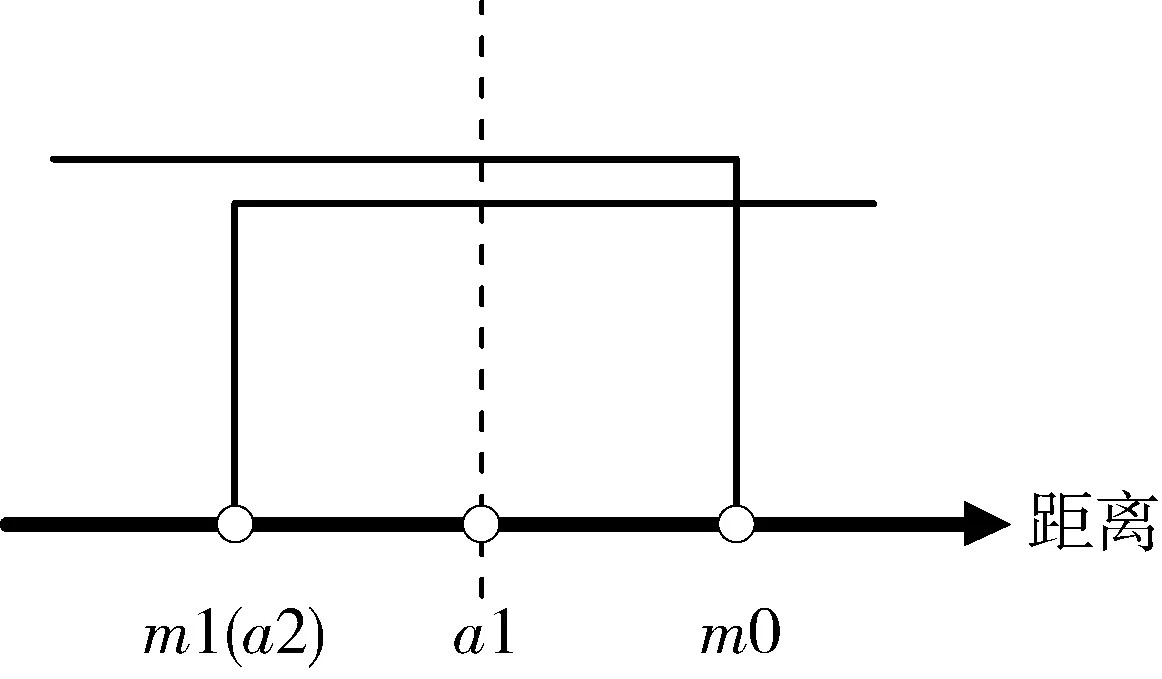

3.3 仿真结果




4 结论

