基于半监督极限学习机的控制力矩陀螺新奇性故障检测*
刘鹭航 张 强 王 虹 郭宝柱 张激扬 王志鹏
1. 中国航天系统科学与工程研究院,北京 100037 2. 北京控制工程研究所,北京 100094 3. 北京交通大学轨道交通控制与安全国家重点实验室,北京 100044
0 引言
随着航天技术的发展,航天器的结构和功能要求日益复杂,作为直接关系到航天器轨控、遥测、有效载荷、能源等系统安全运行的关键系统,航天器姿态控制系统是航天器的重要分系统,任务繁重,系统复杂[1],是航天器正常工作的重要保证,控制系统的微小故障可能导致航天器性能恶化,因此,对航天器姿态控制系统进行状态监控和故障诊断非常必要[2]。控制力矩陀螺(Control Moment Gyroscope, CMG)[3]是航天器在太空调整姿态的执行部件,通过监测控制力矩陀螺运行情况,可以评估航天器姿态控制系统的健康程度,进而保证航天器的安全运行。传统评估控制力矩陀螺的方法是构建寿命与可靠性评估模型,该方法通过分析控制力矩陀螺的退化机理,构建控制力矩陀螺的可靠性模型,从而判断其健康状态。文献[4]通过分析某型控制力矩陀螺的故障模式,使用威布尔分布模型对控制力矩陀螺展开寿命与可靠性评估。文献[5]使用有限元分析和结构可靠性分析进行控制力矩陀螺有限元建模及动力学分析。
然而,可靠性分析方法不能实现控制力矩陀螺运行状态的实时监测,不能保证对故障的实时识别。随着近年来技术的不断进步,控制力矩陀螺的主要失效模式已经由单一部件突发失效引发的整体失效,转变为由于某些部件疲劳、磨损等性能退化而引起的系统性能下降或失效,亟需使用新的方法对其进行检测和评估。控制力矩陀螺的实时监测是保证航天器高精度、高可靠性和长寿命的关键。陀螺通过高速旋转的轮子获得角动量,并通过改变角动量的方向对外输出力矩。监测控制力矩陀螺的转子运行情况,可以实现控制力矩陀螺的实时故障诊断和状态评估。文献[6]使用变转速情况下的霍尔故障检测和信号重构方法对控制力矩陀螺高速转子进行故障检测和重构。文献[7]使用主成分分析算法(Principal Component Analysis,PCA)、基于t分布的随机邻域嵌入算法(t-distribution random neighborhood embedding)和 K均值算法(K- means algorithm)诊断控制力矩陀螺高速转子的故障。文献[8]使用模糊Q学习算法对控制力矩陀螺转子进行故障检测。但是,基于机器学习的算法存在参数调整步骤多、时间长,结果过拟合、局部最优解等问题,同时对硬件要求高,不适应于故障的实时检测。极限学习机是一种人工神经网络模型,该算法不需要人为设置大量的参数,也不需要多次调整参数,计算速度快[9],适用于控制力矩陀螺故障的实时监测。
上述故障诊断模型在训练数据充足且已知训练数据类型的前提下能够准确诊断出控制力矩陀螺转子的故障。然而,控制力矩陀螺在多数情况下都是正常运行,极少出现故障,因此产生的运行数据多为正常数据,缺乏故障数据;使用数量不平衡或者标签不明的正常/异常数据训练诊断模型,控制力矩陀螺故障的识别结果会受到严重影响,因此,新奇检测受到了学术界的广泛关注。新奇检测是基于半监督学习的算法[10],该算法对不同于已知类型数据的数据十分敏感,使用已知的正常数据进行训练,然后对未加标签的数据进行判断,识别出“新出现”的未知故障数据[11]。因此本文提出基于半监督极限学习机的控制力矩陀螺转子新奇性故障检测,该算法将流形正则化与极限学习机进行结合,使得极限学习机能够在数据标签不足的情况下进行半监督学习,使用半监督极限学习机对控制力矩陀螺的正常数据进行训练,然后使用该模型诊断控制力矩陀螺中的新奇故障。此外,本算法使用振动加速度数据进行新奇性故障诊断,原始信号存在模态混叠,不利于故障信息的提取,需要对信号进行时频域分析,并提取出相关特征。算法使用变分模态分解[12](Variational Mode Decomposition, VMD)解决信号模态混叠问题,并将振动信号分解成不同的谐波信号,再使用奇异值分解(Singular Value Decomposition, SVD)提取分解后振动信号的特征,并将该特征作为半监督极限学习机网络的输入数据,对控制力矩陀螺进行新奇性故障检测。本文使用某型控制力矩陀螺转子的真实振动加速度数据,验证结果表明算法能够准确识别控制力矩陀螺的未知新奇故障。
1 方法
1.1 变分模态分解
变分模态分解是一种自适应、完全非递归的模态变分和信号处理的方法,可以将信号分解成不同的固有模态函数(Intrinsic Mode Functions IMF),其中心频率和带宽都是有带宽限制的,通过迭代搜索变分模型的最优解来确定。约束公式为:
(1)
式中:μk表示第k个模态分量,ωk表示第k个模态分量的中心频率,在分解过程中,通过引入二次惩罚因子α和拉格朗日乘子λ,可将最优解问题转换为最小化问题,约束变分问题转变为非约束变分问题,拉格朗日表达式为:
L({μk}{ωk},λ)=
(2)
式中:α可以降低高斯噪声的干扰。
每个模态分量μk在满足ω≥0条件下,由下式迭代生成:
(3)
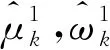
各模态的中心频率ωk由下式迭代生成:
(4)
迭代过程中生成最优拉格朗日乘子:
(5)
满足下列条件,迭代循环结束:
(6)
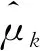
1.2 奇异值分解
SVD使用线性代数运算提取出原始数据的特征值,在VMD将信号分解成若干个IMF后,能够从IMF中提取出特征矩阵,矩阵提取可用下式表示:
X=UωVT
(7)
式中,X表示由原始数据形成维度为m×n的矩阵。U(m×n)和V(m×n)是2个正交矩阵,(ωij≠0,i=jandω11≥ω22≥…≥0)表示奇异对角矩阵,ω11,ω22,…,ωmm是原始数据的奇异值,U被称为左奇异矩阵,V被称为右奇异矩阵。U和V各行之间均正交,且都是基向量。为了获得更多原始数据矩阵的内在信息,选取了奇异值向量(ω11,ω22,…,ωmm)作为特征矩阵的分解结果。
1.3 半监督极限学习机新奇性检测
1.3.1 半监督极限学习机
极限学习机ELM是一种有监督的算法,ELM的算法本质是将训练数据X和Y分别作为输入和输出,训练出X和Y的最佳映射,算法包括了随机学习和输出权值计算。
算法首先要确定隐含层神经元的个数,随机生成输入层和隐含层之间的连接权重和偏置系数,确定隐含层激活函数,使用下式计算输出:
f(x)=∑βG(axi+b)
(8)
式中:xi和f(x)表示输入、输出数据,a和b表示输入层和隐含层之间的连接权重和偏置系数,β表示隐含层和输出层之间的连接权重,G(·)函数表示激活函数。
通过损失函数计算实际输出和预计输出之间的误差,通过最小化误差函数计算隐含层和输出层的连接权值,求解最优化问题min‖f(x)-Y‖2,得到最终的参数(隐含层与输出层之间的连接权重)β*,最后的输出如下所示:
f(x)=∑βG(axi+b)
(9)
由于在实际情况下存在大量无标签数据,在训练过程中需要用有标签和无标签数据共同训练,需要ELM表现出更好的泛化能力,且ELM求解最优化问题是一个线性回归问题,处理标签数据缺失的问题时,需要使用正则化参数和基于有标签样本和无标签样本相似度的拉普拉斯矩阵,结合岭回归方法处理最优化问题,令,f(x)=Gβ则最优化问题如下所示:
(10)
f(x)=Gβ=[F1,F2,…,Fi]
(11)
式中:C为基于训练误差的正则化系数,用于权衡训练误差和模型复杂度,防止过拟合;L为拉普拉斯矩阵,由无标签和有标签样本共同组成,能够衡量样本之间的相似度,通过岭回归求解最优化问题,可知最优化解为:
β*=GT(E(l+ul)+CGGT+LGGT)-1CY′
(12)
1.3.2 新奇性检测
新奇性检测能够识别与已知的种类不同的数据种类,使用已经训练后的无监督极限学习机,能够识别有差异的数据种类。首先,输入与训练数据标签相同的数据,使用min‖f(x)-Y‖2计算输出差异值,相同标签数据的差异值最大值作为判别的阈值,然后输入需要判断的数据,计算输出差异值,与阈值进行比较,即可判断输入数据的标签是否是新奇故障。
2 实验分析
本实验使用某型号控制力矩陀螺的轴承振动加速度数据,轴承规格为B7004C,组件主要部件为上、下2个轴承,轴承具体的参数如表1所示,测试实物如图1所示,采集到的正常数据信号如图2所示:
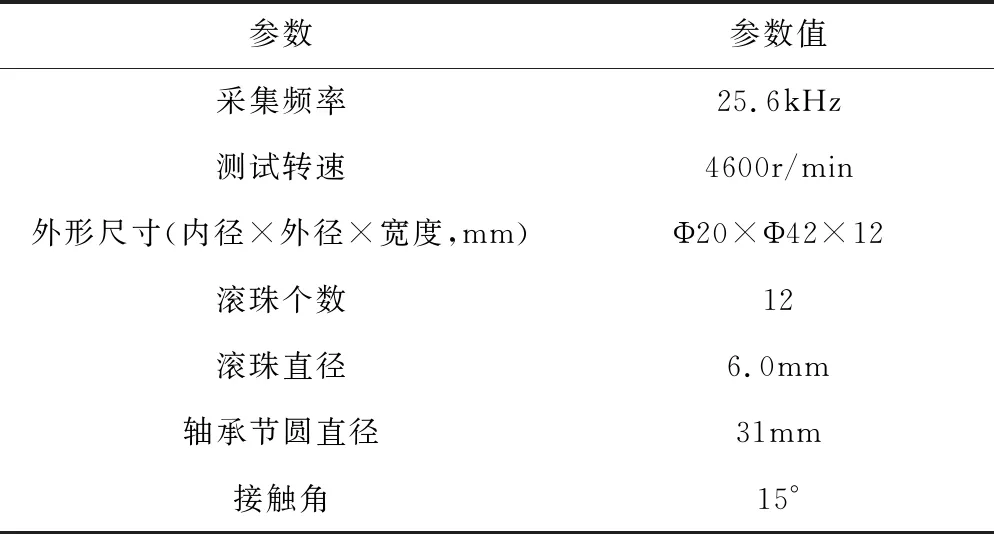
表1 轴承参数

图1 振动测试实物
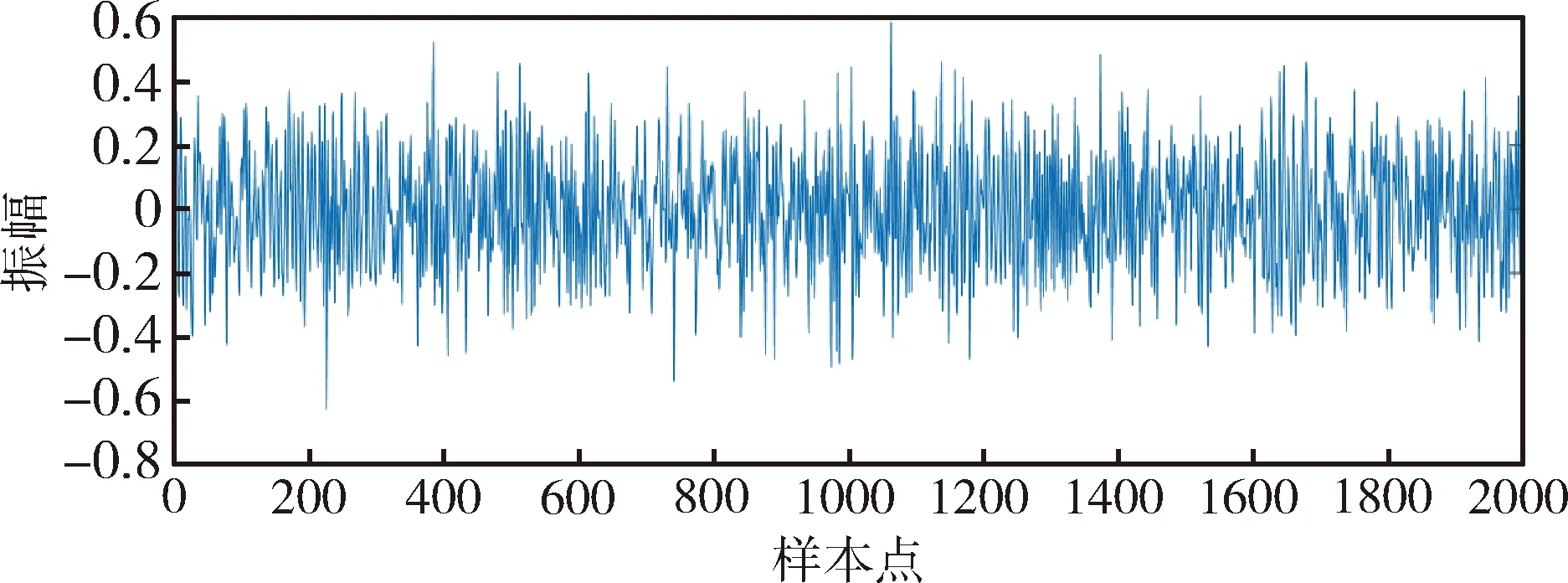
图2 轴承振动信号
利用VMD对原始信号进行分解,需要给出预设的IMF个数和惩罚因子α的值。α的值为2560, IMF个数为8。在信号分解后,SVD从IMF中提取奇异值特征,形成特征值矩阵,图3为VMD分解后的信号图,表2为提取后的特征值:
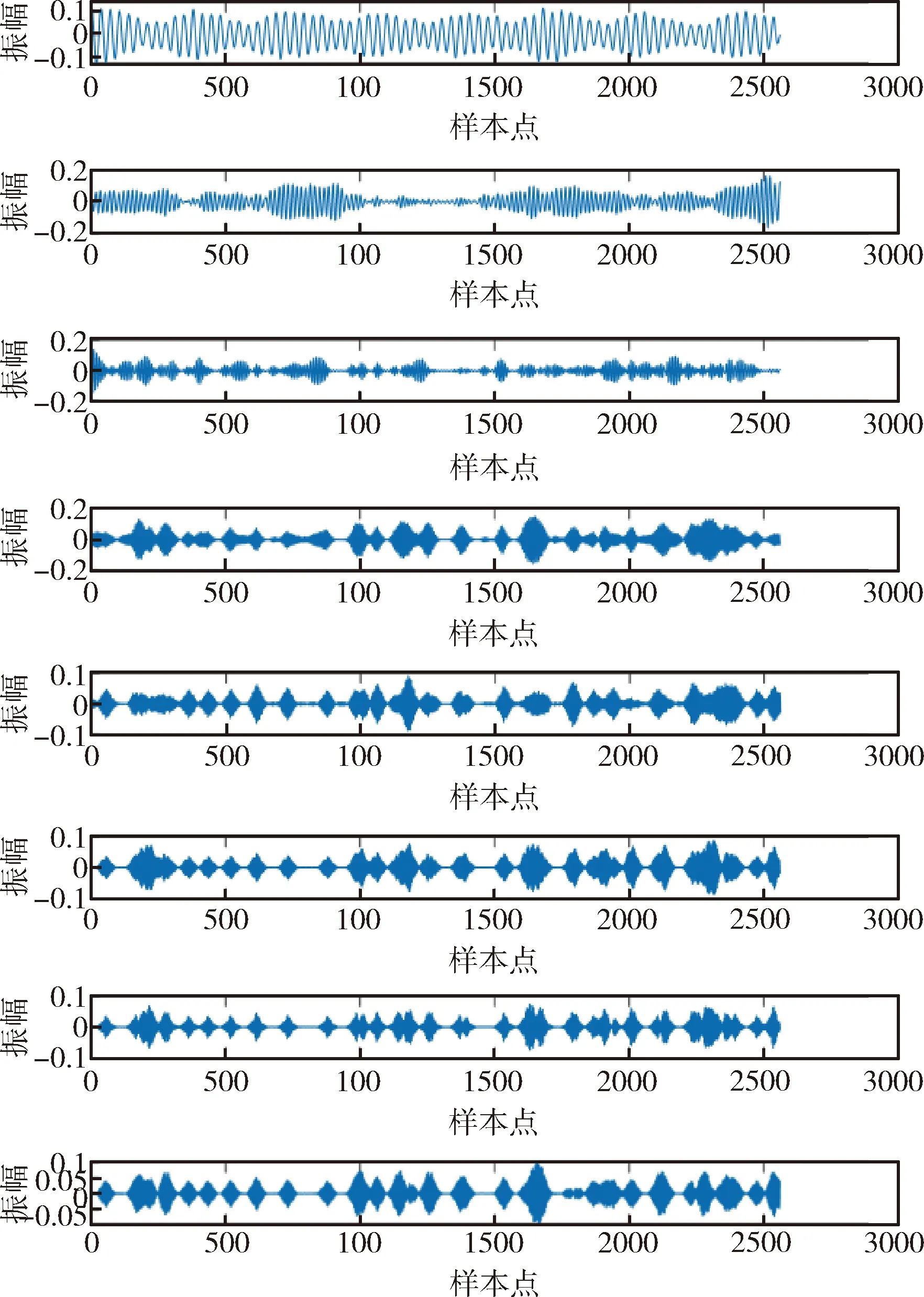
图3 IMF信号

表2 正常信号特征值
使用SVD提取信号的特征后,将一部分正常数据作为有标签样本,其他正常数据与故障数据作为无标签样本进行训练,有标签样本数据分为3部分:1)作为新奇型检测的输入,同时与无标签的正常数据和异常数据生成基于数据相似度的拉普拉斯矩阵,这样既能保证作为新奇型检测单一类型数据的要求,又能在缺少大量数据标签的情况下,能够诊断出轻微故障;2)作为测试输入,得到训练后的半监督极限学习机的测试结果,与预期输出进行对比,通过设置不同隐含层节点等参数对网络进行重新调整;3)用来计算正常数据之间的误差,该误差作为区别正常与异常数据的阈值,能够对无标签数据进行新奇性故障诊断。
使用不同隐含层节点数的半监督极限学习机对有标签数据进行训练,挑选出使训练数据计算误差最小的网络模型,不同的隐含层节点数对应的计算误差值和训练时间如图4和5所示:

图4 不同隐含层节点个数的训练误差值
如图4所示,当隐含层节点增加以后,模型的训练误差值不断减小并趋向于稳定,但如图5所示,训练时间随着隐含节点个数的增加而增加,因此考虑训练时间和训练误差,隐含层节点数确定为1100,通过训练得到训练样本的差异值取值范围,从而确定正常数据的阈值,则阈值为3.0219×10-5。
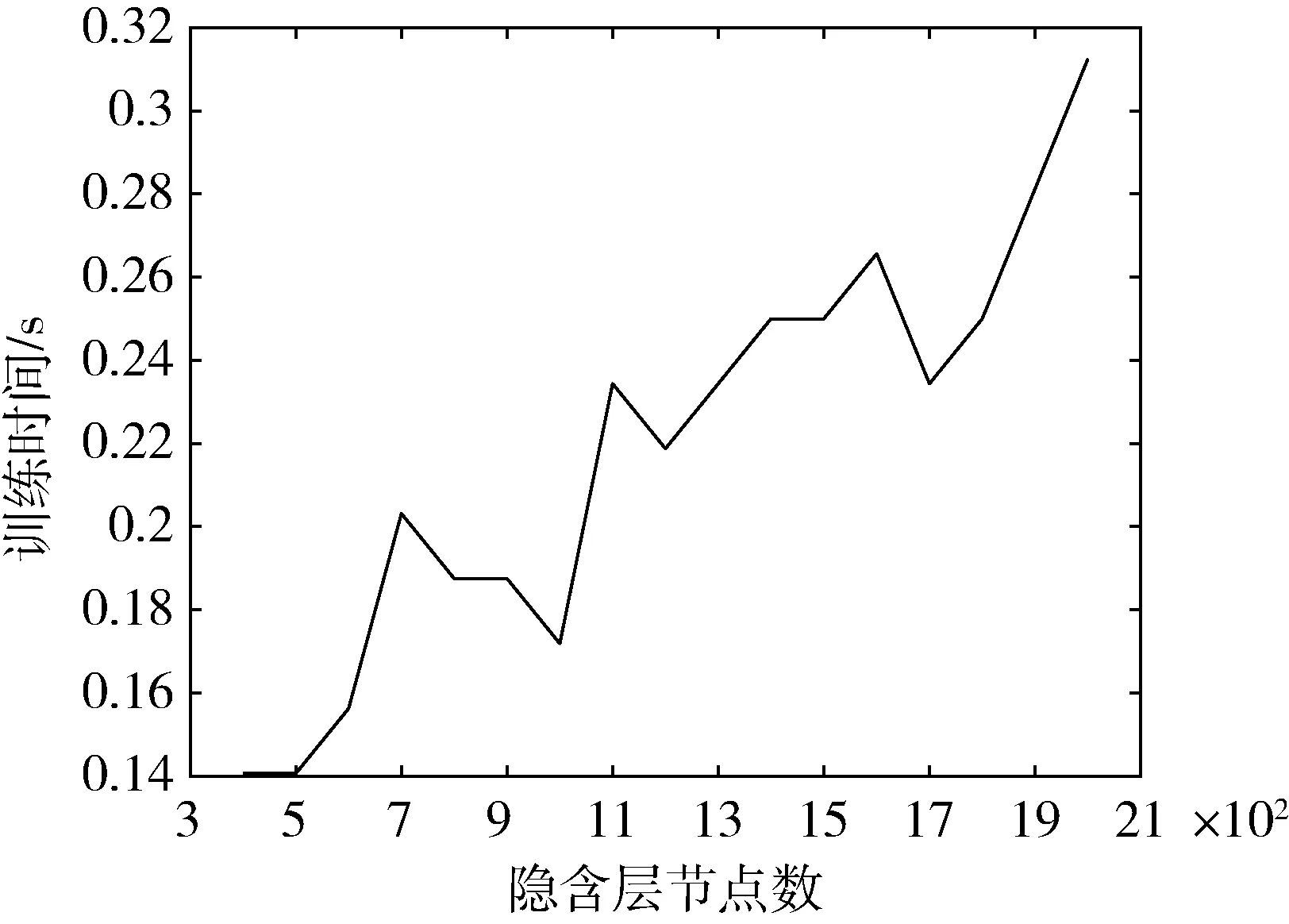
图5 不同隐含层节点个数的训练时间
输入无标签数据,计算差异值,并进行新奇性故障检测分类,正常数据的差异值如图6所示,故障数据的差异值如图7所示。
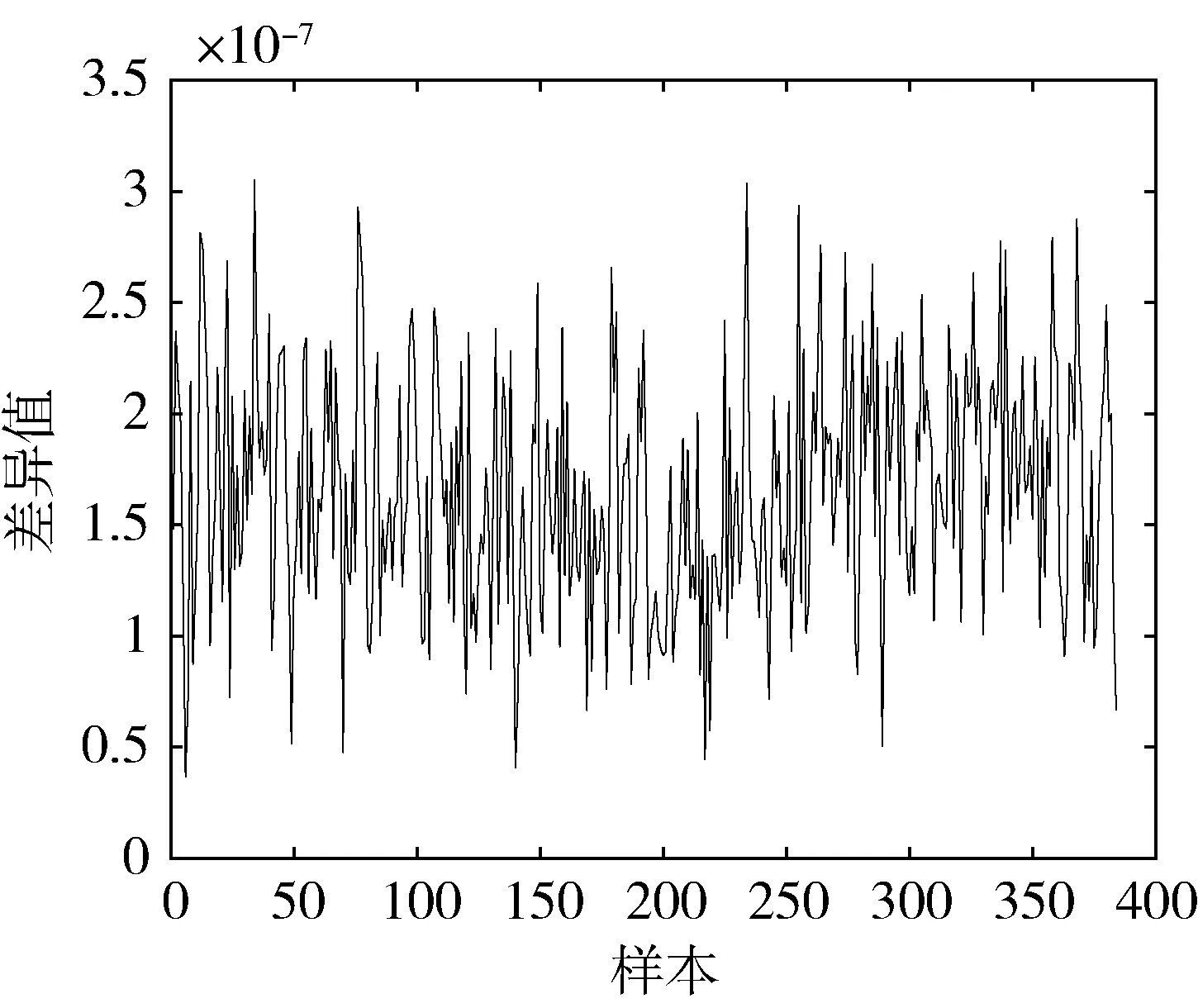
图6 无标签数据(正常数据)的差异值
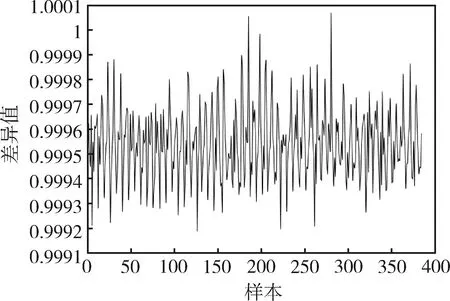
图7 无标签数据(异常数据)的差异值
由图6~7可得,根据无标签数据的差异值判断新奇性故障,故障数据的差异值都在0.99以上,大于阈值3.0219×10-5,而正常数据的差异值在3.6784×10-8~ 3.0499×10-7,远远小于阈值,因此,基于半监督极限学习机能够准确识别出所有的故障数据。
3 结论
本文提出的基于半监督极限学习机的新奇性故障检测算法,能够在控制力矩陀螺转子数据类型缺失的情况下进行故障检测,该算法结合变分模态分解和奇异值分解算法处理控制力矩陀螺转子的振动加速度数据,实验结果表明该算法准确识别了类型未知的故障数据,可以实现对控制力矩陀螺转子运行状态的实时监测,保证了航天器的在轨安全飞行。

