INS辅助的动态北斗双频周跳探测与修复方法*
郭泽辉 庞春雷 张 闯 张 良
空军工程大学信息与导航学院,西安 710077
0 引言
北斗(BDS)卫星导航信号容易受到电磁干扰或障碍物遮蔽,导致接收机短暂失锁,载波相位观测值出现整周跳变,而且周跳具有继承性[1],会影响后续历元的载波相位观测值,降低定位精度。特别是当接收机处于动态环境时,运动状态会影响载波相位测量值的连续性,增加周跳探测的难度。因此,有必要针对动态情况下的周跳探测与修复问题进行研究。
经典的周跳探测方法包括多项式拟合法、高次差法、MW组合(Melbourne-Wubbena,MW)法、电离层残差法等[2-7]。上述方法单纯利用GNSS(Global Navigation Satellite System,GNSS)观测值完成周跳探测,其中多项式拟合法、高次差法难以解决动态场景下的周跳问题;MW法在检验量中加入伪距参量,使该方法对小周跳不敏感[8];电离层残差法无法直接探测单一频点的周跳。同时,在动态情况下卫星信号信噪比较低,也增加了周跳探测的难度[9]。为此,许多学者将惯性导航参数融入周跳探测的算法中,以提高周跳探测能力[10-11]。文献[12]提出用惯导输出的高精度位置信息反解出星地距离,以代替GNSS伪距观测值,并利用宽巷组合与无电离层组合联立修复周跳;文献[13]提出基于INS(Inertial Navigation System,INS)辅助的无电离层组合和宽巷组合的联合探测方法;文献[14]将双频载波相位进行宽巷和超宽巷组合,并利用INS反解出双频惯导载波相位,联合构建无几何观测模型,降低观测噪声和多径效应的影响。上述方法均采用INS的位置信息预测GNSS观测值,随着时间的增加,预测误差累积严重,进而影响周跳探测结果的可靠性。
本文基于宽巷组合和电离层残差组合,提出一种INS辅助的动态双频周跳探测与修复方法。该方法利用INS的加速度信息和姿态信息,结合BDS双频载波相位观测值,通过站间差分、历元间差分等方法,推导了INS辅助的双频宽巷周跳检验量,对检验量的误差特性进行分析,并结合电离层残差组合实现周跳修复。
1 北斗双频周跳探测方法
周跳探测的实质在于判断载波相位观测值是否出现突变,构造能够反映观测序列微小变化的检验量。动态情况下,载体的变速运动同样会导致观测值发生剧烈变化,需要抑制加速度对检验量的影响,提高周跳探测结果的准确性。
1.1 INS辅助的周跳探测方法
短基线情况下,BDS载波相位的站间单差观测方程可表示为[15]
(1)
式中:下标ur表示对应参数的站间差分;λ表示对应频点的波长;ρ表示星地几何距离;N表示整周模糊度;ε表示观测噪声。
对BDS两个不同频点的φur做宽巷(Wide Lane,WL)组合可得
(2)
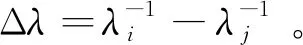
如图1所示,由参考站、移动站和卫星之间的几何关系可得
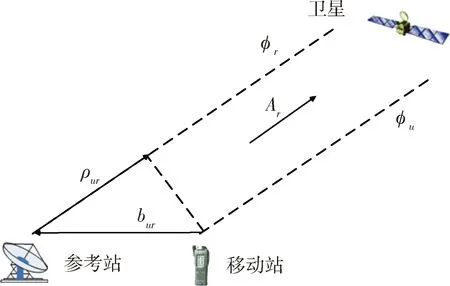
图1 站星几何关系示意图
ρur=-Ar·bur
(3)
式中:bur表示基线向量,Ar表示参考站到卫星的单位视线向量,于是式(2)可以表示为
(4)
对式(4)进行历元间一次差分得
(5)
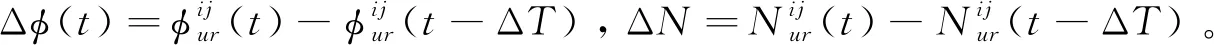
在卫星信号采样率较高时,两相邻历元间Ar近似不变,移动站相对参考站可认为是匀变速运动。因此,式(5)可记作
(6)
式中:νt=[bt-bt-ΔT]/ΔT。
对式(6)进行历元间二次差分得
(7)
式中:at+ΔT=[νt+ΔT-νt]/ΔT。
式(7)中a是相对地理坐标系下的加速度,而惯导中加速度计测量的是在载体坐标系下的加速度,因此,需要对载体系下的加速度进行坐标转换,同时去除其中的有害加速度项,补偿重力加速度,得到地理坐标系下的加速度
(8)
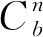
通过式(8)解算移动站在n系下的加速度后,由式(7)可得到INS辅助的宽巷组合检验量
(9)
当两频点的载波相位均无周跳时,检验量TINS-WL在0值附近波动;出现周跳时,TINS-WL将发生突变,突变历元为周跳发生的时刻。对于单频点周跳,突变值即为对应的周跳数值;对于双频点周跳,突变值即为两个频点对应的周跳值之差,因此该方法无法探测等周周跳。
INS辅助的宽巷组合周跳探测量可以消除载体运动导致的差分载波相位跳变,提高周跳探测的准确性,但是无法判断出周跳发生的频点和数值,因此需要联合其他的检测方法,固定周跳频点和数目,实现双频周跳探测与修复。
电离层残差法能够有效检测出等周周跳,因此在式(1)站间差分的基础上,对两个频点的载波相位观测方程作电离层残差组合,又称无几何距离(Geometry free,GF)组合
(10)
组合后的观测值与几何距离ρur无关,可以消除动态条件下载体运动导致的载波相位变化;并且站间差分消除了钟差、对流层延迟等误差项,削弱其对检验量的影响,提高周跳探测的精度。对φGF进行历元间差分后即可得到电离层残差法周跳检验量
(11)
1.2 周跳检验量误差分析
惯导辅助的周跳检验量不仅受载波相位观测噪声的影响,同时也受限于惯性设备的精度水平,需要分析INS误差对周跳检验量的影响水平。
由式(8)可知,b系下的加速度信息需要经姿态转移矩阵变换得到n系下的加速度。因此除加速度计自身的误差外,姿态误差也会影响加速度信息。
INS的姿态误差方程为
(12)
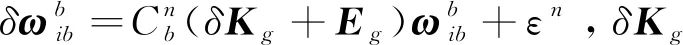
速度误差方程为
(13)
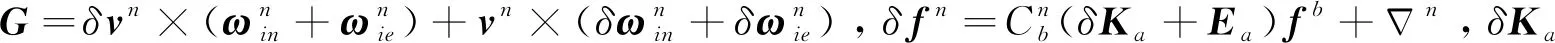
惯导系统量测值一般为速度增量,对速度误差微分即加速度误差方程
(14)
对于加速度计零偏为100μg、陀螺仪随机漂移为0.1(°)/h的惯导系统而言,在静止状态下,其加速度误差如图2所示。
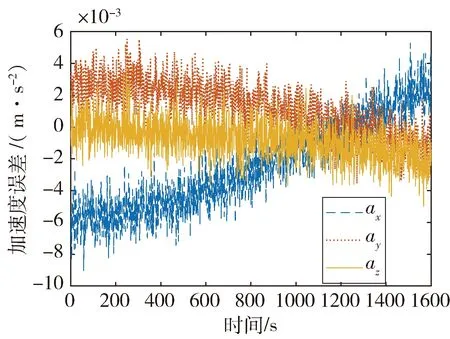
图2 INS加速度误差曲线
图2表明,1600s时间内,加速度误差随时间累积不超过10-3m/s2,累积误差对周跳检验量的影响可以忽略不计。
INS辅助的宽巷组合检验量TINS-WL的误差可以表示为
(15)
式中:σφ表示载波相位观测噪声,σa表示INS输出的加速度误差。
相应的电离层残差检验量TGF的误差可以表示为
(16)
2 双频载波相位的周跳修复
对于上述两种周跳探测方法,各自都存在难以探测出的周跳组合盲点。INS辅助的宽巷组合法无法探测出两频点在同一历元处发生的等周周跳;电离层残差法则无法探测出与其载波频率对应成比例的周跳组合。因此,需要将两种方法相结合,消除各自的探测盲点,同时确定周跳发生的频点和数值,实现北斗双频载波相位的周跳修复。
由式(9),检验量TINS-WL对应的Bi点Bj可以表示为
(17)
由式(11),检验量TGF对应的Bi和Bj频点周跳可以表示为
(18)
设参考站载波相位不存在周跳,则ΔNur即为对应的周跳值,对应频点发生的周跳值可以表示为
(19)
3 仿真校验
仿真校验中,采用GNS8330型多星座模拟器,选取BDS的B1和B2频点卫星信号,数据采样率设置为1Hz,采样时间为1600s。载波相位观测噪声为0.01周,电离层参数采用陆地电离层模型,对流层参数采用萨斯塔莫宁模型;惯导模拟解算中设置加速度零偏为100μg,陀螺仪随机常数设为0.1(°)/h。仿真设计流程如图3所示。
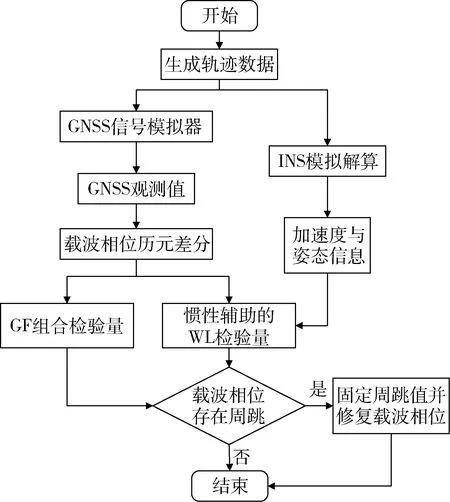
图3 算法仿真实现流程图
为了验证不同运动状态对周跳探测的影响,移动站的运动包含了动态场景下无人机滑行、爬升、平飞、转弯、降落等不同的状态,轨迹如图4所示。
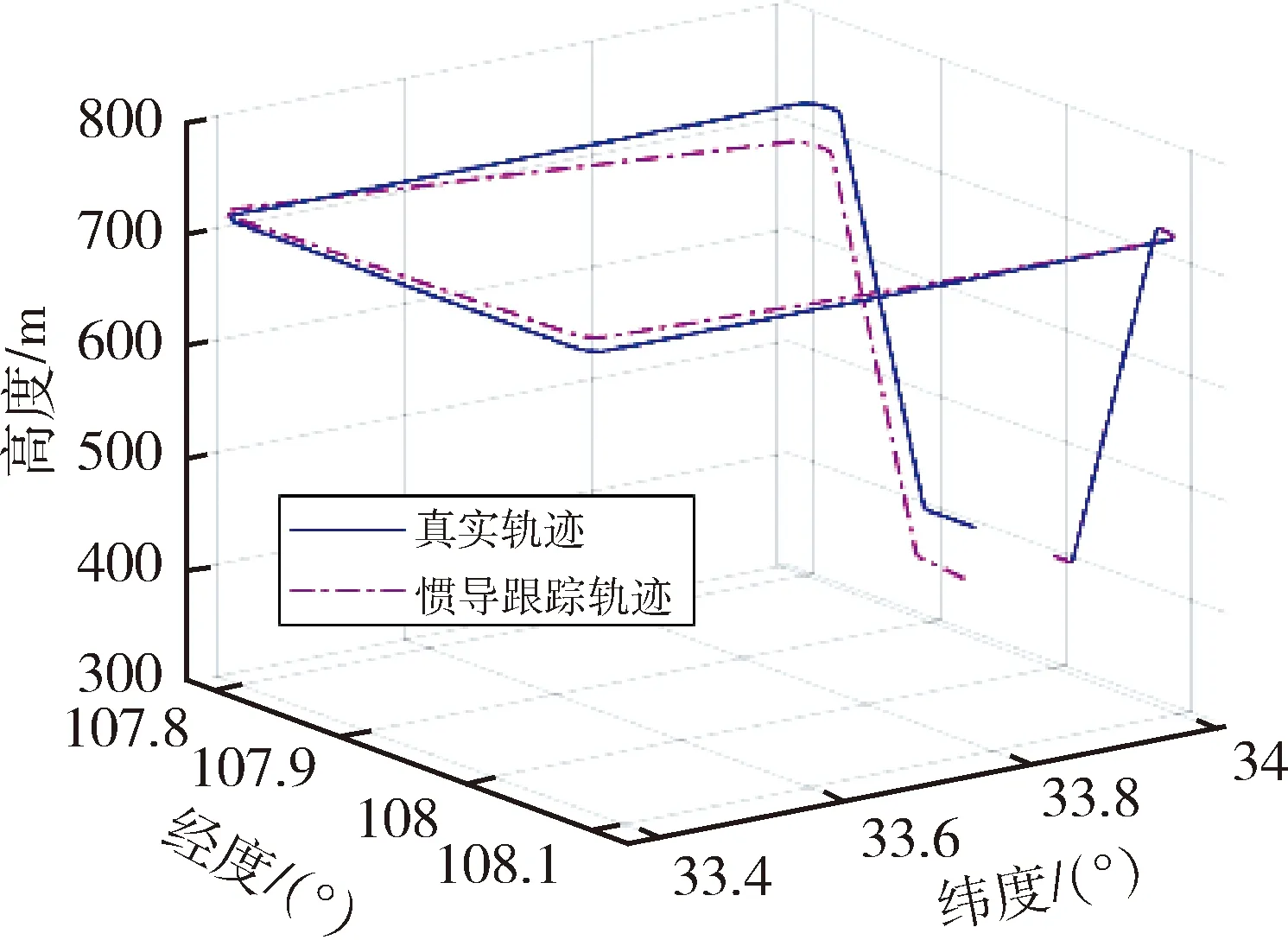
图4 模拟无人机飞行轨迹
之后利用轨迹数据完成惯导观测数据的模拟解算,得到站间相对加速度,如图5所示。
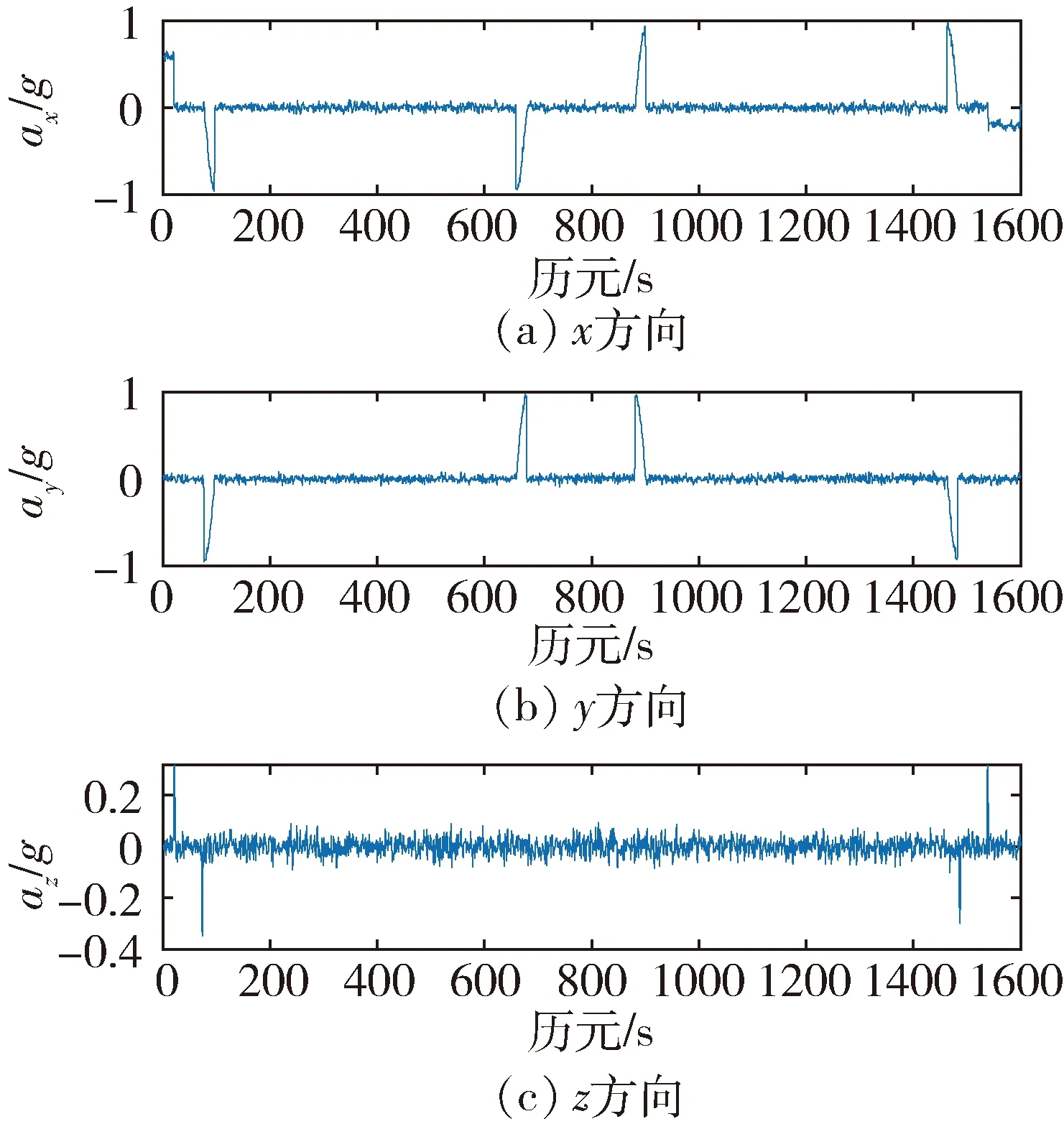
图5 站间相对加速度
BDS观测值由模拟器仿真得出,可以确保载波相位中不含有周跳。为了验证本文方法对不同类型周跳的探测性能,在移动站的载波相位观测值中加入表1所示的不同周跳组合。
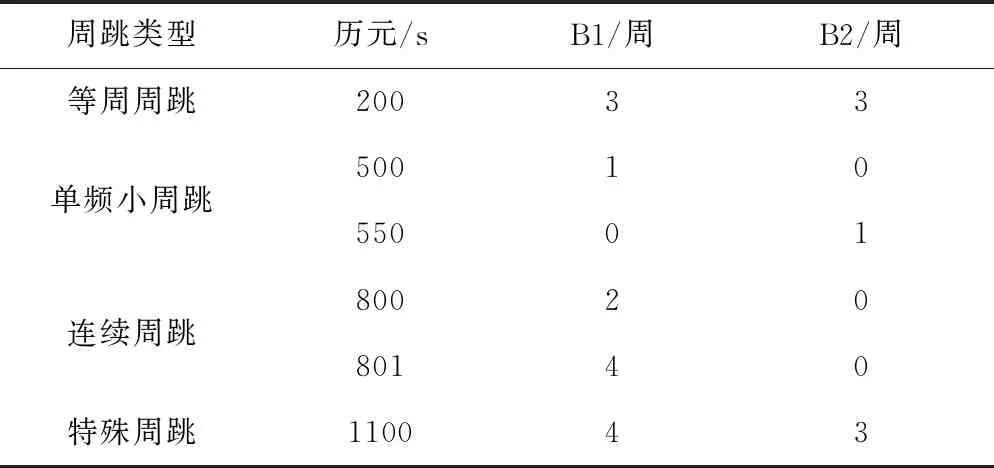
表1 不同类型周跳组合
采用INS位置坐标和卫星坐标反解出惯导伪距来辅助周跳探测的方法,惯导解算的位置误差随时间累积严重,如图6所示。
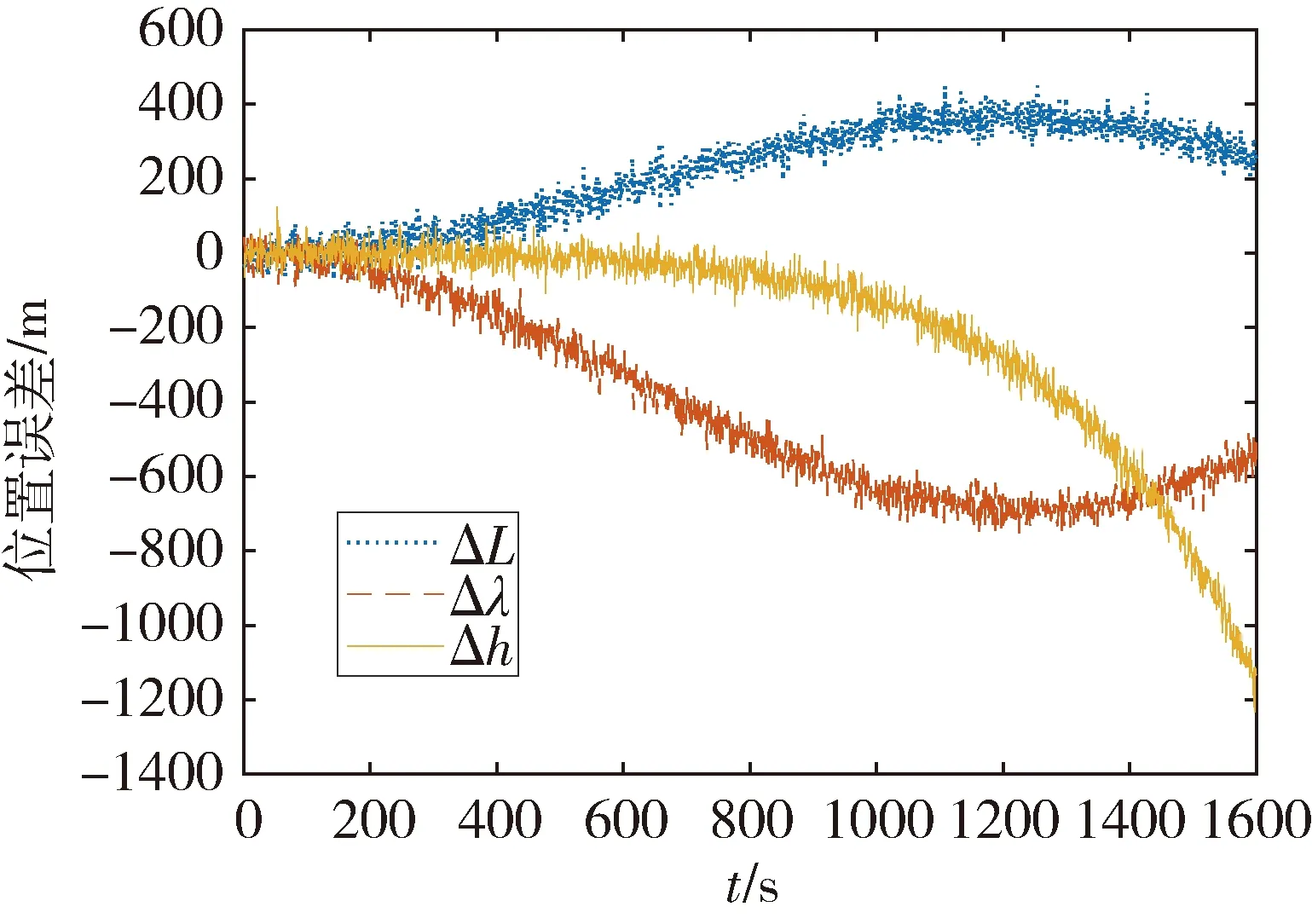
图6 INS位置误差曲线
用INS伪距替代MW组合周跳探测方法中的GNSS伪距,对组合观测值历元间差分构造检验量TINS-MW,探测结果如图7所示。
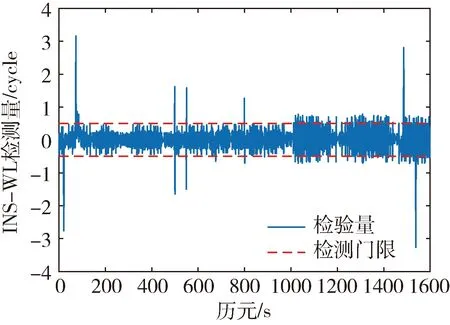
图7 INS辅助的MW检验量
图7表明,随时间增加,累积误差使检验量TINS-MW超出检测门限,无法探测小周跳,并且由于加速度导致的载波相位跳变与周跳相似,将使检测结果产生误判,降低周跳探测的成功率,影响后续历元的载波相位修复。
本文所提方法将B1和B2频点载波相位观测值作宽巷组合,之后对其进行历元间双差,即可得到宽巷组合检验量。当检验量超出三倍中误差σINS-WL时,即可判断该历元处载波相位观测值发生周跳,因此,根据式(15),检验量门限值设为0.47。周跳探测结果如图8所示。
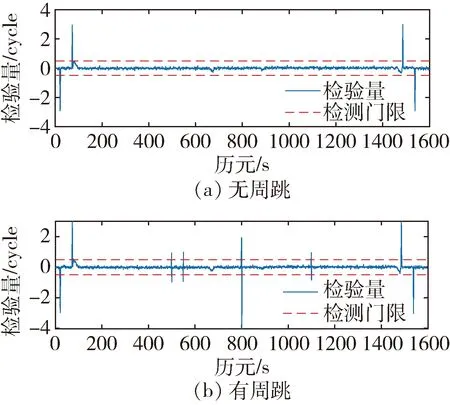
图8 宽巷组合检验量
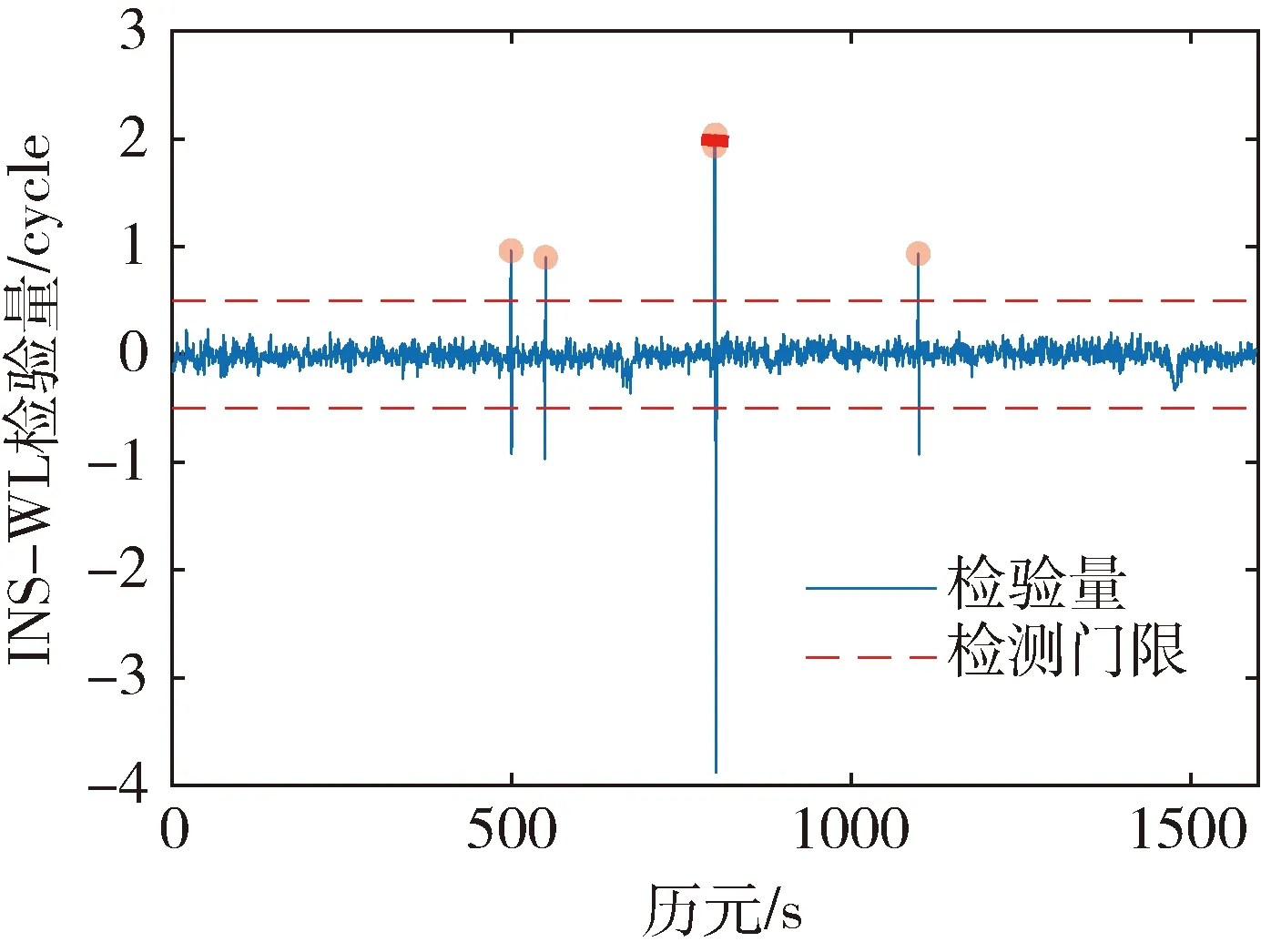
图9 INS辅助的宽巷组合检验量
可以看出,图9中检验量TINS-WL不含由加速度导致的粗差,仅剩由周跳引起的突变值。对照表1中加入的周跳组合可以看出,所提方法可以成功探测出小周跳、连续周跳和特殊周跳。等周周跳则需要联合改进电离层残差法进行检测,由式(16),检验量门限值设为0.09。电离层残差法探测结果如图10所示。
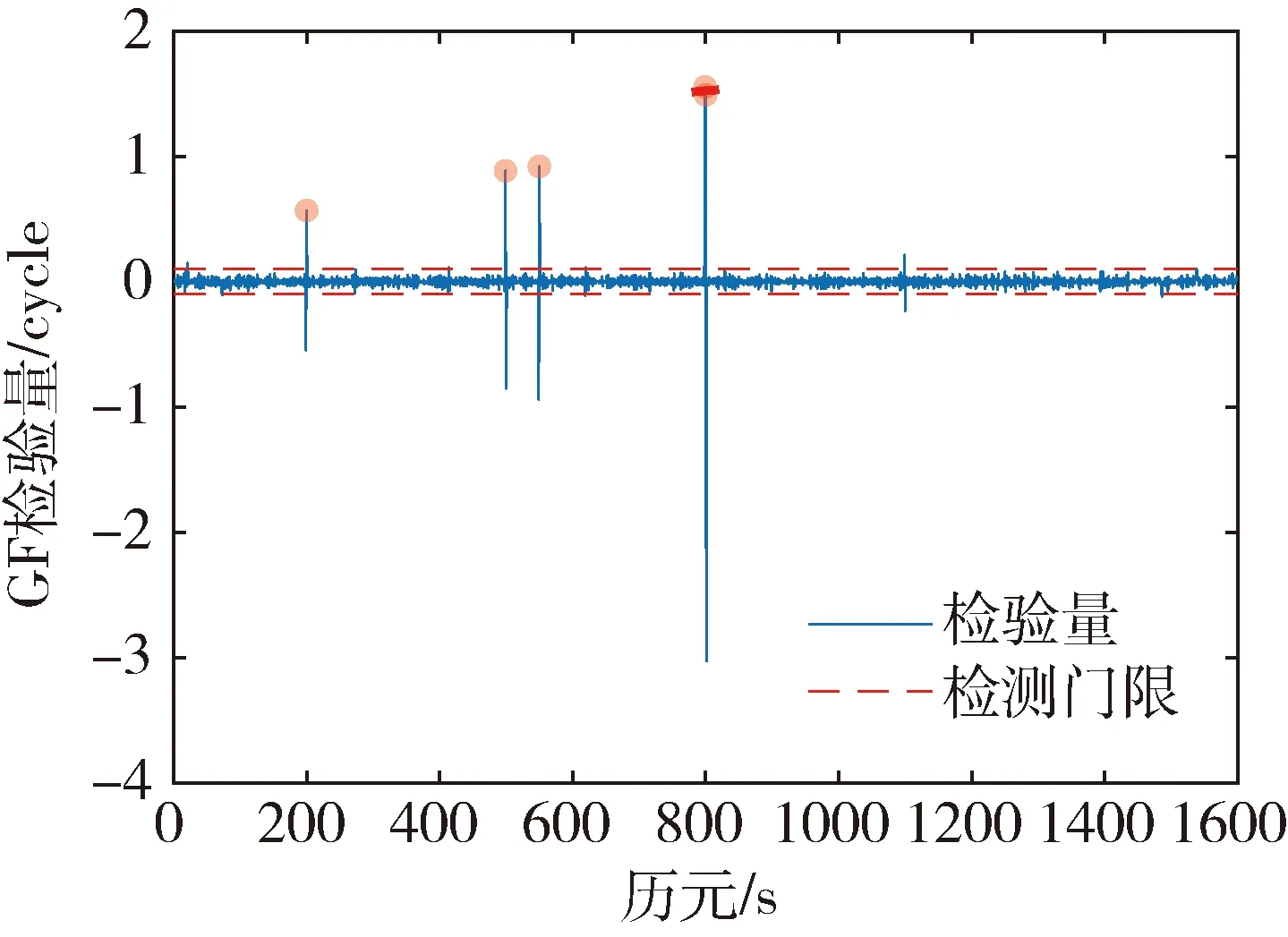
图10 电离层残差检验量
TGF在第200历元处的值超出门限值,表明探测出对应历元发生的等周周跳。综合两种方法,可以成功探测出表1中加入的多种类型周跳。
根据式(16),由TINS-WL和TGF解算出周跳值,并确定周跳发生的频点。周跳修复的结果如表2所示。
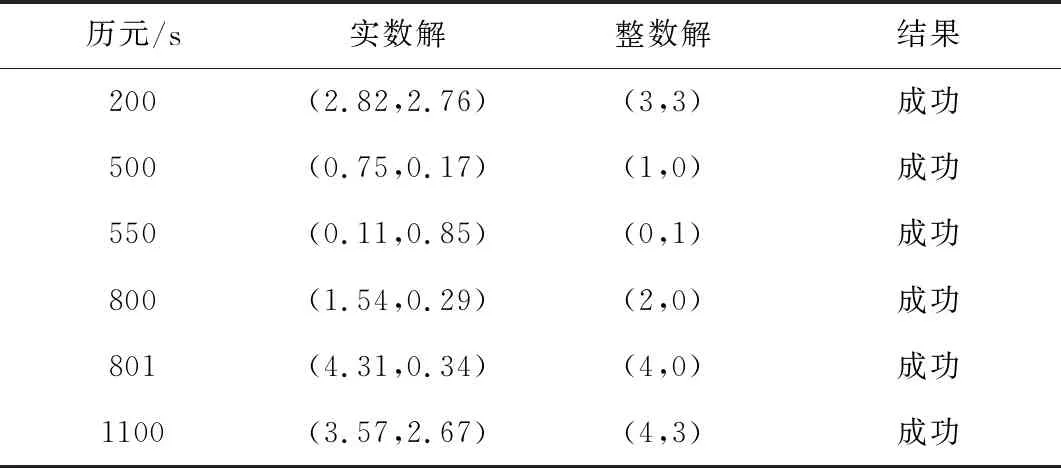
表2 周跳修复结果
表2表明,所提方法成功探测出等周周跳、小周跳、连续周跳以及特殊周跳,并且由检验量联合求解出的周跳值与设定值一致。
4 结论
提出了一种INS辅助的双频周跳探测与修复方法,在周跳探测过程中引入加速度信息,抑制了接收机运动状态导致的载波相位观测值变化,提高周跳探测能力。仿真实验表明,相比于INS位置信息辅助的周跳探测方法,提高了动态情况下的探测准确性,周跳探测的正确率达到100%;同时提高了探测的精度,能够准确探测出任一频点的1周小周跳。该方法结合电离层残差法可以修复不同频点、多种类型的周跳组合,具有一定的应用价值。

