精梳毛纺锭子转速神经网络反演研究

曹丽艳，陈 廷

(苏州大学纺织与服装工程学院，江苏 苏州 215021)

精梳毛纺加工过程的特点是工序复杂，成纱质量的好坏与加工设备、原料选择以及工艺设计等密切相关。为了提前预知成纱质量情况，方便进一步对加工过程实现有效调控，国内外不少专家、学者就此开展了研究与实践，并取得了较多的成果[1-2]。针对成纱质量的预测研究可以理解为在确定原料和设备工艺参数条件下，通过计算和求解加工系统提前得到产品质量指标[3]，但是针对毛纺纺纱参数的反演研究却少人问津。

纺织企业的生产经营离不开对生产成本的合理控制，这时候对成纱过程的逆向研究就显得尤为必要，在提高产品工艺设计针对性的同时，还要在保证产品质量要求前提下尽可能降低生产成本[3]。

精梳毛纺的纺纱参数和成纱质量指标间的关系属于非线性关系。目前大多数纺织企业在纱线的实际生产过程中，技术人员对于纺纱元件的调节力度并不大，通常情况下只是凭借经验调节锭子转速，但是仅凭经验实现成纱过程的调控，缺乏科学计算基础，容易造成生产出来的纱线质量不符合目标需求的后果[4]。

针对精梳毛纺的纺纱参数反演研究可以理解为非线性问题的最优化改进方案。在所有的非线性反演研究中，利用穷举法选择输入参数通常被认为是最有效和最直接的方法，但是这种方法的使用范围较为局限，比如面对海量数据的筛选和优化时工作量大到难以完成，哪怕通过计算机处理也是见效甚微。因此本文提出首先采用合适的数据优选方法确定输入参数，再通过神经网络进行验证分析，这在国内外反演领域内也一度成为研究热点。

纱线生产过程中，所有纺纱参数和纱线质量之间时刻发生着不定向变化，两者之间的函数关系难以确切表达出来。本文采用输入对输出影响程度的数据优选方法得出不同成纱质量指标和锭子转速的关系密切程度，以此确定神经网络的输入参数，通过构建神经网络反演模型对优选结果实现验证分析，为进一步优化工艺奠定基础。

1 实验测试

本次试验原料为羊毛纤维，测试环境条件为温度(20±2) ℃，相对湿度(65±3)%，羊毛纤维在测试环境中平衡24 h后再测试纤维性能指标。实验使用Uster-3型乌斯特测试仪测试成纱条干不匀率、细节和粗节，采用YG020A型电子单纱强力仪测试成纱断裂强度和断裂伸长率；本次共采集23组试样，成纱质量指标7个，分别是断裂强度(cN/tex)、断裂强度不匀率(%)、断裂伸长率(%)、断裂伸长不匀率(%)、粗节(+50%/km)、细节(-50%/km)和条干不匀率(%)。成纱质量指标和锭子转速见表1。

表1 成纱质量指标和锭子转速

2 输入参数优选

考虑到神经网络本身的运行特性，输入参数越多越容易致使网络性能不稳定，运行和收敛速度慢，可能进一步造成反演结果精确度和可信度过低。所以本文采用输入对输出影响程度的数据优选方法筛选出与锭子转速关联性较大的成纱质量指标作为显著影响因子，数据优选排序靠后的成纱质量指标作为非显著影响因子，通过把显著影响因子作为神经网络的输入参数，提高网络模型的稳定性和收敛性能，同时提升模型反演的精确度和结论可信度。

2.1 输入对输出影响程度的数据优选方法

为研究输入参数的变化趋势对输出参数的影响程度，Chen等[5]提出以下两个假设：(1)如果一个输入变量参数发生微弱的变化，导致输出变量参数发生显著的变化，那么，一般把这个输入变量参数叫作敏感变量参数[5]；(2)如果一个输入变量参数发生显著的变化，结果输出变量参数发生微弱的变化，那么，一般把这个输入变量参数叫作非敏感变量参数[5]。运用文献[5]优选理论可计算出锭子转速神经网络输入参数优选结果。

2.2 锭子转速神经网络输入参数排序结果

成纱质量指标和锭子转速的敏感值见表2。

表2 锭子转速神经网络输入参数优选结果

采用输入对输出影响程度的数据优选方法对成纱质量指标排序见表2。

由上表最终排序结果可以知道，与锭子转速关系最为密切的前4个输入参数为：断裂强度、断裂伸长不匀率、断裂强度不匀率、断裂伸长率。密切程度相对靠后的4个输入参数为：断裂伸长率、细节、粗节和条干不匀率。

3 锭子转速神经网络反演模型的构建

3.1 BP神经网络设计

早在20世纪就有研究者证明：采用单隐层BP网络可以实现任意封闭区间内非间断函数的连接，由此不难得出三层结构的神经网络可以满足多维到多维的映射[6]。本文采用的BP神经网络反演模型就是三层网络结构，输入层4个神经元，隐层3个神经元，输出层1个神经元，网络结构为4-3-1，如图1所示。

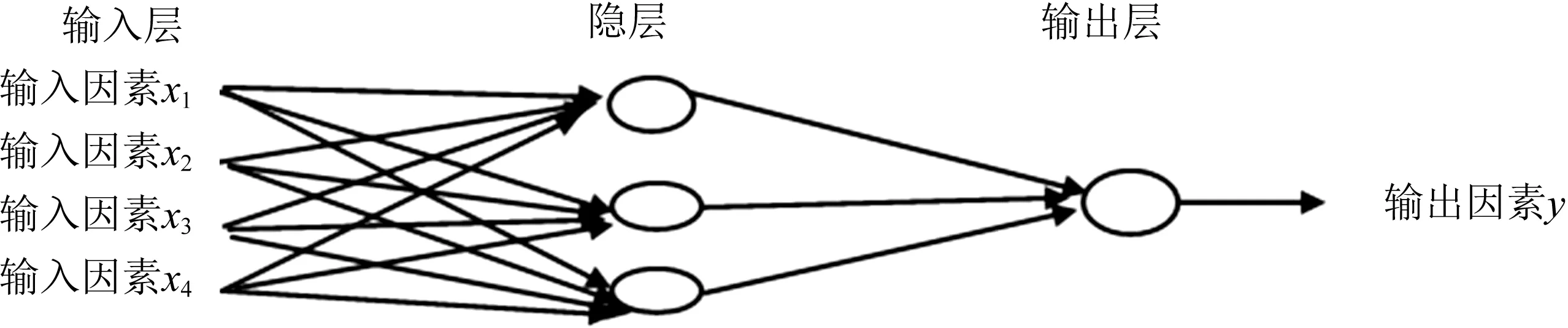
图1 神经网络反演模型示意图

输入层神经元分别对应的是断裂强度、断裂伸长不匀率、断裂强度不匀率、断裂伸长率这4个质量指标，输出层神经元对应锭子转速参数。采用不同函数训练网络，运行结果会略有不同，本文采用“trainlm”函数训练和调整精梳毛纺锭子转速神经网络权值和阈值，采用正切S型和线性函数实现网络传递；网络参数配置如下：设置网络误差l×10-3，设置训练步数l×104。

3.2 构建反演模型验证优选结果有效性

通过建立精梳毛纺锭子转速反演模型对优选结果可靠性加以验证，运用Matlab(R2017a)软件工具实现编程。本文研究以成纱质量指标作为输入参数，以锭子转速作为输出参数，具体数据见表1；针对锭子转速建立两个神经网络反演模型，两个反演模型的输入参数有所区别，一个反演模型的输入参数采用排序前4位的成纱质量指标，分别是断裂强度、断裂伸长不匀率、断裂强度不匀率、断裂伸长率，余下一个反演模型采用排序靠后4位的成纱质量指标，分别是断裂伸长率、细节、粗节和条干不匀率。

通过观察验证结果对比实际值，分析得出前后两个神经网络的反演误差大小；假设以排序前四位的成纱质量指标作为输入参数建立的反演模型反演精度高于以排序后4位成纱质量指标作为输入参数建立的反演模型，那么可以认定采用输入对输出影响程度的数据优选方法得到的优选结果是可靠的，反之则可以认定为不可靠。

本文通过使用Matlab(R2017a)进行编程建模，从共计23组试验数据中选用具备代表性水平数据(即为试样11#、12#、13#和21#)作为测试水平组用以测试网络，剩下的19个试样用以训练网络，实现锭子转速的反演研究，结合反演值和实际值进行比对分析。

输入对输出影响程度排序在1～4的成纱质量指标作输入参数时，锭子转速的反演值和实际值误差为4.95%(表3)；输入对输出影响程度排序在4～7的成纱质量指标作输入参数时，锭子转速的反演值和实际值误差为7.33%(表4)；可知采用排序前4位的成纱质量指标作为精梳毛纺锭子转速神经网络的输入参数时，锭子转速的反演值和实际值误差值更小，反演结果更精确，这说明采用输入对输出影响程度的数据优选方法得到的优选结果是可靠的。

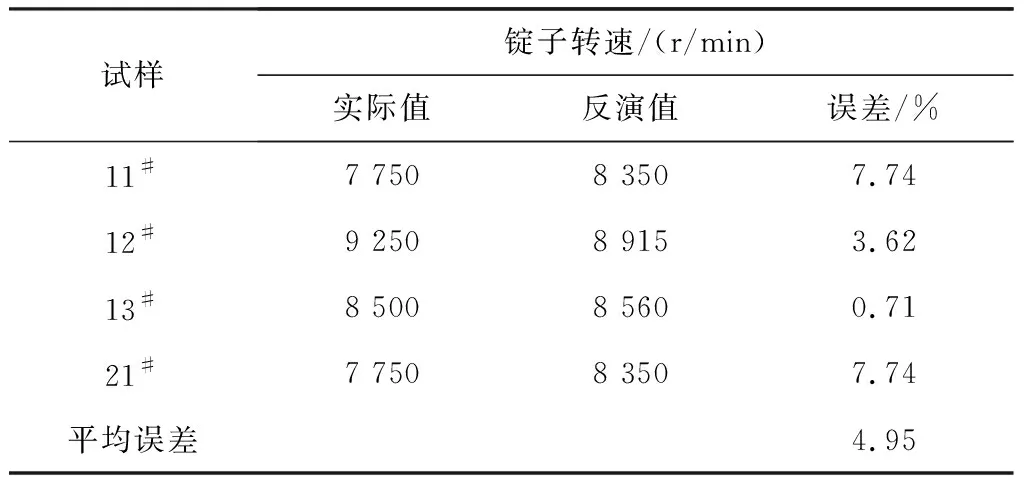
表3 输入对输出影响程度排序在1～4的成纱质量指标作输入参数时的反演结果

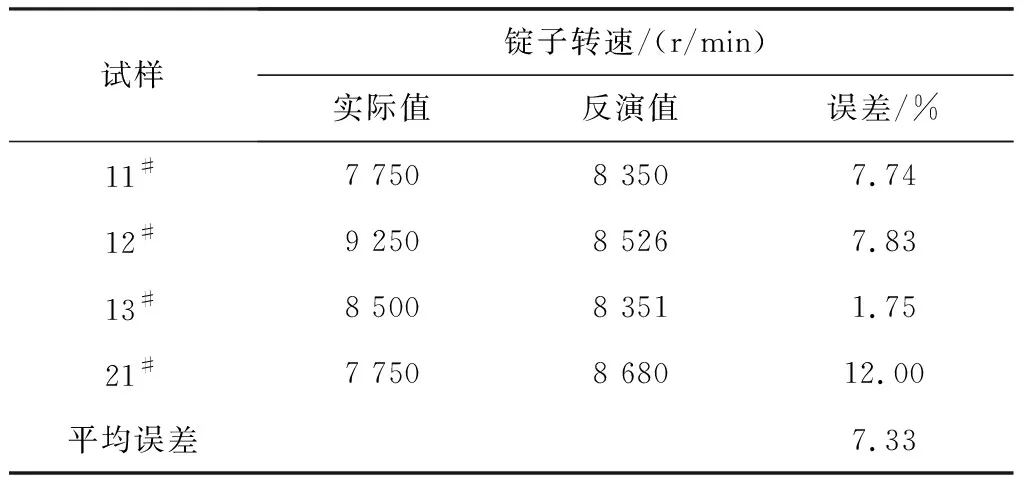
表4 输入对输出影响程度排序在4～7的成纱质量指标作输入参数时的反演结果

最后，仔细观察表中数据可以发现，试样11#和21#的反演误差较其他试验样本的反演误差较大，

究其原因，源于训练网络中类似样本的数量较小，进而影响了反演模型的精确性。

4 结论

通过数据优选结果确定输入参数构建两个4-3-1网络结构的BP神经网络模型，模型以锭子转速作为输出参数，实现纺纱参数的反演研究，验证结果表明，优选结果有效且可靠。结果显示，两个模型的反演值与实际值误差均控制在10%以内，反演精度较高，所以可以确定，利用神经网络原理构建精梳毛纺锭子转速反演模型是切实可行的。依据反演结果动态调控加工过程，优化工艺，提高产品质量，同时对企业新产品工艺设计的快速决策也具有很好的借鉴作用。

实践证明，成纱质量指标与锭子转速的关联程度有大有小，加之在数据的实际采集中能获得的样本量容易受到限制，故采用有限的数据样本建立纺纱参数神经网络反演模型已经成为本领域研究工作的现实需求。