两类交叉四角链的拉普拉斯谱及其应用
涂淑玲,王广富
(华东交通大学理学院,江西 南昌 330013)
在图论中, 拉普拉斯矩阵是图的一种矩阵表示,定义为图的度矩阵与邻接矩阵的差。 拉普拉斯矩阵的所有特征值称为图的拉普拉斯谱。 拉普拉斯谱及其应用可以解决复杂网络中的许多理论问题[1-2],网络的拉普拉斯谱的计算在拓扑结构和动力学等方面有诸多应用。 例如,在化学上,对于用来反映化合物分子结构的基尔霍夫指标已有 广 泛的研 究。 1993 年,Klein 等[3]提 出 了 一 个 新的距离函数——电阻距离。 图的每条边等价于一个单位电阻,然后利用欧姆定律计算出任意两个顶点之间的有效电阻,即电阻距离;图中所有顶点对之间的电阻距离之和定义为图的基尔霍夫指标。 网络的基尔霍夫指标可以用非零拉普拉斯特征值的倒数之和来表示[4];网络的生成树数目可以由所有非零拉普拉斯特征值的乘积来确定[5];网络的直径可以由拉普拉斯矩阵的第二小特征值来估算[6]。 尽管从分析的角度,拉普拉斯谱的计算只是一个理论上的挑战,但建立网络的拉普拉斯谱是很有意义的。 近二十年来,有很多人在研究各类分子图的拉普拉斯谱的计算及其应用[3,4,7-11]。 Yang等[12]研究了线性六角链的部分拉普拉斯特征值,从而确定了其基尔霍夫指标。 之后, 人们通过Yang 等[12]的方法得到了其他一些分子网络的部分拉普拉斯特征值及基尔霍夫指标,如苯环[13]、五边形链[14]等。 Pan 等[15]研究了线性交叉多联骨牌链(即线性交叉四角链) 的部分拉普拉斯特征值、基尔霍夫指标及生成树数目。 直接计算出某图类的所有的拉普拉斯特征值还是很困难的。 本文主要研究并确定了线性交叉四角链和交叉四角柱状链两类图的拉普拉斯谱,更简便地得到了这两类图的基尔霍夫指标及其生成树数目表达式。 另外,还利用交叉四角柱状链的拉普拉斯谱,推导出交叉四角柱状链的度-基尔霍夫指标的表达式。
1 预备知识
本文考虑的均为连通无向图,即图中任意两个顶点都存在路径使其连通。 设图G=(V,E),V={1,2,…,n}和E={e1,e2,…,em}分别为图G 的顶点集和边集。 di表示顶点i 的度,i=1,2,…,n。 文中未加说明的符号以及定义等参见文献[16]。
定义1.1 图的拉普拉斯矩阵是指由顶点集V作为行和列进行索引n×n 的矩阵,记为L(G)=(lij),其中

定义1.2 拉普拉斯矩阵L(G)的所有特征值称为图G 的拉普拉斯谱;若L(G)的特征值为λ1≥λ2≥…≥λn-1>λn=0, 那么图G 的拉普拉斯谱可记为S(G)=(λ1,λ2,…,λn)。
定义1.3 设H1=(V1,E1),H2=(V2,E2)是两个顶点集不相交的简单图,对顶点集V=V1×V2(即V1与V2的卡氏积) 中的任意两个点u=(ui,vj) 和v=(up,vq),当ui与up相邻或者ui=up且vj与vq相邻时就将u 和v 连一条边所得到的图。 称之为H1与H2的合成图,记为H=H1[H2]。
定义1.4 图G 的一个生成子图若是一棵树,称为图G 的一棵生成树。
定义1.5 将图G 看成一个电网络N 且图G的每条边等价于一个单位电阻,然后计算出电网络N 中任意两个顶点i 与j 之间的有效电阻,即顶点i与j 之间的电阻距离,记为rij[3]。

Hou 等[19]得到了任意两个图的合成图的拉普拉斯特征值和生成树数目的表达式,其中结构相同而标号不同的生成树视为不同的生成树。
引理1.9 设H=H1[H2],其中|V(H1)|=s,|V(H2)|=t,若S(H1)=(0,μ1,…,μs-1),S(H2)=(0,ω1,…,ωt-1),图H1的度序列记为d(H1)=(d1,d2,…,ds),那么H=H1[H2]的拉普拉斯特征值是0,tμi(i=1,…,s-1),tdl+ωj(l=1,…,s;j=1,…,t-1)[19]。
引理1.10 设H=H1[H2],那么的生成树数目τ(H1[H2])的值为[19]

如图1 所示, 设Xn是由n 个完全图K4构成且经过适当标号的一条线性交叉四角链;Gn是由n 个完全图K4组成的交叉四角柱状链, 其平面展开图如图2(a)所示,G6的立体图如图2(b)所示。
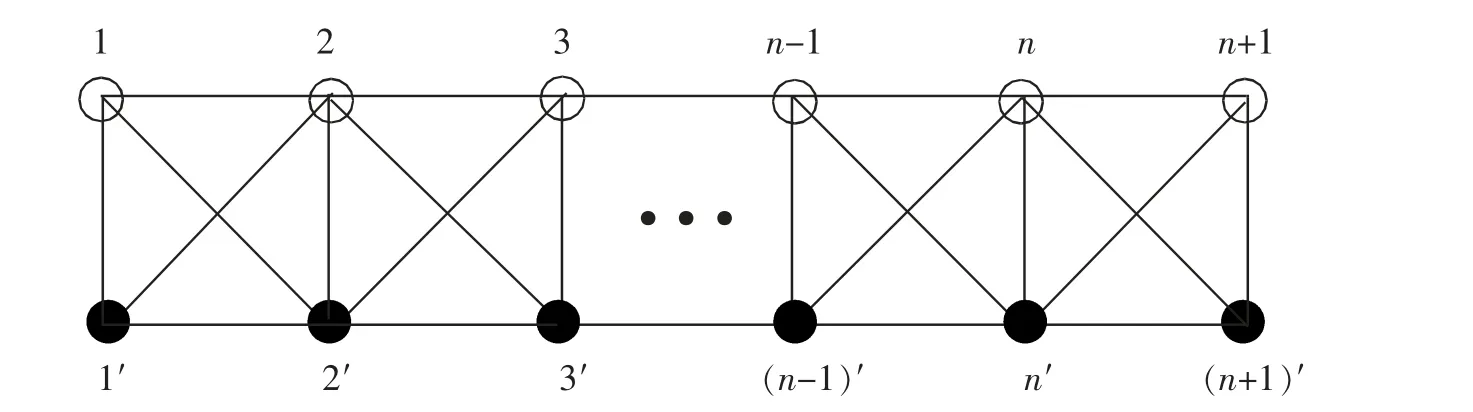
图1 线性交叉四角链XnFig.1 Linear crossed polyomino chain Xn

图2 交叉四角柱状链Fig.2 Crossed polyomino cylinder chain
可以发现:Xn可看成是一条路与K2的合成图,即Xn=Pn+1[K2],其中Pn+1表示一条n+1 个顶点的路;Gn是具有n 个顶点的圈Cn与K2的合成图, 即Gn=Cn[K2]。
2 线性交叉四角链Xn 的拉普拉斯谱及其应用

下面是Xn的拉普拉斯谱的两个应用。
2.1 Xn 的基尔霍夫指标
定理1 设Xn为线性交叉四角链,则
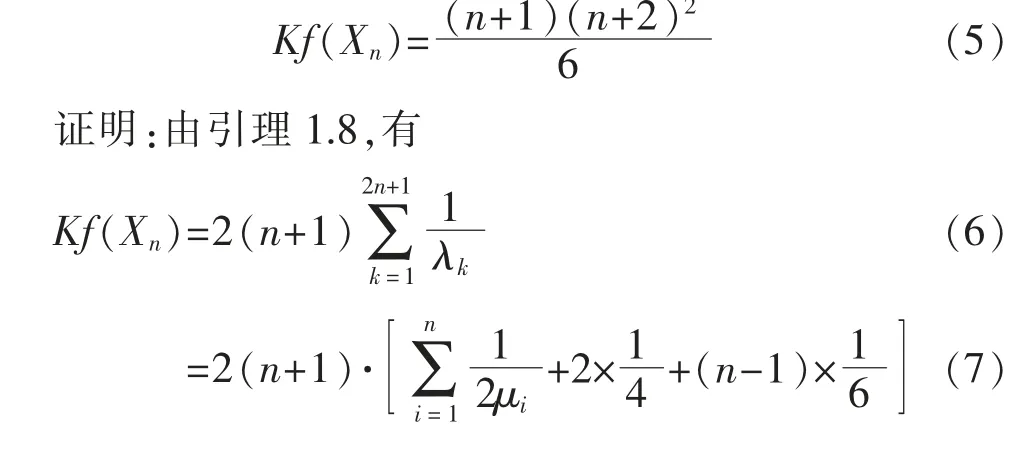
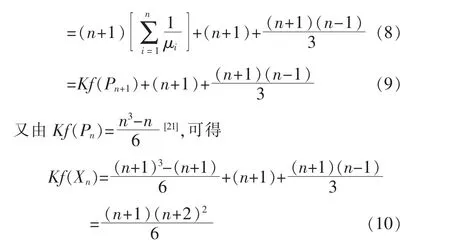
2.2 Xn 的生成树数目
定理2 若用τ(Xn)表示线性交叉四角链Xn生成树的数目,则

定理得证。
实例验证:当n=1 时,交叉四角链X1即为K4,

故,结论成立。

图3 X1Fig.3 X1
下面计算出了线性交叉四角链从X1到X50的基尔霍夫指标,如表1 所示,从X1到X20的生成树的数目如表2 所示。

表1 线性交叉四角链从X1 到X50 的基尔霍夫指标Tab.1 Kirchhoff indices of linear crossed polyomino chain from X1 to X50
3 交叉四角柱状链Gn 的拉普拉斯谱及其应用
与上一部分相同, 先利用引理1.9 计算Gn的拉普拉斯谱。

3.1 Gn 的基尔霍夫指标

结合定理1 和定理3,得到以下推论:
推论 设Xn和Gn分别为线性交叉四角链和交叉四角柱状链,则

3.2 Gn 的生成树数目
定理4 设τ(Gn)为交叉四角柱状链Gn生成树的数目,则

证明:由于Gn的生成树数目为n,根据引理1.10,

3.3 Gn 的度-基尔霍夫指标


图4 G1Fig.4 G1

结论得证。
下面也列出了交叉四角柱状链从G1到G50的基尔霍夫指标及从G1到G20的生成树的数目,分别如表3 和表4 所示。

表3 交叉四角柱状链从G1 到G50 的基尔霍夫指标Tab.3 Kirchhoff indices of crossed polyomino cylinder chain from G1 to G50

表4 交叉四角柱状链从G1 到G20 的生成树的数目Tab.4 The number of spanning trees of crossed polyomino cylinder chain from G1 to G20
4 结论
1) 本文利用图的合成运算,得到了线性交叉四角链Xn和交叉四角柱状链Gn的拉普拉斯谱。
2) 通过应用拉普拉斯谱,得到了这两类交叉四角链的基尔霍夫指标、生成树数目的表达式。
3) 利用正则性得到了交叉四角柱状链的度-基尔霍夫指标的表达式。
4) 这些表达式对这两类图的拓扑性质提供了更深入的理解。

