基于放大系数和权重组合的无砟轨道TQI 计算
许玉德,吴琰超,魏子龙,杨 飞
(1.同济大学道路与交通工程教育部重点实验室,上海 201804;2.中国铁道科学研究院集团有限公司基础设施检测研究所,北京 100081)
轨道质量指数 (track quality index,TQI) 是指200 m 单元区段内轨道的左高低、右高低、左轨向、右轨向、轨距、水平和扭曲等7 项不平顺的标准偏差之和,通过将全线分为若干个单元进行计算后得到TQI 的平均值,以表示线路的整体状态[1-2]。 然而,随着无砟轨道在中国高铁的广泛应用,TQI 表现出了一定的不适应性[3]:在对轨道状态的检测中发现,轨道局部波动不能被有效识别,存在潜在轨道病害被遗漏的现象; 在工务实践中, 管理人员仅对TQI超限地段进行轨道管理,对上述各单项标准差超限值的关注较少,导致某些区段评价的失真;特别是在高速铁路无砟轨道平顺性较好的情况下,不同线路的TQI 平均值相差很小,难以对不同线路平顺状态的优劣进行合理地比较。 寻找更合理的评估方法对于科学评价轨道服役状态,精准指导养护维修作业,进而保障高速铁路安全平稳运行具有重要的意义。
为改进现行区段管理标准的不足,众多国内外铁路机构与学者开展了不同形式的修订和完善工作。 许玉德等[4-7]先后提出了过程性能指数(process performance index,PPI)、 轨道几何状态均匀性指数(track geometry equality index,TGEI)、 轨道几何状态综合评价指标 (track geometry comprehensive index,TGCI)等评价方法,并对高速铁路无砟轨道几何不平顺区段管理长度进行了研究。 陈勋[8]通过统计分析方法对沪宁城际轨道质量指数的分布规律进行了研究,发现TQI 服从对数正态分布。 杨飞等[9]引入滑动标准差计算方式对轨道区段状态进行评价,结果表明滑动标准差能够找到轨道质量最差的区段并且识别不良区段的起止位置。 许贵阳等[10]利用LVQ 神经网络和层次分析法及聚类分析, 建立了基于TQI、轨检车单项几何不平顺、轨检车车辆加速度、晃车仪加速度、添乘仪加速度和人体感觉参数共6 项指标作为特征参数的轨道单元质量状态评价方法。Huang 等[11]综合静态检查、机车搭载式检查仪和轨检车获取的检测数据,提出了轨道综合质量 指 标 (track integration quality index,TIQI)。Sadeghi 等[12]根据轨距、高低、水平、扭曲等几何形位实测数据呈正态分布的特点,提出了基于平均值和标准差的轨道几何形位指数,该指标不仅能够评价单个参数,也给出了整个轨道几何形位的状态。 田新宇等[13]基于多体动力学理论和综合检测列车实测数据,探讨了300~350 km/h 高速铁路轨道长波高低不平顺管理标准和评价方法建议。 杨翠平等[14-15]提出了轨道加权质量指数 (track weighed quality index,F-TWQI),通过带通滤波对轨道不平顺波形分量的标准差赋权;并且利用主成分分析法对特征变量进行筛选,快速精简地获得轨检数据所包含的轨道状态信息, 实现对轨道线路潜在病害位置的识别。 高望翰[16]基于时频分析方法对轨道高低不平顺数据进行分析,提出了基于小波能量谱的轨道板结构状态评估算法,通过检测里程和波长的时频谱峰值确定轨道板病害。 Choi[17]使用机器学习的方法处理分析车辆振动加速度数据对轨道质量指数进行预测,提高了预测的效率。
TQI 在我国已应用多年, 在轨道区段质量状态评价中发挥了巨大的作用,工务管理实践中已经习惯运用TQI 来管理线路动态质量。 然而,在评价高速铁路无砟轨道不同线路区间时,TQI 差值很小,无法反映线路状态的差异,给无砟轨道精细化管理带来新的问题。 基于此,本文对TQI 的计算方法进行改进,提出了一种基于放大系数和不同权重组合的TQI 值计算方法, 对TQI 中的各单项分量赋予相应的权重,并将TQI 波形进行合理地放大,更加突出平顺性较差的区域,最后结合加拿大轨道单项几何参数指数的计算原理,扩大值域范围,以期对高速铁路无砟轨道线路平顺性进行更好地评估和管理。
1 权重系数
1.1 单项分量在TQI 中的比重
TQI 是用200 m 单元区段内的7 项轨道不平顺的标准偏差之和计算得到的,计算公式[18]如下
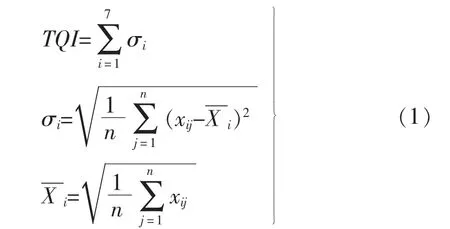
式中:σi为各项几何参数的标准差,其中i=1,2,…,7,分别表示左高低、右高低、左轨向、右轨向、轨距、水平和扭曲;xij为单元区段内各项几何偏差的幅值,其中j=1,2,…,n,n 为采样点的个数(200 m 单元区段中n=800)。
从式(1)中可以看出,组成TQI 的7 个单项分量的权重都为1,这表明7 个单项分量对TQI 的“贡献率”是相同的。 为获取各单项分量的实际“贡献”程度, 以某无砟高速铁路在2011—2020 年的轨道检测数据为例, 计算长度为120 km 的线路区段中各项分量占TQI 的比重,计算结果见表1。
从表1 中可以看出,各项分量的数值在TQI 中所占的比重从大到小依次为:扭曲(18.20%)、左右高低 (15.31%、14.94%)、 水平 (14.55%)、 轨距(13.89%)、左右轨向(11.64%、11.48%),说明扭曲标准差对TQI 计算结果的影响是最大的,其次是高低和水平标准差,轨距和轨向标准差对TQI 计算结果的影响最小。 可见,不同分量在TQI 中所占的比重各不相同,需要找到合适的方法对单项标准差赋予不同的权重,在利用TQI 对线路整体状态进行评价时突出对TQI 计算结果影响较大的成分。
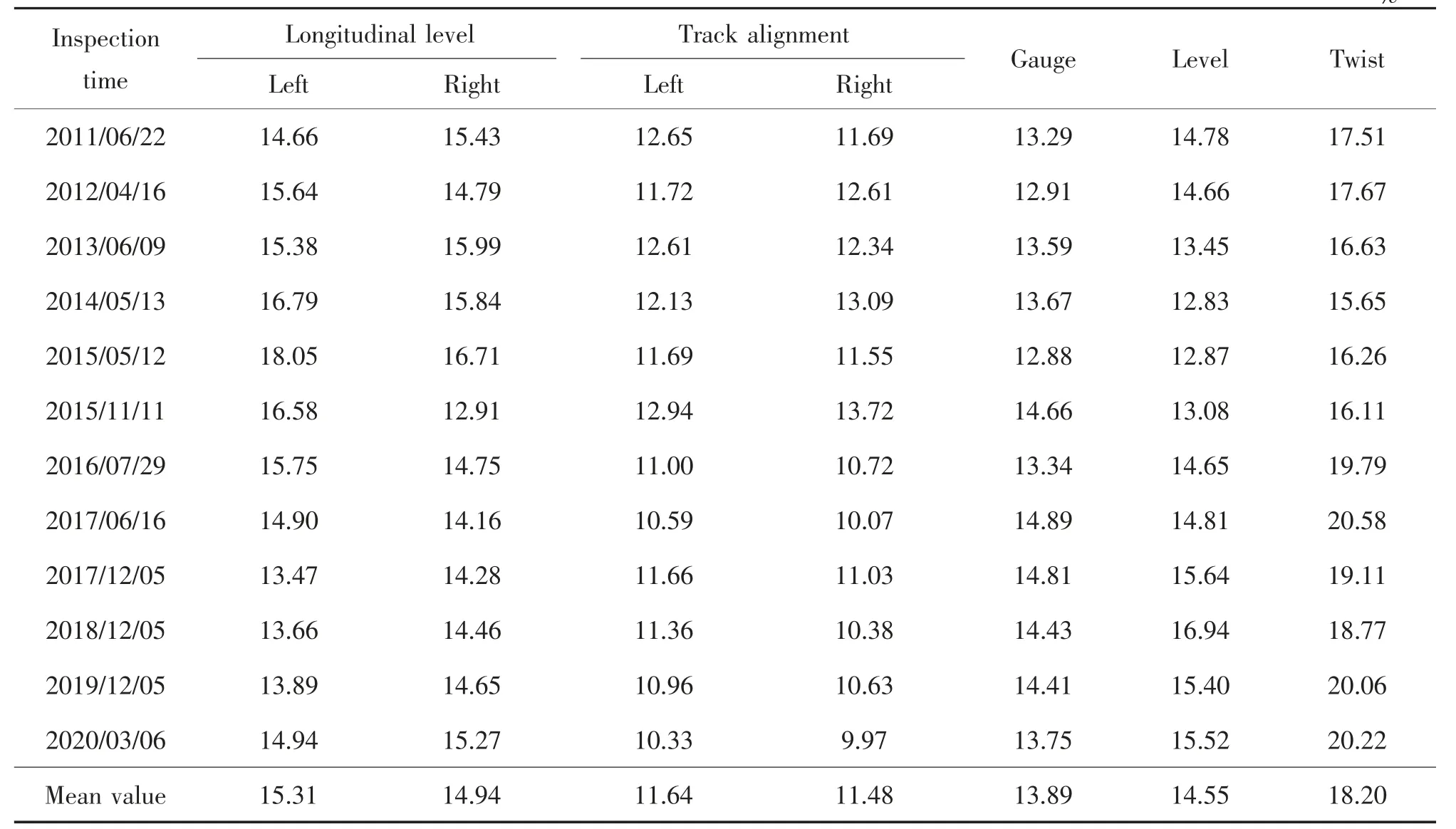
表1 某无砟高速铁路TQI 中各项分量占比Tab.1 Proportion of each component in TQI of a ballastless high speed railway %
1.2 变异系数
为了突出对TQI 计算结果影响较大的成分,使得其在TQI 中所占的权重更大,文章引入了统计学中的变异系数[19](coefficient of variation)概念。 变异系数是衡量观测值离散程度的统计指标,消除了平均值对数据离散程度的影响,反映了单位均值上的离散程度。一个线路区间内的单项分量变异系数cvi等于该线路上所有200 m 单元区段的单项标准差的标准差Si与单项标准差的平均值σi之比, 计算公式如下

采用式(2)的计算方法,统计某无砟高速铁路历年TQI 各项分量的变异系数,结果如表2 所示。

表2 历年TQI 各项分量的变异系数Tab.2 Variation coefficient of each component in TQI over years %
单项分量的变异系数反映了单项分量的离散程度,变异系数越大表示该线路区间内的单项标准差越离散。 如表3 所示,各项分量的变异系数在大多数时候从大到小的排列顺序依次为:轨距、水平、扭曲、高低、轨向,说明在该条线路上,轨距标准差的波动较大,但线路的TQI 值并不能有效识别该项波动,单纯使用TQI 的平均值并不能代表该线路的整体状况。
1.3 单项分量的权重
通俗上来讲,单项分量的数值较大反映了线路区域整体上该项不平顺较差;而单项分量的变异系数较大则反映了该项不平顺在该线路区域上时好时差。 为了有效识别这种轨道局部波动,变异系数较大的单项分量应占据较大的权重。 采用变异系数所占的百分比来分配TQI 的权重,如式(3)所示。

式中:αi为单项分量的权重。
根据式(3)的计算方法,统计某无砟高速铁路历年TQI 各项分量的权重系数,如表3 所示。
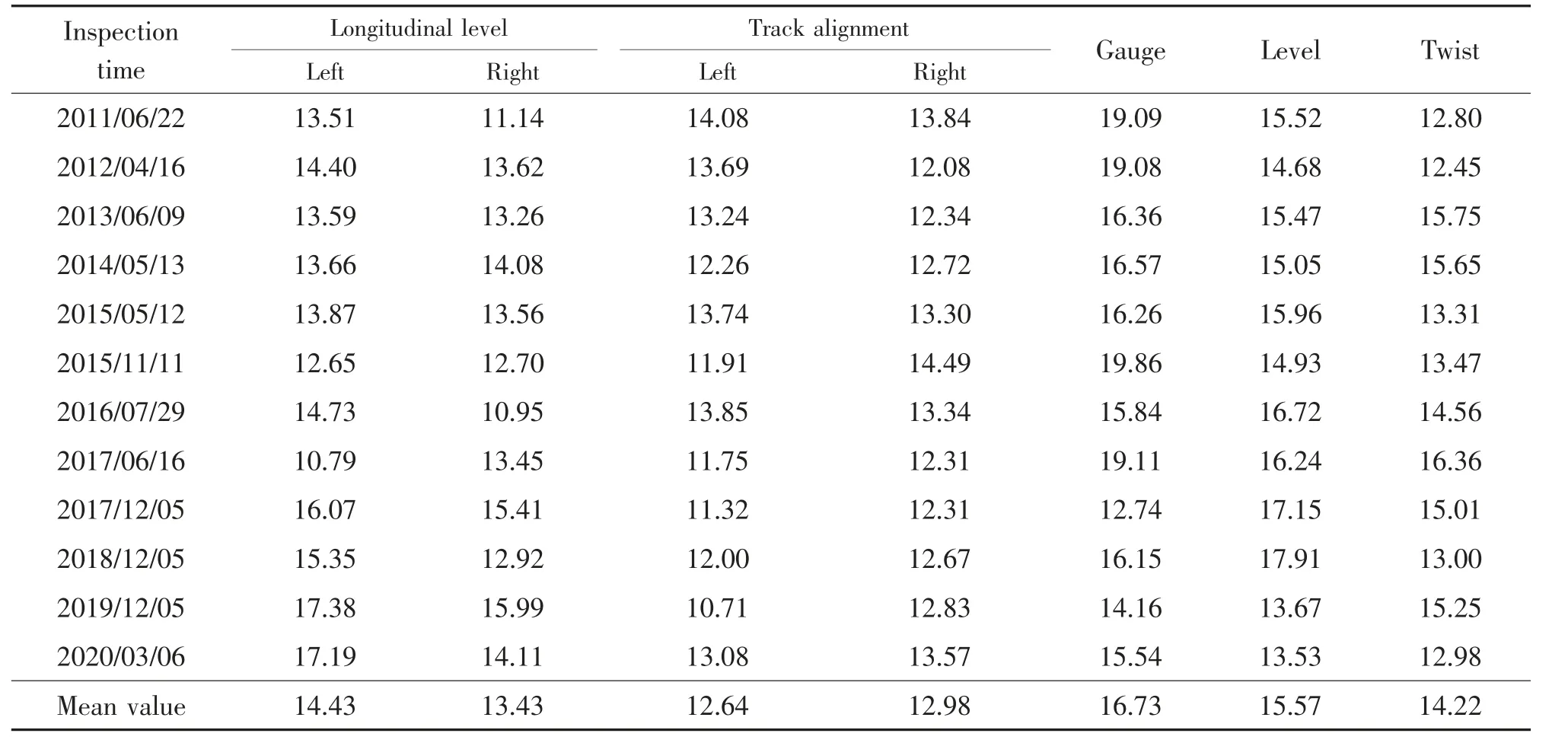
表3 历年TQI 各项分量的权重系数Tab.3 Weight coefficient of each component in TQI over years %
2 放大系数
我国高速铁路无砟轨道的平顺性管理主要依据《高速铁路无砟轨道线路维修规则》, 其中关于TQI 及单项分量的管理标准见表4, 该标准仅针对不同速度等级的线路进行分类,没有具体的分级处理方法。
与此同时, 管理人员在工务实践中通常仅对TQI 超限地段进行轨道管理, 对单项标准差超限值的关注较少,导致某些区段评价的失真。 以高低不平顺为例, 从表4 中可以看出, 对于速度等级为250~350 km/h 的线路, 当高低不平顺标准差小于0.8 时为合格,否则为超限。 实际上当高低不平顺标准差接近0.8 时, 线路不平顺状态已经恶化到一定程度,虽然尚未超限,但也不容忽视。 然而,工务管理中对这一部分的关注较少,这对于高速铁路无砟轨道的几何状态不平顺精细化管理是不利的。
文章将单项不平顺标准差的管理值分为“≤sti/ 2”、“sti/ 2~sti”、“>sti” 3 个等级,通过不同的放大系数进行计算,如图1 所示。 放大后的单项分量计算公式如下
式中:si为放大后的单项分量;sti为表4 中各单项分量的管理值;k1,k2,k3分别为放大系数(通过试算后,分别取k1=1,k2=2,k3=4)。
从式(4)和图1 可以看出,对于高低分量小于0.4 的值,该值距离超限管理值尚远,放大系数为1,仍采用现值; 对于高低分量大于0.4 但小于0.8 的值,该值虽未超限,但距离超限值较近,将该分量超过0.4 的部分进行2 倍放大,需要一定程度的关注;对于高低分量大于0.8 的值,该值已经超限,但可能由于其它分量较小,TQI 并不会超限,将该分量超过0.8 的部分进行4 倍放大, 对于该值对应的里程需要重点关注。 放大后的单项分量组成的TQI 值,在原TQI 值接近超限但尚未超限的区域也会超限,在管理人员对TQI 超限地段进行轨道管理时能够对单项分量接近超限或已超限的区域管理到位。
3 基于放大系数和不同权重组合的TQI 综合指数计算方法
针对高速铁路无砟轨道不同线路区间TQI 平均值相差较小的问题,在赋予单项分量不同权重和放大系数的基础上,还需要进一步将TQI 的值域范围扩大。最终,结合加拿大轨道单项几何参数指数[20]的计算原理,提出基于放大系数和不同权重组合的TQI 综合指数(以下简称“新TQI 值”),计算公式如下
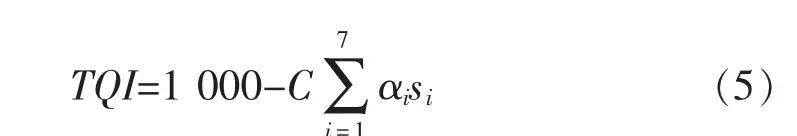
式中:αi为各单项分量的权重, 根据表3 确定;C为经验常数, 经反复试算后取C=700。 新TQI 值在0~1 000 之间变化,值越大说明线路状态越好。
采用式(5)中的计算方法,统计某无砟高速铁路2020 年3 月份的新TQI 值, 绘制成频率分布直方图,如图2 所示。
从图2 可以看出,考虑了放大系数和不同权重后,新TQI 最大值为831,最小值为241,值域范围较大。 其中新TQI 值在600 以下的单元区段数占5.4,在600~700 之间的占7.6,在700~800 之间的占82.2,在800 以上的占4.8。

图2 新TQI 值频率分布直方图Fig.2 Histogram of frequency distribution of new TQI


为了探索新TQI 值与原TQI 值的关系,图4 绘制了某无砟高速铁路2020 年3 月份的新TQI 值与原TQI 值散点图。 从图4 可以看出,新TQI 值与原TQI 值之间的相关系数r 达到-0.987 6,表明两者具有高度相关的线性关系。

图3 新TQI 值与原TQI 值的对比情况Fig.3 Comparison between new TQI and original TQI

图4 新TQI 值与原TQI 值散点图Fig.4 Scatter diagram of new TQI and original TQI
采用同样的方法,统计某无砟高速铁路历年来的新TQI 值与原TQI 值的计算结果见表5 和表6。从表5 可以看出,将新TQI 值分为4 个区间,各区间范围存在一定程度的重叠,并且两者具有高度相关的线性关系。

表5 新TQI 值与原TQI 值在各区间内的对应关系Tab.5 Corresponding relationship between new TQI and original TQI in each interval
从表6 可以看出,在2016 年以前,新TQI 值在前3 个区间内分布较为均匀;而2016 年之后,新TQI 值主要集中于700~800 之间。 如果新TQI值落在4 个区间内依次表示差、中、良、优,2016年之后,90%以上的区段为优良,仅不到10%的区段为中或者差。通过查阅线路的维修数据,发现该无砟高铁线路在2016 年进行了线路整体精调。
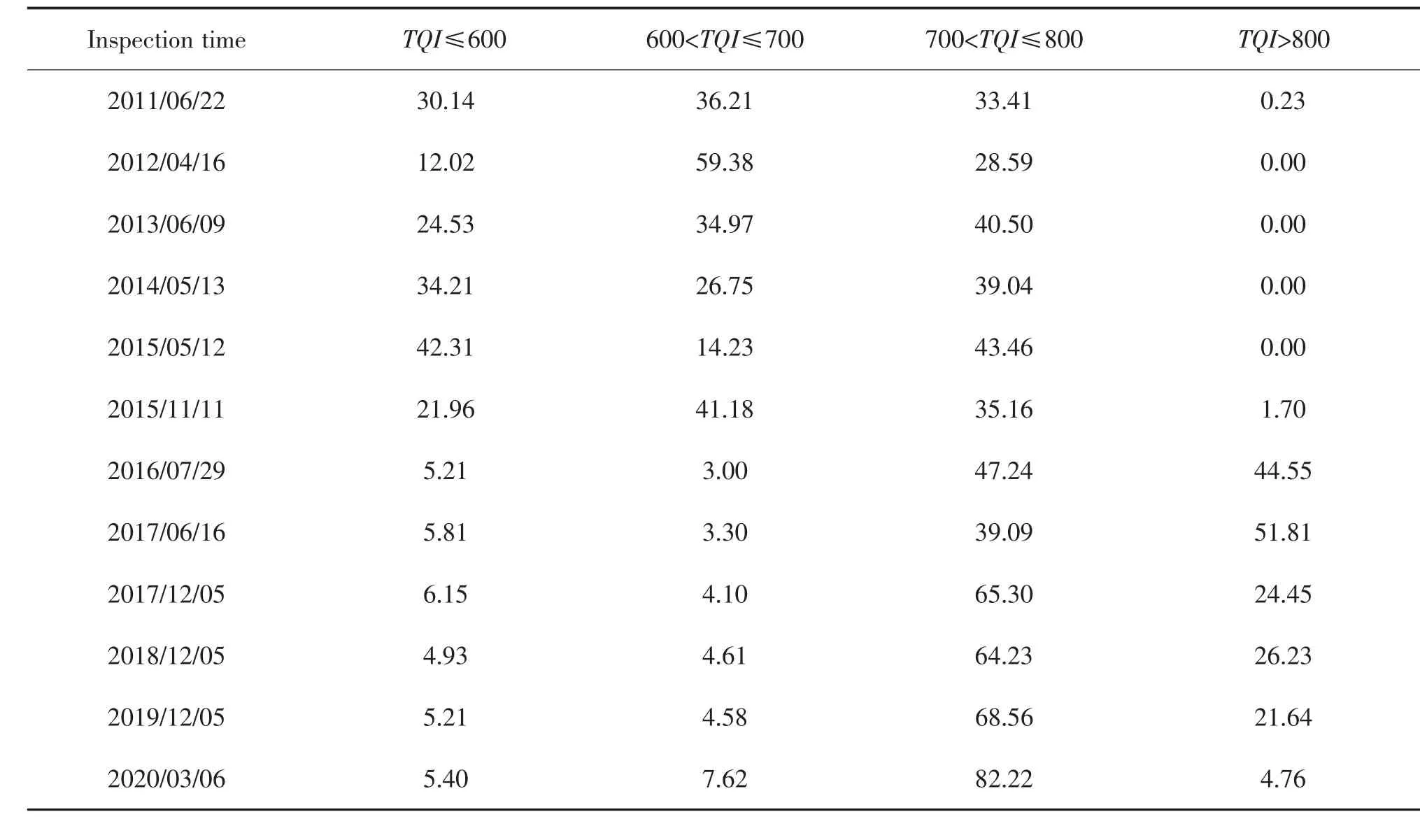
表6 新TQI 值在各区间内的百分比统计Tab.6 Percentage statistics of new TQI in each interval
4 结论
1) 对某无砟高速铁路而言,扭曲不平顺占TQI的比重是最大的; 然而轨距分量的变异系数更大,表现为轨距标准差在该线路区域上时大时小,在TQI 计算结果中需要将轨距分量突出。
2) 针对高速铁路无砟轨道不同线路间的TQI值相差很小且TQI 及单项分量的管理标准中没有具体分级处理方法的问题,提出了基于放大系数和不同权重组合的TQI 计算方法,并将最后结果分为差、 中、 良、 优4 个区间, 依次为TQI≤600、600<TQI≤700、700<TQI≤800、TQI>800, 可以对高速铁路无砟轨道线路平顺性进行更好地评估和管理。
3) 该方法在新线联调联试过程中的适应性,需要更多数据进行分析。

