基于“一题研究”教学设计

张琴兰

一、教学内容

在带领学生进行平面图形面积的复习、整理过程中能够结合学生以往学习过的长方形、正方形、三角形，以及平行四边形、图形的面积计算的相关知识经验，进行习题的合理创造开发，这样既可以帮助学生系统、高效的完成相关知识点的复习、整理，也能够进一步理清楚平面图形之间存在的脉络关系，全面激活、拓展学生的数学思维。

二、教学设计

（一）理清脉络，设计问题序列

新课标强调，不能让学生在数学学习中处于死记硬背的状态，要实现透彻理解，然后在具体引用中不断巩固深化。在实际授课中，要重视数学知识与学生实际生活经验，以及其他学科的密切联系，组织学生开展实验、操作，以及尝试等一系列活动，引导学生逐渐养成细致观察、全面分析的良好习惯，且能够引用所学知识经验来做出一些判断。同时，还要将知识的数学实质，以及具体体现了哪一数学思想揭示出来，帮助学生更快速、准确的理清各知识点之间存在的联系、区别。所以，在一题研究的教学设计，应加强对相关知识的“生长点”与“延伸点”的关注，构建出更完善的知识体系，妥善处理好局部知识、整体知识之间的关系。这樣在帮助学生优化数学知识体系的同时，也能够促使其正确认识到，很多数学知识其实是可以从不同角度来分析理解的。因此，在数学教学中，教师要将知识脉络理清楚，实现对教材的科学、合理引用。围绕一题来优化问题序列设计，通过带领学生循序渐进的分析、解决各个问题来增强课堂教学有效性，从不同层面来激发、增强学生数学学习兴趣，将一题一课的优势特点充分突显出来。且在此过程中，一定要突出本质，完善 活动经验积累。在学生学习探究过程中，应引导其真正做大学练结合，一边学习一边练习，一边练习一边思考，一边思考一边学习。

针对“平面图形面积的复习与整理”一共设计了三个活动（详细活动实施见下面的教学实施）。活动一，提出一个开放性问题，以此来引导学生动手画一画、练一练，同时进行深入思考。活动二，主要是引导学生结合活动一中活动的体验来做出深入探究，在经历了自主操作、深入体验之后积累更丰富的经验、方法，从不同层面来激活学生数学思维，使得学生可以更进一步的了解数学知识本质。另外，还分层设计了三个练习，通过这些练习来帮助学生加强巩固、提升，以此来真正做到学习、练习的密切联系，促进课堂教学有效性的显著提升。活动三，主要是引导学生对平面图形面积的计算公式进行复习、巩固，让学生在小组探究分析中对各个平面图形之间存在的联系做出深入了解，进一步完善平面图形知识网络的构建。最后，通过拓展习题的巧妙设计，来有机整合平面图形的各个知识点，对学生进行综合考察。

（二）整体推进，拓展思维

针对平面图形的面积来讲，是在不同年级段中按照不同图形，进行分门别类的学习。这一方面的知识涉及到的内容非常广，跨度也有多个年级。因此，为了帮助学生更好的把握平面图形的数学思想与本质，就要将这些知识点有机整合在一起，指导学生从中整体上给予思考与分析，以此来给学生数学思维的全面发展创造良好条件。

（三）拓展提升，优化自主构建

结合相关知识点，分层开展练习设计与编排，以此来达到巩固新知、拓展提升的目的，为数学知识体系的自主构建、完善提供有力支持。针对“平面图形面积的复习与整理”这节课来讲，主要设计了三道练习：

第一题，主要是带领学生巩固所学新知，引导学生充分认识到新知知识带来的全新思维角度与便捷，使得学生的数学思维可以得到进一步拓展。

第二题，重点引导学生做出深入探究。通过这一习题的设计，主要是为了给学生创造独立思考探究的空间，让学生获得更多时间操作的机会。通过这一思维活动的精心设计，帮助学生将新知纳入到现有的数学知识体系当中，然后通过现有知识经验的灵活引用来妥善解决这一开放性问题，以此来强化各种平面图形特征、关系的沟通。

第三题，通过这一变式习题的设计，希望可以引导学生从不同的思维角度来思考问题，以此来帮助学生学习、积累更丰富且适合自己的思考方法。且基于等积变形这类数学思维也能够将题目化难为易，以此来帮助学生不断拓展数学认知视野，给其数学核心素养的进一步发展，以及今后的数学学习奠定良好基础。

总之，通过对教材习题的合理开发、充分利用，巧妙的进行变式设计，既可以帮助学生更轻松的完成新旧知识的密切联系与巩固，也能够不断拓展其认知视野，学会举一反三，从而给其数学学习、应用能力的进一步提升创造良好条件。

三、教学实施

活动一：在一组平行线之间画出高为4，面积为20的平面图形。

（1）布置要求：要将之前学过的图形画出来。

请大家想一想要怎样画？看看谁画的种类多，谁画的准确。老师为大家准备了一些小纸片，一张纸片上画一幅图。（为学生提供三分钟的时间，然后让学生展示）

教师收集了几类作品。这些平行四边形长得好像不太一样，都符合要求吗？这样的平行四边形还可以画出几个？还有的同学画的是三角形，在画的时候是怎样想的？试着猜一猜，这样的三角形还可以画几个？可以和大家分享一下自己是怎样画的吗？还有的同学画出了梯形，请大家看一看是否符合要求，还能否画出不一样的梯形？

活动二：通过梯形的变换来加强图形之间的沟通联系。

（1）请大家对这四个梯形做出细致观察，思考一下，其上下底有什么特点？然后与同桌分享一下自己的发现。结合大家的发现，将其上底继续往右延长，会出现什么变化？最终会变成怎样的图形？

（2）通过课件演示：梯形、三角形、平行四边形与长方形的变化过程。以此来带领学生更清晰的看到动态展示变化的过程，从而做出全面了解与深入思考。

（3）结合一连串的变化思考，其中什么是始终未发生改变的？在这些等积变形过程中，有一些图形是比较特殊的。以往，大家都是分开来进行梯形、平行四边形、三角形、这四种图形的讲解，而通过今天的整合研究，是否获得了什么不一样的发现？

活动三

（1）大家已经学过哪些平面图形面积的计算？能否将不同图形的面积计算公式说出来？能否运用字母来表示？

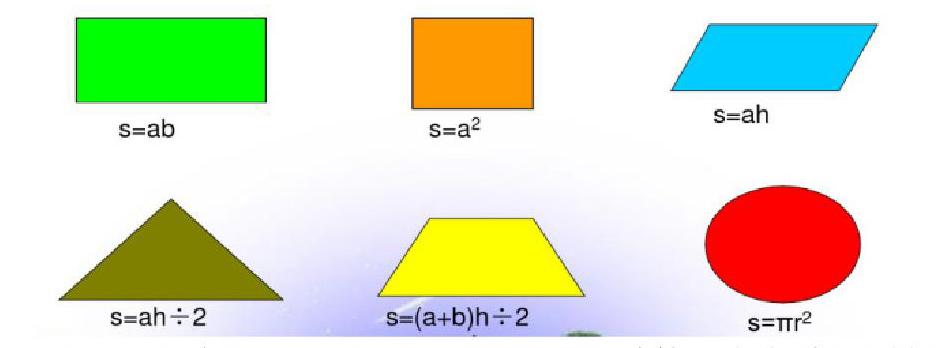
（在学生回答之后，课件展示6各平面图形及其计算公式与图形整体：长方形：面积=长×宽;正方形：面积=边长×边长;梯形：面积=（上底+下底）×高÷2;三角形：面积=底×高÷2;平行四边形：面积=底×高;圆：面积=圆周率×半径×半径）

（2）小组讨论：这六种平面图形的面积计算公式分别是怎样推导出来的？请大家每人选择一到两种喜欢的图形，然后引用学具，与小组成员一起讨论分析一下面积的推导过程。

（3）组织交流：有没有哪位同学想要与大家分享一下自己选择的图形，以及面积推导过程。（学生根据所选图形来说一说面积计算公式的推导过程，在此过程中，教师引用多媒體来同步进行展示该图形的面积公式推导过程。）

（4）完善知识网络构建：通过对这些面积公式的推导的回忆，大家有什么发现？事物与事物之间有着密切联系，且是相互沟通的。大家能否结合这些面积公式之间存在的密切联系，以网络知识结构图的方式来进行整理，以此来做到清晰呈现、便于记忆？（为各小组提供一定的独立、自由空间，让各小组展示自己在合作讨论中画出来的知识结构图。）

教师也为大家整理了一份关于平面图形面积的知识结构图，大家看一看，是否和自己的是一样的。

课堂小结：这一知识结构图就像是一棵知识树一样，长方形的面积就像是这棵树的“树根”，而正方形、平行四边形的面积则是枝干。三角形与图形面积计算是平行四边形面积枝干上的叶子。由此可见，旧知识可以发展为新知识，新知识也可以进行旧知识的转化，所以，新旧知识之间存在的密切联系是不同忽视的。

教师板书：梯形的面积计算公式对于三角形、平行四边形，以及长方形也是通用的，在此基础上，再进行面积公式互通的验证。

四、习题拓展

某地规划在一块“长方形休闲区”设计一个圆形的水池，一个底座为平行四边形的雕塑，一个占地为三角形的亭子，还有一些小径与绿化面积。请大家结合现有知识经验，以及上述要求，充分发挥想象力、创新力来进行休闲区平面图的设计，并将相关平面图形的米娜及计算出来，清晰的标注在图上。注意体现美观合理性。

五、教学总结

在设计组织“一题一课”的教学活动中，应对以下几点做出充分考虑：

一是理序：一定要实现对新课标教育理念的深入钻研、准确把握。在此基础上，实现对题目的深入剖析、研究，实现对题目相关信息的灵活引用，构建出更清晰、完整的知识体系，将题目具有的功效充分挖掘出来，也只有这样才能够真正在一题研究的教学设计中真正做到“借题发挥，题尽其用”。

二是悟本：要注重对一体求解知识的巧妙引用，通过对相关知识点的进一步梳理来构建出更完善的知识网络，促使学生在进一步优化数学知识体系构建过程中，对数学知识真正的思想、方法做出深入探究，实现对数学本质的深刻领悟，充分感受到数学知识的魅力。

三是促思：精心设计变式来促使学生不断强化对现有知识经验的应用探究，这样既可以帮助学生不断完善数学知识体系，也能够给其数学综合素养的进一步发展创造良好条件。在此背景下，学生也能够真正实现通过做一题、通一类、会一片，实现对数学知识精髓、本质的准确掌握与活学活用，给其数学思维的进一步拓展带来积极的促进作用。此外，还需要注意的是在一题研究的教学设计中，有的题目是可以从教材、练习本上找到合适的，然后直接拿到课堂上使用，但也有的题目是需要教师结合学生认知特点、教学需求来做出合理改变，或者是通过自主创造来获得的，只有这样才能够符合教学需求。

总之，小学数学课堂教学中，要促进其授课效果与效率的显著提升，从不同方面来挖掘学生各方面潜能，就要及时更新自身教育理念，对数学教材中的各类习题做出深入钻研，对教材知识内容做出合理开发，也只有这样才能够真正实现对课堂与学生共鸣之处的准确把握，才能够激发更多学生积极主动参与到各项学习探究活动当中，才能够促使学生一直保持浓厚的学习兴趣。同时，为了确保一题研究教学模式的优势特点可以得到充分发挥，真正做到小题目、大内涵，还需要联系实际，从不同层面来对这一教学模式的应用做出深入研究，探索出更完善、适合的教学策略。