考虑间歇期的飞机连杆式舱门收放机构竞争失效分析
刘敬一, 张玉刚, 庄新臣, 庞欢
(1.长安大学汽车学院, 陕西西安 710064;2.西北工业大学航空学院, 陕西西安 710072;3.清华大学机械工程学院, 北京 100091)
连杆式舱门收放机构在飞机中应用广泛,诸如起落架舱门收放机构、货舱门收放机构等。该类机构的失效会直接影响到飞机的安全性,确保该类机构的可靠运行尤为重要。本文所研究的某型飞机舱门的连杆式收放机构,存在突发型失效和退化型失效并存的现象,机构系统的实际失效是此二类失效相互竞争的结果。充分研究该机构的运行原理,结合机构的运行具备间歇期这一实际特点建立竞争失效模型,可以更为准确地对该机构可靠度的演化进行评估。
目前,在有关飞机机构的竞争失效研究方面,侯聿[1]研究了飞机起落架收放作动筒指型锁的磨损;刘成业等[2]针对某型民用飞机舱门锁结构变形现象,从接触力角度开展了失效研究。以连杆机构为例,印寅[3]分析了某型起落架的动力学特性,并对起落架机构进行了可靠性研究;郑怡[4]基于多体动力学,分析了发动机中连杆机构的动态应力,对连杆失效造成发动机的破坏性故障进行了研究。郭庆、刘晓娟等[5-6]分别研究了航空发动机的竞争失效行为,从寿命预测、可靠性评估和性能退化等不同角度对航空发动机的可靠性进行了研究。对于构件数目较多的连杆机构而言,各个构件的尺寸误差和运动副中的间隙会产生较大的累计误差,容易造成运动精度的不足,但当前有关飞机机构竞争失效的研究尚未涉及连杆类机构运动精度不足的问题。
在有关竞争失效模型的研究方面,Rafiee等[7]认为外界冲击的出现会引起退化过程退化速率的改变,并综合多种因素建立了的竞争失效模型。Qiu等[8]考虑退化过程的2个阶段建立了竞争失效模型,并基于此分析了输油管道的可靠性。Yang等[9]研究了处于竞争失效模式影响下的油气输送管道的维修保障策略。Hao等[10]对处于局部放电失效和漏气失效2种失效模式影响下的气体绝缘输电保护装置进行了研究,建立了竞争失效模型。齐佳[11]建立并用试验验证了性能退化自恢复产品的相关竞争失效模型。逯程[12]等则研究了竞争失效条件下对装备的选择性维修方法,考虑多种维修方式对处于多失效模式竞争作用下的系统进行了维修方式选择的综合优化。总的看来,现有的竞争失效模型并未考虑实际工作中“工作期”和“间歇期”相互结合的特点,需要建立新的模型。综上,本文引入间歇期因素,建立了适用于飞机机构的竞争失效模型,利用泊松过程、Archard磨损模型分别对突发型失效和退化型失效进行研究;利用所建模型,对某型飞机连杆式舱门收放机构的结构组成、工作原理和失效行为进行深入研究,结果证明所建模型能够有效地应用于该机构的竞争失效分析,同时可以推广至其他具有相同特点的机械机构系统的研究之中。
1 基本描述
间歇期是区别于工作期的机构工作时间段,在此时间内机构面临不同的环境特点,机构自身的性能退化速率也会发生变化。飞机机构通常处于两类失效模式相互竞争的影响之下,一类为退化失效(例如机械轴的磨损、部件的老化),一类为因外界冲击(例如意外的过大的工作载荷、振动冲击引起的载荷等)导致的突发失效。对于突发失效,使用极限冲击模型描述,即一旦有外界冲击超过了系统的可承受量值,则发生突发失效;对于退化失效,使用考虑随机参数的通用路径模型描述,当退化量累计至一定量的时候,系统发生退化失效。考虑间歇期的系统竞争失效过程如图1所示。
图1时间轴中实线部分表示机构的工作期。当系统处于工作期的时候,退化量在较为快速地增加,同时工作期期间会有一定的概率出现外界冲击(例如图中T1时间段内的W1和W2),也就是说在工作期期间,系统会有一定的概率发生失效。每一次工作期的时长定义为T1,它的取值可取一个恒定值或随机量值。图1时间轴的虚线部分表示机构的间歇期,间歇期的意义为在此期间系统停止工作。处于间歇状态系统的退化量因系统的“间歇”而增速减缓,同时“间歇”状态的系统不会受到外界冲击(例如图中T2时间段并没有任何外界冲击出现)。每一次间歇期的时长定义为T2,其可取一个恒定值或随机量值。相邻的一个工作期和一个间歇期定义为一次工作循环(图中T1时间段和T2时间段即可组合成一次工作循环),系统的寿命就是由若干个连续不断的工作循环组成。
2 建模过程
2.1 突发失效建模
基于极限冲击模型对突发失效进行描述,即当某次外界冲击的量值大于系统的阈值之时,系统发生突发失效,因而系统在外界冲击影响下的生存函数表示
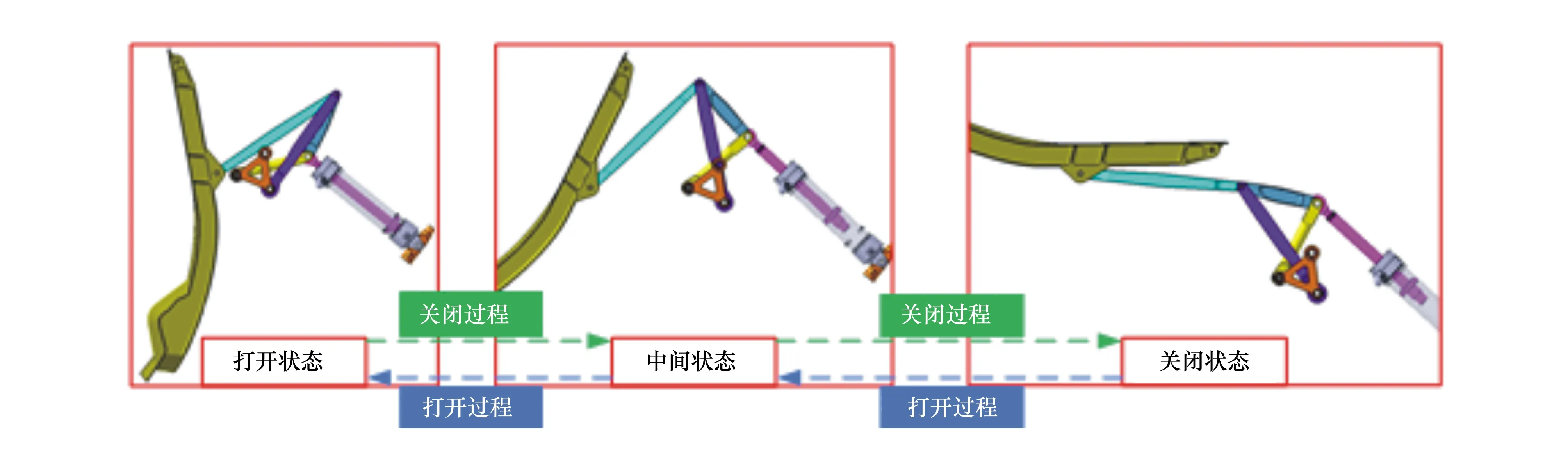
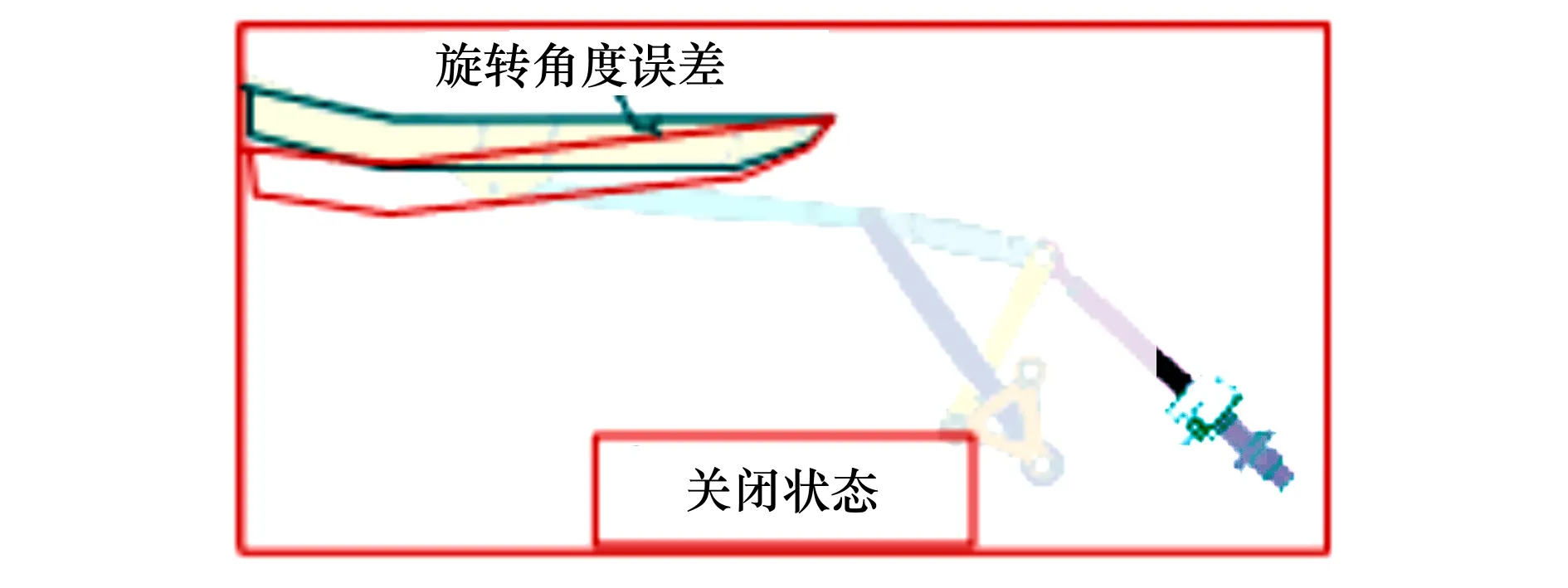
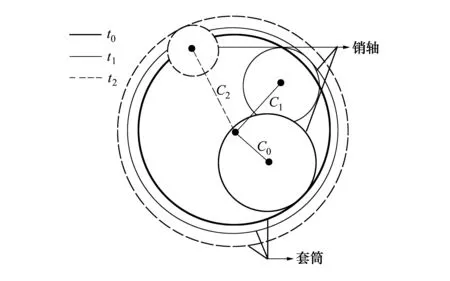
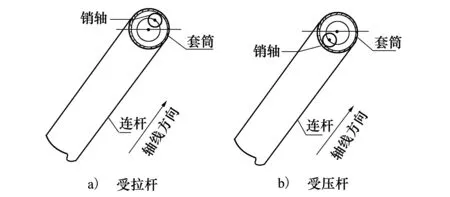
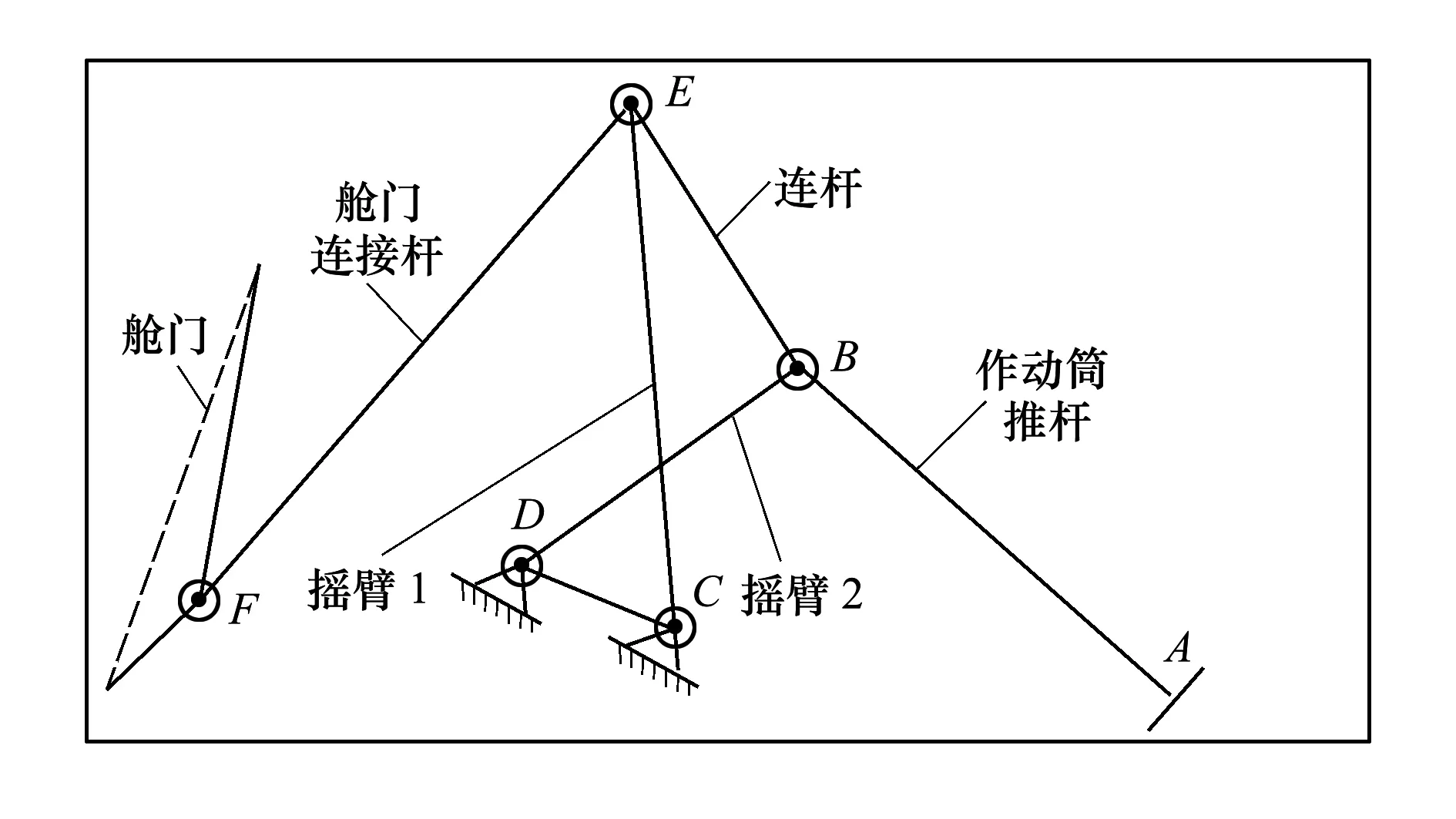
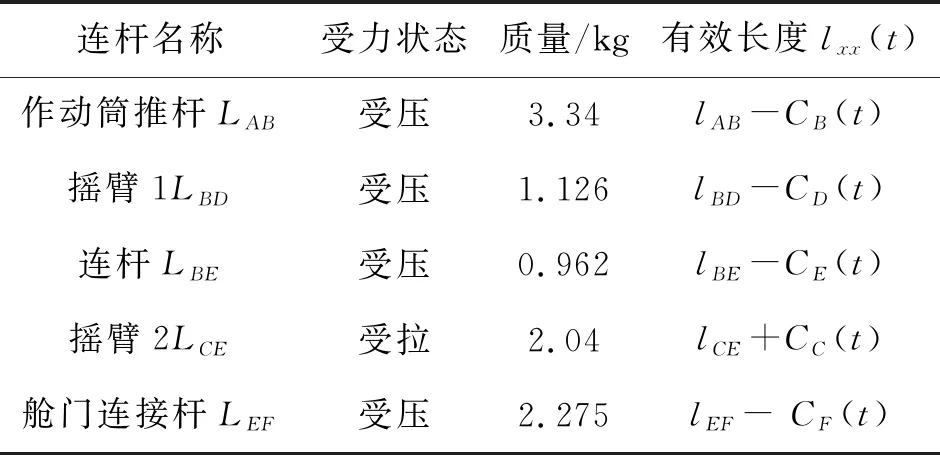
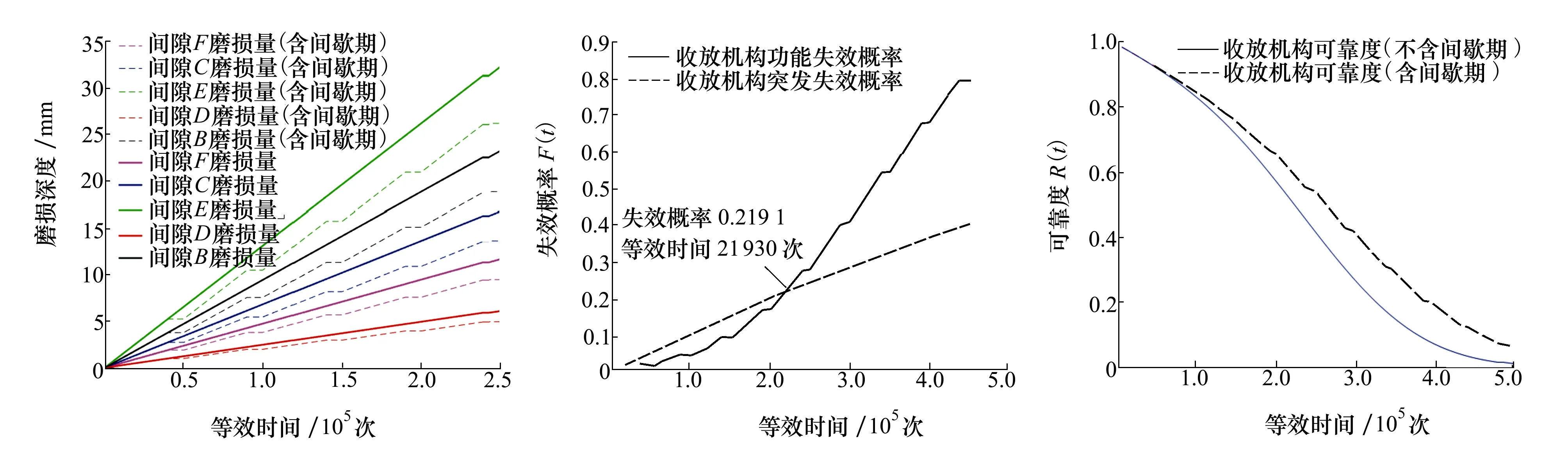
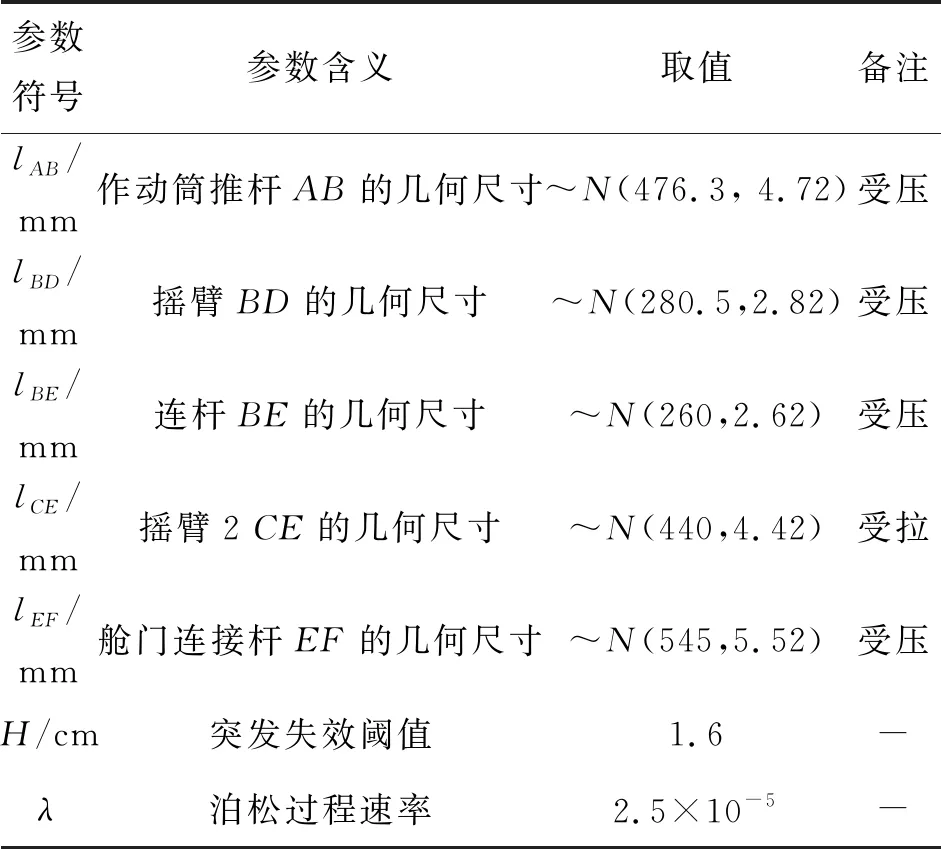
P(Wi (1) 式中:Wi为在时间ti所发生的外界冲击的大小;H是系统突发失效阈值,代表抵御外界冲击的能力。考虑一种特殊情况,如果外界冲击和系统阈值皆是符合正态分布的随机变量,上述生存函数表达式变为 (2) RH(t)=P({W1 (3) 式中:n表示工作循环的次数;T1和T2分别表示一次工作期和间歇期的持续时长。当n取固定值的时候,公式(3)中的表达式(Ⅰ)的取值会随着t而发生变化,这是因为工作期期间系统会受到外界随机冲击的影响,有可能发生突发失效,具体的概率值会随着时间发生变化;而表达式(Ⅱ)则会保持定值,这是因为间歇期并未有外界冲击发生,系统的生存概率等于上一个工作期最后时刻的生存概率。 退化量会在工作期期间随着时间而累积,因系统在间歇期未处于使用状态,故而退化量也保持定值。总的退化量Xs(t)包括因系统使用而产生的无法避免量X(t),我们称之为“纯退化”,以及因外界冲击导致的退化量增加S(t),我们称之为“额外退化”。在退化轨迹模型中,纯退化可以表示为X(t)=φ+γt,类似的,当考虑间歇期的时候纯退化进一步表示为 (4) 式中:φ为退化量的初值;γ1和γ2分别表示工作期和间歇期退化量的增加速率,三者一般是符合特定分布的随机变量。而因外界冲击所导致的额外退化可表示为: (5) 式中,N(t)是一计数过程,表示截止时刻t所发生的冲击的次数,使用速率为λ泊松过程来描述。综合上述两表达式,系统总的退化量表示为 (6) 如果系统不发生退化失效,则要求总的退化量不超过系统的许用阈值,此时的生存概率表示为 (7) 基于卷积,上述表达式进一步推导为 RX(x,t)= (8) 图2为该机构的收放过程示意图。机构可以划分为作动筒、连杆机构和舱门三大部分。作动筒为动力源组件为整个机构提供动力;连杆机构承担连接和传动的作用;舱门属于输出组件,在动力源和连杆的带动之下,实现打开和关闭状态的机构功能。该收放机构的功能要求在既定的时间内完成舱门的打开和关闭动作,由于作动筒性能退化和运动副间隙演化,导致该机构存在2个失效模式: 图2 连杆式舱门收放机构功能示意 失效模式1:作动筒堵塞导致的驱动力下降。作动筒失效的最主要原因之一是因液压油中异物导致的阻塞[13],进而导致作动筒可输出液压力下降,从而造成机构的失效。根据文献[14]可知,导致堵塞的异物来源可能是外界环境带入,也可能是由于作动筒筒壁和活塞杆之间的摩擦造成,这个过程可以用冲击模型来描述。图3为该失效模式示意图,属于突发失效; 图3 机构失效模式1 失效模式2:舱门关闭不到位。舱门是由作动筒驱动一系列的连杆运动达到关闭位置,只有达到满足要求的既定位置,舱门的关闭功能才可视为完成。但由于随机性和磨损的存在,随着使用次数和时间的延长,运动副的间隙会增大,进而有可能导致舱门无法关闭到位,当舱门的实际位置的转角和要求转角之间的误差超过一定程度的时候,就可视为功能无法完成。图4为该失效模式示意图,属于可退化的功能失效。 图4 机构失效模式2 3.2.1 突发型失效建模 导致作动筒堵塞异物尺寸的大小和出现时间都是随机的,可以把异物看作是量值和到来时间均不确定的外界冲击[14];只有达到一定尺寸的异物才会导致堵塞的发生。以Wi表示出现在液压油中异物的尺寸大小,H表示能够造成作动筒堵塞的临界尺寸值,该机构不发生突发失效的概率表示为: P(Wi (11) 式中,Wi是独立同分布(independent identically distributed)的变量,表示每次出现异物的随机尺寸值。使用泊松过程表示异物的随机出现时刻,综上,机构不发生突发失效的概率表示为 式中:N(t)表示泊松过程,用于衡量异物出现时刻的不确定性;λ为泊松过程的速率,表示异物出现的频繁程度,速率越大则出现异物的频率越高。不发生突发失效要求没有异物出现(即式中i取值为0)或出现的异物尺寸皆小于阈值H。 3.2.2 退化型失效建模 1) 连杆有效长度的表示 图5为连杆机构两杆件之间的铰链式运动副间隙随磨损而变化的简化示意图。实线、点划线和虚线分别表示初始时刻t0、中间时刻t1和最终状态t23个时间点销轴和套筒的尺寸变化(为了示意图的展示效果,尺寸进行了相应的放大),随着时间的演化,销轴和套筒因磨损发生了尺寸的改变,运动副间隙C0,C1和C2也逐渐增大。 图5 铰链式运动副间隙增大示意图 根据等效长度理论[15],机构连杆参与运动的等效长度由连杆本身尺寸长度、间隙尺寸和连杆所受拉压状态共同决定。等效杆长理论可简单表述为,参与机构运动传递的连杆等效长度等于连杆的实际长度加上(减去)间隙长度,表示为l′=l±C=l±(R1-R2),其中l为连杆的实际几何长度,l′为连杆参与运动传递的有效长度,C为间隙的尺寸,R1和R2分别表示销轴和套筒的半径。 如图6所示,当连杆处于受拉状态的时候,实际参与运动传递的长度会因间隙的存在而增大,有效长度表示为l+C,类似地,当连杆受压时,有效长度会因间隙的存在而减小,表示为l-C。 图6 连杆有效长度示意图 2) 运动副磨损及间隙演化建模 连杆机构铰链磨损是影响传动精度的重要因素,Archard模型[16],可以对磨损体积、滑动速度、垂直载荷以及材料硬度等参数进行解释,该模型已经得到了广泛的认可和应用。Archard磨损模型的计算公式表示为: (13) 式中:h表示磨损深度,当考虑均匀磨损的时候h等同于间隙C的变化量;s为相对滑移距离,k为无量纲的磨损系数,H为较软材料的硬度,p为接触应力,E为材料相应的杨氏模量。接触应力的大小可以根据赫兹接触理论计算求得,即 (14) 式中:F为单位长度的载荷;R1和R2为销轴和衬套的半径;υ为材料的泊松比。 相对滑移距离可以根据几何关系推导得到,即 (15) 式中:φ为一个运动周中销轴和衬套的相对转角;n为运动的周期数。 综合上述各表达式,磨损的深度可以计算为 (16) 式中:p(t)和ω(t)分别为接触应力和转动角度随时间的函数,可以通过机构的动力学分析得到。根据有效长度理论,间隙的演化使得连杆参与运动的有效长度发生改变。 3)机构功能失效建模研究功能失效的表现形式为“舱门无法关闭到位”,选取舱门从打开位置到关闭位置时候所转过的角度作为功能表征量,根据舱门工作要求,满足规定的旋转角度为A0=120°。为了提高计算效率,使用一阶响应面构造舱门的功能表征函数,构造步骤如下: step1 依据运动原理搭建参数化机构动力学仿真模型; step2 按照各输入参数的分布(见表1~3)进行拉丁超立方抽样,将抽样值代入仿真模型,得到成组的输入输出; step3 利用step2中得到的结果进行响应面的构造并进行精度验证。 构造得到的连杆式舱门收放机构功能表征量的响应面函数为: 式中:A(t)为舱门的关闭角度;l(t)表示间隙的退化影响连杆的有效长度。当舱门实际旋转的角度A(t)和要求角度A0的偏差超过许用偏差δ的时候,舱门发生功能退化失效。因此,舱门的功能满足要求即不发生功能退化失效的公式表达为: RF(t)=P(|A(t)-A0|<δ) (18) 式中:A0为理想状态舱门关闭时所旋转的角度;A(t)为舱门实际所旋转的角度,其具体的取值由功能表征函数计算决定;δ为许用误差。 3.2.3 机构可靠度及其演化规律 若要该连杆式收放机构不发生失效,则需突发失效和功能退化失效都不能发生,综合公式(12)和公式(18),推导得到机构的整体可靠度为 特殊的,若舱门的实际旋转角度A(t)服从正态分布 ,上述表达式进一步推导为: 图7为该连杆收放机构的简化示意图,结合舱门关闭状态各个连杆的拉压状态,各连杆的有效长度如表1所示。连杆式舱门收放机构并非总处于运动过程之中,而是会有一段时间的间歇状态。由于相对运动的停止,处于间歇时的连杆式舱门收放机构不会发生进一步的磨损。结合实际的工况,该连杆式舱门收放机构每有40 000次开闭(即工作状态的等效时长)就会有10 000次等效时长(即间歇状态的等效时长)的间歇状态,当机构处于间歇状态时,各个运动副的磨损不再随时间增加。根据公式(13)~(16),可以计算得到连杆式舱门收放机构各铰链的磨损规律,参数的含义和取值如表2所示。 图7 连杆式舱门收放机构简化示意图 表1 舱门收放机构连杆状态 表2 舱门收放机构磨损相关参数 图8为各个铰链间隙磨损量的演化示意图。图中纵坐标为磨损深度,横坐标为使用舱门收放机构的开闭次数所表示的等效时间。 图8 各处间隙磨损量演化示意图 图9 失效概率演化示意图 图10 连杆式舱门收放机构可靠度演化示意图 将表3参数带入公式(12)~(20),可以计算得到该连杆式舱门收放机构各失效模式的失效概率(见图9)和系统可靠度及其演化规律(见图10)。从图9看出,等效工作时间为21 930次时,2种模式的失效概率相同,而不考虑间歇期情况下2种模式失效概率相同时对应的等效工作时间约提早至2 000次。从图10可以看出,考虑间歇期后的收放机构其退化速率降低,可靠度演化速率随之减缓。在等效工作时间为21 930次时,相对应的可靠度约相差20%。 表3 连杆式舱门收放机构参数取值 本文建立了考虑间歇期的竞争失效模型,并以某型飞机连杆式舱门收放机构为研究对象,分析了其可靠度演化规律。连杆式收放机构处于突发失效(因作动筒突然堵塞导致)和功能退化失效(因运动副间隙演化导致的运动精度不足)2种失效模式的竞争作用之下,基于本文研究,做出如下结论和展望: 1) 机构铰链磨损并非直接导致机构失效,而是产生的误差通过功能表征函数进一步传递至功能表征量,引起旋转角度不符合要求引起功能失效; 2) 间歇期的存在改变了各个铰链间隙的磨损过程,使得2种模式失效概率相等所对应的等效时间由约2 000次延长至21 930次。在此时刻后,功能失效成为舱门收放机构的主要失效模式,需在维护保养工作中着重关注; 3) 间歇期使得机构可靠度退化减缓,在等效时间为21 930次时,减缓程度约20%; 4) 本文所建考虑间歇期的竞争失效模型可推广至其他具有间歇期特征的系统可靠性分析中,例如运载车辆传动系统、电脑存储系统等。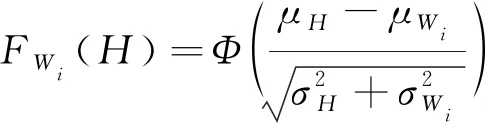
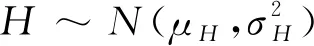
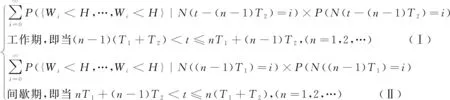
2.2 退化失效建模
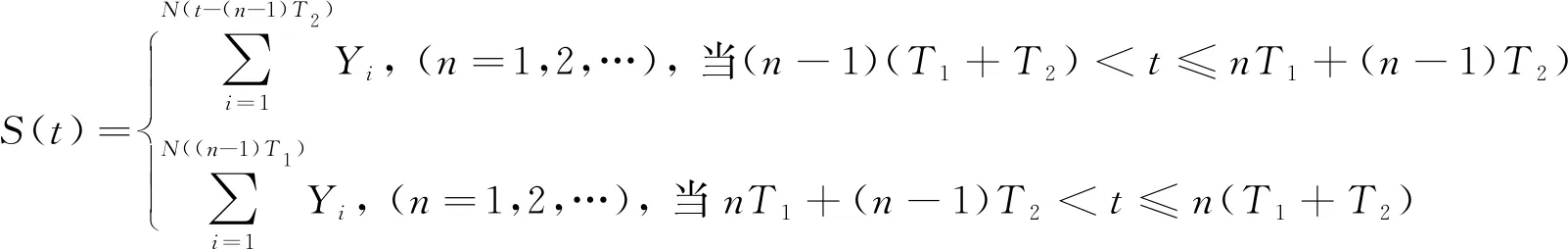

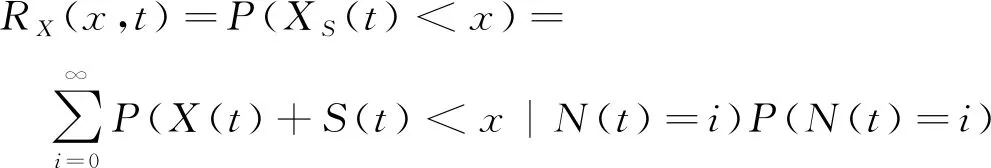
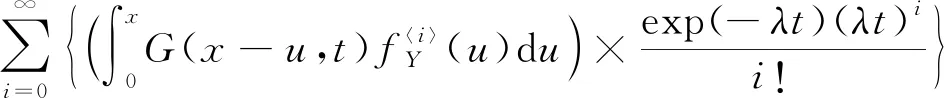

2.3 考虑间歇期的竞争失效系统可靠性及其演化建模
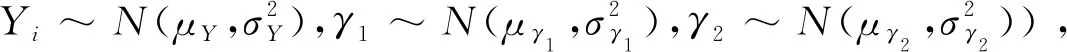
3 某型飞机连杆式舱门收放机构竞争失效研究
3.1 机构工作原理及失效模式

3.2 考虑间歇期的连杆式舱门收放机构竞争失效建模
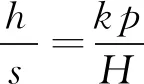
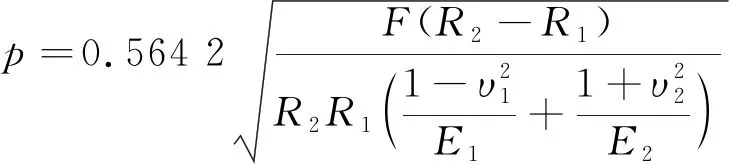
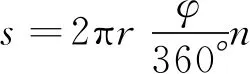
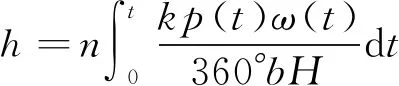
3.3 计算结果

4 结 论

