一种预制破片初速修正计算方法

崔金雷，侯俊亮，肖辉朗，王修益，曲利峰，何小旭

(1. 四川航天系统工程研究所，四川 成都 610100; 2. 四川航天电子设备研究所，四川 成都 610100;3. 陆军装备部驻成都第三军代室，四川 成都 610000)

0 引 言

破片是杀爆战斗部的主要毁伤元，破片的特征参数有破片质量、速度和飞散角等。破片的空间飞散特性决定破片是否作用于目标，而速度则决定破片能否对目标产生一定程度的杀伤。作为战斗部杀伤威力的重要参数，破片速度的准确计算对战斗部威力的评估具有相当重要的意义。

许多学者以经典的能量守恒方程为基础提出了破片驱动理论，如[1]：

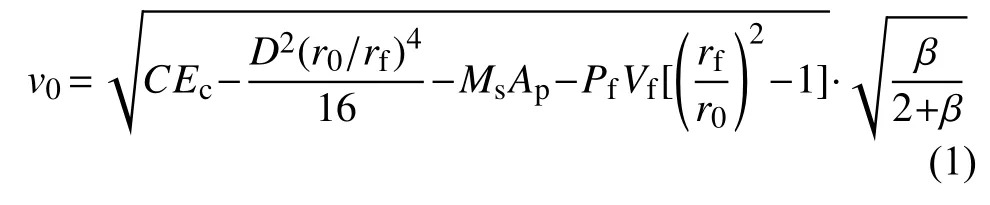
式中：C——装药质量；

Ec——装药能量密度；

D——装药爆速；

r0——装药初始半径；

rf——壳体破裂半径；

Ms——壳体质量；

Ap——其断裂比能；

Pf——壳体破裂时爆轰产物压力；

Vf——壳体破裂时爆轰产物的体积；

β=C/M，M——被驱动物质量。

弹药工程专业学者通过对以上公式实用改进获得了诸多解析公式，如最著名、应用最广的Gurney公式[2]：

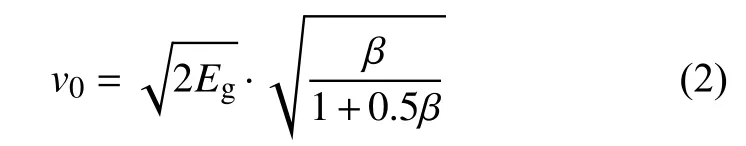
其中Eg为Gurney能。式中只考虑了装药质量、性能和被驱动质量的影响，获得的往往是更符合自然破片驱动的极限速度。应用计算不同结构的战斗部破片初速时，其精度越来越不能满足威力评估的需要。尤其是对预制破片战斗部破片初速计算时，由于内衬破裂和预制破片排布间隙的存在，爆轰产物提前泄露，计算与试验结果有较大误差，见表1。

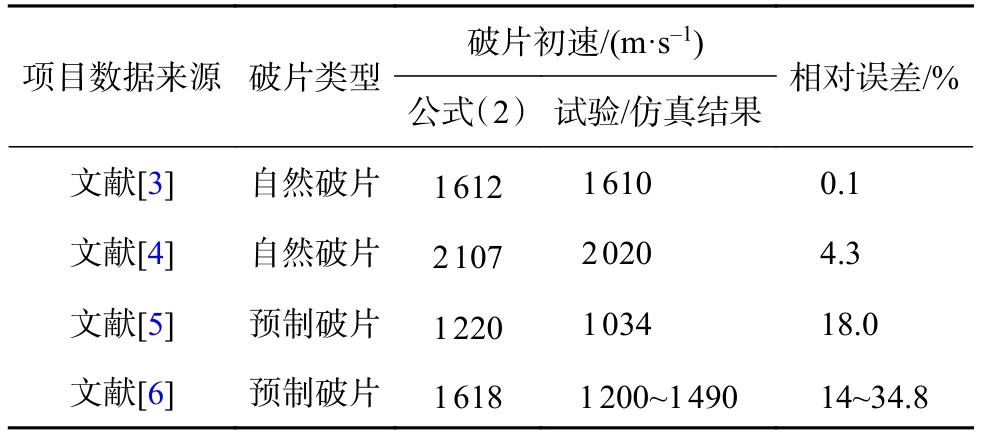
表1 经典公式计算与试验结果对比

陈兴旺等基于 Gurney 假定和相邻层颗粒之间力和力的波动量等概率传递假定，忽略排列方式引起的孔隙率变化，建立了多层破片初速场计算，其研究过程中忽略了孔隙率的影响[7]。随着计算机技术的发展，数值计算逐渐成为研究破片驱动和飞散的重要手段，苗春壮等利用三维有限元软件ANSYS/LS-DYNA对不同形状预控破片驱动过程进行了数值计算，获得了破片初速与破片形状的影响规律[8]。凌琦采用数值计算方法对定向破片的驱动过程进行了仿真，获得了破片加载过程、初速和空间分布情况[9]。

本文通过理论和量纲分析，对影响破片初速的内衬材料特性、破片形状、破片尺寸等与爆轰产物泄漏相关的参数进行了分析，采用数值计算和试验相结合的方法对不同工况预制破片战斗部的爆炸驱动过程进行了研究，以Gurney公式为基础构建出考虑爆轰气体泄漏因子的预制破片初速修正模型。该公式可为预制破片初速准确计算和战斗部毁伤评估提供参考依据。

1 理论模型

在Gurney公式基础上，本文针对柱形战斗部提出一种预制破片初速修正计算模型，其他外形战斗部可采取轴向分段近似参考计算：

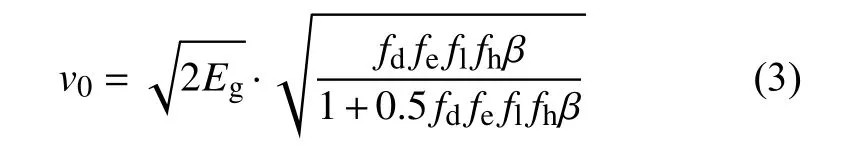
式中：fd——起爆方式修正系数；

fe——端面效应修正系数；

fl——气体泄露系数；

fh——爆轰产物密度及速度分布修正系数。

有些学者对其中的系数已经进行了修正，如蒋建伟、冯顺山等对起爆方式对破片的影响进行了试验修正拟合出了单端起爆、两端起爆和轴线起爆方式下的fd表达式[10]，Charron对端面效应进行了大量试验研究，给出了fe的表达式[11]。fh系数的研究需要高精尖的仪器设备和大量的试验经费支撑，本文将研究重点着眼于fl，即战斗部破裂造成的气体泄露对破片驱动的影响规律，研究内容包括不同的预制破片类型和尺寸，不同的内衬材料等。

气体泄露系数为纯数，经分析形成fl的函数关系如下：

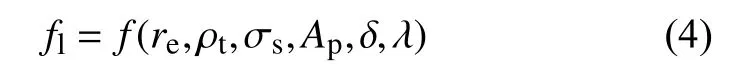
式中：re——装药半径；

ρt——内衬密度；

σs——内衬强度；

Ap——内衬断裂比能；

δ——内衬厚度；

λ——破片尺寸。

函数中有6个独立的有量纲物理量，选择为re、ρt、σs为基本量，根据Π定理，可组成3个无量纲组合，可得到气体泄露系数的相似准数。

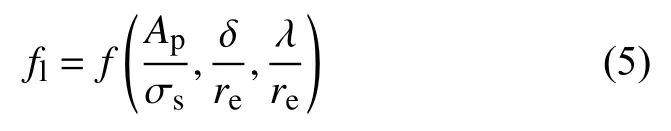
假定内衬破裂半径仅仅与内衬材料相关，忽略厚度的影响。以此为基础，式（5）可简化为：

令x1=Ap/σs，x2=λ/re，从式（6）可见，x1表征材料延展性，数值越小延展性越好，爆轰产物对破片的加速就越充分；而x2则表征破片周向排布情况，数值越小排布越紧密爆轰产物泄漏情况越轻微，破片获得的能量也越多。

2 数值计算

2.1 计算模型

选取柱形战斗部为研究目标，利用AUTODYN-3D对三种内衬材料的预制破片战斗部作用过程进行数值模拟，以获得不同形状、不同尺寸的预制破片在爆轰产物驱动下的初速规律。为气体泄露系数fl的数值拟合提供数据支撑。

柱形战斗部一般由主装药、前后端板、蒙皮、内衬、预制破片及灌封胶等组成，数值模拟模型示意见图1。主装药为Ф36 mm的TNT药柱，前后端板均为5 mm厚的45#钢板，蒙皮为铝或非金属，内衬为1100铝、45#钢或聚氨酯泡沫材料，灌封胶选用nylon材料，而预制破片选用30CrMnSi材料，破片特征尺寸选取2～6 mm，战斗部装药由前端面中心点起爆。

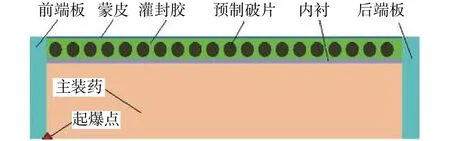
图1 数值计算模型

根据几何缩比，数值模拟模型中蒙皮厚度小于0.5 mm。考虑到计算蒙皮厚度方向尺寸小，网格划分时将导致计算规模的大幅度增加，计算中将蒙皮转化为内衬一并建模以提高效率。考虑到结构的对称性，计算模型采用1/4模型。

建立网格模型过程中，综合考虑计算精度和效率，尺寸规定如下：模拟主装药Euler区轴向径向网格尺寸1 mm，前后端板网格尺寸1.66 mm，破片特征尺寸(直径、边长)方向网格数6，内衬厚度方向网格数7，轴向网格数240。

空气域采用Euler算法，除对称面外，各边界设置flow_out边界条件，实现Euler场边界物质和能量的流出。灌封胶及炸药则采用填充方式fill到空气域中，炸药瞬态爆轰后在空气域中流动。多物质Euler场及边界条件如图2所示。

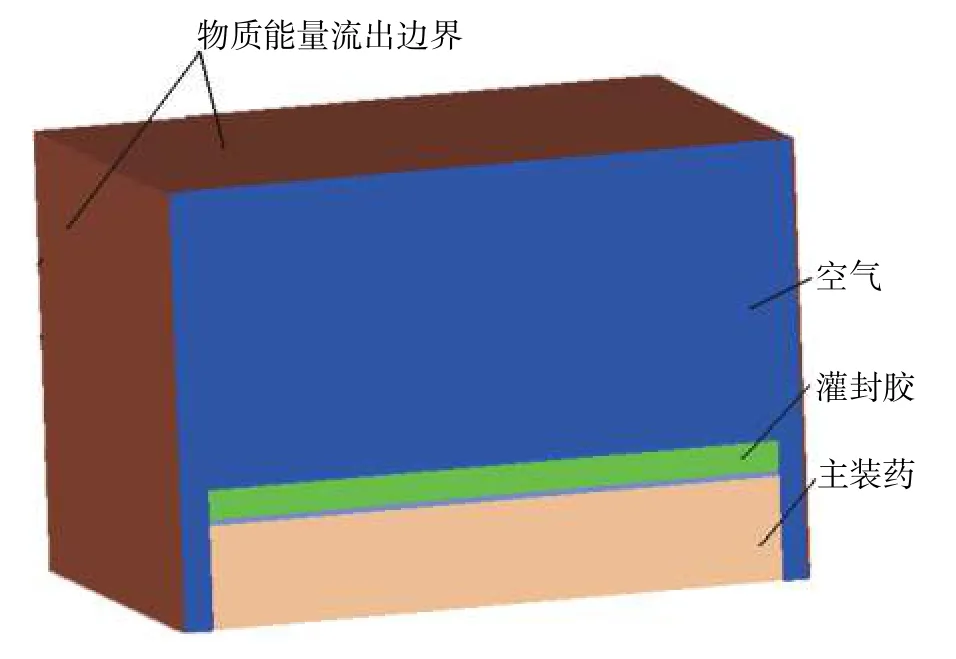
图2 多物质填充及Euler边界条件

2.2 材料模型

空气采用 IDEALGAS状态方程 (equation of state，EOS)描述，方程为：

式中：P0——空气压力；

e——单位体积空气热力学能；

γ——多方指数；

Pshift——压力偏移量。

对于空气模型： γ=1.4，ρ取 0.001225 g/cm3，e在mm/mg/ms单位制下取2.068×105。

TNT炸药采用Jones-Wilkins-Lee状态方程，方程及相关参数如下：

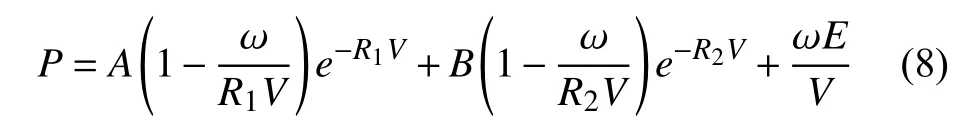
其中，P为爆轰压力；V为相对体积；E为单位体积爆轰产物热力学能，其余为材料参数。

对于破片、前后端板、灌封胶和内衬，选用冲击波速度和材料质点速度相关的冲击波状态方程(shock)，即 Mie-Gruneisen 方程；

Mie-Gruneisen方程为：

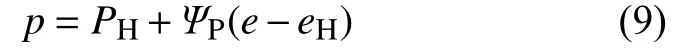
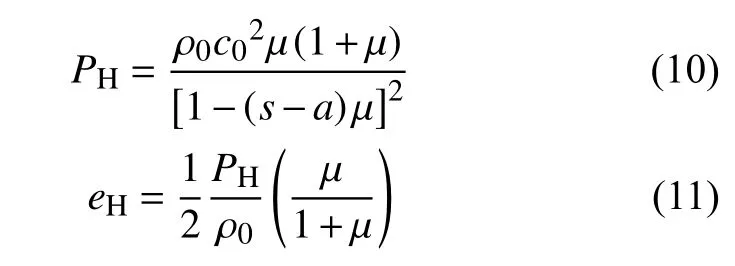
其中，µ = ρ/ρ0−1，ρ0为材料初始密度；ρ为材料密度；c0为材料声速。

质点速度方程为：

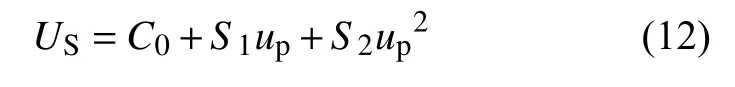
其中，up为冲击波速度；C0、S1和S2为试验常数。

破片和内衬强度模型选取Johnson-cook弹塑性方程，该模型一般用于描述材料在大应变、高应变率下的强度状态，非常适合材料在高速冲击、爆炸载荷环境中的应力计算，屈服强度方程为：

TH——对比温度；

A——材料低应变时的屈服强度；

B和n——表征材料应变硬化的常数；

C和m——试验常数。

其中TH=(T−Tr)/(Tm−Tr)，T为材料温度，Tm为材料熔点，Tr为环境室温。

聚氨酯泡沫由无强度材料描述，在冲击波作用时瞬间破裂。材料的Gruneisen状态方程参数见表2，Johnson-cook强度模型参数见表3。

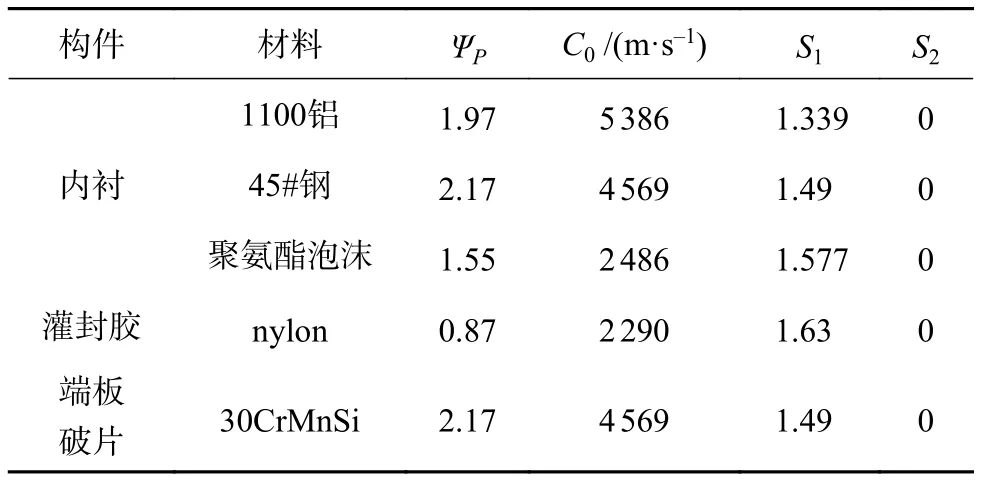
表2 Gruneisen状态方程参数

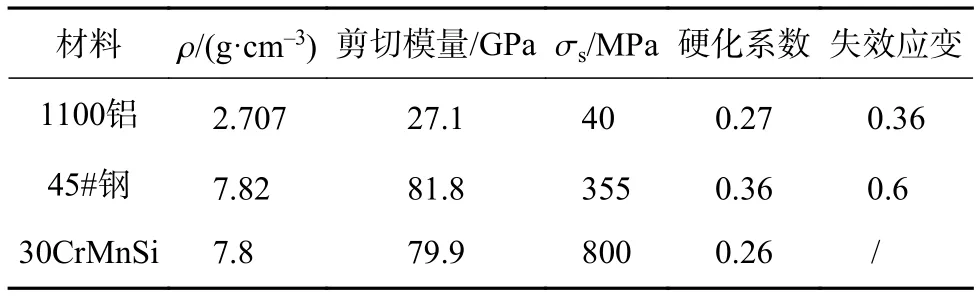
表3 Johnson-cook强度模型材料参数

2.3 结果及分析

对建立的数值模拟模型进行计算，获得了不同算例的破片初速，从破片初速轴向分布来看，战斗部两端速度较低，尤其是前端面，这与Charron、冯顺山和蒋建伟等对破片轴向速度分布的研究结果一致[2,8]。图3为铝内衬典型工况典型时刻的破片速度分布云图。

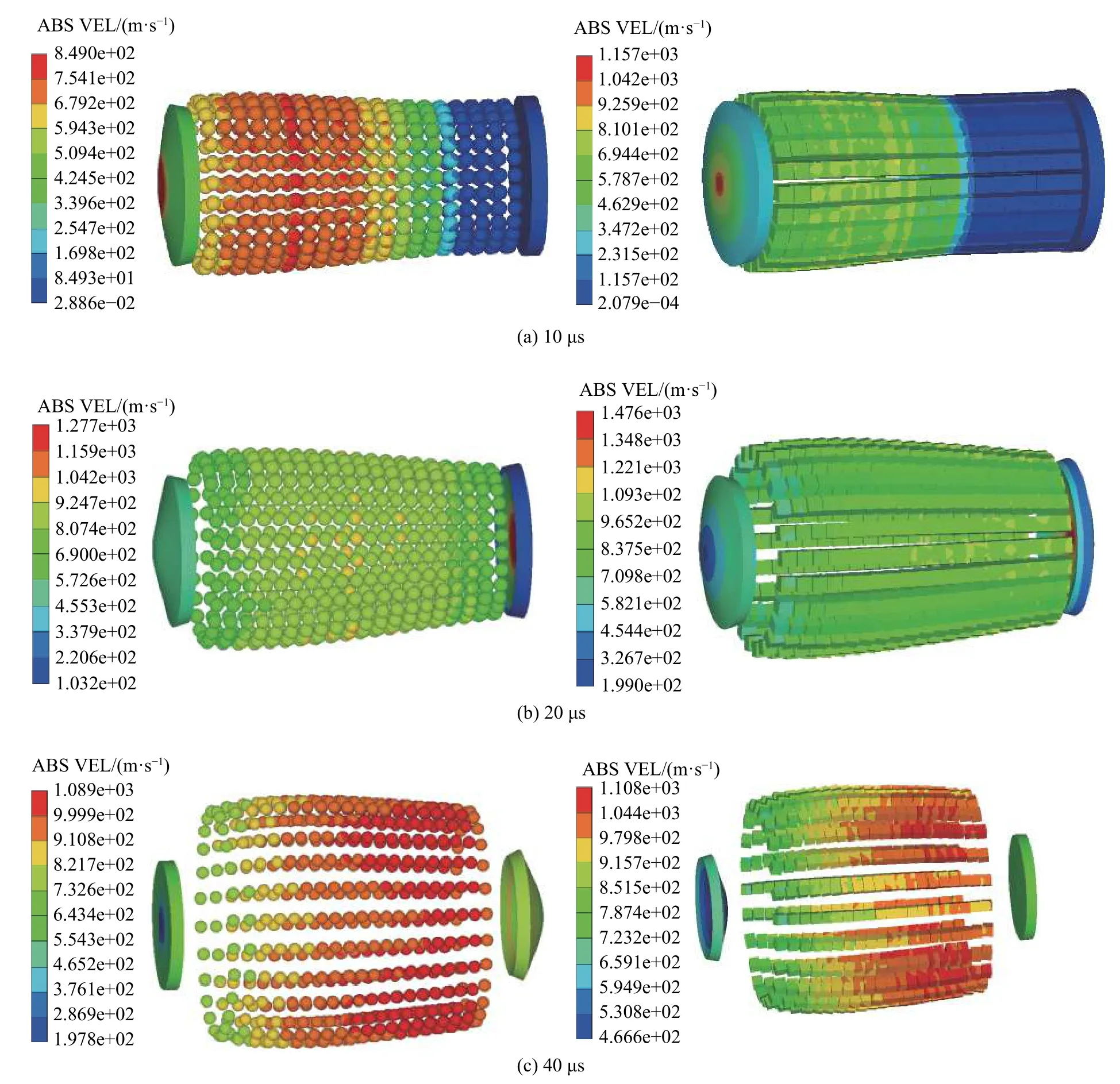
图3 尺寸5 mm的球形和立方体破片典型时刻的速度云图

从不同预制破片在典型时刻的飞散情况可以看出，随着爆轰波轴向传播，战斗部呈喇叭状膨胀，最后形成前端直径偏小的鼓状，破片逐渐分离径向飞散。边长5 mm的立方体破片算例中，不同破片的速度-时间曲线如图4所示。

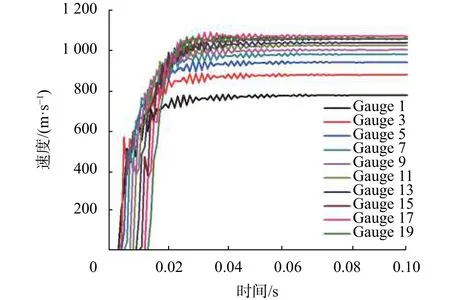
图4 边长5 mm的立方体破片算例中轴向破片速度曲线

可见，战斗部起爆40 µs后，破片速度已达到最大值，继续计算只是破片在空气中无阻尼飞行，对初速计算结果已无影响。本文研究的是内衬材料，破片类型、尺寸对破片初速的影响规律，因此需排除端面效应、起爆方式等影响因素。根据破片初速轴向分布特点，取战斗部轴向60～75 mm范围内破片作重点研究，取其中破片的最高速度为初速数据。

爆轰产物驱动下，不同内衬材料的破裂半径不同。根据能量守恒理论，破裂半径越大，爆轰产物泄露的能量越小，破片也就获得更多动能，从破片初速曲线看内衬约在15～25 µs时破裂。以直径为2 mm的球形破片不同内衬材料的工况为例，对20 µs时刻破片上的压力值进行对比，计算结果见图5。

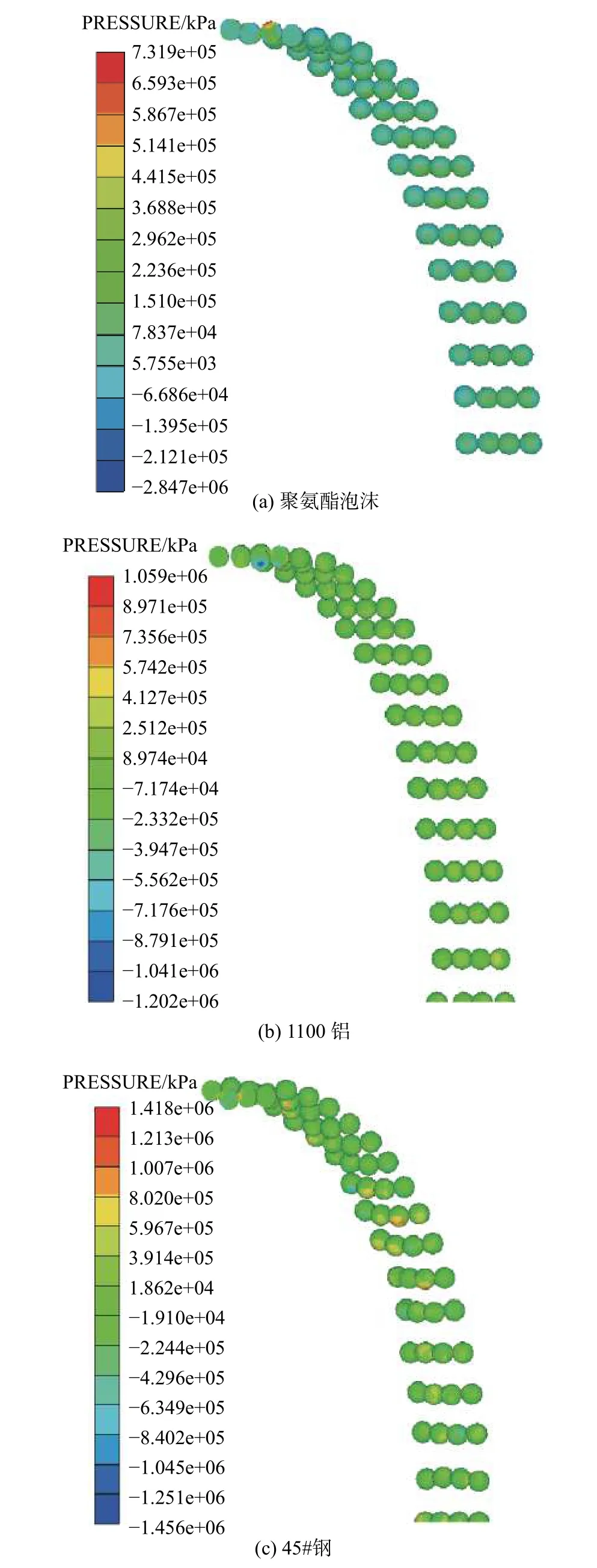
图5 直径2 mm球形破片不同内衬工况下破片压力云图

从压力峰值分布看，高压力区均位于与装药接触一面的破片底部。同质量装药不同内衬材料条件下，同尺寸破片受到的压力差别较大，峰值差距达94%。可知20 µs时刻三种内衬破裂程度各异：聚氨酯泡沫爆炸瞬间破裂，爆轰产物很早泄露，破片受到的压力最小；铝与钢材料相比破裂半径小，受到的压力值相对钢内衬低。图6给出了三种工况破片速度-时间曲线，由动量定理可知，破片受到的压力值与破片获得的动量正相关，压力值大的工况破片获得的初速也高。

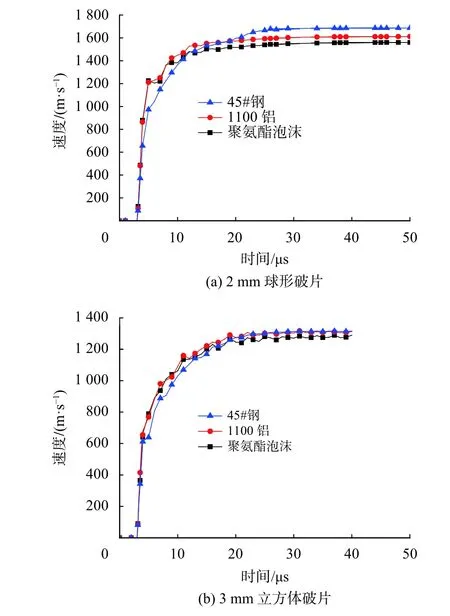
图6 两种典型破片不同内衬工况下破片速度曲线

对于2 mm球形，内衬45#钢对应的破片速度大于1100铝对应的破片速度，而对于3 mm立方体破片，两种内衬材料下速度接近，分析认为由于材料延展性好、膨胀破裂半径大，内衬45#钢时破片体应能获得更大动能，破片初速更高，但立方体破片与内衬贴合性相对较差，较球形破片气体泄漏更严重，导致多加载到破片体的能量更多被内衬材料或泄漏的气体获得，因此45#钢内衬时破片初速未见明显差别。

从图5中可知破片初速从高到低的顺序为：(内衬材料) 45#钢>1100铝>聚氨酯泡沫；而装填比大小顺序却是(内衬材料)45#钢<1100铝<聚氨酯泡沫。若采用经典的Gurney公式计算，破片速度基本取决于装填比，计算结果与图6完全相反，与实际情况不符。可见选取不同内衬材料进行预制破片初速研究具有实际应用价值。聚氨酯泡沫和45#钢内衬工况破片初速理论及数值模拟结果见图7。

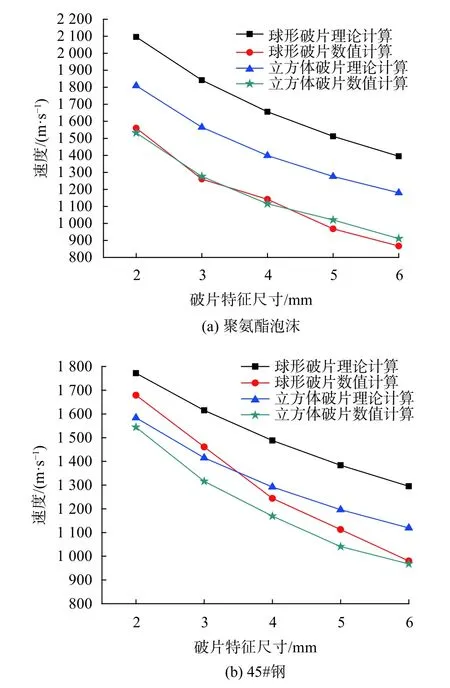
图7 不同内衬材料下破片初速理论及数值模拟结果

可见排布和驱动过程中存在气体泄漏等问题，导致现有的理论模型计算结果明显偏高。

2.4 模型建立

根据气体泄露系数的量纲分析结果，对数值模拟得到的破片初速结果进行处理，便得到数据拟合所需的数据，见表4和表5。

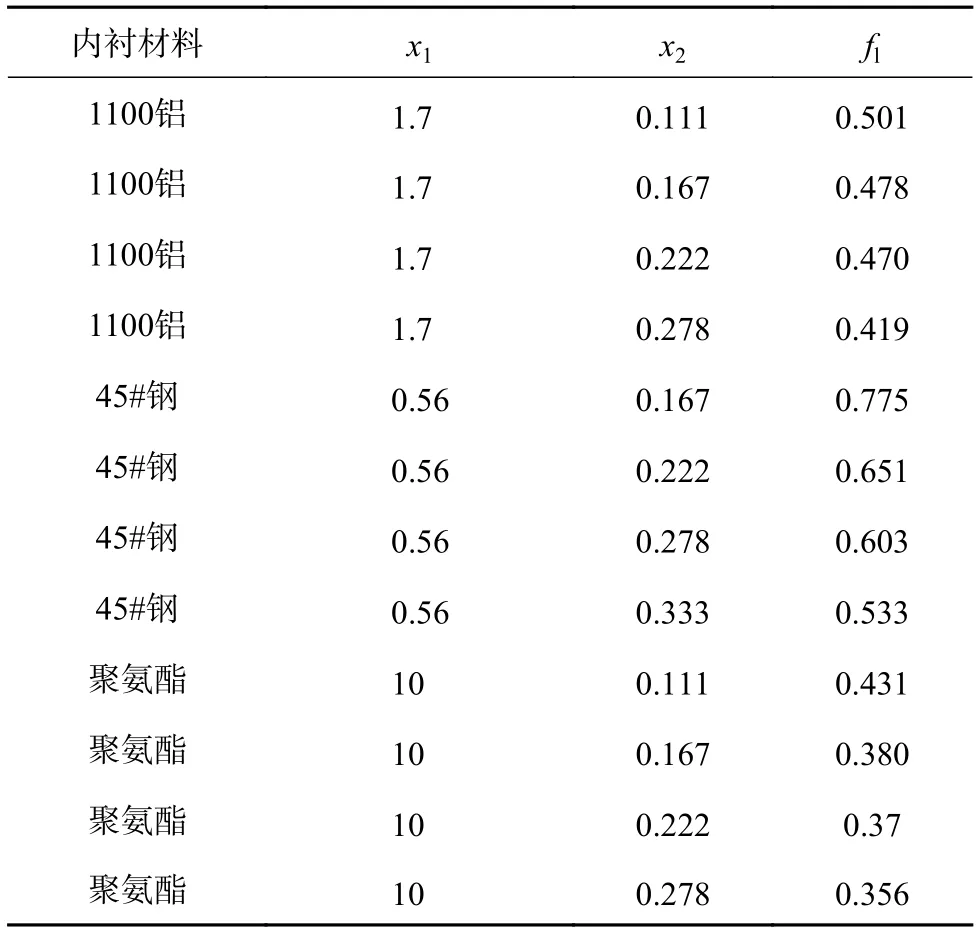
表4 球形破片气体泄漏系数拟合数据

表5 立方体破片气体泄漏系数拟合数据

对气体泄露系数fl进行多项式拟合，公式形式如下式所示，a1～a3、b1～b3、d为待定系数。

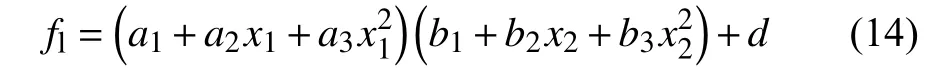
对两种不同形状的破片进行拟合计算，获得曲线见图8，拟合得到的参数见表6。

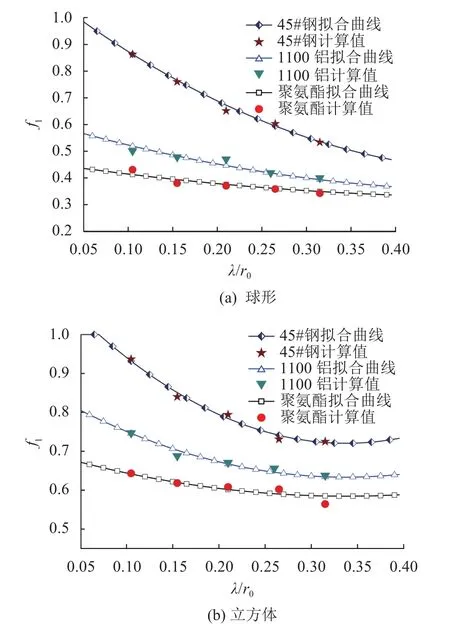
图8 不同形状破片fl系数拟合曲线

表6 不同形状破片初速公式参数拟合结果

考虑到数值模拟中内衬材料范围及破片与装药半径的相对尺寸，给出预制破片初速模型的定义域为 0.56≤x1≤10，0.05≤x2≤0.32。

3 试验研究

设计的预制破片装置主要由前后端盖、装药、破片和内衬等件组成，预制破片放置于单端加工有凹槽的聚乙烯圆筒中，结构示意和实物如图9所示。选取的装药为JH-2药柱，装药半径18 mm，长度50 mm，工况 1、3、5选取Ф5 mm 破片内衬分别选取45#钢、聚乙烯和1100铝三种材料；工况2、4、6选取Ф6 mm破片内衬分别选取45#钢、聚乙烯和1100铝三种材料，内衬尺寸与数值计算工况相同。

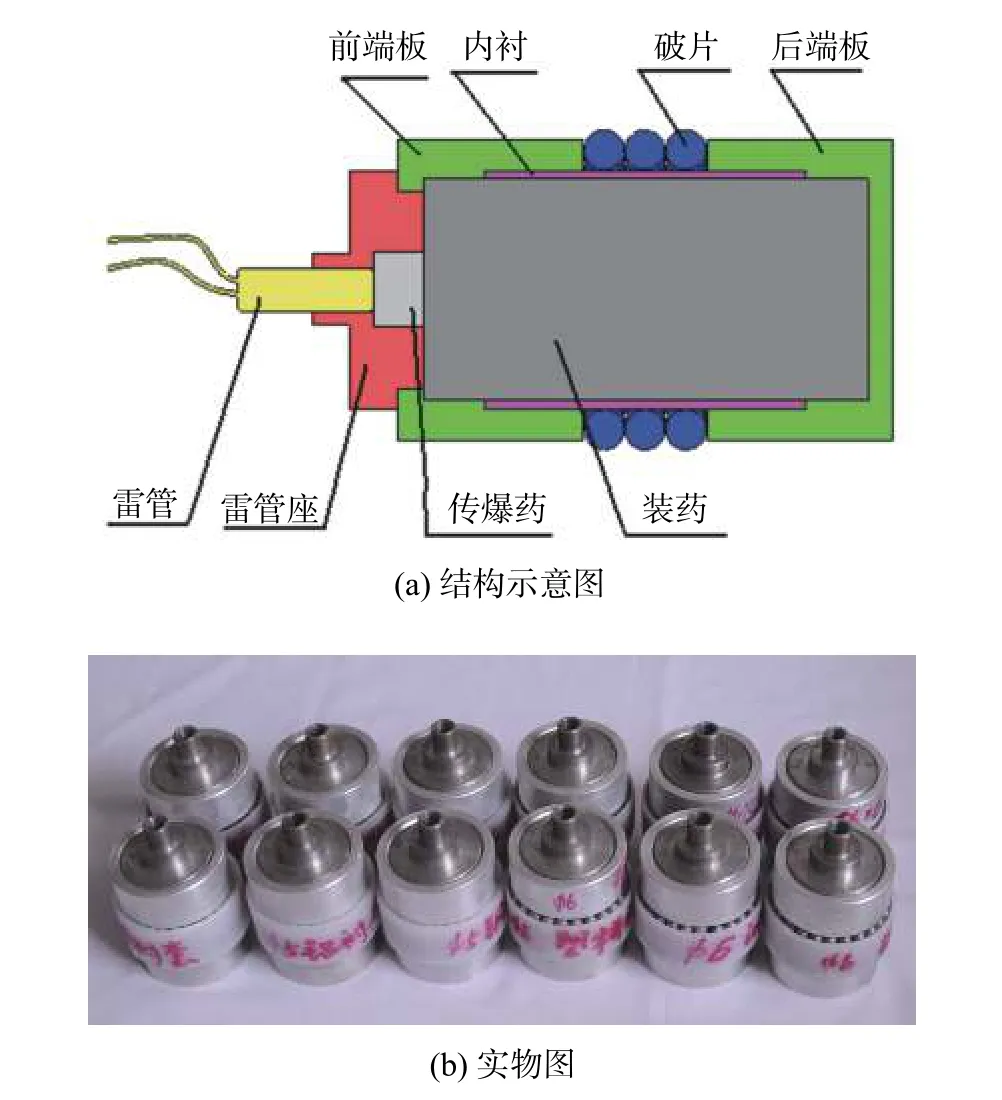
图9 试验装置

试验在爆炸洞中进行，预制破片装置轴线向上放置于中间支撑杆之上，装置中心距离地面0.5 m，与测速靶中心平齐。为了获得准确的破片初速结果，分别在距离装置2 m和4 m处布置了两组梳状测速靶。试验现场布置如图10所示。

图10 静爆试验现场布置

试验中取测得数据的最高值作为破片速度值。对于不同工况两公式计算与以上试验结果及文献试验结果的对比情况汇总如表7所示，其中立方体破片数据引用文献[11]的试验结果。

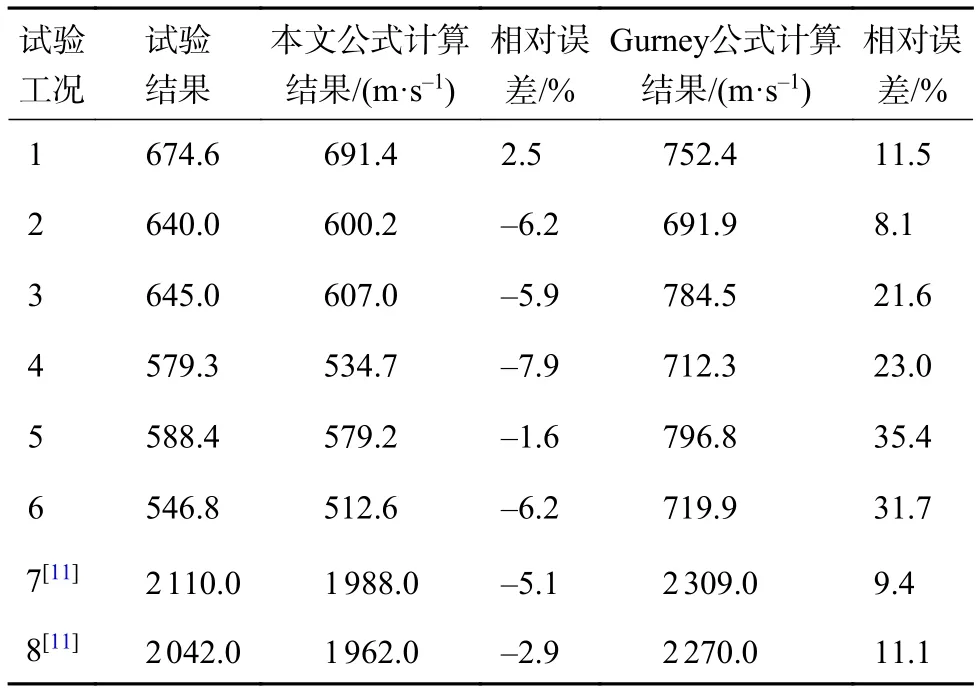
表7 试验结果与计算结果对比

从以上结果及分析可知，经典的预制破片初速公式计算钢内衬工况时误差相对小，其他内衬工况误差均超过20%；与经典的预制破片初速公式相比，本文提出的预制破片初速修正模型由于考虑了内衬材料、破片形状和尺寸的影响，与试验结果符合度更好，模型大大降低了经典公式的计算误差，精度平均提高了14%以上，可用于预制破片初速的工程计算。

4 结束语

1)爆轰产物泄漏对炸药驱动预制破片速度有一定影响，随着内衬材料特性、破片形状和尺寸等参数的调整，预制破片初速呈现相关性变化。

2) 通过在经典公式基础上增加爆轰产物泄漏系数，本文构建了一种预制破片初速的修正计算方法并通过了试验验证，结果显示相比原公式精度平均提高14%以上。

3)本文结论对于预制破片战斗部设计和毁伤威力准确评估具有实际的指导意义。