考虑非机动车影响的直线式单泊位公交停靠站设置优化*

李英帅 马泽超 王雯婧 王卫杰

（1.南京工业大学交通运输工程学院 南京211816；2.重庆交通大学交通运输学院 重庆400074）

0 引言

近年来，随着共享单车与电动自行车的普及，非机动车出行在市域出行中的比例显著增长，增加了交通秩序管理的压力。尤其是在公交停靠站周边区域，各种交通方式相互干扰和冲突，严重降了低公交停靠站的使用效率及安全性。通过对各类公交停靠站进行研究得出：沿人行道设置的直线式公交停靠站周边区域受非机动车的影响最严重。公交车停靠时，会与非机动车发生交汇，产生交通冲突，造成交通流延误，并且使公交停靠站的安全性降低。为了提高公交停靠站的交通效率和安全性，有必要对公交停靠站的设置进行优化。

对于非机动车在公交停靠站周边区域与公交车相互影响方面，R.J.Jilla[1]研究发现当公交车经过非机动车时，公交车速度会降低，位置也会发生横向偏移。P.Cazorla[2]分析公共汽车与自行车共享车道（SBBLs）设计指南在欧洲、北美和澳大利亚的应用，研究表明：自行车基础设施的类型、SBBL内的线形和车道宽度是确保这2种模式安全和高效的参数。S.Reid等[3]在英国的3个城市调查了在公交车道上的自行车与公交车相互影响的规律，调查发现：公交车与自行车在较宽的公交车车道（3.8 m相比于3.1 m）处的延误显著减少。Zhao等[4]提出了1种基于元胞自动机（CA）模型的方法来模拟路边停车点周边的混合流，并讨论了公交车停车时间等参数对交通的影响。杜少娜等[5]研究了北京市2个不同的典型公交站，分析了公交站周边区域自行车对公交车的干扰行为，并建立了自行车对公交车的干扰行为模型,但欠缺对公交停靠站几何特征的分析。王欢[6]对公交停靠站周边区域进行功能划分，建立了机非混行交通流模型，仿真并分析了公交站周边区域机非混行车流的相互影响。韩志玲等[7]分析非机动车在公交停靠站处对公交车进站、停靠、出站等延误的机理，并构建模型，对照分析非机动车在直线式公交停靠站和准港湾式公交停靠站处的干扰影响差异。其研究显示：非机动车流将造成直线式公交停靠站的服务时间增加约26.4%，停靠时间增加约24.7%，表明直线式公交停靠站周边区域机非冲突问题比较严峻。

交通冲突是非机动车与公交车相互影响的主要方式，一些学者对此开展了研究。Zhao等[8]对中国4个不同类型的公交停靠站进行了实地调查，并建立了公交车与自行车冲突预测模型，用于评估公交车与自行车共享设施的可行性。研究发现：即使很难从左侧通过，也很少有骑车者愿意在停车的公交车后面等待。近50%的骑车者选择从右侧穿过路缘和公交车之间的空隙，超过停在路边的公交车。此外，该模型中公交的停靠时间为1个定值。然而，Lu等[9]研究发现公交的停站时间受车站附近的几个因素影响。Luo等[10]提出了1种元胞自动机模型，用于模拟公交站点附近由机动车和自行车组成的混合交通流。仿真结果表明：在临界点处，机动车和自行车的流量均表现出从自由流动到饱和流动的相变。都舒[11]研究了北京10个公交停靠站，选取几何特性和交通流特性中4个因素对非机动车在公交站周边区域发生的3种交通冲突进行影响分析，并建立冲突指标，以此对非机动车在公交站周边区域行驶进行安全评价。但其调查的冲突相关因素的拟合精度R2较多小于0.4，精度较低，选取的冲突因素相关性较差。王柯婷[12]通过调查，分析在公交停靠站周边区域的混合交通流特性，解析各种交通方式间的冲突机理和冲突延误时间。罗铮等[13]研究了公交停靠站处产生交通冲突的原因，指出要解决公交停靠站周边区域的冲突，需要依靠整体协调规划结合局部管理的方法。

交通冲突会引发事故风险，因此，一些学者对非机动车风险行为进行分析。范爱华[14]利用生存分析方法，研究了非机动车在公交停靠站周边区域不同风险行为规律。李萌[15]运用生存分析法构建了非机动车越线行为Cox比例风险模型，分析出5个对非机动车越线行为的显著影响因素，运用SPSS统计软件分析了非机动车在公交停靠站附近的分布特性，由几何条件引发的相对风险率大于2，以及自行车数量比例对应的风险率为0.92，可知对非机动车越线行为影响较大的是公交停靠站设计与机动车流量等因子。邵海鹏等[16]针对2轮车在公交停靠站附近的穿插行为，观察了896组实验数据，得出公交车辆停靠站时2轮车穿插行为的8个影响因素，在此基础上建立了贝叶斯网络模型，分析各变量对2轮车穿插行为的概率分布。

部分学者对公交停靠站进行优化设计，以期改变公交停靠站周边交通参与者的交通行为，提升交通秩序。如田春春[17]建立了路段流量较大时的公交停靠站类型的优化选择模型。孙明东[18]选用延误模型，得出公交停靠站的选型模型以及公交停靠站长度与宽度优化方法。模型从延误效率的角度出发，为公交停靠站改建的条件提供了依据。

综上可知：针对公交停靠站周边区域交通秩序混乱、事故风险高的现象，从非机动车与公交车的相互影响、交通冲突、风险行为，以及公交停靠站设计优化等方面进行研究，指出了研究公交停靠站周边机非冲突可选用的调查因子及其可行性，公交停靠站周边区域交通延误和通行水平，以及站点优化改建措施等。但其研究结果存在所选用的部分调查因子对机非冲突率的影响并不显著、整体拟合模型精度较低等问题。笔者从非机动车与公交车的冲突着手，以沿人行道设置的直线式单泊位公交停靠站为研究对象，探究公交停靠站几何特性、交通流特性与冲突率的关系，以降低冲突率作为公交停靠站设置优化的目标，对直线式单泊位公交停靠站的设置进行优化。

1 数据采集与分析

1.1 调查方案设计与实施

调查的主要目的是研究公交停靠站几何特性及其周边区域交通流特性对冲突率的影响。通过调查，将公交停靠站周边区域的冲突根据行车轨迹和冲突空间分为3类：①公交车由机动车道变换到非机动车道时，与非机动车发生的侧向及追尾冲突；②公交车停靠时，占用机动车道的非机动车和机动车发生的侧向冲突；③公交车加速离站时，公交车与从外侧绕过的非机动车发生侧向及追尾冲突。

调查时间选择在2020年5月—6月的每周四、周五的早、晚高峰（08：00—10：00、17：00—19：00），每5 min作为1个调查周期。调查地点为重庆市6个沿人行道设置的直线式单泊位公交停靠站，并要求公交停靠站在路段上且不是起终点站。调查采用人工计数法，内容为公交车与非机动车的车道宽度、交通量、速度、冲突类型与数量、公交车停靠时间、公交停靠站几何特征参数等。

1.2 调查数据处理与分析

将非机动车道宽度、公交停靠站长度、非机动车速度、当量交通量与3类冲突率进行回归分析得出回归分析方程，以及相关关系图。

1.2.1 冲突率与非机动车道宽度的关系

冲突率与非机动车道宽度具有一定的相关关系，见图1。

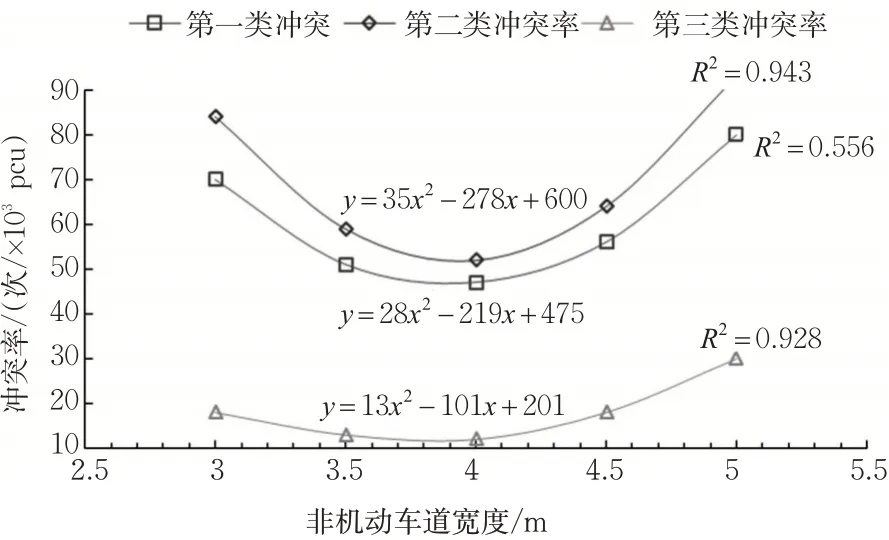
图1 冲突率与非机动车道宽度的关系Fig.1 Relationship between the conflict rate and non-motorized lane width

经过二阶多项式回归分析后，3类冲突率随非机动车道宽度的增加均呈现先降低再升高的趋势。对于第一类冲突率，非机动车道宽度在4.0 m时达到最低值，对于第二类、第三类冲突率，非机动车道宽度均在3.9 m时达到最低值。

1.2.2 冲突率与公交停靠站长度的关系

冲突率与公交停靠站长度的相关关系见图2。

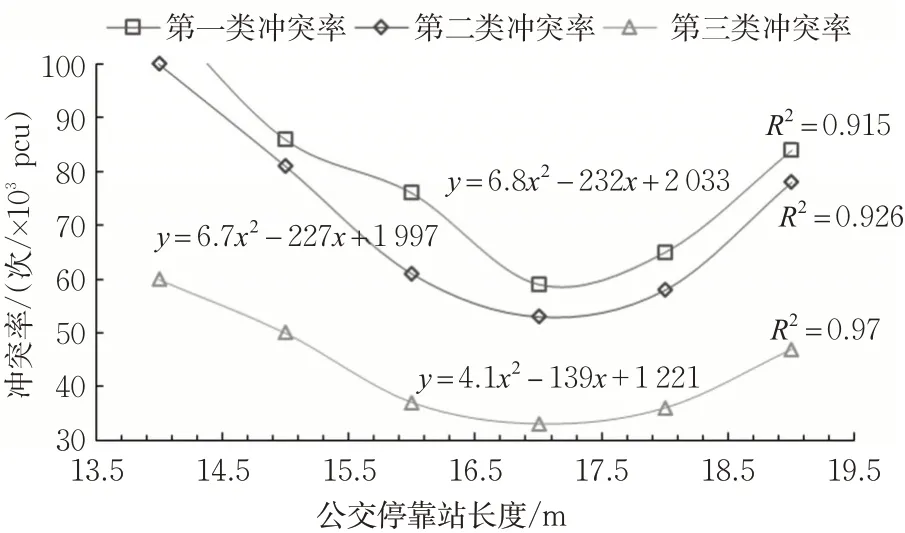
图2 冲突率与公交停靠站长度的关系Fig.2 Relationshipbetweentheconflictrateandlengthofbusstop

经过二阶多项式回归分析后，3类冲突率随公交停靠站长度的增加均呈现先降低再升高的趋势，并且3类冲突率均在公交停靠站长度约17.0 m时达到最低值。

1.2.3 冲突率与非机动车速度的关系

冲突率与非机动车速度的相关关系见图3。

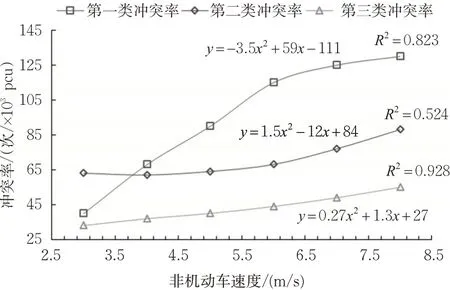
图3 冲突率与非机动车速度的关系Fig.3 Relationship between the conflict rate and non-motorized vehicle speed

经过二阶多项式回归分析后，第一类与第三类冲突率均随非机动车速度的增加而增加。第二类冲突率随非机动车速度的增加先呈现微弱的降低（车速为4.0 m/s时达到最低值）后增加的趋势。当非机动车速度在6.0 m/s以下时，第一类冲突率增长速度明显快于另外2类；而当速度高于6.0 m/s时，增长速度趋于平缓。第三类冲突率增长速度比较平稳。

1.2.4 冲突率与当量交通量的关系

冲突率与当量交通量的相关关系见图4。

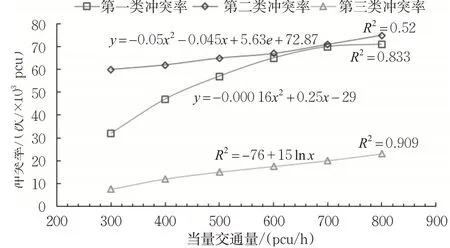
图4 冲突率与当量交通量的关系Fig.4 Relationship between the conflict rate and equivalent traffic volume

经过二阶多项式回归分析后，3类冲突率均随着当量交通量的增加而增加。其中，第一类冲突率在当量交通量达到700 pcu/h之前，增长速度较快，之后，冲突率趋于平稳。第二类冲突率与第三类冲突率随当量交通量的增加而平稳增加。

2 交通冲突预测模型

2.1 冲突预测模型建立

以非机动车道宽度、公交停靠站长度、当量交通量、非机动车速度为自变量，以第一类冲突率、第二类冲突率、第三类冲突率为目标函数，建立冲突预测模型，见式（1）。

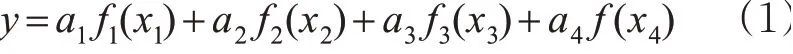
式中：x1为相邻非机动车道宽度，m；x2为相邻机动车道的当量交通量，pcu/h；x3为非机动车平均速度，m/s；x4为公交停靠站长度，m；f1，f2，f3，f4为为相应影响因素的冲突率函数；a1，a2，a3，a4为对应相关系数。

选取调研数据中多组数据作为预测数据，得到3类冲突预测过程及结果如下。

第一类冲突率预测模型根据式（1），用A表示相关系数，则

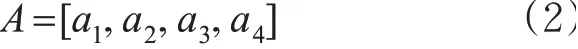
经过一元回归分析，得到各个因素的影响函数，由此可知第一类冲突的影响函数为

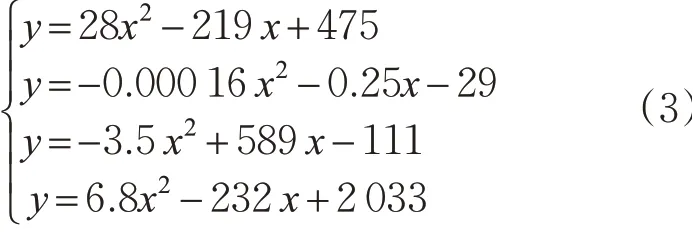
使用SPSS软件经“分析-相关-双变量”步骤，得到4个自变量和第一类冲突率的相关系数。经过多元回归分析计算可得相关系数A。

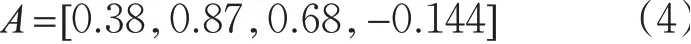
即公交车进站时第一类冲突率的预测模型见式（5）。

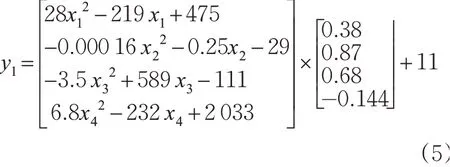
经上述步骤重复操作得到第二类冲突率和第三类冲突率的预测模型见式（6）~（7）。

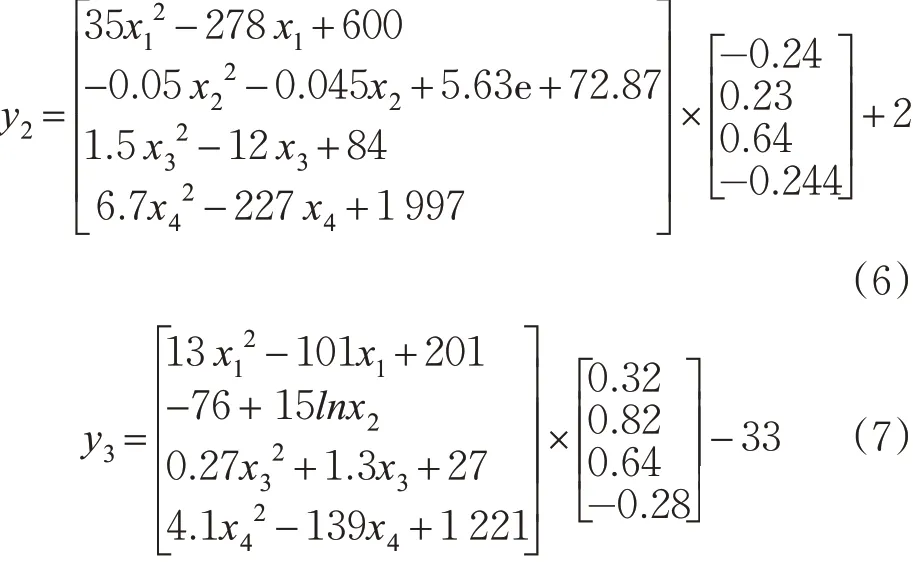
2.2 验证预测模型

取同期调查时未被选用模型建立的数据进行验证，验证结果见表1。

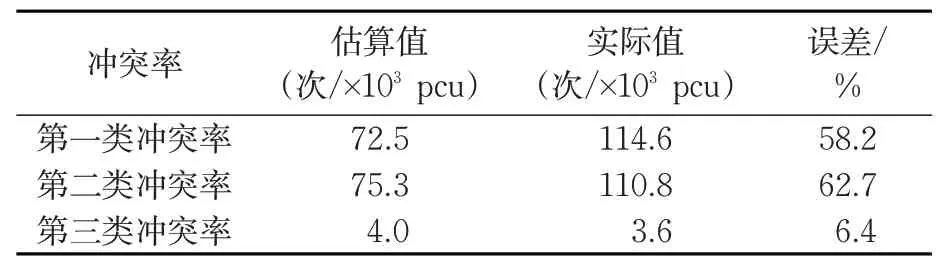
表1 公交停靠站交通冲突率估算值与实际值对比结果Tab.1 Comparison results of traffic conflicts between estimated and actual values at bus stops

在该站的冲突率记录中，存在人为主观因素的干扰和现实情况的差异，造成了该站第三类冲突率的误差较大，不过，所有误差均小于10.0%，满足统计学中一般情况下的精度要求。从模型结果可以看出，交通冲突预测模型具有一定的精度，可以用于预测交通冲突的实际值。

2.3 预测模型可视化

利用基于Python的图表绘图系统Matplotlib创建本文所得数学模型的互动可视化模型。将调查所得的公交停靠站站长和非机动车道宽度范围作为冲突率的x和y区间，将非机动车速度和相邻车道当量交通量作为输入变量，以灰度作为冲突率变化展现（灰度越浅冲突率越高），即可得到含有该4类变量的冲突率预测模型。见图5。

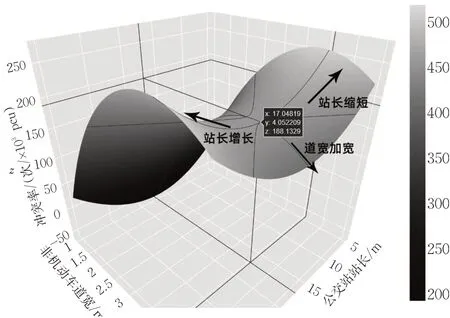
图5 可视化预测模型Fig.5 The visual prediction model

利用可视化插件进行计算，从1.2中的冲突率与4个变量因素的关系图中，选取最低冲突率时的当量交通量与非机动车速度，即选300 pcu/h和3.75 m/s作为第三和第四类影响因子的值。选取1.2中冲突率和公交停靠站站长与非机动车道宽度相关关系图中的最低值，即公交停靠站站长17 m与非机动车道宽4 m。根据图中数据可得冲突率为188，符合临界安全等级。在当实际条件无法全部满足时，由模型数据可知，其具有较为宽泛的调整空间以供站点进行多方向的优化改进，即可沿自变量的方向进行移动，根据冲突率的变量，选取可接受的次优方案。

2.4 预测模型延误分析

公交车在机非混行直行式公交停靠站停靠时，常占用非机动车道停靠，因而对相邻机动车道交通流产生的影响较小。

当4个影响因素分别取冲突率最低时所对应的数值时，公交车停靠站周边区域的冲突率最低，安全等级最高，此时，公交车与非机动车对周边的机动车延误影响均最小。

3 公交停靠站安全性优化

3.1 安全等级划分

参考文献[11]，对总共统计过的十余个公交停靠站点的交通冲突率使用数理统计分析的方法，分析冲突率的累计百分频率，确定不同累计百分率对应的数值，作为灰类的白化值。引入公交停靠站的安全状况可分为特别安全（A）、安全（B）、临界安全（C）、不安全（D）、特别危险（E）这5个级别，分别为15%、40%、60%、85%。根据总冲突率累计频率曲线图划分安全等级，见图6和表2。

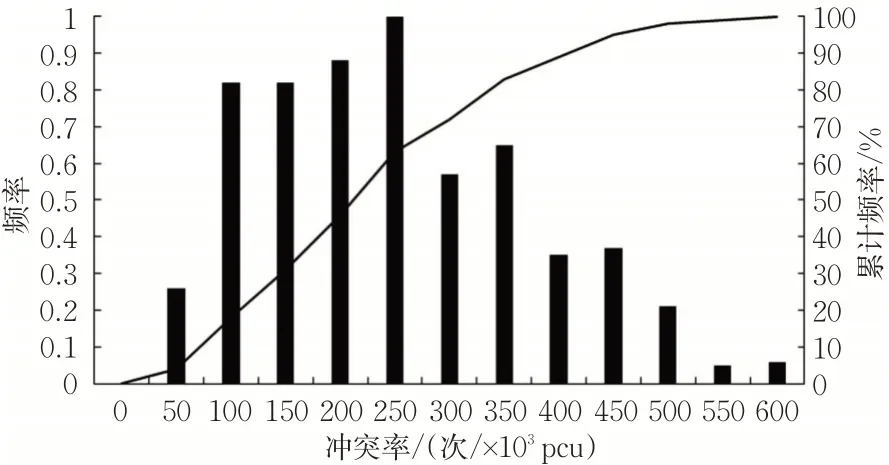
图6 冲突率频率分布及累计频率曲线Fig.6 Frequency distribution of conflict rates and cumulative frequency curves

表2 安全等级划分Tab.2 Safety classification

3.2 冲突率评价

得到冲突率的多元回归方程和安全等级划分后，再次选取2个非上文提及的符合设置形式的直线式单泊位公交停靠站进行调查。选取虎溪站及大学城U城站这2个沿人行道设置的直线式单泊位公交停靠站进行分析，其几何特征和交通流特性见表3。

表3 实例公交停靠站几何特性及交通流特性Tab.3 Geometric characteristics and traffic flow characteristics of sampled bus stops

虎溪站和大学城U城站冲突预测结果见表4。选取的2个公交站的总冲突率为274.3，160.1。根据安全等级的划分，虎溪站处于不安全状态，大学城U城站处于安全状态。

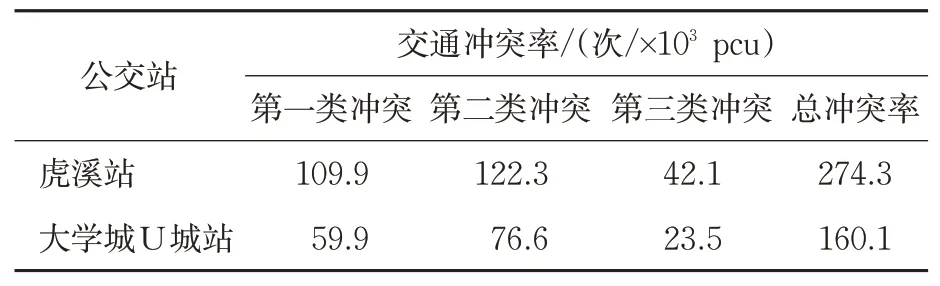
表4 实例公交站交通冲突预测对比Tab.4 Comparison of prediction of the traffic conflicts of sampled bus stops

3.3 应用方案改进

从公交停靠站的交通冲突率计算结果可以得出：虎溪站的第一类冲突与第二类冲突比例较高。从实际出发，结合公交停靠站几何特征以及交通流特性进行分析，虎溪站处于路段上，且机动车道为2幅路。由于非机动车道较窄，非机动车容易与公交车发生侧向或者追尾冲突，甚至非机动车会占用人行道行驶。在该公交停靠站周边区域，交通冲突较多且非机动车速度受限制也较少，部分非机动车速度较快，增加了非机动车的第一类和第二类冲突率。

综合各方面情况的考虑，提出虎溪站的改善建议：①适当拓宽非机动车道宽度，将3.3 m拓宽为3.5 m；②适当增加公交停靠站的长度，将14 m增加到17 m；③对非机动车速度进行标志控制，不得高于3 m/s。虎溪公交站改善建议的几何及交通流特征见表5。

表5 虎溪站公交停靠站改善建议值Tab.5 Suggested design values for improving Huxi bus stop

对采取措施后的公交停靠站进行冲突率计算，计算结果见表6。

表6 虎溪站改善后交通冲突率预测值Tab.6 Predicted values of traffic conflict rates after the improvement of Huxi stop

通过模型检测，改善后的虎溪公交停靠站冲突率有明显的下降，安全状况由不安全变为临界安全，则说明以上改善建议能够提高公交停靠站的安全性。

3.4 站点优化措施

在一般条件下，公交停靠站站长的可变动空间是充足的，对其优化改建通常不会受到空间限制的影响，因此，可以对站长长度进行优化，以此降低冲突率。而针对非机动车道横向宽度的改进，可以首先通过压缩路边绿化带的方式实现，必要时可取消该站点周边的绿化带设置。

若该站点的周边道路空间极为有限，以至于不满足公交停靠站做任何形式的横纵向改建，则说明当前条件下该路段的服务水平将不再满足未来公交运行安全性和效率的要求，需对该站点的位置布局、原公交路线运行效率、延误水平等因素进行评价，可选择对该地区进行较大规模的路段重建措施，或选择将站点迁移至不严重影响原公交路线效率的、且存在改建空间的路段。

若该站点的周边道路空间极为充足，允许该站点进行大规模形态改建工程，可在3类变量均优化到最低冲突率但整体安全性仍未达标时，对该站点进行较大规模的形态改建。该站点可选择改建为港湾式公交停靠站，或在公交停靠站后方专门设置1条绕行公交站的非机动车辅道，辅道宽度控制在2 m左右，以保障自行车（单条非机动车道宽度：1 m）、电动车（1.25 m）、3轮车（2 m）的行车要求，用以分流通过公交站点前方的非机动车流，降低整体冲突数，提高站点的安全性。

相对于站点几何条件，非机动车行车速度存在人为变量的因素，对其的限制效果较难把握，故应当在站点几何条件都达到最低限制时，再对非机动车速度进行严格的限制。可采用非机动车限速的标志标识引导、实时速度检测与拍照公示并行等措施。

4 结束语

1）随着非机动车道宽度和公交停靠站长度的增加，3类冲突率呈现出先减小后增大的趋势。得出沿人行道设置的直线式单泊位公交停靠站设置长度的建议值为16~18 m，非机动车道设置宽度建议值为3.5~4 m。

2）随着当量交通量以及非机动车速度的增加，3类冲突率呈现出持续增加的趋势。得出在沿人行道设置的直线式单泊位公交停靠站，非机动车速度应该低于6 m/s，并保障非机动车道宽度维持在4 m左右，为非机动车留出足够的行车空间和冲突规避区。必要时可设置减速设施，提醒非机动车减速。

对直线式单泊位公交站进行冲突优化设计时，基于站点几何条件和道路交通运行状况出发的限制性改进，可在保持公交停靠站延误效率最优的选型模型的基础上，改建过程不会长时间影响公交停靠站运营，同时可节约改建成本。