公交站台区域电动自行车与行人通行冲突演化博弈模型*
周 旦 姚威振 顾国斌 胡清玮
(桂林电子科技大学建筑与交通工程学院 广西 桂林541004)
0 引言
目前,我国公交站台通常设置于非机动车道和机动车道之间的隔离带位置,公交乘客进出站台需横穿非机动车道,易与抵达车辆抢占通行权,产生相互干扰、冲突甚至碰撞。非机动车道中电动自行车占比大、行驶速度快,导致过街乘客处于较为危险的交通环境中。当前针对公交站台区域的交通问题研究多集中于站台形式、停靠方式、设置位置等因素对相邻机动车道的通行能力的研究[1]。孙锋等[2]、刘路等[3]利用排队论分别建立计算模型探究不同站台形式和停靠方式对机动车路段通行能力的影响;Zhang等[4]针对公交站台位置和出入口组合对快速路通行能力的影响进行了研究。针对不同公交站台的设置形式、进出站乘客对非机动车运行的影响问题。闫星臣[5]在基于事故预测的自行车乘客冲突模型中分析了对公交站台区域冲突数影响的关键参数,探究设置公交站台的非机动车道通行能力的影响因素。平萍等[6]建立基于人非冲突概率的非机动车道在进出站乘客影响下的基本通行能力模型,从量化层面,探究了乘客与非机动车之间冲突对非机动车道通行能力的影响。针对行人与非机动车之间的冲突问题,Beitel等[7]以加拿大麦吉尔大学校园为例,使用计算机视频识别软件提取使用者轨迹,分析了行人与自行车共存时的冲突风险。文夏梅等[8]对城市混合共享街道使用者的微观行为特征研究发现,电动车较易与行人发生碰撞,并在低流量时段对行人的过街造成更大威胁。
倪颖等[9]研究指出,电动自行车和行人在通行时具有集群交通特性,同时出行者的交通行为选择又会受到经验、交通信息和个人习惯等因素的影响,所以电动自行车和行人是有限理性的交通群体。公交站台区域过街乘客和电动自行车之间的群体冲突并非1次性活动,存在信息反馈的决策过程,交通参与者根据实时交通信息进行适应性学习。交通参与者之间存在着相互影响和策略互动,可认为双方存在博弈关系。
演化博弈较经典博弈论,突破了完全理性假设的局限,从人的有限理性出发来分析预测群体的行为。目前演化博弈应用的领域越来越广泛[10-11]。蔡鉴明等[12]在对城市居民中长距离出行方式的研究中引入演化博弈理论,分析相关参数对演化过程的影响;窦水海等[13]构建信控交叉口处交通参与者穿越行为的长期演化模型,探究了交通参与者的收益、损失变化对交通行为演化结果的影响;Zhang等[14]运用演化博弈的思想研究了人行横道多群体行为的演化规律,分析了行人过街过程中的交通主体行为,为解决路段人行横道处的交通利益冲突提供了新思路。因此可以用演化博弈理论来研究有限理性条件群体学习过程[15]。
目前关于人-非群体冲突的安全性研究相对缺乏,在城市交通共享区域,交通参与者的通行行为对交通安全有着重要影响[16],行人的路边等待时间与行人的过街风险存在相关性[17]。所以本研究从冲突产生的时间延误出发,建立演化博弈模型,对不同交通环境中交通参与者发生冲突时通行行为演化过程进行研究分析。
1 延误模型构建
以公交站台区域进出站台的行人和通行的电动自行车为研究对象,基于电动自行车群车头时距概率分布特点和车流波理论,建立行人过街时间延误模型和电动自行车通行时间延误模型,量化冲突过程中行人与电动自行车的延误时间,直观反映不同交通状态下的各交通参与者选择的通行行为对其通行效率的影响。
1.1 行人过街时间延误模型
行人延误为行人在公交站台区域的非机动车道边缘处等待电动自行车群之间出现可穿越间隙的等待时间。进出站台的行人在准备穿越非机动车道时,需要判断电动自行车之间是否存在安全间隙以满足自身安全通行的需求。如果存在,行人直接穿越;否则,需要等待出现安全间隙才可以完成穿越,见图1。在这个过程中,行人判断是否存在安全间隙的时间为tr,如果电动自行车间隙小于行人的安全通行间隙ta,此时行人选择等待而消耗时间为T,即为行人选择等待策略的延误时间。由于电动自行车存在集群效应,前后车辆之间的车头时距较小时,后面跟随的车辆可以穿插到前方车辆之间的空隙中,此时车辆之间的相互影响作用强烈,则定义这些车辆处于1个群体中。在这样1个电动自行车群体通过公交站台区域时,行人无法穿越过街,只能选择等待。为简化行人对电动自行车间隙的判断过程,认为行人只对电动自行车群之间的群车头时距进行判断。相邻的2个车群之间的群车头时距大于行人过街可接受临界时间间隙ta时,行人选择过街。电动自行车之间处于稳定交通流状态时,若车头时距大于0.4 s时[6],车辆之间的运转比较灵活,彼此作用减小。选择0.4 s作为电动自行车群车头时距的划分阈值,得到电动自行车群车头时距概率密度分布函数为f(t)。则行人在面对1个电动自行车群间隔时,可以通行的概率为;行人需要等待k个车群间隔,在第k+1个间隔通过的概率为:
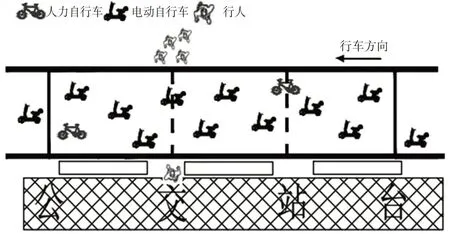
图1 行人等待过街示意图Fig.1 Pedestrians waiting to cross the street
Pk+1=(1-P)k P;所 以 人 均 等 待 间 隔 数行人作为有限理性的交通群体,面对1个电动自行车群间隔时,如果选择等待,那么这个间隔必定小于行人可接受过街临间隔ta,此时行人需要等待的平均时间为:


式中:P为行人可通行概率;k为行人等待间隔数,个;Xˉ为行人平均等待间隔数,个;tˉ为行人每个间隔平均等待时间,s;ta为行人可接受时间间隔,s;T为行人选择等待的总时间延误,s。
1.2 电动自行车通行时间延误模型
行人在穿越非机动车道时,上游到达的电动自行车感知到行人的干扰进行减速以避免与行人产生冲突。见图2,在区域I中,电动自行车驾驶员对交通环境进行判断以后选择减速,并由最初的速度v1变化到v2;在区域Ⅱ中,电动自行车以v2速度大小行驶,直至行人完全横穿非机动车道;在区域Ⅲ中,因为行人的干扰导致电动自行车流出现断层,前方路段没有交通参与者,所以电动自行车选择自由流速度v3运动。
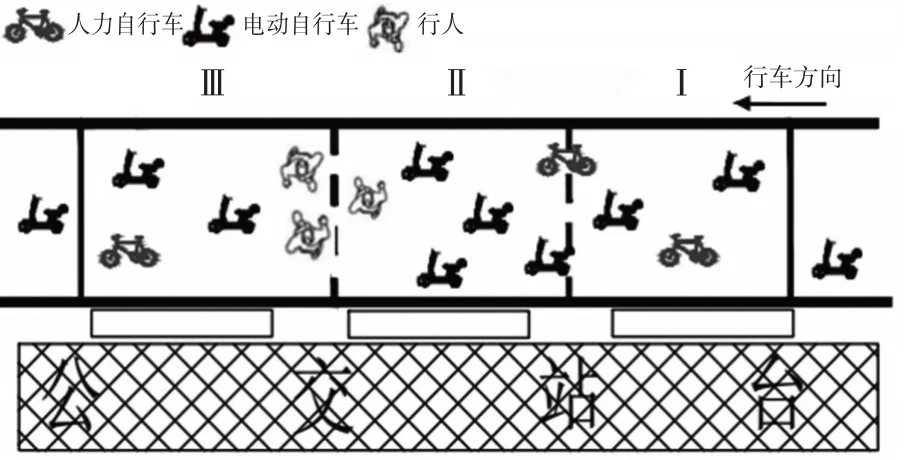
图2 电动自行车减速示意图Fig.2 Electric bicycle deceleration
根据运动学知识,电动自行车在区域I减速过程中产生的延误为dd=(v1-v2)2/(2adv1),在区域Ⅲ加速过程中的延误为db=(v3-v2)2/(2abv3)。
在区域Ⅱ中,电动自行车减速导致车辆集结,根据车流波理论,电动自行车集结波速为:wm=;单位时间内集结的车辆数为:nm=(v2-wm)k2w。其中,w为非机动车道有效宽度。所以在行人穿越的过程中到达的电动自行车数量为:N0=nmta=(v2-wm)k2wta;在行人完成穿越过程之后,电动自行车加速驶离出现消散波,消散波速为:;单位时间内消散的车辆数为:nv=(wv-wm)k2w;则消散时长为:tv=N0nv;所以电动自行车受影响的总时间为:tj=tv+ta;受影响的电动自行车总数为:N=nmtj=(v2-wm)k2w·(tv+ta)。
分析可知:第1辆电动自行车在整个过程中的延误时间为:df=ta(1-v2v1),最后1辆车的延误时间为0,整体延误时间是关于到达时间的一次函数,函数的定义域为(0,tj),所以延误时间关于时间的函数为:d=-tdf tj+df;在任意时刻到达的电动自行车数量为此时刻车头时距倒数与时间的乘积,所以在(0,0+Δt)时间段内到达的车辆数为:n=QΔt,其中,Q为车头时距t=h时的概率,在△t内的期望值就表示这一段时间内的到达车辆数。积分得在整个时间段内受影响的车辆总数为N,所以车流波集结和消散过程的延误为
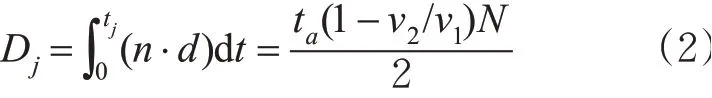
综上,电动自行车选择“减速”的时间延误为

式中:v1,v2,v3分别为电动自行车冲突前,冲突时,冲突后速度,m/s;q1,q2,q3分别为电动自行车流冲突前,冲突时,冲突后流量,veh/s;k1,k2,k3分别为电动自行车冲突前,冲突时,冲突后交通流密度,veh/m;ab,ad分别为电动自行车加速度和减速度,m/s2;db,dd分别为加速和减速时的时间延误,s;wm,wv分别为电动自行车流集结波速和消散波速,m/s;nm,nv分别为单位时间内集结和消散车辆数,veh;tv为电动自行车消散时长,s;tj电动自行车受影响总时长,s;w为非机动车道有效宽度,m;N0为行人穿越过程中集结车辆数,veh;N为受影响电动自行车总数,veh;df为第1辆电动车产生的延误,s;Dj为车流波集结和消散过程中产生的时间延误,s;D为电动自行车选择“减速”的总时间延误,s。
2 基于时间延误的演化博弈模型
演化博弈论是博弈理论和动态演化过程的结合,用于分析不完全信息演化的稳定性。通过复制动态方程求解得到演化稳定策略,具有较强的预测能力[18],可以用来分析公交站台区域的过街行人和电动自行车交通行为选择策略的变化趋势和演化的稳定性。演化模型做出3项假设。
假设1。在博弈过程中,行人和电动车自行视为独立的个体。
假设2。在公交站台区域,过街行人和电动自行车视为2个有限理性的交通参与群体。
假设3。在博弈过程中,电动自行车选择“穿越”的概率为p,选择“减速”的概率为1-p;行人选择“通行”的概率为q,选择“等待”的概率为1-q。
2.1 演化博弈模型收益矩阵
基于上述假设以及行人和电动自行车选择不同交通行为的时间延误,建立演化博弈模型。当行人和电动自行车选择“通行”和“穿越”时,二者可能发生冲突乃至事故,此时行人虽然付出了判断时间,但是未完成穿越的过程,所以认为此时行人的收益为-tr;电动自行车进行减速损失为判断时间和通行延误-tr-D;行人选择“通行”,电动自行车选择“等待”,行人收益为电动自行车减速产生的延误D,电动自行车收益为0;行人选择“等待”,电动自行车选择“穿越”,电动自行车收益为行人等待产生的延误时间T,行人的收益为0;行人和电动自行车分别选择“等待”和“减速”时,二者都不会产生收益,此时的收益都为0。过街行人和电动自行车收益矩阵见表1。

表1 过街行人和电动自行车收益矩阵Tab.1 Income matrix for pedestrians and electric bicycles
2.2 基于延误时间的演化博弈模型
电动自行车行为演化分析,电动自行车选择“穿越”时收益为:Ut=q( -tr-D)+(1 -q)T,选择“减速”时收益Uw=0,则电动自行车期望收益为Uˉ=p
根据演化博弈论的理论可知,电动自行车选择“穿越”的行为策略复制动态方程为
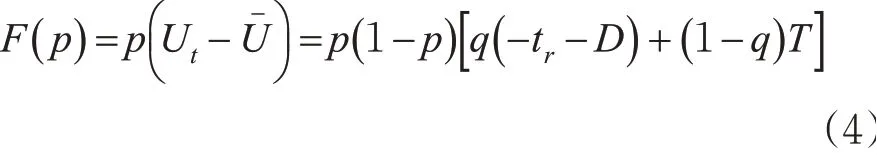
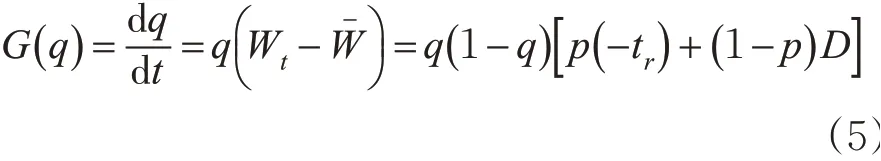
根据该演化博弈模型,对该系统雅克比矩阵的局部稳定性分析得出演化博弈均衡点的稳定性,由电动自行车和行人交通策略选择复制动态方程可得雅克比矩阵为
分析可得该矩阵对应的行列式det(J)和迹tr(J)为
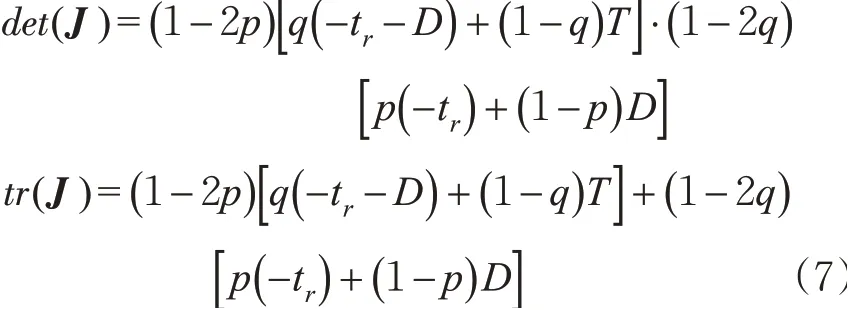
演化博弈过程稳定性分析见表2。

表2 均衡点稳定性分析Tab.2 Stability analysis of equilibrium points
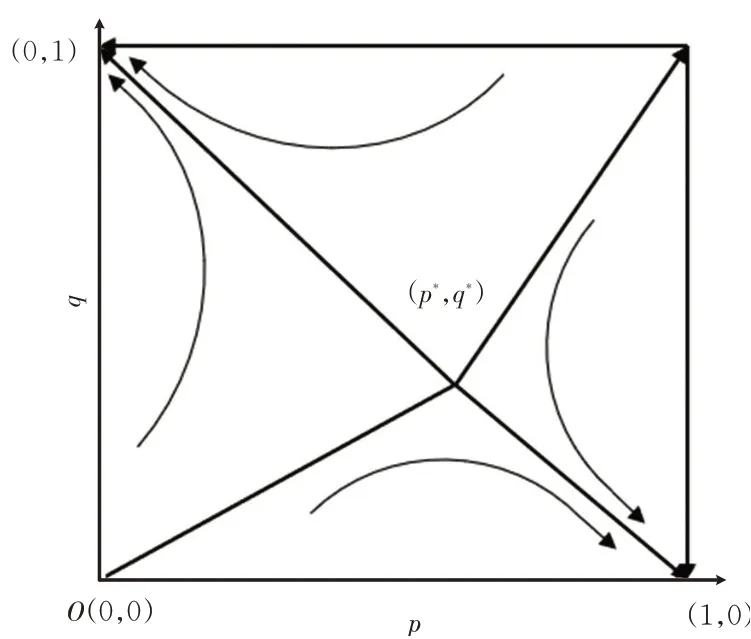
由表2可见:(0,0)和(1,1)是不稳定点,即行人和电动自行车都选择等待(减速)或者通行(穿越),这样会造成交通资源的浪费或者发生碰撞,造成危险。在(0,1)和(1,0)是稳定点,二者相互礼让,其中一方选择通行,在保证交通参与者通行安全的同时也使得交通资源得到较高程度的利用。
2.3 决策行为演化过程理论分析
在演化博弈模型的基础上,分析得到行人和电动自行车驾驶员的行为决策均衡点,明确行人和电动自行车的交通行为演化趋势以及演化策略的最终稳定点。
2.3.1 电动车过街行为选择的博弈演化趋势
对电动车的复制动态方程求导得
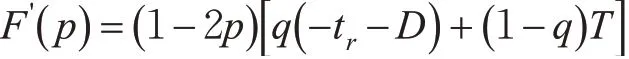
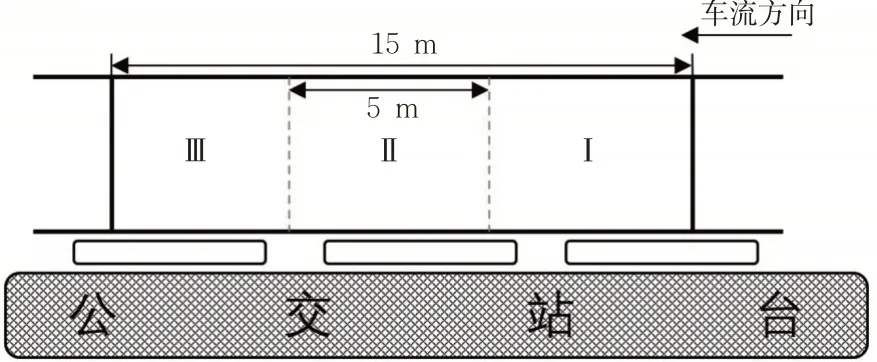
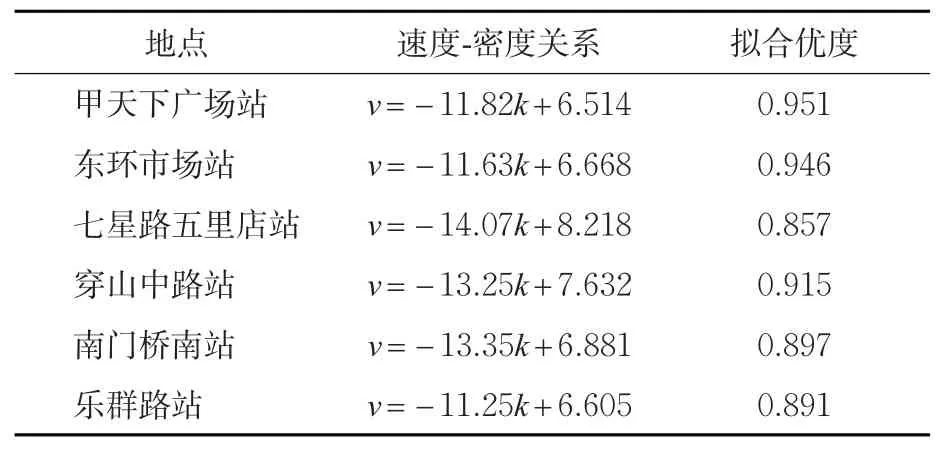
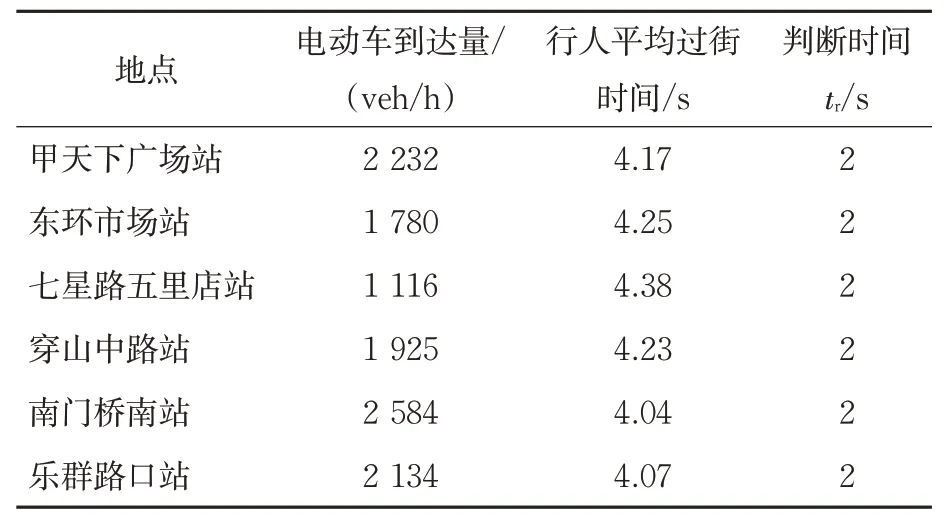
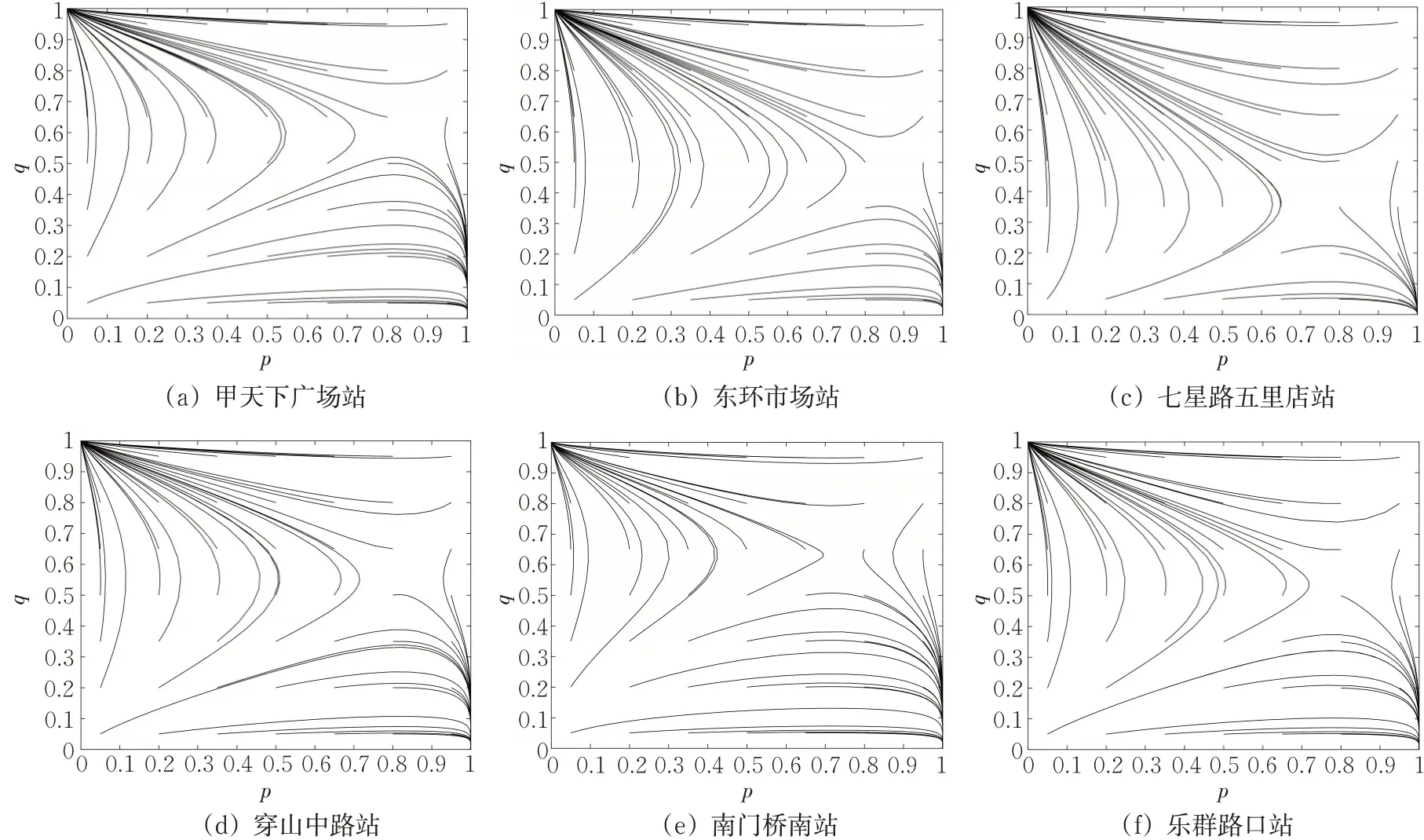
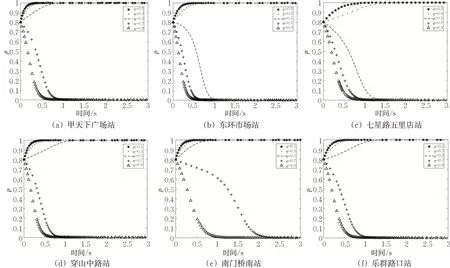
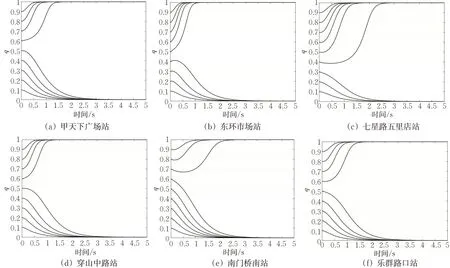
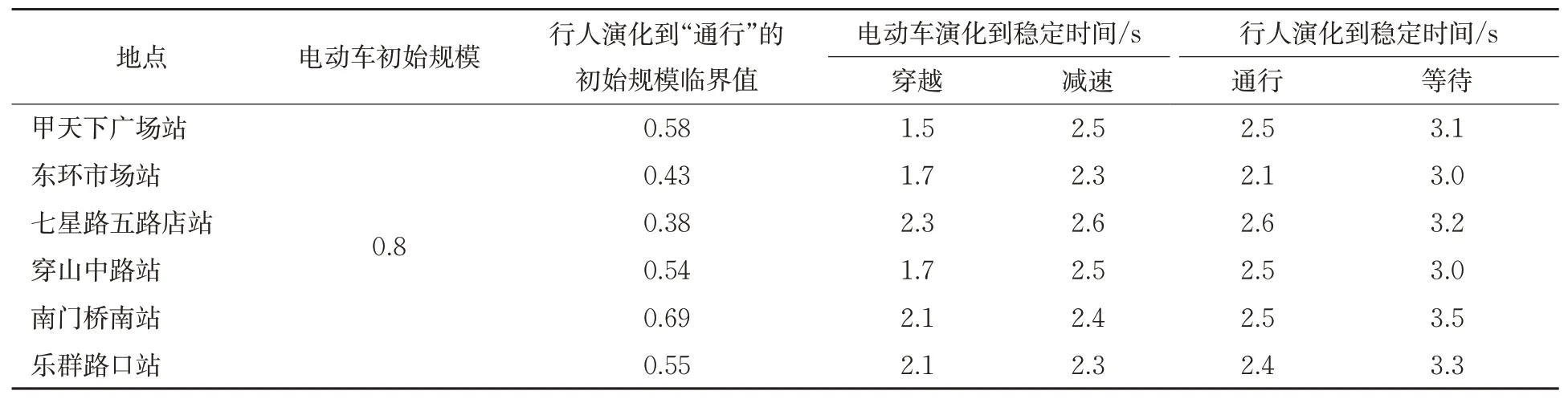
由实际意义可知q*的取值范围为0 2.3.2 行人过街行为选择的博弈演化趋势 对行人的复制动态方程求导得 根据实际意义得p*的取值范围是0 2.3.3 博弈双方的群体复制动态及稳定性分析 由2.3.2可见:行人和电动车的决策博弈过程展现了行人和电动车在冲突时选择不同通行策略的变化过程。在演化稳定点(0,1)和(1,0)处,演化过程体现了行人和电动车的通行策略为相互礼让;在动态演化过程中,鞍点(p*,q*)为行人和电动车演化的动态均衡点,表示在此场景中行人和电动车选择“通行”和“穿越”的规模。所以行人和电动自行车的通行策略演化过程示意图见图3。 图3 行人和电动自行车的演化过程示意图Fig.3 Schematic diagram of the evolution process of pedestrians and electric bicycles 研究地点选取桂林市甲天下广场站、东环市场站、七星路五里店站、穿山中路站、南门桥南站、乐群路口站,采集各站台区域电动自行车和过街行人通行数据。调查时间选取天气良好,环境能见度高,行人穿越非机动车道进出站台现象明显,存在饱和电动自行车交通流的高峰时段。调查地点的选取原则为设置有公交站台电动车交通量较大的城市主、次干道的非机动车道,具有物理机非隔离带,且路面平直。具体调查位置选取公交站台乘客进出通道偏向于车辆到达的方向,调查区域的非机动车道宽度为4 m,检测区域长度为15 m,并均分成3个长度均为5 m的区域,见图4。从上游开始,在行人和电动自行车发生冲突的区域中检测电动自行车在行人过街时采取的速度v2;当区间I中出现行人与非机动出现冲突时,则在区间Ⅲ中检测电动自行车在冲突结束后的采取的行驶速度v3;当区间Ⅱ中发生冲突时,在区间I中检测电动车在发生冲突之前的行驶速度v1。 图4 检测区域设置示意图Fig.4 Schematic diagram of detection area setting 调查方法为使用无人机,于合适的高度,垂直拍摄公交站台区域电动自行车和行人的交通视频。采用出入量法检测公交站区域行人和电动车交通流数据:以30 s为固定时间间隔统计电动自行车流量,以车辆前轮是否压线为标准判断其是否进入或离开检测区域;以通过检测区的电动自行车流量与通过检测区的平均速度的比做统计时间间隔内的交通流密度;以前后2辆电动自行车进入检测区域的时间差为车头时距,统计电动自行车群车头时距概率分布模型。以行人前脚踏入非机动车道为起始时刻,后脚离开非机动车道为终止时间,检测行人的过街时间。电动自行车交通流速度-密度拟合函数见表3。从表3可见:非电动自行车流的自由流速度为:v七>v穿>v南>v东>v乐>v甲。 表3 电动车流速度-密度拟合函数Tab.3 Velocity density fitting function of the electric bicycle flow 通过检测电动车群车头时距,进行概率统计分析,发现较好适用于指数分布概率密度函数。电动车到达量及行人过街平均时间见表4,判断时间取2 s,电动自行车加速度取值1.5 m/s2,减速度取值2.5 m/s2[19]。由表4可见:电动自行车的到达量为:λ南>λ甲>λ乐>λ穿>λ东>λ七。 表4 电动自行车和行人过街参数Tab.4 Traffic parameters of electric bicycles and pedestrians 根据以上实测数据对公交站区域的行人与电动自行车的通行选择策略演化过程进行仿真,演化图像见图5。 图5 公交站区域的行人与电动自行车选择策略演化Fig.5 Evolutionary selection strategies of pedestrians and electric bicycles in bus stop areas 根据问卷调查发现电动自行车驾驶员年龄处于18~50岁之间的比例为76%,在这个年龄段的驾驶员精力旺盛,在行驶过程中更倾向于选择“穿越”。因此,对于电动自行车群体,选取0.8作为群体中选取“穿越”策略的初始规模,电动自行车选择策略演化图像见图6。由图6可得以下结论。 图6 电动自行车选择策略演化Fig.6 Evolutionary selection strategy of electric bicycles 1)在过街行人的群体中采取“通行”决策的初始规模低于30%时,行人对交通环境安全性要求较高,此时电动自行车处于优势,选择策略稳定于“穿越”。随着行人群体中倾向于“通行”的初始规模上升,电动自行车的演化呈现出受到抑制的趋势。即行人群体选择“通行”策略比例的增大会增加行人过街的安全感。 2)电动自行车到达量越大,使电动自行车通行策略演化稳定于“减速”的行人初始规模临界值越大。表明电动自行车到达量越高,车流越稳定,越不容易被过街行人打断,即电动自行车到达量抑制行人“通行”策略的选择。 图7 为行人选择策略演化图像。由图7可得以下结论。 图7 行人选择策略演化Fig.7 Evolutionary selection strategies of pedestrians 1)从行人选择“通行”的初始规模临界值对行人通行策略的演化趋势的影响来看,电动自行车到达量越大,则行人选择“通行”策略的初始规模临界值也就越大。即电动自行车到达量的增大对行人选择“通行”策略具有抑制作用。电动自行车到达量减小时,个体间距增大,为行人过街提供更多机会。但此时电动自行车行驶速度快,若发生碰撞,危险性更大。即电动自行车到达量越小,越有利于行人过街,但对行人通行安全构成较大威胁。 2)行人选择“通行”的初始规模在临界值处时,曲线最初表现略微平直,表明行人对交通环境的安全性不够信任,决策过程表现出犹豫。对比发现,电动自行车自由流车速越高,行人犹豫现象越明显。这与实际中电动自行车以较大速度行驶,个体间空间较大,吸引行人穿越,但车辆间时距较小,行人无法完成过街过程而犹豫的情况相同。 电动自行车与行人通行策略演化到稳定状态最长用时及行人通行策略的演化稳定于“通行”的初始规模临界值见表5。 表5 电动自行车和行人的演化结果Tab.5 Evolution of electric bikes and pedestrians 由表5可见:不同检测地点电动自行车和行人在博弈过程中,电动自行车相比行人更快做出决策;二者通行策略演化结果稳定于“减速”或“等待”的时间较为均衡,电动自行车用时约2.5 s,行人用时约3.2 s;且通行策略稳定于“穿越”或“通行”的时间都短于通行策略稳定于“减速”或“等待”的时间,电动自行车平均用时减少约23%,行人平均用时减少约24%。表明交通参与者做出“通行”或“穿越”的决策较为果断,这与交通参与者快速做出决策把握机会通行的实际情况相符。 本文以公交站台区域为例,采用复制动态方程刻画群体之间的动态学习和信息反馈过程,建立基于时间延误的演化博弈模型,对城市共享交通环境中交通参与者发生冲突时交通行为的选择机理进行探究。 根据实例验证结果得出,选择“通行”的过街行人比例增大提升行人的过街安全感;电动自行车到达量较大时不利于行人过街,反之行人过街机会增多,但安全威胁较大;行人是否做出“通行”决策主要受电动自行车群车头时距影响;发生冲突时,电动自行车与行人做出“减速”或“等待”的决策时间较为均衡分别为2.5 s和3.2 s,且双方做出“穿越”或“通行”决策时间相比“减速”或“等待”的时间分别减少约23%和24%,能够反映交通参与者把握机会通行的实际情况。该演化博弈模型能够反映现实交通场景中行人与电动自行车之间冲突特点,在分析城市共享道路中交通参与者冲突行为特点有一定的通用性。 本文针对交通参与者选择不同行为的通行延误进行了量化,在下一步的研究中,可以对不同行为的选择产生的风险进行量化,以提高模型的精准性,更好地解释城市共享交通环境中行人与电动车冲突演化机理。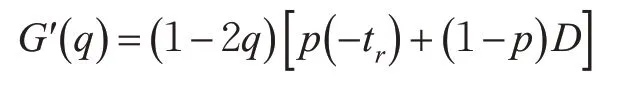
3 实例验证
3.1 模型参数标定
3.2 模型验证
4 结束语

