电涡流式TMD 减振设计方案探讨——以马尾天马山人行景观斜拉桥工程为例

■胡 灿

（福州市规划设计研究院集团有限公司，福州 350108）

为了提高行人和车辆的通行安全，实现人车分流，城市人行桥得以迅速发展。 同时随着对结构美学的不断追求，人行桥结构造型也逐渐轻巧、大跨、异形化。 近几年，国内外部分人行桥在使用过程中发生了大幅振动， 对行人舒适性产生了极大的影响。 但目前针对人行桥人致振动研究分析尚不够深入， 现行人行天桥规范仅规定天桥竖向固有频率＞3 Hz[1]，未对天桥人行舒适度计算分析做具体规定，所以当下需研究人行桥的振动原理，并根据相关原理进行动力设计[2-3]。 本研究以国内1 座全长514 m，主跨2 m×53 m 的人行景观斜拉桥为工程案例，对人行桥的人致振动原理、人群荷载的模拟及减振措施等进行计算和分析。

1 工程概况

马尾天马山天桥位于福州马尾经济技术开发区，主桥结构形式为独塔斜拉桥，采用空间异形索面；为了与马尾船政文化相结合，主塔采用轮船桅杆造型，寓意“扬帆起航”；平面采用圆曲线，展现出桥梁飘逸的造型， 天桥总长514 m， 主跨长度为2 m×53 m ，桥面宽4.5 m。 主桥塔柱、上部结构均为钢箱结构，墩身采用钢筋砼Y 型墩；主桥上部采用1.7 m 高钢箱梁，引桥采用0.9 m 高钢箱梁。 目前天桥除上跨福马铁路部分外，其余均已完工（图1）。

图1 主桥夜景

2 结构动力特性分析

类似车辆过桥产生涡合振动，行人过桥也会产生人与桥之间的相互作用。 目前有关人-桥动力相互作用的研究主要如下：（1）行人过桥对桥梁结构的自振频率的影响；（2）当行人较多时，后方行人会本能地调整步伐与前方一致；（3）当人群步频接近桥梁固有频率时，易发生共振[3]。

本研究采用有限元程序Midas/Civil 对天桥进行建模计算，计算方法采用多重Ritz 法进行迭代分析，结构整体模型见图2。

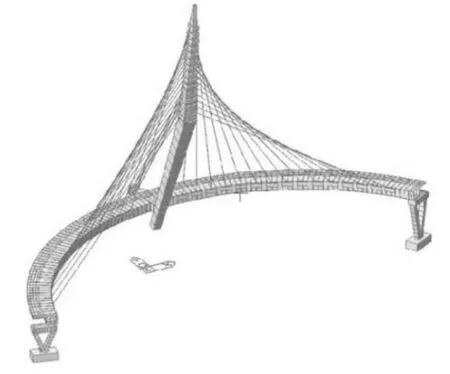
图2 主桥结构整体模型

经过对该结构模态分析计算结果可知，天桥各阶振型较为明确，其前六阶振型模态见图3～8，列取前10 阶振型的周期、频率及质量参数统计见表1。

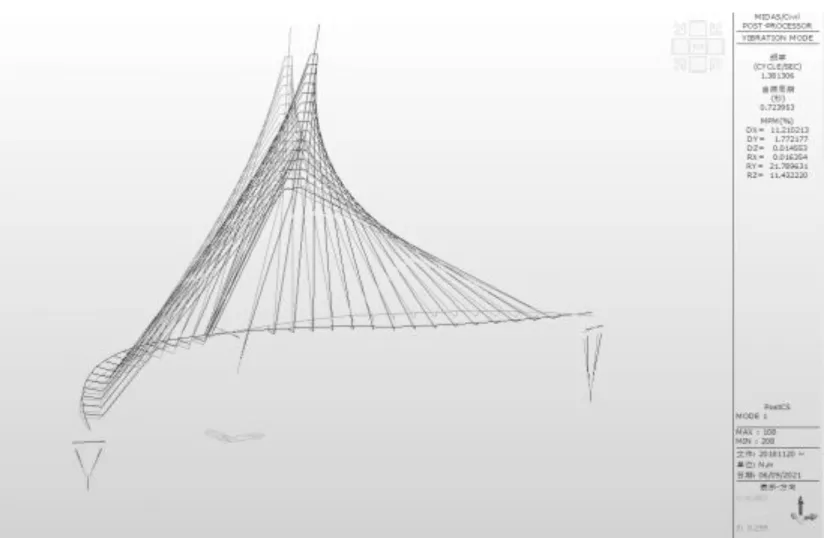
图3 一阶模态主桥振型频率1.38 Hz

图4 二阶模态主桥振型频率1.64 Hz

图5 三阶模态主桥振型频率1.74 Hz

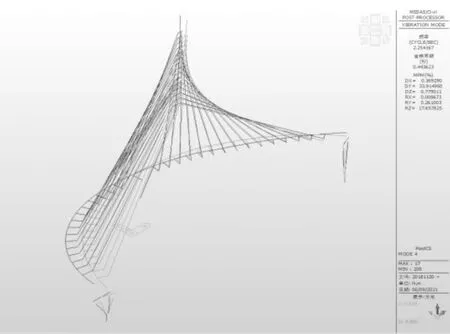
图6 四阶模态主桥振型频率2.25 Hz

图8 六阶模态主桥振型频率3.38 Hz

由表1 可知， 该结构竖向1 阶振型的频率为1.38 Hz， 由于行人的常规步行频率为1.5～3.2 Hz；所以当多人进行有规律的步调行走时，天桥易产生共振，同时结合软件计算分析发现在天桥跨中位置确实会发生较大的加速度。

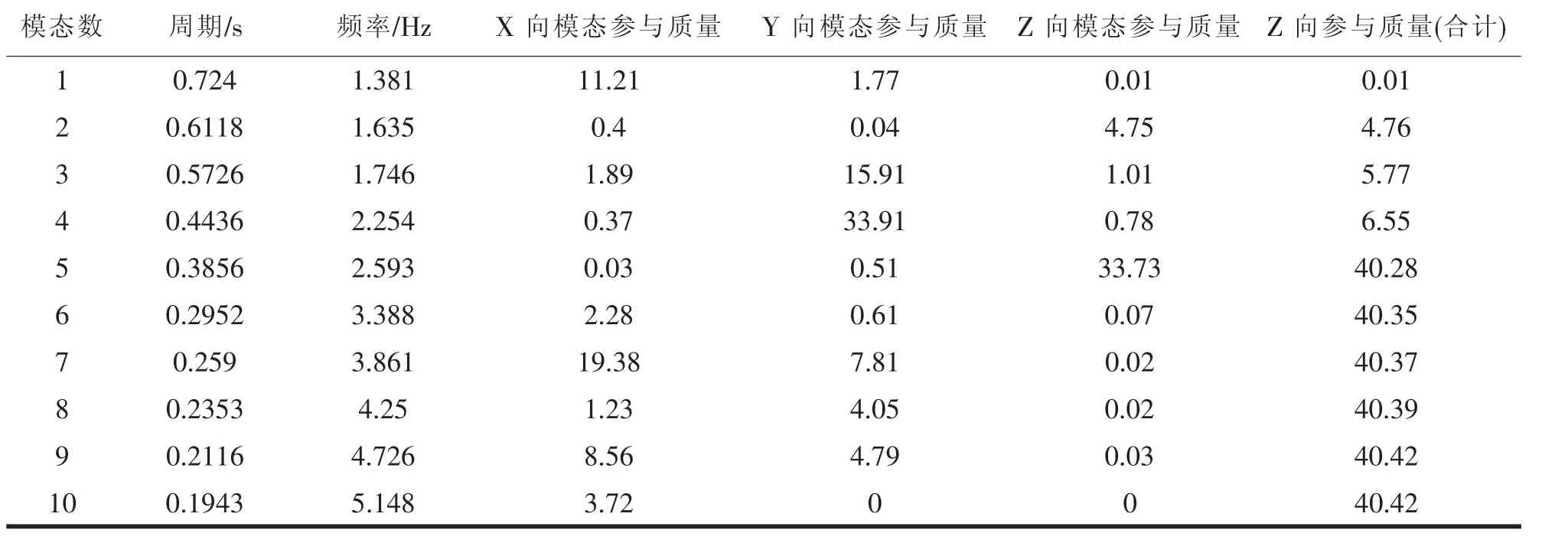
表1 前10 阶振型周期及其参与质量

由于现代高强材料的应用，天桥结构一般不会发生强度破坏； 但是会产生由共振引起的巨大振幅，该振幅容易超过人所能承受的极限；特别对于大跨度的索结构、 低梁高等结构刚度较小的桥梁，由于其自身柔性结构特性， 极易产生受迫振动；同时该桥梁高已增至1.7 m， 考虑本桥极高的景观需求， 若梁高继续增大势必会降低结构造型的美感，以及造成材料浪费， 所以本桥需进行消能减振设计。 目前，相关技术已在国内外应用于一些工程实践中，同时结构消能减振已作为《建筑抗震设计规范》[4]一种重点推荐技术。

3 消能减振原理

调频质量阻尼器（TMD）是一种减振消能装置，由主结构和子结构组成。 调整结构参数，可使子结构具有与主结构相近的频率。 当主结构受外荷载激励产生振动， 子结构会受迫产生与之相反的惯性力，从而达到削弱主结构的振幅的目的。 TMD 自振频率主要由以下几个参数控制： 减振器的有效刚度kd，可通过调整弹簧直径、有效长度等参数改变；系统阻尼Cd由阻尼器决定，其值及调频质量md的大小均由计算得出[5]。 图9 是等效的单质点结构受激励的TMD 减振示意图。

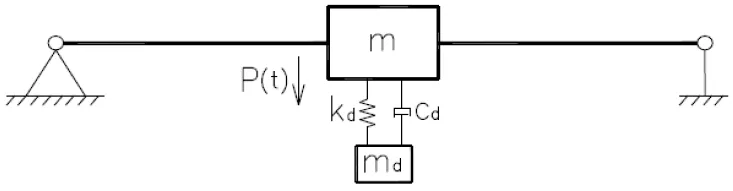
图9 TMD 减振系统示意图

4 荷载模拟

4.1 单人人行荷载模拟

单人步行激励曲线竖向荷载模型参照《德国人行桥设计指南》[6]均布谐波荷载pv(t)[N/m2]计算，如式（1）。

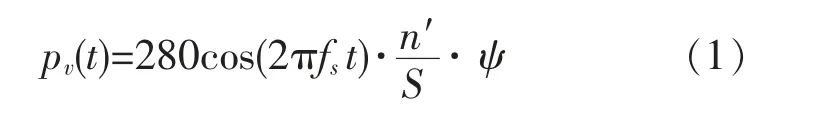
式中：fs——所分析竖弯模态的频率(Hz)；

n′——加载面积S 内行人流等效人数(个)；

S——加载面积（m2)；

ψ——考虑步频接近基频变化范围临界值的概率而引进的折减系数，按图10 取值。

图10 折减系数（竖向）

根据上述公式计算的单人荷载时程曲线见图11。

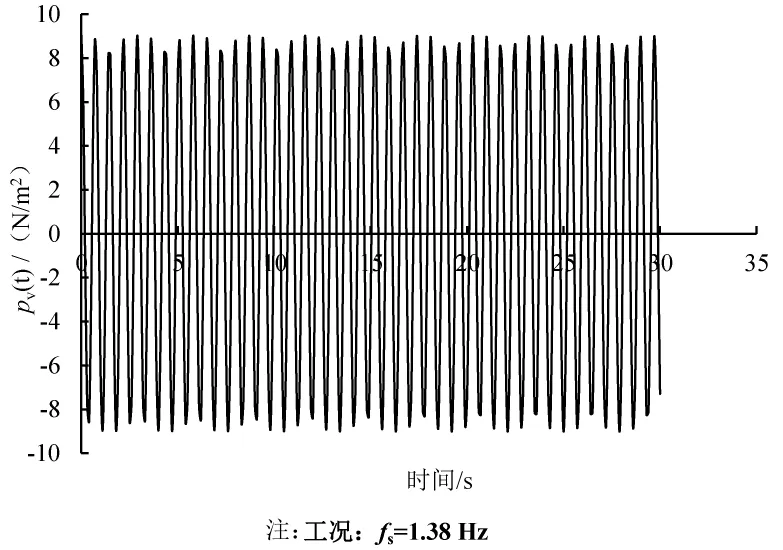
图11 行人荷载样条曲线

4.2 人群荷载模拟

目前人群步行荷载的模拟是将单人步行荷载进行组合得到。 由于行人步调不同，相互抵消等原因，所以人数为n 的人群可等效为n′个步调一致的行人荷载，ps为同步概率：

式中：n 为人群总数；d 为行人密度， 本研究参照《德国人行桥设计指南》[6]采用交通异常繁忙的人行交通级别:d=1.5P/m2。

4.2.1 低密度人群行走

4.2.3 步行荷载的加载

步行荷载的加载方向应根据计算结构振型，按照使结构产生振动最不利的方式加载，见图12。

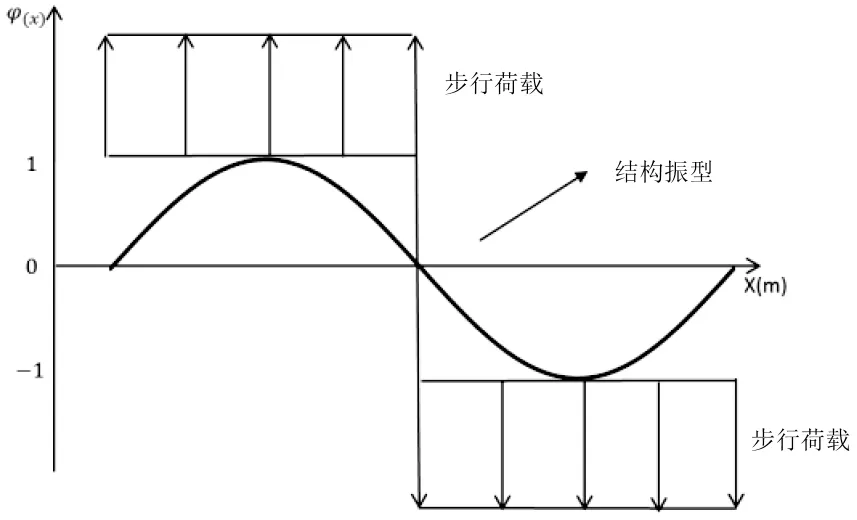
图12 步行荷载根据振型φ(x)加载

5 消能减振方案

5.1 结构振动分析

根据上述人群荷载工况， 并应用模拟的荷载曲线，进行人行荷载激励下的动力响应分析,假定前30 s 天桥受人群发生强迫振动，后10 s 取消荷载自由振动。 计算发现在人行激励下，天桥跨中竖向加速度时程曲线如图13 所示， 加速度峰值为1.206 m/s2,根据《德国人行桥设计指南》[6]舒适性级别（表2）可知，天桥的舒适性较差；所以应进行消能减振设计。

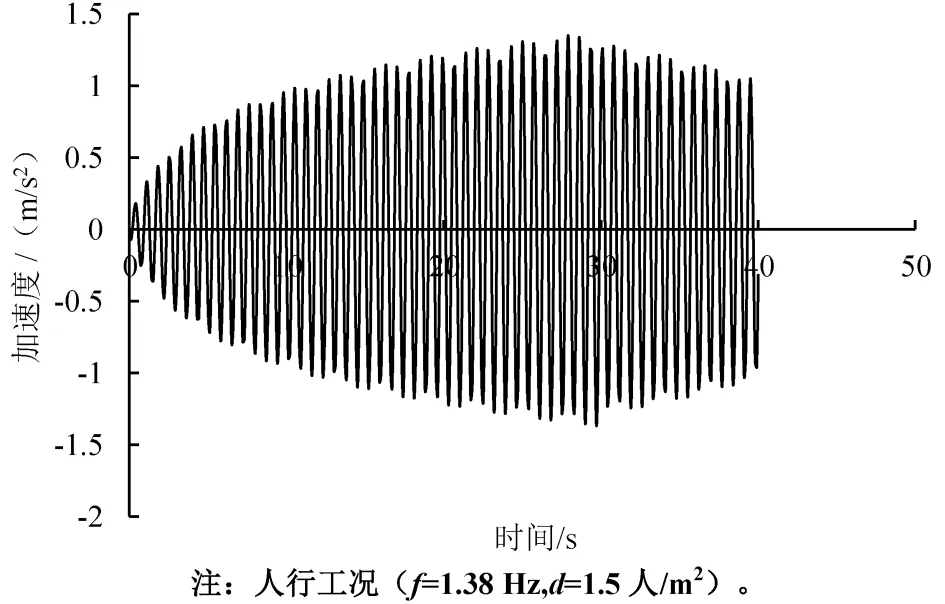
图13 天桥跨中竖向加速度时程曲线（未设置TMD）

表2 舒适级别（通过加速度确定）

5.2 TMD 布置方案设计

根据对本天桥的动力计算分析可知，需要对其采用专项消能减振设计， 拟采用电涡流式TMD 消能减震系统。相比普通TMD，电涡流式TMD 具备更加优越的减振性能[8]，本方案以电涡流式TMD 的性能参数进行计算、分析、优化。

经过对计算结果的优化分析，在天桥振幅较大的位置布置电涡流式TMD 减振装置 （图中用方块表示， 一个方块表示四套电涡流式TMD， 总共16套），布置图如图14 所示，阻尼器的梁体布置图见图15；表3 中的减振装置参数为多次计算研究及不断调整得到。

表3 减振系统计算参数

图14 电涡流式TMD 布置示意图

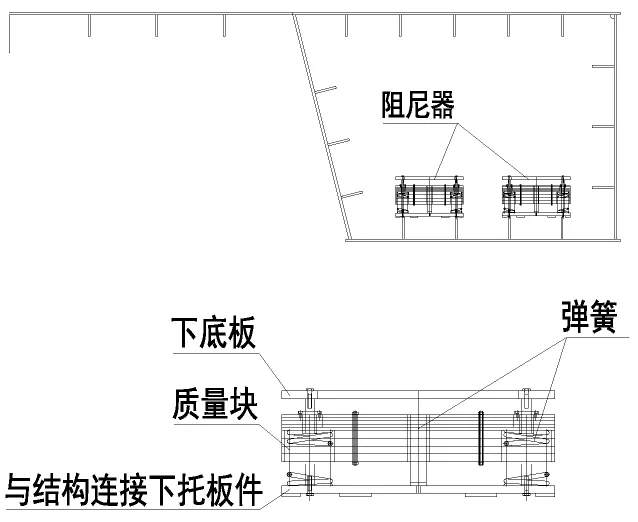
图15 阻尼器示意与主梁梁内布置图

5.3 减振结果分析

根据上文的定义的人群工况、荷载曲线，天桥跨中竖向加速度时程曲线见图16， 加速度峰值为0.174 m/s2，对比计算设置阻尼器前后的跨中加速度峰值如表4 所示。

表4 人行工况作用下天桥计算加速度峰值

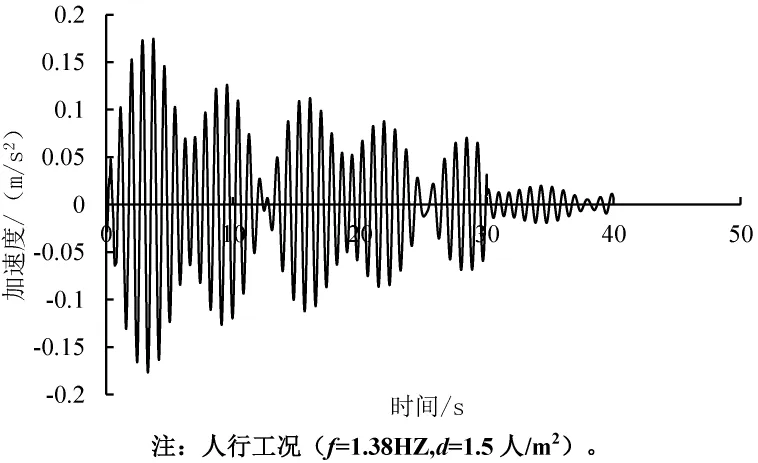
图16 最大响应处加速度时程曲线对比

6 结语

本研究对天桥结构在一阶竖向振动工况下进行了设置电涡流式TMD 的减振设计与分析， 通过结构动力分析及多次计算， 提出该天桥包含合适参数的TMD 布置方案。 结果表明，通过在结构振幅最大位置设置电涡流式TMD 可以有效降低天桥在人行激励作用下的产生的振动：（1）对于本天桥，当步行频率为1.38 Hz 时，天桥跨中加速度峰值最大达到1.206 m/s2；行人舒适性较差，故需对该结构进行减振设计；（2）按本研究所设计的减振方案，采用行人同步荷载模型（步行频率为1.38 Hz）：减振后天桥的最大加速度峰值为0.174 m/s2， 最大减振率为85.6%，符合《德国人行桥设计指南》[6]要求，表明该减振设计方案可以有效改善该人行桥的舒适性；（3）最后根据本桥现场TMD 监测调试结果可知，设置TMD 后天桥实测峰值加速度与计算结果接近，满足设计要求。