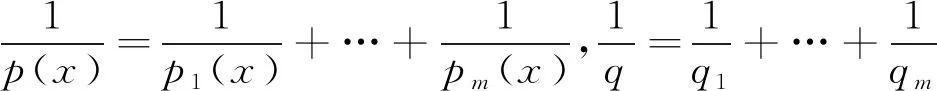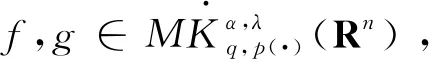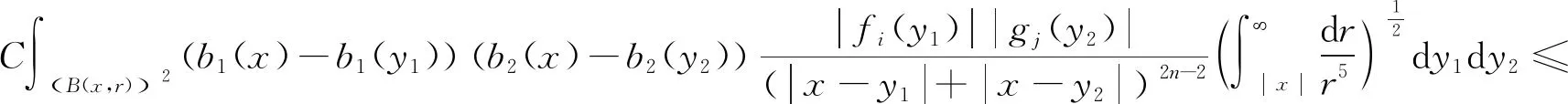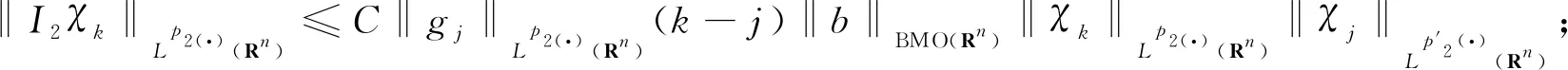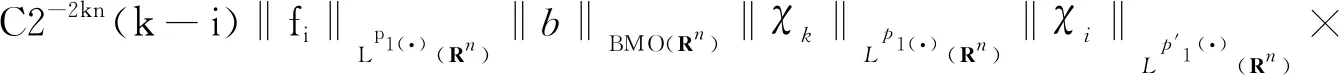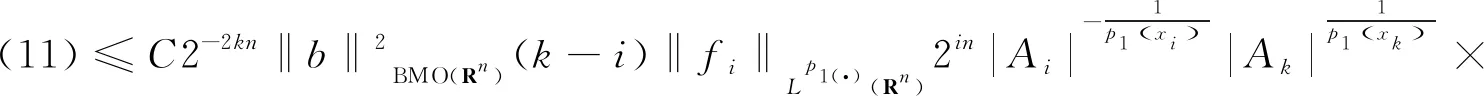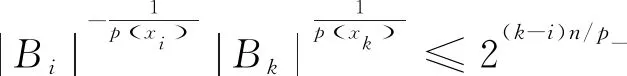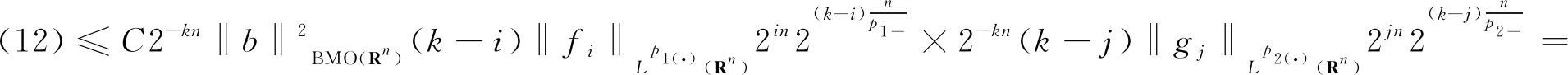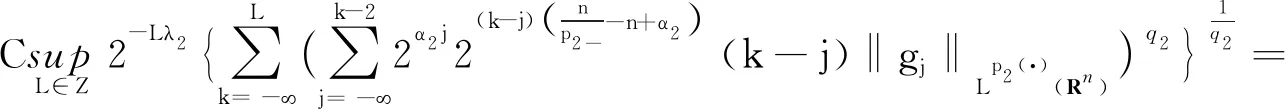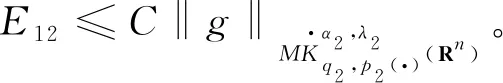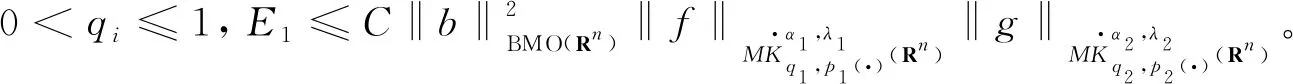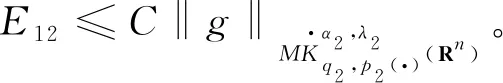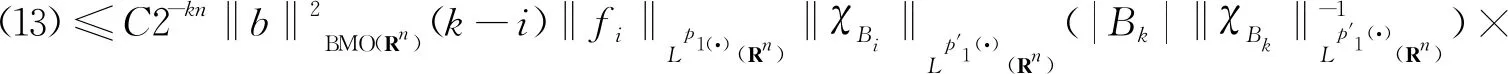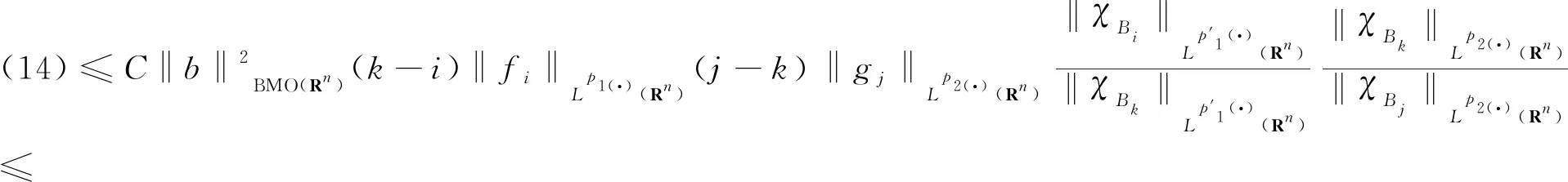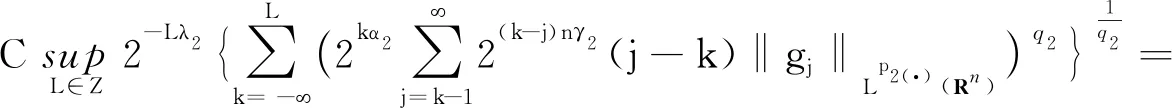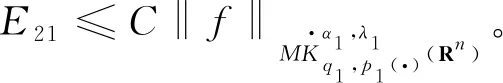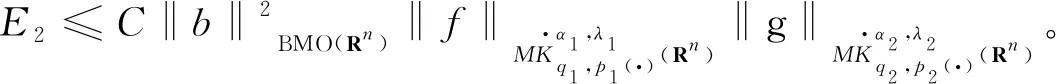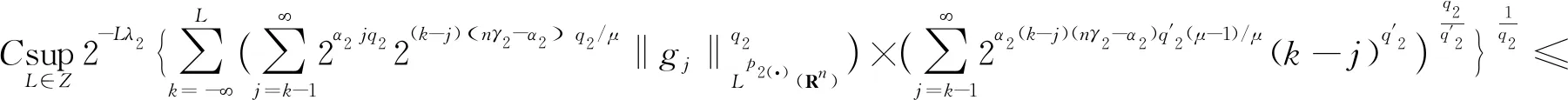多线性Marcinkiewicz高阶交换子在变指数Herz-Morrey空间上的有界性
韩 晶,叶晓峰
(华东交通大学 理学院,江西 南昌 330013)
0 引言
各类算子在不同空间上的有界性刻画一直是调和分析的主要问题。当算子的核函数满足不同条件时,算子的性质也就不同。文献[1]研究了带变量核的Marcinkiewicz算子的有界性。文献[2]研究了带奇变量核的Marcinkiewicz算子的有界性。文献[3]研究了带粗糙核的Marcinkiewicz算子的有界性。文献[4]研究了当粗糙核Ω满足零阶齐次函数和Ω∈Lipα(Sn-1)(0<1≤α)时,Marcinkiewicz型积分算子及其交换子在变指数Herz-Morrey空间上的有界性。以上文献仅仅研究了当核函数满足一定条件时,线性算子及其交换子的有界性。文献[5]研究了Marcinkiewicz高阶交换子在变指数Herz-Morrey空间上的有界性。文献[6]证明了多线性奇异积分算子与有界平均振动(bounded mean oscillation, BMO)函数生成的交换子在变指数Herz-Morrey 空间上的有界性。基于以上研究,本文研究并确定了当核函数满足一定条件时,多线性Marcinkiewicz算子与BMO函数生成的高阶交换子在变指数Herz-Morrey空间上的有界性。
1975年,文献[7]开始了对多线性算子的研究,并给出多线性算子的定义:
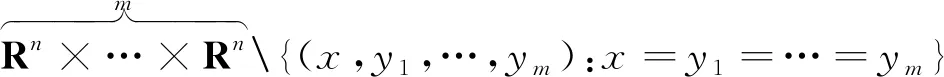
假设核函数K满足下面的尺寸条件,即对所有的x,y1,…,ym∈Rn,只要存在1≤j≤m,满足x≠yj,有
以及核函数K满足正定性条件,即存在常数δ∈(m,+),对每个正数M满足2|x-x′| 其中,b为BMO函数,定义如下: 设b∈Lloc(Rn),若b的平均振动是有界的,即M#b∈L,则称b为BMO函数,其全体记作BMO(Rn),称为BMO函数空间,简记为BMO。 设B(x,r)={y∈Rn:|x-y| 定义1[9]设p(·):E→[1,)是一个可测函数。 (Ⅰ)变指数Lebesgue空间Lp(·)(E)定义为: Lp(·)(E)={f可测ρp(f/λ)<对某些常数λ成立},其中 定义 p-=ess inf {p(x):x∈E},p+=ess sup {p(x):x∈E}。 集合P(Rn)表示由所有满足1 (Ⅲ)设α∈R,0 其中,范数表示为: 引理1[10]当0 (1) 引理2[11]如果p(·)∈P(Rn),存在一个常数C>0,且对于所有球B在Rn中,下面不等式成立: (2) 引理3[10]如果p(·)∈P(Rn),存在常数0<γ<1和C>0,对任意的球B⊂Rn和任意的可测子集S⊂B,有下面的不等式成立 (3) A=B(0,r)B(0,r/2)。如果|A|≥2-n,则有 ‖χA‖p(·)≈|A|1/p(x), (4) 这里隐含常数不依赖r且x∈R。 (5) 其中: 设E是Rn中的开集,如果p(·)∈P(Rn),且满足下面两个条件: (6) (7) 则有p(·)∈B(Rn)。 引理7[15]如果b∈BMO(Rn),m∈N,i,j∈Z满足i (8) (9) 定理1设p(·)∈P(E),p(·)满足引理6中的式(6)和式(7),其中 当m=2时, 根据变指数Herz-Morrey空间的定义 由于E2和E3对称,则只要分析E1,E2,E4即可。根据核函数K满足尺寸条件和Minkowskiw不等式, B1+B2。 由中值定理可得: (10) 由E1注意到i≤k-2,j≤k-2,且|x-y1|~|x|~2k,|x-y2|~|x|~2k,其中x∈Ak,y1∈Ai,y2∈Aj。则根据引理5、中值定理和式(10)可得: 则‖[b1,b2,μ](fi,gj)(x)χk‖Lp(·)(Rn)≤C2-2kn‖I1χk‖Lp1(·)(Rn)‖I2χk‖Lp2(·)(Rn)。先分析‖I1χk‖Lp1(·)(Rn): 则根据引理7,可得: 再分析‖I2χk‖Lp2(·)(Rn),同‖I1χk‖Lp1(·)(Rn)分析一样,可得: (11) 由引理4,可得: (12) 可得: 当0 当1 当1 由E2可注意到i≤k-2,j≥k-1,且|x-y1|~|x|~2k,|x-y2|~|max{|x|,|y2|}|~max{2j,2k},其中x∈Ak,y1∈Ai,y2∈Aj。当j≥k-1,有两种情况:当k>j时,B1,B2和E1中的B1,B2得到的结果一样;当k b2(y2)gj(y2)dy2=C2-kn2-jnI1I2。 ‖[b1,b2,μ](fi,gj)(x)χk‖Lp(·)(Rn)≤C2-kn2-jn‖I1χk‖Lp1(·)(Rn)‖I2χk‖Lp2(·)(Rn)。 分析‖I1χk‖Lp1(·)(Rn),‖I2χk‖Lp2(·)(Rn)和E1中的‖I1χk‖Lp1(·)(Rn),‖I2χk‖Lp2(·)(Rn)一样,可得: 注意到:‖χi‖Lp(·)(Rn)≤‖χBi‖Lp(·)(Rn),最后可得: ‖[b1,b2,μ](fi,gj)(x)χk‖Lp(·)(Rn)≤C2-kn‖b‖2BMO(Rn)(k-i)‖fi‖Lp1(·)(Rn)‖χBk‖Lp1(·)(Rn)× (13) 由引理2,可得: (14) 由引理3,可得: ‖b‖2BMO(Rn)C2(i-k)nγ1(k-i)2(k-j)nγ2×(j-k)‖fi‖Lp1(·)(Rn)‖gj‖Lp2(·)(Rn)。 当1 E223与E221的形式一样,E224与E222的形式一样,则用同样的方法估计不等式可得: 当1 由E4可注意到i>k-1,j>k-1。分下面4种情况:当i 与E2中‖[b1,b2,μ](fi,gj)(x)χk‖Lp(·)(Rn)的方法相同,可得: ‖[b1,b2,μ](fi,gj)(x)χk‖Lp(·)(Rn)≤ C‖b‖2BMO(Rn)2(i-k)nγ1(i-k)2(k-j)nγ2(j-k)‖fi‖Lp1(·)(Rn)‖gj‖Lp2(·)(Rn)。 可得: E41和E42的形式与E22的形式一样,可得: 定理1证毕。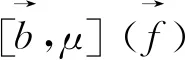
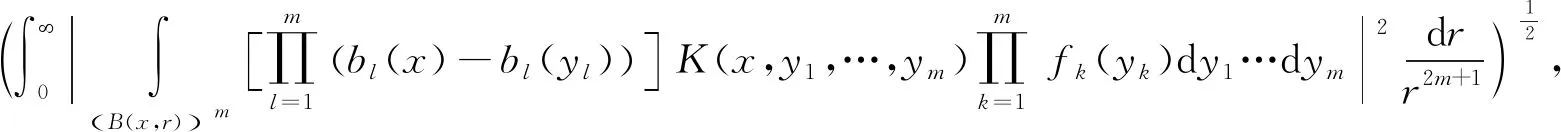
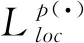
1 引理
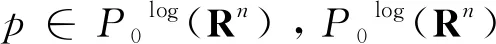

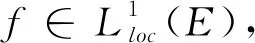
2 主要结果