驾驶员变更车道对信号交叉口交通流的影响

成 卫，周 通，李 冰

(昆明理工大学 交通工程学院，云南 昆明 650500)

0 引 言

随着城市经济的发展，交通问题引起了人们的极大关注.交叉口是城市道路网的重要组成部分，对道路通行能力会产生很大的影响.机非混合的交通环境使交通出行更加复杂，驾驶员在驾驶过程中需要考虑不同车辆的影响.例如，驾驶员可以通过变更车道来实现较好的行驶环境.现有研究主要通过交叉口渠化、通行能力设计、信号配时优化以及交通运行状态评估等方面来改善道路的运行条件，并为城市规划建设提供数据基础.近年来，共享自行车模式的快速发展使机非混合交通特性更加凸显，研究混合交通环境下驾驶员变更车道对交叉口交通流的影响，分析交叉口的交通事故与驾驶行为的内在联系，具有重要的实际意义.元胞自动机(cellular automaton)模型具有离散型、复杂性等特点[1]，利用元胞自动机建立模型是研究交叉口混合交通流一种较好的方法.李文兵[2]针对车辆行驶中的安全因素,考虑到了静止车辆和低速车辆,在一维对称双车道元胞自动机模型的基础上，建立了一种新的对称双车道元胞自动机模型，给出了计算机数值模拟的新模型流量—密度图、时空斑图以及车道改变率—密度图；2012年曲仕茹[3]在一定的约束条件下，根据驾驶员的行为特性，研究了驾驶员行为特性对通行能力的影响，却缺少了驾驶员换道特性研究；2014年梅超群[4]分析了驾驶员属性对于交通流的影响，模型中也考虑到了驾驶员特性，在相同驾驶环境下，性别和年龄是影响换道行为的重要因素.而利用元胞自动机建立驾驶员变更车道模型，研究混合交通环境下驾驶员变更车道对交叉口交通流影响的还相对较少.本文基于元胞自动机模型，通过分析混合交通环境下的交通流特性与平均车速的变化，来研究换道行为对信号交叉口通行能力的影响.

1 车辆变道模型的建立

1.1 模型的建立

建立基于元胞自动机城市道路路段模型，假设车辆为了有更好的行驶环境，在保证安全的可视距离之内驾驶员可以变更车道.模拟一条长度L=800 m的道路，把车道划分为不同的单元格.驾驶员在进入交叉口时可观察到交叉口信号灯的距离R=180 m，交叉口进口到出口大约为26 m.根据城市道路的行车规则，机动车最大行车速度应该为40 km/h，而在这个速度行驶的条件下，驾驶员最大的安全视距为180 m.模型对三个车道的模拟过程和其他多车道交通流模型一样[5]，驾驶员可以在道路条件良好的情况下自由变更车道.模拟车辆行驶规则如图1所示.

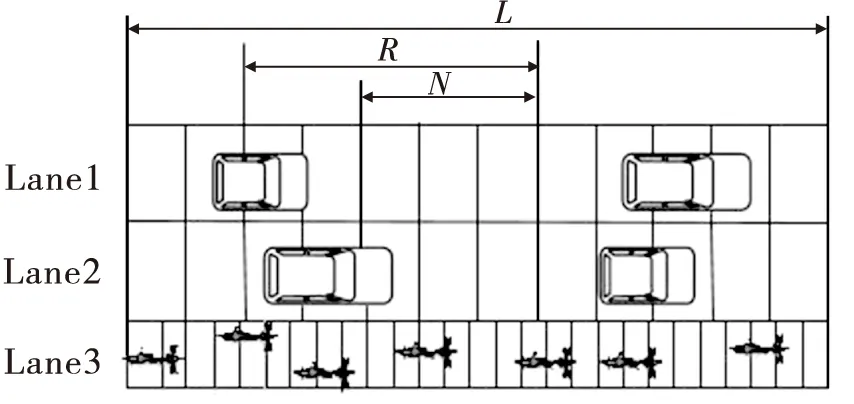
图1 换道规则Fig.1 Lane change rule

1.2 模型参数的标定

建立基于元胞自动机城市道路路段模型，每条车道的长度为800 m，车道的横向宽度为3.75 m，每个元胞格大小为1.25 m×1.25 m，每条车道被纵向分为640个单元格，横向车道划分为8个格子，机动车一般占用3个单元格，非机动车占用1个单元格.按照车辆行驶方向，车道从左至右分别为第一车道、第二车道和第三车道，车道编号依次为Lane1、Lane2和Lane3.考虑不同车型的车辆换道规则不一样，所以对通行条件和安全条件的要求也有所区别.vs(t)、xs(t)和ds(t)分别表示第s辆车在t时刻的速度、位置和与其邻近前车的距离；其中ds(t)=xs(t)-xs+1(t)-ls+1，ls+1代表对应前车s+1的长度[5].假设所有机动车的最大行驶速度vmax为40 km/h.

把道路的驾驶员分为三种类型：冲动型(a)、稳重型(b)和胆小型(c)，他们对应的概率分别为Pa、Pb、Pc，而且满足约束条件:

Pa+Pb+Pc=1

(1)

在相邻车道道路条件良好，信号灯可视范围内，一般情况下Pa>Pb>Pc.

1.3 换道规则

建立的模型对三个车道的模拟过程和其他模型的模拟过程也是相似的[6].驾驶员的变道条件取决于目标车道与本车道的驾驶条件，在条件良好的情况下，最后不同的车辆换入各自的目标车道.汽车在道路上行驶时，道路的每一条车道行驶的交通条件都是随着时间的变化而变化的，而每个驾驶员都想在行驶环境好的车道行驶，因此驾驶员在行驶过程中会经常变更车道来满足自己的行驶需求[7-8].城市道路交叉口的交通环境比较复杂，特别是在机动车和非机动车混合交通的情况下，车辆在变更车道时会受到很多因素的影响.考虑自己行驶车道的同时，还要考虑到目标车道的交通条件，要确保变更车道后不会给本车道和目标车道带来安全事故.不同的车辆受限于车型结构等因素，车辆的运行规则也不同.相对于机动车而言，非机动车行驶时具有随机性和复杂性，行驶安全性也更小[9].由于城市道路车辆换道过程的随机性，加剧了城市道路交叉口交通流的不稳定性，所以分别给出两条机动车道上不同车型的换道规则[10].

车辆换道规则:当第s辆车从1车道换入到2车道，或者是从2车道换入到1车道应该满足下面的条件：

1)驾驶员变更车道的过程中，当本车道行驶条件不理想，而目标车道的行车环境更加良好，就可以选择变更车道，应该满足一定的安全条件：

(2)

xs(t)≤L-50

(3)

(4)

道路环境随着时间的变化而变化，驾驶员的驾驶行为也不同.因此，在建立模型时需要加入一个控制参数β来提高模型的准确性.考虑车辆在城市道路的平均运行速度为40 km/h,车辆类型的不同，控制参数也会随着改变，根据实际的交通情况，机动车控制参数βmax为4，非机动车控制参数βmin为2[11].

2)驾驶员换入目标车道Lane2需要的安全条件:驾驶员自由变更到目标车道后，驾驶员需要保证前后相邻的车辆正常行驶过程中不会发生碰撞.在这个模型中，车辆类型不同，其减速规则也是不一样的.因此，在设置车辆行驶的安全条件时，一般满足的条件都是后车在安全视距内，车辆在制动过程中不与前车发生相撞.运动方程描述如下:

(5)

(6)

式中：dno代表非机动车与机动车初始的距离，dbo代表机动车前后车之间初始的距离，m表示机动车的减速能力，mn表示非机动车的减速能力，vn代表非机动车车速，v为机动车车速，D为模型的修正参数.根据文献[12]可得修正参数如表1所示.

表1 模型修正参数

1.4 更新规则

1)确定慢化函数：

(7)

式中：bs是车辆s的刹车状态，bs=1(0)表示第s辆刹车灯亮(灭)，如果vs>0则ts=ds/vs；否则，th=0,ts=minv(s,h)，h表示驾驶员看到刹车灯的作用范围，Pb表示车辆可以减速的概率，Po表示车辆可以加速的概率.

2)安全加减速:

(8)

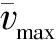
3)元胞位置更新：

xs(t+1)=xs(t)+vs(t+1)

(9)

2 模型仿真实验分析

本次实验运用MATLAB软件进行仿真，模拟实验中获取交通密度、平均车速、可视范围R、车辆延误等参数，分析驾驶员变更车道对信号交叉口交通流的影响[13].模型每次运行6×103次(约合1 h)，为了减小试验开始阶段的误差，选取了模型运行较为稳定时的数据进行分析，即当模型运行到3×103以后的数据进行分析.

2.1 交叉口信号控制参数设置

模拟一个道路交叉口，驾驶员在可视距离内可以变更车道，设置交叉口绿灯时长为50 s，黄灯清空时间为3 s，交叉口总的周期时长设置为100 s.通过改变交叉口的绿信比，获取车辆一定周期内的车辆平均车速、道路交通密度和车辆延误等参数，并对这些数据进行分析[14-15].

(10)

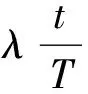
2.2 交叉口交通流基本图分析

2.2.1 可视范围内变更车道与延误的关系

从图2我们可以看出，冲动型驾驶员在可视距离内的延误6.038≪∂≪5.874.因为这一类的驾驶员可能对速度要求十分的高，在可视距离内，相邻车道行车条件良好，变更车道会影响车道上其他车流.在可视距离为80 m的时候出现了较大的波动，因为延误会随着可视距离的变化产生一定的变化；胆小型驾驶员在可视距离内的道路延误5.458≪∂≪2.486，这一类驾驶员为了保证行车的安全性，即使在可视距离较大的情况下，也不变更车道.所以，在可视距离范围内驾驶员类型对交通流影响比较明显：冲动型驾驶员会导致目标车道的车辆行驶受到比较大的干扰，道路上冲动型驾驶员增多会降低交通疏散的效率；胆小型驾驶员跟车较为稳定，整个路段车辆的平均车速一直在增加，在交叉口绿灯放行的阶段会增加道路的通行效率.

图2 可视距离内的车辆延误Fig.2 Vehicle delays within visual distance

2.2.2 交叉口流量与密度的关系

从图3流量与密度图可以看出：冲动型驾驶员行驶过程中，道路密度为0.223≪ρ≪0.612，因为这一类的驾驶员在可视距离内，行驶速度可能比较快，所以道路上车辆的密度较小，而在交通流量为0.135的时候密度最大，此时的交通运行状态最好；胆小型驾驶员驾驶过程中，道路密度大概为0.296≪ρ≪0.667，这一类驾驶员为了避免交通事故而选择较小的行车速度，跟车距离也比较稳定，道路的占有率也比较大，因此会出现道路的车流量小而道路密度可能会比较大的情况.

图3 交通流量与密度的关系Fig.3 Relationship between traffic flow and density

2.2.3 绿信比的变化对交叉口影响分析

从图4、图5可以看出：在不同绿信比条件下，驾驶员变更车道对信号交叉口交通流产生的影响不同，交叉口的交通密度变化的范围0.128≥ρ≥0.172辆/m，平均车速变化的范围为22≤v≤45 km/h.通过数据分析可知，绿信比对道路交通流的影响很大，冲动型驾驶员在绿信比较大的情况下换道，车辆延误的时间较小，而在绿信比较小的情况下换道则延误时间会增大；稳重型驾驶员对交通流的稳定性影响比较小，更有利于车辆通行；胆小型驾驶员在不同绿信比条件下平均车速变化较大，车辆延误时间也较高，这类驾驶员的跟车较为稳定，此时交叉口绿灯时车队的运行速度整体会变慢，不利于交叉口绿灯时间和黄灯清空时间的通行，而对于车辆排队等候是有利的.

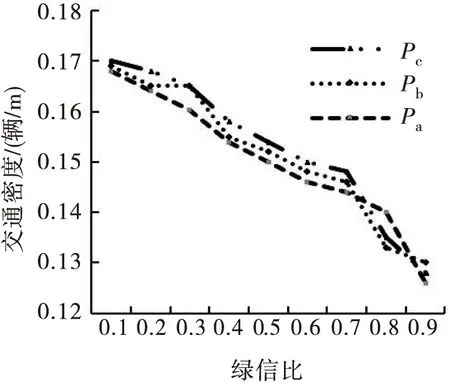
图4 不同绿信比下的交通密度Fig.4 Traffic density at different splits

图5 不同绿信比下的平均车速Fig.5 Average vehicle speed at different splits

从表2的对比分析我们可以看到，当可视距离为90 m的时候，两类驾驶员车辆的延误减少了1.9 s.当交叉口的绿信比为0.6时，两类驾驶员车辆的平均车速差距为8 km/h，说明交叉口绿信比超过一定数值时，驾驶员变更车道对交叉口的通行效率影响不显著.

表2 不同类型驾驶员结果分析对比

3 结 论

1)本文采用MATLAB进行仿真，提高了模型的准确度，模拟实验获取了车辆平均车速、道路交通密度和可视范围内的车辆延误时间等参数，通过数据分析阐述了驾驶员变更车道对交通流的影响.实验数据表明：驾驶员变更车道会对交叉口的交通流产生影响，驾驶员特性也是我们不能忽视的一个因素.当可视距离较长时，冲动型驾驶员车辆延误的时间减小了4.6%，可视距离较短时车辆的延误时间增大了2.8%，说明冲动型驾驶员的延误会随着可视距离R的变小而增大，非常不利于绿灯时交叉口的通行；胆小型驾驶员在可视距离较长时车辆的平均车速增大5.9%，车辆延误时间减小了2.3%，说明这类驾驶员在交叉口更有利于绿灯时间内车辆的通行.在信号控制交叉口，道路上的交通密度随着绿信比的增大而减小，当交叉口的绿信比A≥0.7的时候，道路交通密度会减小0.04，车辆的平均车速会增大3 km/h，车辆的延误减小了1.25 s，说明了驾驶员在交叉口变更车道过程中绿信比也是一个较为重要的影响因素，并且信号控制也可以缓解城市的交通拥堵.对于设置信号控制的交叉口来说，设计合理的绿信比，无论驾驶员换道与否，道路通行效率都很高.

2)本文研究还存在一定的缺陷，只是利用MATLAB进行仿真，其参数设置都趋于标准化，而道路条件千变万化，模拟的结果会存在一定的误差，并且将模拟仿真的结果与现实道路相结合也还存在一定的困难，也对后续的深入研究提供了一个更好的思路，为将来智能交通的发展具有一定帮助.