基于宽频信息挖掘的同塔双回输电线路单端故障测距研究

宋 建，束洪春，董 俊，梁雨婷，单节杉，常 勇

(昆明理工大学 电力工程学院，云南 昆明 650500)

0 引 言

同塔双回输电方式因具有线路出线走廊窄、输电容量大、建设周期较短、经济效益好等主要优势，一直在高压输电线路建设中占据着重要作用.由于高压输电往往涉及不同的用电区域，线路一旦发生故障，对整个输电系统运行可靠性影响比单回线路更大，波及范围更广.因此，对同塔双回输电线路的故障测距进行研究仍具有重要的现实意义.

输电线路故障定位多采用故障工频电量检测和故障行波检测两种方法[1-7]，前者多适用于线路相对较短、电压等级较低的输电网络，该方法不考虑等值电源阻抗的变化，相对误差较大；文献[8]采用组合方式进行，利用不同的模量速度进行测距，克服由于模量衰减带来的误差；文献[9-11]提出采用测算故障点弧光放电模型进行测距，给出建立非线性弧光负载模型的方法；文献[12-13]提出利用自然频率与故障距离之间的关系，运用复小波变换寻求该特定频率，并建立该频率与故障距离的函数关系式.上述文献多采用行波法测距，并对行波传输过程进行详细的推理，形成完整行波传输体系.因此，行波法是目前线路故障测距的首选方法，该方法充分运用电磁波的波粒二象性，挖掘电磁波传输特性，利用电磁波的速度进行故障测距，从而绕开电源阻抗变化带来的影响.但是，该方法用于单端线路测距时，第二次反射点的位置与故障位置和故障状态有密切关系，不同的线路结构和运行方式导致识别困难，往往造成测距失败；同时，采用单端法时，近端故障往往存在“死区”.因此，以上问题成为行波法进行单端测距的主要难点，无法形成统一的应用模型.针对上述分析，在同塔双回输电线路场景中，可充分考虑线路的特殊结构，利用非故障线路作信号通道，完成对故障线路的单端测距，从而克服传统单端测距的缺点.

基于同塔双回输电线路的这一特点，提出利用三相瞬时功率的单端故障测距方法进行故障测距.首先，通过同塔双回线路单端两回线上检测到的暂态电气量进行频谱分解，将分解信息利用BP神经网络算法区分故障线路与非故障线路；然后，计算输电线路三相瞬时功率，利用S变换作为暂态信号分析工具[14-16]，寻找故障线路与非故障线路的三相瞬时功率突变的时间点，以此来实现故障线路的单端故障测距.

1 基于BP算法的故障线路鉴别

输电线路发生故障时，根据电路叠加理论，相当于在原来电路上叠加了由于故障产生的高频暂态电路，并在线路中激励出往返振荡的高频响应，从而形成宽频信息量.该信息除了反应原拓扑电路物理量的变化外，还将同步呈现故障电路信息.挖掘信息之间的关系，区分线路状态，不同状态的线路赋予与其相应的数据处理方法，从而实现对故障线路的有效鉴别.

1.1 线路频谱特征分析

对于同塔双回输电线路，如果发生故障时把两回线路同时切除，虽然能保证供电安全，但牺牲了供电可靠性，特别是对特高压输电回路，区域间电气联系应尽最大可能保持，从而避免更大范围的停电事故发生.因此，调度一般在一回线路发生故障时，并行线路仍处于运行状态，从而保证输电连续性，这一现实操作为该测距方案的实施提供了必要条件.

输电线路故障暂态电气量的频宽因故障位置的不同而不同.某点发生故障后，由于耦合的暂态电气量到达检测点的路径不同，从而导致衰减程度存在差异.建立宽频信息的检测，比对宽频信息量之间的关系，确定双回线中的故障线路，该过程可看作是粗略定线.在同塔双回输电线路中，设置如图1所示的信号检测点.进行同端检测时，由于故障暂态量存在衰减，故障线路端检测点与健全线路端检测点监测到的暂态电气量存在较大差别，可根据这一特征区分故障线路和健全线路.

图1 同塔双回输电线路故障暂态量检测点示意图Fig.1 Schematic diagram of fault transient detection point of double-circuit transmission line on the same tower

以一端为例，采用快速傅里叶变换 (FFT)提取故障发生时检测点1和检测点2的宽频信息，对比同塔双回线路的故障与健全两条输电线路，分解两条线路上的宽频信号频谱特征图谱，如图2所示.可以看出，当其中一回线路发生故障时，同塔双回线路中的故障线路与健全线路同侧检测点频谱图有着明显的差异.

当Ⅰ回线路发生故障，Ⅱ回线路为非故障线路时，故障线路与健全线路相比，故障线路检测点检测到大量高频谐波分量，而非故障线路同端检测点中所含高频谐波分量衰减明显.利用合理的算法，构造适当判据，从而区别出故障所在线路.故障线路作为进一步的测距对象，健全线路形成信号导引线，从而形成单端闭环.

1.2 BP算法原理

由于故障距离和图2中的宽频信息之间呈现出复杂的多边非线性关系，故无法用确定的线性函数关系描述，而BP神经网络算法特点之一就是预测过程没有确定的数学函数关系式[17-20].对于多因素影响的输电线路故障距离，且故障距离与宽频信息为非线性关系时，使用BP神经网络进行预测，能够将多边因素综合考虑，且对非线性的映射处理较好，由此拟合的预测模型具有较高精度的区分能力.

图2 同塔双回两回线路中故障与健全线路检测点频谱图Fig.2 Fault in double-circuit and two-circuit transmission lines on the same tower and improvement of the frequency spectrum of line detection points

BP神经网络的基本过程是输入信号的正向传播和误差信号的逆向传播.通过比较逆向传播期望和实际结果之间的误差，不断地调整权值与阀值，直到误差达到可允许的范围，其实质就是沿着权值与阀值的导数负梯度，利用梯度下降法，通过层层迭代降低误差.BP神经网络模型可以分为输入层、隐含层和输出层，其相互关系如图3所示.每一层都含有多个神经单元，各层内的神经单元相互独立，而相邻层之间的神经单元相互连接，每一层的神经单元只能受上一层神经单元的作用.

图3 BP神经网络结构图Fig.3 BP neural network structure

采用BP神经网络建模时，要确定网络的各层层数、层内的神经单元数、输入量和输出量的个数，初始化输入层和隐藏层之间的权值、隐藏层和输出层之间的权值、各层的阈值，设置学习过程的学习效率和迭代次数.取一对输入数据开始网络训练，最后确定各层输入输出计算的结果.

设输入为Pj，输出为Qj，隐藏层的输入输出方程如式(1)所示：

(1)

式中：Wij为输入层与隐藏层之间的权值，θj为隐藏层的阈值，aj为输入信号变量，f为激活函数.

设输出层的输入为Ut，输出为Vt，其对应的方程如式(2)所示：

(2)

式中，θt为输出层的阈值.

输入层首先接受样本的信息输入信号，层内神经单元由获得的信息生成相应的权值输送给隐藏层，再由隐藏层生成相应的连接权值给输出层传递信号，最后输出层输出结果.隐含层与输出层略有不同，计算权值Wij对误差的影响时，需将各输出单元对Qj的误差进行累加.当累加数值满足跳转要求时，才转入下一对输入数据的训练，形成如图4所示数据处理流程.

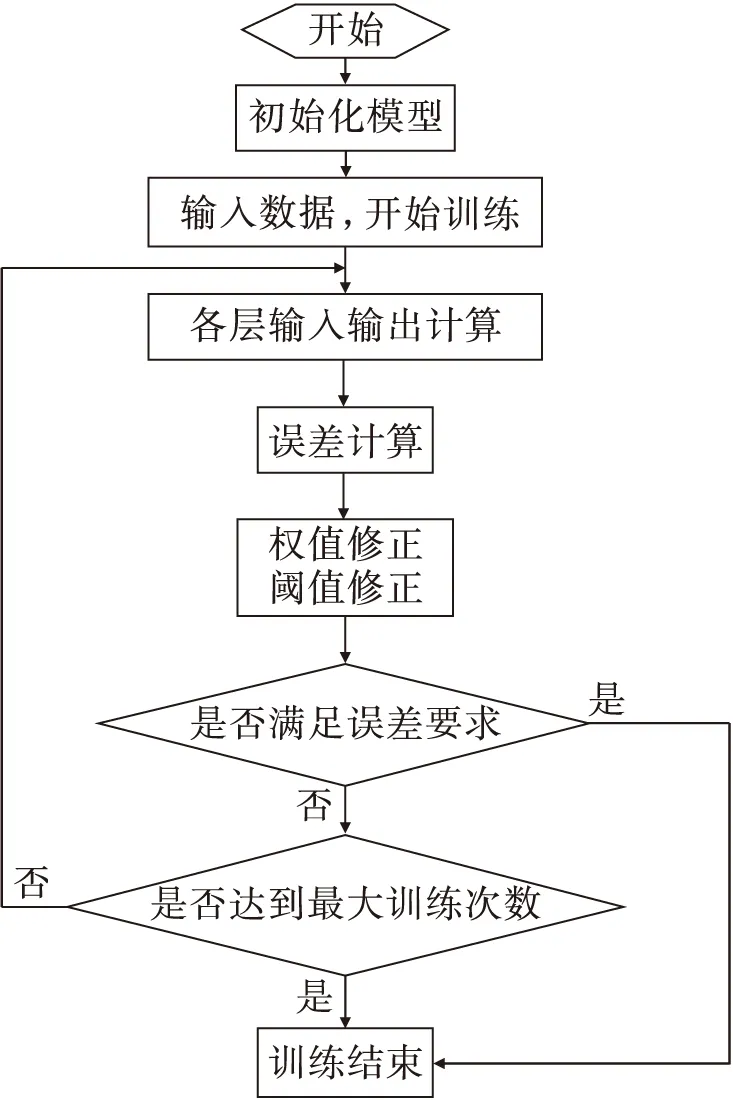
图4 BP神经网络数据处理算法流程Fig.4 Data processing algorithm flow of BP neural network

通过BP网络的这种不断反复地训练，无需具体的输入输出之间的映射关系，就可以获得具有较强自适应能力和容错能力的网络模型.

1.3 BP神经网络算法判别线路

将线路高频宽带信号的特征进行有效放大，以此作为故障特征量进行故障线路和非故障线路的区分，线路的鉴别算法涉及到大量非线性方程求解，适合采用智能算法.BP神经网络经过充分训练后可以逼近目标期望的数学模型，具有较强的自适应性和自主学习能力，可以通过神经网络对输入的向量进行分析和推理，从而实现计算、记忆、联想、识别这些功能.所以，选择通过神经网络算法对输电线路故障与否进行判别，综合运用线路零序电流频谱信息与BP神经网络对同塔双回输电线路状态进行判别.

根据线路CT的实际位置，以同塔双回线路保护端采集到的故障零序电流经过FFT变换得出的频谱为目标，提取频谱数据中的频段与对应的幅值信息输入，得出其对应的线路状态.输出量为0或1(0为健全线路，1为故障线路)时，需要实现的函数映射关系如式(3)所示(其中，输入量为电流量和变换后的宽频信号的频带)：

(3)

在实现选线之前，需建立同塔双回输电线路模型，对其中的一回线路设置接地故障，并对不同故障状态进行仿真，得到BP神经网络所需的训练样本.分别对故障发生后的所有回线所对应的零序电流信号进行FFT变换，得到各自对应的频谱图.提取频谱图上的频率与其对应的幅值作为训练样本输入BP神经网络中，双回线路的各自状态作为输出，实现线路零序电流与目标回线状态(健全或故障)的非线性映射，从而实现定线目标，其流程如图5所示.

图5 故障线路鉴别流程图Fig.5 Flow chart of fault line identification

2 单端测距方程

当同塔双回高压输电线路的其中某回线路发生故障，故障点将产生故障行波，并由故障点向两侧传递.故障行波信号是一种高频暂态信号，同塔双回线路各相间耦合复杂，用传统的相模变换得到的模电流分量或模电压分量传播特性存在较大的差异，对行波波头的选取较为困难.BP神经网络鉴别出故障回线后，提取同端检测对应暂态电气量，利用公式(4)计算输电线路三相瞬时功率.利用式(5)S变换作为暂态信号分析工具，寻找故障线路与非故障线路的三相瞬时功率突变的时间点，以此来实现故障测距.测距过程充分挖掘故障后的高频信息进行故障线路测距，无需考虑两端时钟同步的难题.考虑线路之间存在耦合关系，运用凯伦贝尔矩阵对测点采集到的三相信号进行解耦：

P(t)=Δua×Δia+Δub×Δib+Δuc×Δic

(4)

(5)

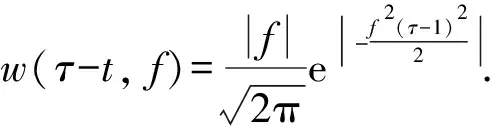
图6为同塔双回线路I回线路某一点发生故障时的故障行波网格图，设故障长度为L，列写故障发生后的传输方程如式(6)所示：

图6 同塔双回线路故障时的故障行波网格图Fig.6 Fault traveling wave grid diagram of the double loop line in the same tower

(6)

式中：x为故障距离，v为对应频率的波速度，t为故障发生时间，t1、t2为故障初始行波到达故障线路M端测量点和非故障线路N端测量点的时间.化简后得最终单端测距方程，如式7所示：

(7)

3 仿真实例

3.1故障线路的鉴别

以单相接地故障为例，进行同塔双回输电线路的故障模拟.采用电力系统电磁暂态仿真软件PSCAD/EMTDC对输电线路进行仿真建模与故障模拟，以Matlab进行编程验证.以平武线路为模拟对象，在原有单回线路基础上建立双回仿真模型，如图7所示.输电线路全长为L=600 km,模拟系统阻抗参数如图5所示.

图7 同杆双回输电线路仿真系统图Fig.7 Same-sole double-circuit transmission line simulation system diagram

设置不同的故障位置来获取BP神经网络算法的训练样本，对其中一回线路，在不同位置 (位于线路长度的5%,10%,15%,…,90%,95%)进行故障设置，得到的故障数据样本经FFT处理后输入到BP神经网络中，样本数量为500个，利用Matlab对BP神经网络进行训练，训练测试结果如表1所示.

表1 选线样本测试结果

3.2 单端故障测距验证

宽频故障信息经过时—频变换后，作为BP神经网络的输入进行线路区分，鉴别出故障线路和非故障线路.设故障发生时刻为0.305 s，故障类型为Ⅰ回发生A相接地故障，采样频率设置为1MHz.以M端为例，对其检测点1和检测点2进行故障电流检测，以此为测试数据，进行故障线路的测距.利用公式(7)对宽频信息进行三相瞬时功率计算，形成图8所示的瞬时性功率谱，进一步将瞬时性功率做S变换，以寻求行波的突变时刻，可以表现为幅值的突变.经S变换后得到如图9所示的模矩阵，综合观察S模矩阵多个频率点下幅值—时间曲线，寻找故障对应主频率突变时刻，标定公式(7)中的突变时间.

图8 同塔双回线路发生故障时两回线的三相瞬时功率图Fig.8 Three-phase instantaneous power diagram of two circuits in case of fault of double circuit in the same tower

图9 两回线的三相瞬时功率经S变换得出的幅值—频率—时间图Fig.9 Amplitude-frequency-time diagram obtained by S transformation of the three-phase instantaneous power of two loops

同塔双回线路Ⅰ回线发生故障时，非故障线路的三相瞬时功率曲线，以及对其做了S变换之后50 Hz、200 Hz、400 Hz的幅值—时间曲线，如图10所示.比较后选择400 Hz的幅值曲线图进行幅值突变点的定位，找出极大值点，并标定出幅值突变的时间点.

图10 非故障回线的三相瞬时功率曲线与对应的幅值—时间图Fig.10 Three-phase instantaneous power curve of the non-fault loop and the corresponding amplitude-time diagram

将三相瞬时功率经S变换后得到模矩阵，选择400 Hz的幅值曲线图进行幅值突变点的定位，找出极大值点，并标定出幅值突变的时间点，其中一组如图11所示.标定突变点时间后，运用式(7)进行故障距离计算.改变不同故障位置，验证方法的有效性，测试结果如表2所示.

图11 S变换后的突变时间标定Fig.11 Calibration of mutation time after S transformation

表2 不同情况的测距结果

根据表2测距结果，该单端测距测距误差均在0 ～0.5 km之间，结果准确可靠.

4 结论

通过对同塔双回输电线路单端故障暂态信息进行分析，运用宽频暂态信息衰减与流通路径之间的关系，建立了同塔双回输电线路单端测距模型.采用BP神经网络算法对非线性测距模型中的线路进行鉴别，区分出双回线中的故障线路和健全线路.将故障线路作为测距目标，健全线路作为宽频信号的环形导引线，求解出其三相瞬时性功率，运用S变换进行瞬时性突变点选择，构造由故障线路和健全线路串联结构下的单端测距方程.该测距方程避免了传统单端测距中无法可靠判别第二次反射位置的困扰，同时，当线路发生近端故障时，传统单端测距方程存在故障测距的“死区”问题，采用双回线的串联结构测距方程有效避免了该问题，并通过仿真验证了该测距方法的有效性.