高温气冷球床堆有效导热系数模型的改进
陈 波,步珊珊,陈德奇,马在勇,张卢腾
(重庆大学 低品位能源利用技术及系统教育部重点实验室,重庆 400044)
高温气冷堆是国际领先的第4代核能技术,具有经济性和固有安全性等特点[1]。高温气冷球床堆采用球形全陶瓷包覆颗粒作为燃料元件,其安全设计准则要求:在任何事故情况下,球床堆芯的衰变余热依靠辐射换热和导热等非能动传热机制导出,实现事故停堆后的冷却,以保证燃料包壳不发生破裂,将放射性物质限制在内[2]。高温气冷球床堆堆芯内的热量传递机制十分复杂,通常将球床内的导热、辐射换热等复杂传热机制等效为简单的热传导过程,采用一个综合的有效导热系数来表征。因此有效导热系数是表征球床堆芯宏观传热能力的关键参数[3],也是高温气冷球床堆热工设计与安全分析程序中的基本参数。
事故工况下,当冷却剂失去强制流动后,对流传热不考虑,高温气冷球床堆堆芯的有效导热系数主要由3部分组成[4]:1) 固体表面间的辐射换热;2) 球体颗粒的导热和流体的导热,即气-固导热;3) 相邻颗粒接触点之间的接触导热。Zehner等[5]基于圆柱单元方法提出了计算球床有效导热系数的ZS模型,这一模型可很好地计算球床的气-固导热[6],但未考虑接触导热和辐射换热。Bauer等[7]采用了接触面积系数φ来考虑接触导热,同时使用Breitbach等[8]模型来计算辐射换热,这一改进后的模型被称为ZBS模型。ZBS模型被广泛应用于预测球床有效导热系数的计算。当温度低于1 000 ℃ 时,Wu等[9]发现ZBS模型可很好地预测德国SANA实验和南非HTTU实验的测量结果。de Beer等[10]发现在球床主体区域,ZBS模型预测值略低于实验值。Bu等[11]的实验结果也表明ZBS模型对球床有效导热系数的预测性能要优于其他模型。然而,ZBS模型预测值对接触面积系数φ十分敏感[12],一般通过实验值来调整φ的取值,如Antwerpen等[13]发现当φ=0.01时,ZBS模型与实验结果吻合较好。Bu等[12]发现,当φ=0.07时ZBS模型预测值和简单立方球床的实验测量结果的平均相对误差小于5%。目前关于接触面积系数φ的计算表达式较少,只有Chen等[14]和You等[15]分别给出了φ的计算表达式。
在前期工作的基础上[6,11-12,16],本文数值模拟不同球床结构的有效导热系数,通过多元线性回归获得接触面积系数φ的计算表达式。通过与SANA实验结果及前期实验结果的对比,评估改进后的ZBS模型的预测能力。
1 物理模型和数值方法
1.1 ZBS模型
Bauer等[7]基于圆柱单位元提出并联的3条传热路径,并采用分布系数加权叠加接触导热、气固导热和辐射换热来预测球床结构的有效导热系数,这种理论模型被称为ZBS模型,由于该模型具有良好的预测性而被广泛关注。ZBS模型如下:
(1)
其中:keff为有效导热系数,W/(m·K);kf为流体导热系数,W/(m·K);ε为孔隙率;κ为气-固导热系数比;κr为辐射换热系数比;κG为Knudsen状态下的气体导热系数比,这里取1;κc为综合导热系数比,计算方法见文献[4];φ为接触面积系数,是一个表征接触导热份额的无量纲系数,可表示为:
φ=aNcm·γn
(2)
其中:Nc为配位数;γ为接触直径比,γ=dc/dp,dc和dp分别为接触直径和球径。系数a和指数m、n通过多元线性回归方法求解,因此需要获得不同配位数Nc及接触直径比γ对应的接触面积系数φ的值。
1.2 数值计算模型
为获得多元线性回归需要的数据,本文针对不同几何参数的球床有效导热系数进行数值分析。如图1所示,采用简单立方(SC)、体心立方(BCC)、面心立方(FCC)和无序4种堆积结构单元,这4种结构的配位数Nc分别为6、8、12和5.5。无序堆积结构单元的生成方法为:基于PFC3D软件和膨胀法生成直径为15dp、高度为15dp的大球床,然后从大球床的中心区域中抽取出来2.5dp×2.4dp×2.6dp的结构单元。每种堆积结构单元分别构建了0.035、0.050和0.100 3种不同的接触直径比γ,因此有12组不同配位数Nc及接触直径比γ对应的球床结构模型(表1)。

结构单元:a——SC;b——BCC;c——FCC;d——无序

表1 不同几何模型的参数
1.3 数值方法
本文计算中流体无流动,球床内无内热源,只需求解固体区域和流体区域的能量方程。流体和固体区域的能量方程为:
(3)
其中:ki为固体(石墨)和流体(氮气/氦气)的导热系数,W/(m·K),并随温度变化;i=s、f,分别代表固相和气相;T为温度;x、y、z表示空间坐标。
获得球床温度分布后,通过逆求解一维傅里叶导热定律获得有效导热系数:
(4)
其中:q为平均热流密度,W/m2;ΔT为高温壁面和低温壁面的温差,10 K;Δz为高温壁面和低温壁面的距离,m。
模型1的计算区域和边界条件如图2所示。z方向前后的高温壁面和低温壁面是定温边界条件;堆积单元的平均温度范围为373~1 073 K;垂直于xy平面的另外4个表面是绝热的,固体颗粒和氮气/氦气的交界面无滑移。将以上模型导入ANSYS Fluent 15.0中计算,求解器基于压力求解,求解算法选用SIMPLE算法,离散格式采用二阶迎风格式,采用残差小于10-12作为收敛判据。本文数值计算模型的验证详见文献[6]。
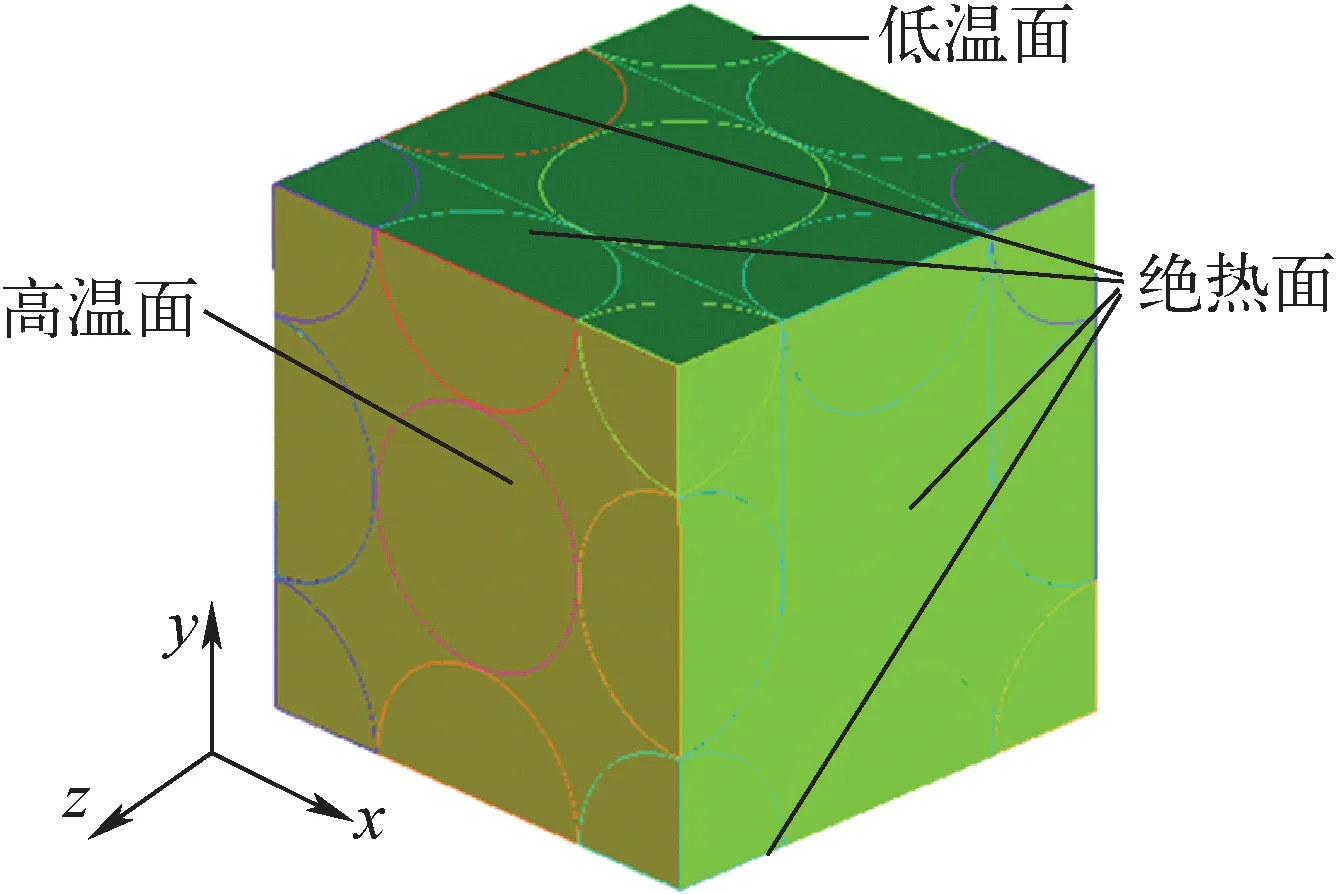
图2 模型1计算区域和边界条件
1.4 网格独立性验证
采用ICEM软件对几何模型划分了3套非结构化网格,对模型1进行网格无关性考核,结果列于表2。和第3套网格的计算结果相比,第1和第2套网格计算得到的有效导热系数相对偏差分别为1.43%和0.29%,因此可认为第2套网格获得网格无关解。以无序球床结构单元为例,模型10网格划分示意图如图3所示,接触区域和颗粒表面均进行了适当的加密。

表2 模型1网格独立性验证
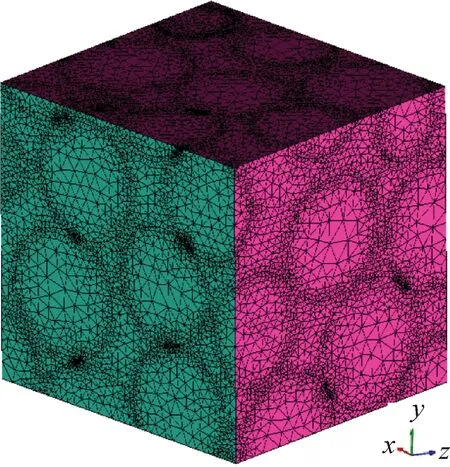
图3 模型10网格划分示意图
2 接触面积系数的多元线性回归
通过调整接触面积系数φ的值,使得ZBS模型的预测值与数值计算结果的平均相对误差最小,来获得不同配位数Nc及接触直径比γ对应的接触面积系数φ的值。以模型1为例,如图4所示,ZBS模型预测值对φ十分敏感。随着φ的取值减小,ZBS的预测值也减小。如图5所示,不同φ对应的预测值和数值计算结果的平均相对误差先减小后增大。平均相对误差的绝对值最小时对应的φ就是ZBS模型中φ的最优取值,因此可获得模型1对应的φ为0.105。通过同样的分析方法获得了12组不同配位数Nc及接触直径比γ对应的φ,结果列于表3。
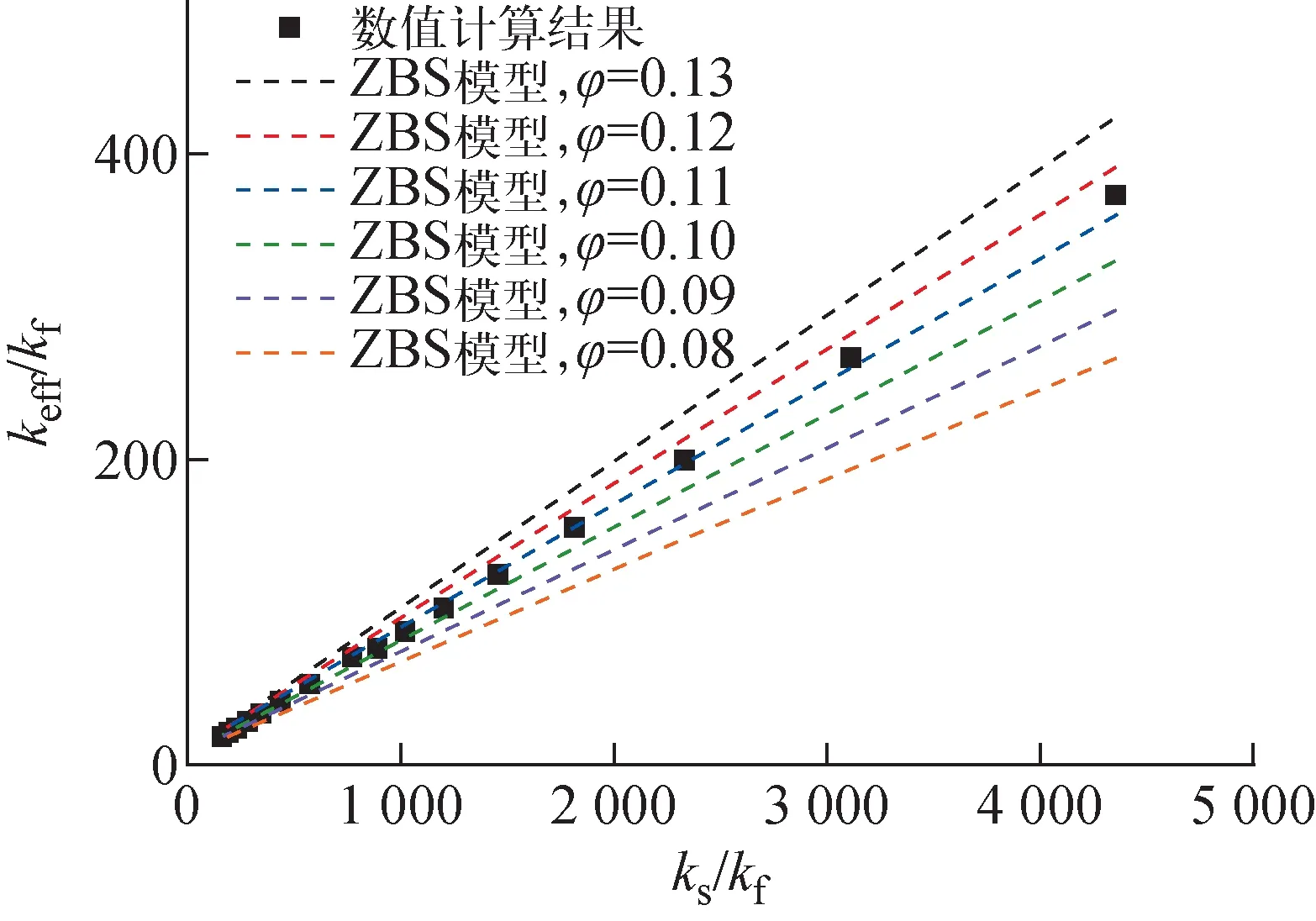
图4 模型1模拟结果与ZBS模型预测值的对比
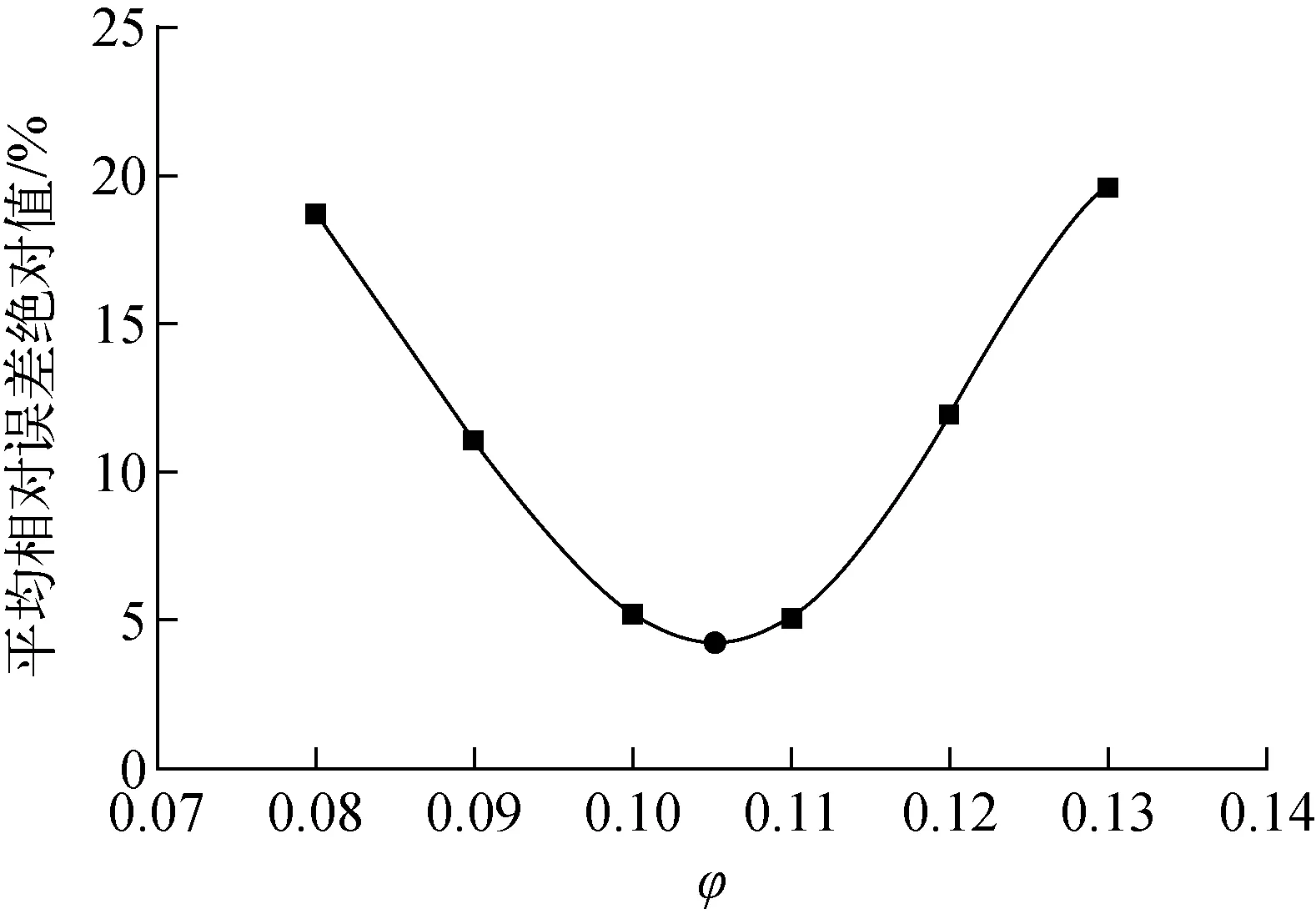
图5 相对误差的绝对值分布

表3 不同配位数Nc和接触直径比γ对应下的φ
为进行多元线性回归,式(1)变换为下面的形式:
lnφ=lna+mlnNc+nlnγ
(5)
然后采用最小二乘法对表3中的数据进行拟合,获得φ的表达式为:
φ=0.21Ncγ
(6)
对于真实的无序球床结构,Nc可通过以下表达式[17]计算:
Nc=25.952ε3-62.364ε2+
39.724ε-2.023 3 0.26≤ε≤0.48
(7)
接触直径比γ=dc/dp,dc可根据下式[18]计算:
(8)
其中:μp为泊松比;Ep为杨氏弹性模量,Pa;F为外加作用力,N;rp为球的半径。因此接触直径比γ也可求解。确定了球床结构的Nc及γ,ZBS模型中的φ可根据式(6)求解获得。式(6)适用于孔隙率为0.260~0.48、温度范围为273~1 100 K的球床结构。
3 改进后的ZBS模型预测能力评估
采用SANA实验结果[19]评估改进后的ZBS模型预测能力。SANA实验装置针对氮气/氦气氛围下的球床等效导热系数进行了测量,石墨球床的颗粒直径dp为60 mm,圆筒堆积球床直径为25dp,高度为1 m,孔隙率为0.39,测试温度范围为273~1 223 K。改进后的ZBS模型和SANA实验结果对比如图6所示。由图6可见,改进后的ZBS模型预测能力在中低温工况下(小于1 000 K)要优于其他模型(包括IAEA ZS模型[19]、MSUC模型[13]、Chen模型[14]和You模型[15])。在高温工况下(大于1 000 K),改进后的ZBS模型预测能力和IAEA ZS模型[19]和MSUC模型[13]相当。当温度大于1 000 K左右,球床主导的传热机制从接触导热转变为辐射传热机制[20]。Chen模型和You模型均是基于ZBS模型的改进,其中Chen模型可预测两种不同直径颗粒堆积成的二元球床的有效导热系数,You模型改进了ZBS模型中的辐射传热模型。由于Chen模型和You模型中提出的接触面积系数φ预测值(分别为0.019和0.003)要比本文的计算值(0.033)小很多,低估了接触导热,因此在中低温工况下对球床有效导热系数的预测值偏小。IAEA ZS模型中将气-固导热、接触导热和辐射传热机制对应的传热系数直接叠加,其中接触导热部分采用Chen-Tien模型[21]计算。MSUC模型中接触导热系数的计算方法与IAEA ZS模型相同。综合以上分析,改进后的ZBS模型对于接触导热的贡献有较好地预测能力,这说明本文提出的φ的计算表达式有较高的可靠性。值得注意的是,目前所有模型的预测值均比SANA实验结果小。原因可能是SANA实验中自然对流效应比较显著,而以上所有模型都未考虑自然对流的影响。

图6 改进后的ZBS模型与SANA实验结果对比
本课题组前期开展了球床有效导热系数实验测量[11,16],实验系统主要包括长方体球床堆芯、氮气供应系统、加热电源与控制系统、冷却水系统和温度数据采集系统5部分。如图7所示,直流电加热板与石墨球床的高温壁面接触,球床的4个侧壁面均包裹保温层,尽量减少堆芯散热,使热量主要向另外一侧的低温壁面传递,然后被低温壁面侧的冷却水带走热量。在实验测量中,压力控制在40 kPa,自然对流效应被大大抑制。石墨球床的颗粒直径dp为15 mm,长方体堆积球床为6dp×6dp×14dp,孔隙率为0.40,实验中高温壁面温度范围为380~800 K。如图8所示,在球床主体区域(距壁面大于4个颗粒直径),改进后的ZBS模型和实验结果吻合得很好,最大相对误差只有12.6%。但在近壁面区域(距壁面4个颗粒直径以内)和实验值误差较大,这说明改进后的ZBS模型在球床近壁面区域的预测能力较差。由于壁面限制,球床在近壁面区域的几何结构与主体区域有显著不同,如孔隙率在近壁面区域大同时波动强烈(壁面效应),因此近壁面区域有效导热系数会明显小于主体区域的有效导热系数,但ZBS模型(包括基于ZBS模型的改进模型)的推导未考虑到这种壁面效应,因此ZBS模型在球床近壁面区域的预测能力较差。
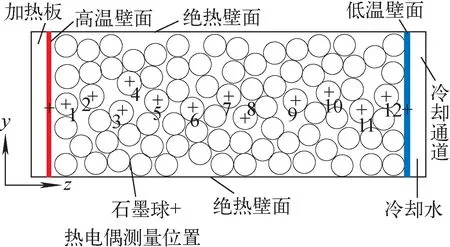
图7 实验中球床示意图
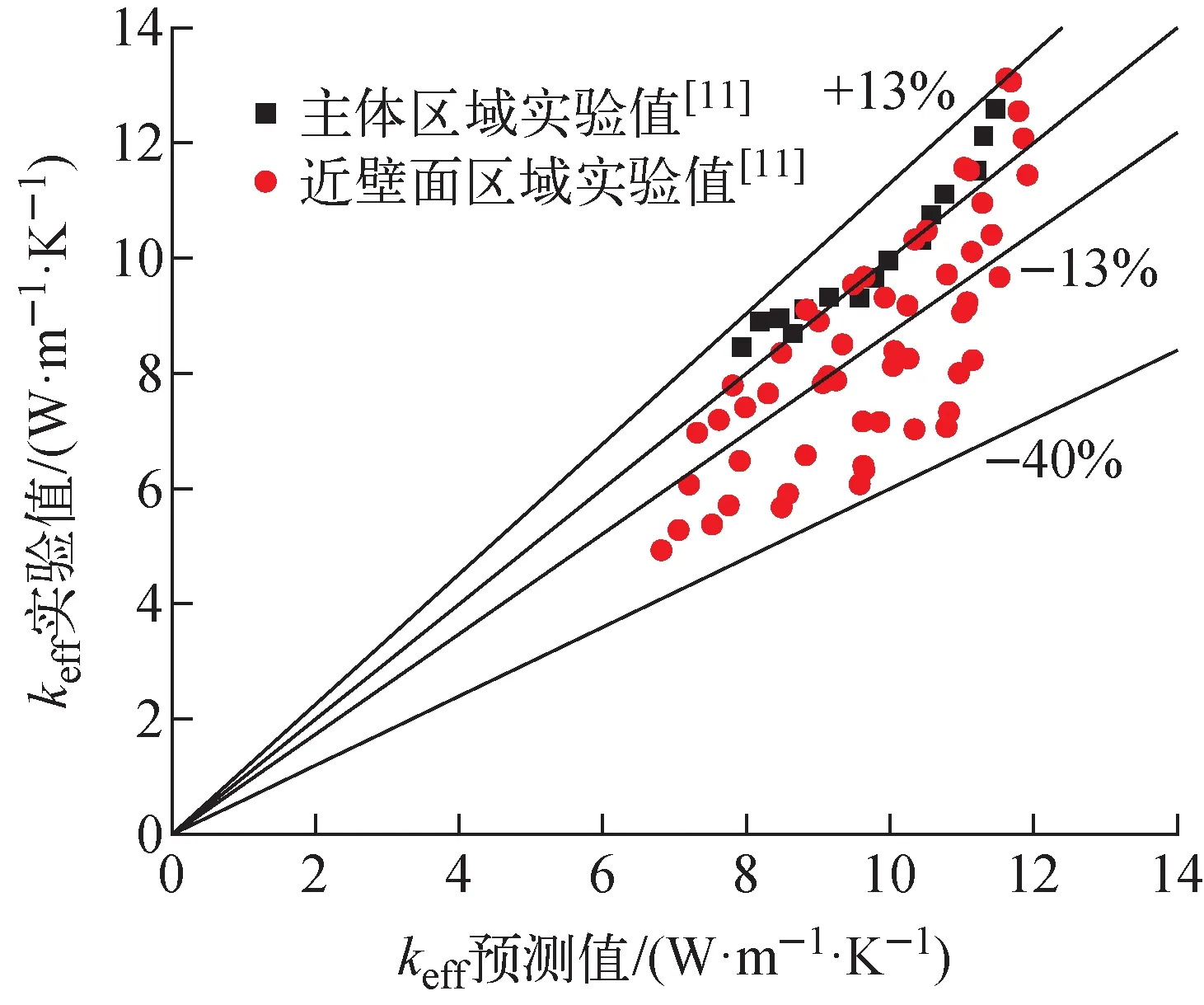
图8 改进后的ZBS模型和前期实验结果对比
4 结论
为提高ZBS模型对球床结构有效导热系数的预测能力,本文数值模拟了不同结构球床的有效导热系数,通过多元线性回归获得了ZBS模型中经验参数接触面积系数φ的计算表达式。与SANA实验结果对比表明,改进后的ZBS模型的预测能力优于其他球床有效导热系数模型。和前期的实验结果对比,改进后的ZBS模型的计算结果在球床主体区域吻合很好,但在近壁面区域吻合较差。因此,改进后的ZBS模型可用于孔隙率为0.26~0.48、温度在273~1 100 K之间的球床结构主体区域有效导热系数预测。

