5×5花瓣形燃料棒束组件内单相流动与换热特性数值模拟研究
蔡伟华,韦徵圣,李石磊,张文超,*,侯延栋,*
(1.东北电力大学 热流科学与核工程实验室,吉林 吉林 132012;2.中广核研究院有限公司,广东 深圳 518031)
核能是安全、低碳、高功率密度的清洁能源。为了提高核能的经济性,适应越来越高的核安全标准,提高压水堆设计功率密度是优化反应堆设计的重要途径,通过改进燃料棒几何结构设计高性能燃料棒成为反应堆领域的一个主要研究方向。近年来提出了一些新型燃料元件,如绕丝型燃料元件、环形燃料元件和球形燃料元件等,国内外学者对新型燃料元件开展了大量的研究,其中,一种截面为花瓣形的新型燃料元件因其优异的热工水力性能而受到学者关注。花瓣形燃料元件最早由苏联提出,相较于传统圆棒形燃料元件,花瓣形燃料元件具有以下优点[1]:1) 具有较大的表面积-体积比,可增加冷却面积、降低平均热流;2) 螺旋结构可增强通道内冷却剂的交混程度;3) 自支撑结构可降低通道间阻力,简化堆芯结构。目前,针对花瓣形燃料棒束组件内流动与换热特性,国内外学者已展开了相关研究。Nikolai等[2]分析讨论了氦冷快堆中花瓣形燃料棒的应用。Ageenkov等[3]研究了花瓣形燃料棒在高通量束流反应堆PIK和SM-3中的应用,确定了基本几何参数和质量参数。Diakov等[4]开发了基于俄罗斯核动力破冰船KLT-40核反应堆堆芯的计算模型,模拟了具有花瓣形燃料棒的堆芯中子学行为,分析其在核破冰船中的应用。Bol′shakov等[5]对7根花瓣形燃料棒组件进行了实验研究,发现与传统燃料组件相比,通道压降基本相等,表面临界热流密度更高。美国麻省理工学院(MIT)和美国光桥公司(Lightbridge)对花瓣形燃料组件进行了实验和数值模拟研究[6-8],探究了花瓣形燃料组件提升压水堆和沸水堆功率密度的可行性。Shirvan等[9]针对4×4花瓣形燃料组件开展了数值研究,并与麻省理工学院的实验结果进行对比分析,发现在压水堆和沸水堆条件下的总压降比实验经验关系式计算值高10%左右。Shirvan[10]的研究表明,将花瓣形燃料棒替换至现役压水堆中,最大功率提升可达25%。张琦等[11]采用空气作为冷却剂开展了5×5花瓣形燃料组件内流动与换热特性数值研究,研究结果表明,在低速范围内燃料螺旋节距对流动阻力影响较小,在整个流速范围内对换热效果影响显著。邹旭毛等[12]采用水作为冷却剂对花瓣形燃料组件内的流动换热特性进行了数值模拟,探究了三维流场与温度场分布特性,分析了燃料棒螺旋节距和主流速度对流动与换热的影响。张琦等[13]开展了5×5花瓣形燃料组件内热工水力实验,测量了组件内的沿程压降和各子通道内的水温分布,获得了该组件的摩擦系数经验关系式和交混系数。
从上述研究可知,花瓣形燃料组件流动与换热性能优于传统格架式棒束组件,但国内外相关研究对于花瓣形燃料组件棒束通道内流动与换热特性的机理认识还不深,相关研究也较少。近年来利用CFD方法对高保真燃料组件进行模拟,获取组件内详细三维流动与传热特性,进而针对组件结构进行设计优化成为核工程研究的一个重要手段[14-16]。因此,本文通过数值模拟方法,对5×5花瓣形燃料组件进行研究,分析组件内的三维流动与换热特性。
1 计算模型
1.1 几何模型
本文研究的燃料组件由截面为正方形的外套管与其中呈矩形排列的25根花瓣形燃料棒组成,如图1所示。其中,花瓣形燃料棒外切圆直径为D,内凹弧面半径为R,外凸弧面半径为R/2,外切圆直径与内凹弧面半径之比D/R=5.147,连接外凸弧面与内凹弧面的伸展部分长度之比D/h为8.974,组件外套矩形管边长为L,L/D=5.357,燃料棒螺旋节距为H。
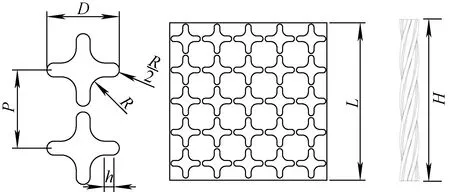
图1 花瓣形燃料组件几何结构
由于实际情况中燃料棒束由各燃料棒间外凸弧面的点接触形成自支撑结构,实际网格划分中存在一定困难,故更改原有紧密排列方式,增加相邻燃料棒的间距以消除点接触,使网格可以更好地嵌入相邻燃料棒间。为探究棒间距对组件流场的影响,选取0.5d、d、1.5d(d=0.5 mm)3种棒间距,建立对应的组件模型并使用相同的边界条件、湍流模型进行计算,组件轴向中心处温度场如图2所示。由图2可看出:不同棒间距组件的中心燃料棒周围温度场分布一致,内凹弧处温度高于外凸弧处温度;对于冷却剂流场,以间距d为基准,各子通道平均温度相对误差分别为σ0.5d=0.07%、σ1.5d=0.14%。综合考虑网格划分等因素后,选取间距d作为后续几何模型的基准,增加间距后相邻燃料棒中心距离为P,P=D+d。
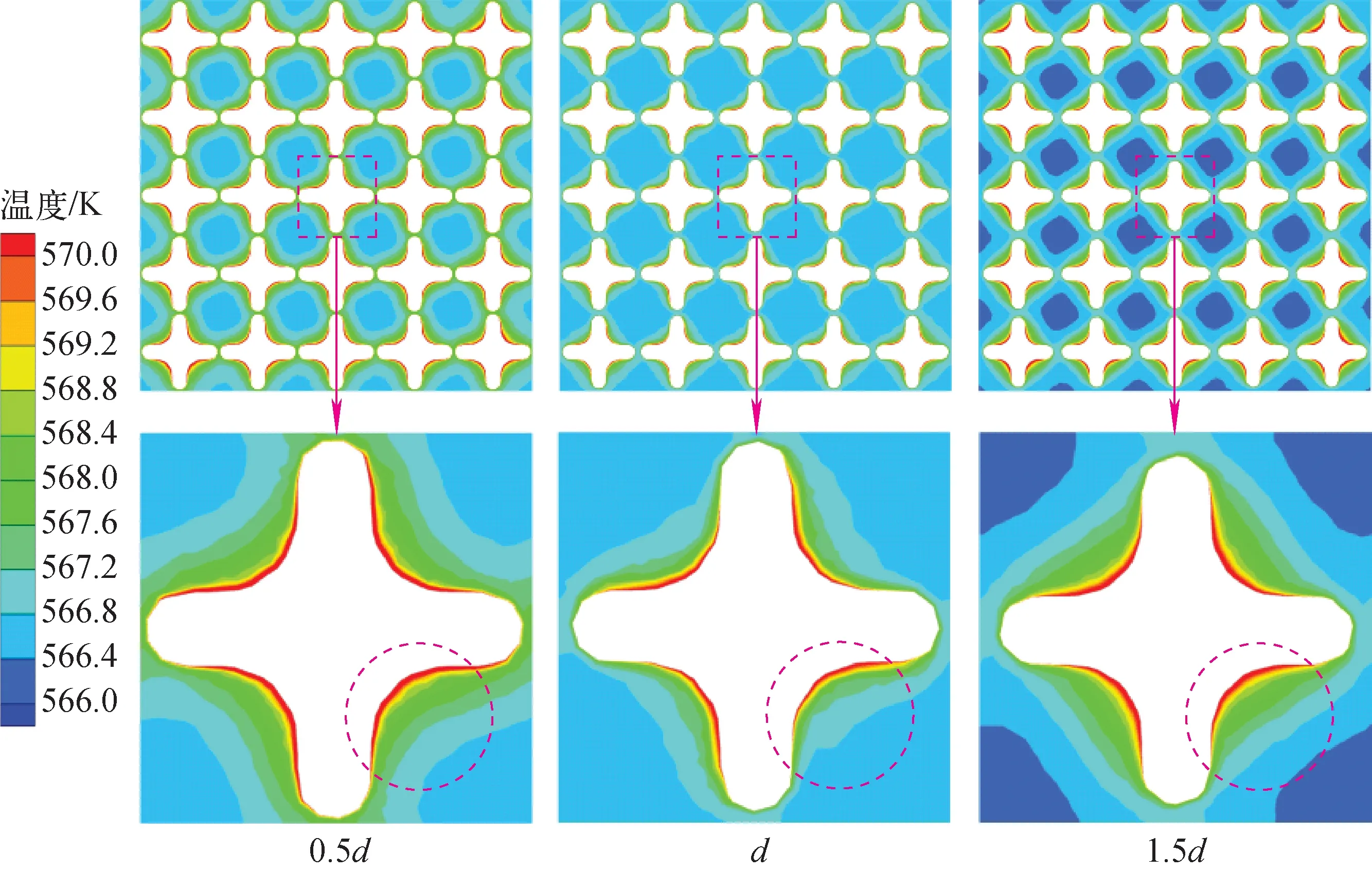
图2 燃料棒间距对组件温度场的影响
1.2 数值模型
1.2.1导热模型 对于固体域,采用稳态计算,导热方程可用下式表示:
(1)
(2)
式中:Qv为体积热源;λs为固体热导率;Ts为固体温度。
1.2.2流固共轭传热模型 流体与固体之间的传热主要通过流固交界面进行传递,在交界面处流体和固体的热流密度、温度具有连续性。
ql|interface=qs|interface
(3)
Tl|interface=Ts|interface
(4)
式中:ql|interface和qs|interface为交界面上流体域和固体域的热流密度;Tl|interface和Ts|interface为交界面上流体和固体的温度。
1.2.3湍流模型验证 本文根据MIT单相压降实验[7]中的花瓣形燃料棒实验件,建立尺寸一致的几何模型,在此基础上分别对Realizablek-ε模型、Standardk-ω模型和SSTk-ω模型进行敏感性分析,将阻力系数f计算结果与实验结果进行对比,如图3所示。由图3可看出,在选取雷诺数范围内,SSTk-ω模型与实验结果的相对误差均在5%以内,最大、最小相对误差分别为4.6%和0.41%;Realizablek-ε模型和Standardk-ω模型的最大相对误差分别为21.7%和16.1%,最小相对误差分别为4.1%和3.3%。因此,选取SSTk-ω模型作为后续的湍流模型进行计算。

图3 花瓣形燃料组件阻力系数变化
1.3 网格划分
本研究使用STAR-CCM+中的多面体网格对组件进行网格划分。燃料棒采用二维网格沿轴向旋转拉伸方式生成网格,可有效减少网格数量。燃料棒与通道交界面处设置边界层,首层网格高度为0.001 mm,近壁面区共设置10层网格。
图4示出5×5花瓣形燃料组件的网格划分,网格质量均在0.5以上。通过调整网格最大、最小尺寸及网格增长率,划分出5套不同数量的网格以完成网格无关性验证,如图5所示。随着网格数目的增加,进出口温差及压差增加,当网格数量达到3 700万之后,温差和压差随着网格数量的增加趋于平缓,故选用网格数量为3 700万的网格进行数值分析。

图4 5×5花瓣形燃料组件网格划分及网格细节

图5 网格无关性验证
1.4 边界条件
针对组件流道、燃料棒建立不同的计算域,参考AP1000压水堆的实际运行参数,组件系统压力为15.5 MPa,组件流道内冷却剂设置为去离子水,物性参数根据IAPWS-IF97关系式确定,密度、定压比热容、导热系数、动力黏度等均随温度变化而变化。燃料棒材质根据光桥公司推荐的铀-锆合金(U-Zr合金)进行设置,物性参数根据Fedorov等[17]给出的实验数据进行关联式拟合并导入STAR-CCM+中。燃料棒区域和组件通道区域交界面使用interface连接进行耦合求解,组件外壁面设置为绝热、无滑移壁面。入口设置为速度入口,入口温度为565.55 K;出口设置为压力出口。光桥公司发表的文献[8]中称,将花瓣形燃料棒替换至现役压水堆中,可提升17%的功率输出,故将花瓣形燃料棒体积释热率设置为AP1000压水堆燃料棒体积释热率的1.17倍,发热方式为均匀加热。表1列出模型结构参数及数值模拟边界条件。

表1 模型结构参数及数值模拟边界条件
2 数值模拟结果与分析
根据流道结构可将冷却剂流动区域分为中心子通道、边子通道和角子通道。为便于模型对比及参数分析,分别沿燃料组件轴向和径向选取7个截面,沿各子通道中心处取1条直线,截面和点的位置如图6所示。图6中,z为轴向距离。
2.1 速度场分析
图7示出表1中工况5轴向不同高度截面(图6中Plane4~Plane7)上径向速度分布云图。由图7可看出:燃料棒表面附近存在较强的二次流动,二次流速度最大值位置出现在Plane6的燃料棒表面内凹弧处附近,最大值为0.1 m/s;在燃料棒两个相邻外凸弧间的区域内(图7中标记为1处)二次流速度较低,平均值为0.03 m/s。在相邻4根燃料棒所围成的子通道的中心区域内(图7中标记为2处),二次流速度最低,平均值为0.01 m/s,这主要是因为该区域距离燃料棒相对较远,受燃料棒螺旋的影响也就相对较小。随着流体的流动,单个燃料棒表面附近流体的二次流速度变化并不明显,但是由于燃料棒的扭转,相邻燃料棒表面之间的距离(下称棒间隙)逐渐增大,相邻子通道之间的交混作用在螺旋结构的影响下逐渐增强。定义不同高度处燃料棒截面形状与入口处燃料棒截面形状之间的旋转角度为相对角度,图7中Plane4对应相对角度为0°时,棒间隙最小,Plane7对应相对角度为45°时,棒间隙最大。在整个棒束长度内,随着燃料棒的扭转,棒间隙呈周期性变化。由相对角度0°增加到45°的过程,是棒间隙增大的过程。之后,相对角度由45°增加到90°的过程,是棒间隙减小的过程,如此每90°形成1个变化周期。受棒间隙周期性变化的影响,相邻子通道之间交混作用的强度也会呈周期性变化。

图6 截面和点位置示意图
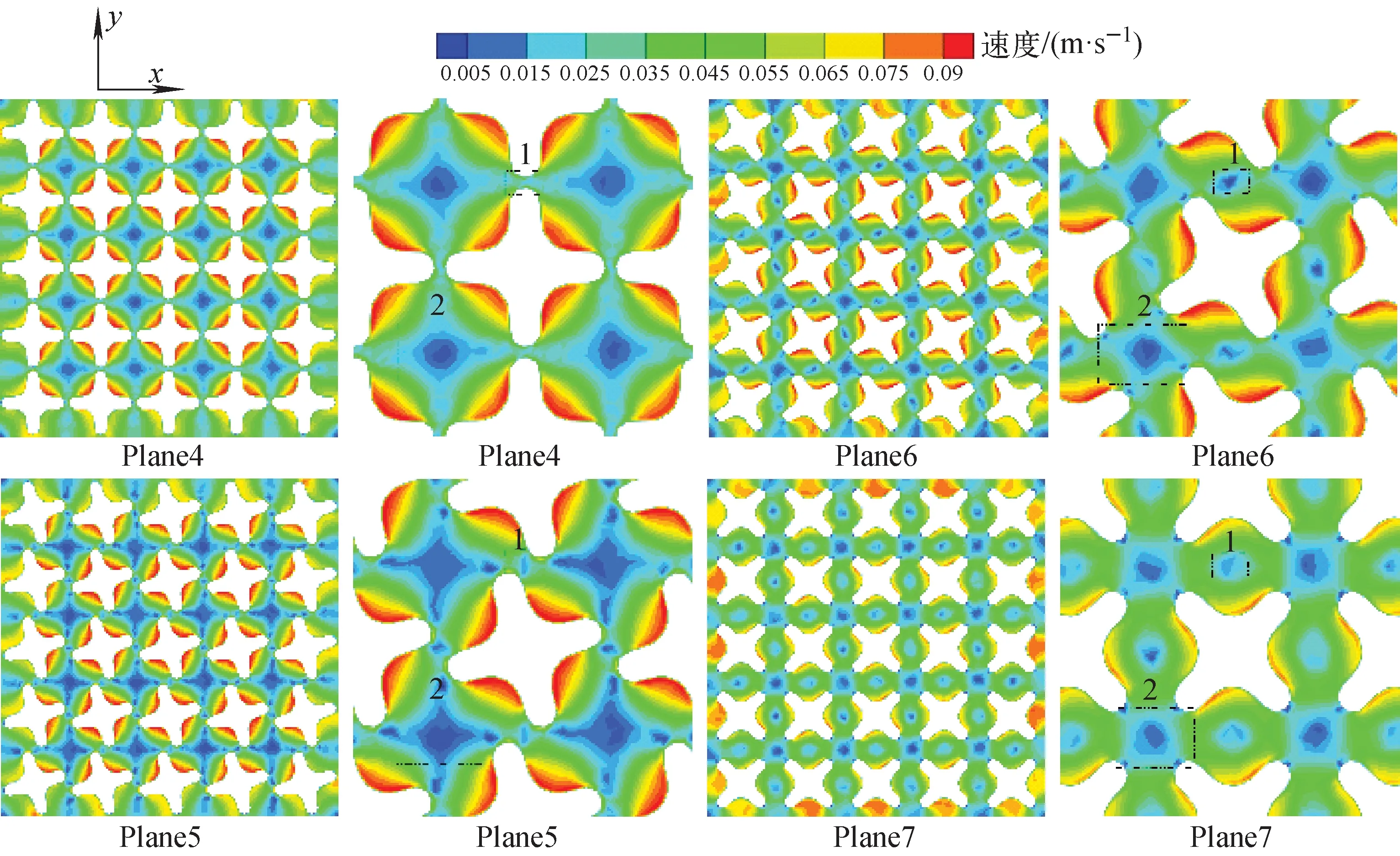
图7 不同高度截面二次流速度分布云图
图8示出相同节距、不同入口流速(工况1~4)燃料组件径向上截面Plane5二次流速度分布云图及局部子通道速度矢量图。图9示出Plane4不同入口流速的截面二次流速度。由图8可看出,入口流速从1.25 m/s增大至3 m/s的过程中,燃料棒近壁面处二次流速度逐渐增大,且截面平均二次流速度也不断提高,由图9可看出,截面二次流速度平均值从0.022 m/s增大至0.056 m/s,截面二次流速度随入口流速的增大而增大,二次流速度最大值出现在燃料棒近壁面区域,随流速的增大,最大值从0.048 m/s增大至0.115 m/s,二次流速度随入口流速的增大呈线性增长;二次流速度较低区域呈“十字”型分布,该区域的形状由各燃料棒间相对角度所决定,二次流速度最小值出现在子通道中心处。流体流过燃料棒表面,受到燃料棒自身的扭转结构影响,近燃料棒壁面处的流体扰动增大,产生二次流,有利于子通道内和各子通道间的流体交混。从局部速度矢量图可看出,由于燃料棒扭转方向为逆时针,近燃料棒壁面处速度矢量均为逆时针旋转;在相邻燃料棒的棒间隙内,会同时出现流动方向相反的两个区域,造成间隙内流体径向速度较低,二次流速度较低,造成这种现象的主要原因是,在间隙处,相邻燃料棒的螺旋方向正好相反;相邻4根燃料棒所围成的子通道由于燃料棒的共同影响,形成顺时针旋转的二次流,且二次流速度随远离燃料棒距离增大而减小。
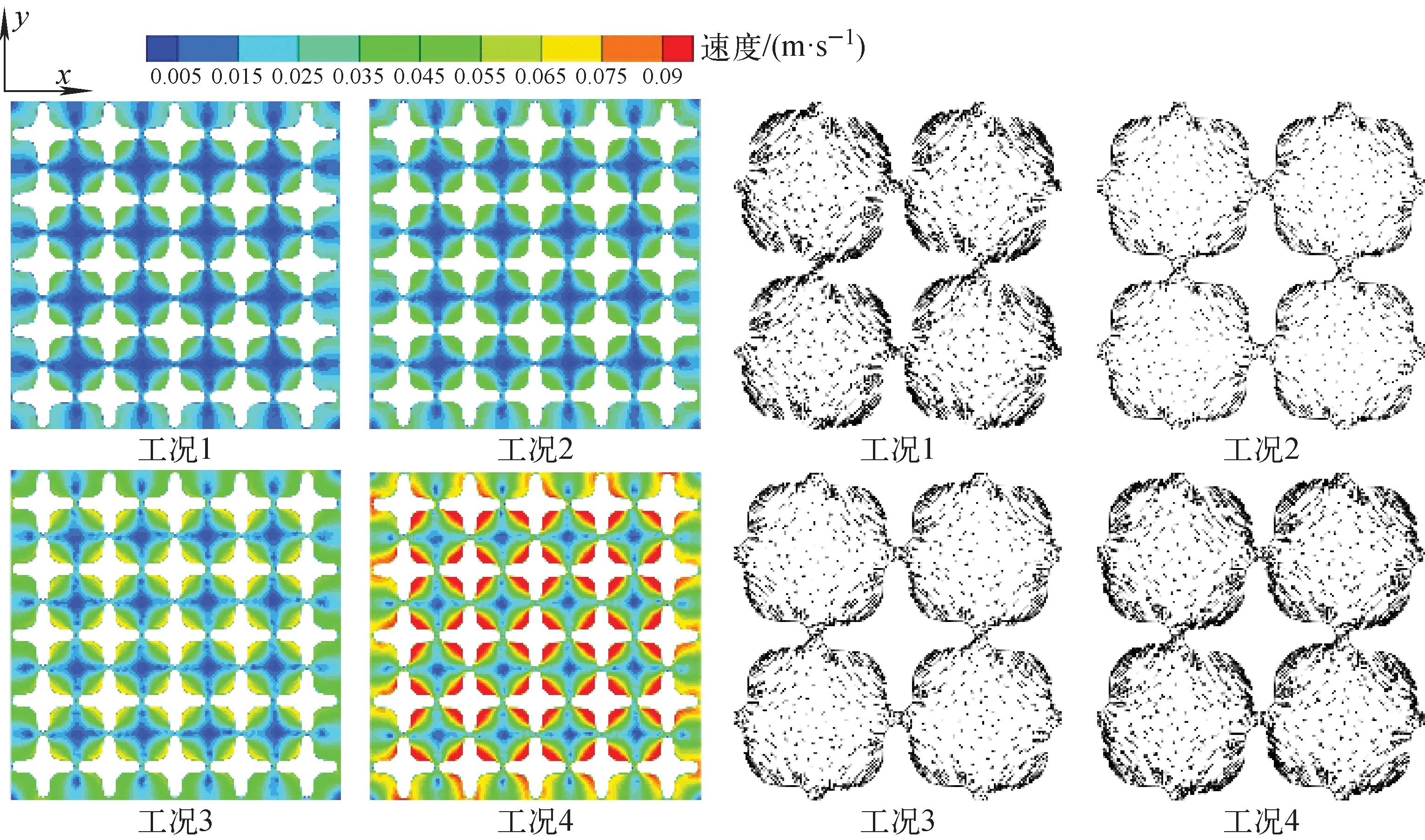
图8 不同入口流速Plane5上二次流速度分布云图及局部子通道速度矢量图

图9 不同入口流速的截面二次流速度
图10示出相同入口流速、不同螺旋节距(工况5~7)燃料组件径向截面Plane5二次流速度分布云图及局部子通道速度矢量图。图11示出Plane4不同螺旋节距的截面二次流速度。由图10可看出,随螺旋节距从H=250 mm增加至H=1 000 mm,燃料棒近壁面处二次流速度不断减弱,截面平均二次流速度也逐渐减小,由图11可看到,截面平均二次流速度从0.101 m/s逐渐减小至0.022 m/s,截面二次流速度最大值从0.909 m/s减小至0.049 m/s,各子通道区域由于远离壁面,受到的燃料棒结构的影响较小,故二次流速度较小。由此可知,螺旋节距减小,流体沿轴向流动时受到的扰动变大,交混程度提高,有利于带走燃料棒表面的热量,使流体温度分布更均匀。

图10 不同螺旋节距Plane5上二次流速度分布云图及局部子通道速度矢量图
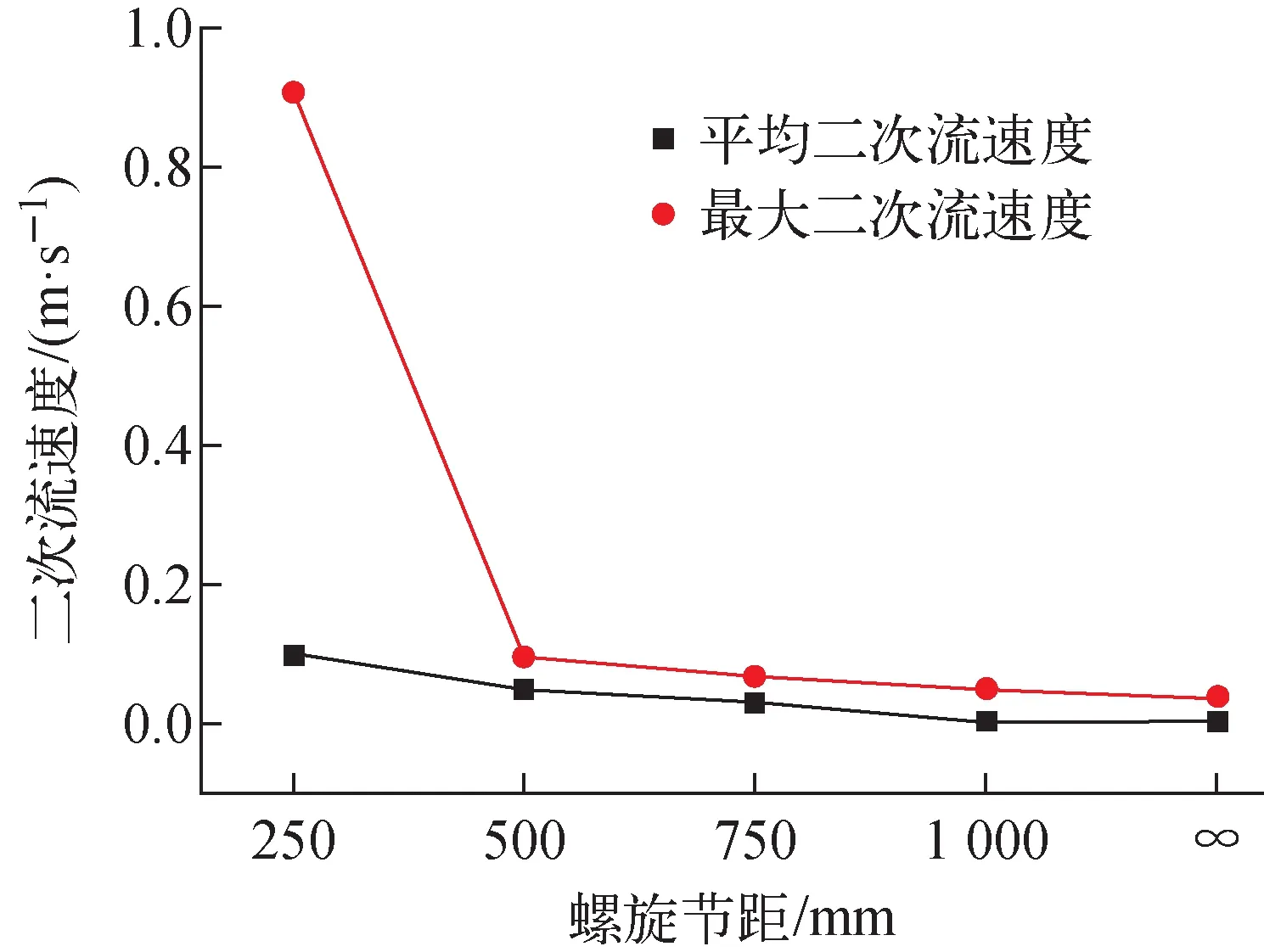
图11 不同螺旋节距的截面二次流速度
2.2 温度场分析
冷却剂沿燃料棒束轴向各截面Plane1~3上的温度分布云图如图12所示。由图12可看出,由于燃料棒自身扭转结构的存在,流体交混程度增加,各子通道内部温度分布均匀。流体自下而上流动的过程中,随着棒间隙逐渐增大,各子通道间的温度分布趋于均匀,随着棒间隙逐渐减小,各子通道间温度分布又趋于独立,间隙处温度高于子通道中心区域温度。靠近矩形通道壁面处的Plane3有局部热点的出现,而Plane1和Plane2温度分布较均匀,没有局部热点出现。
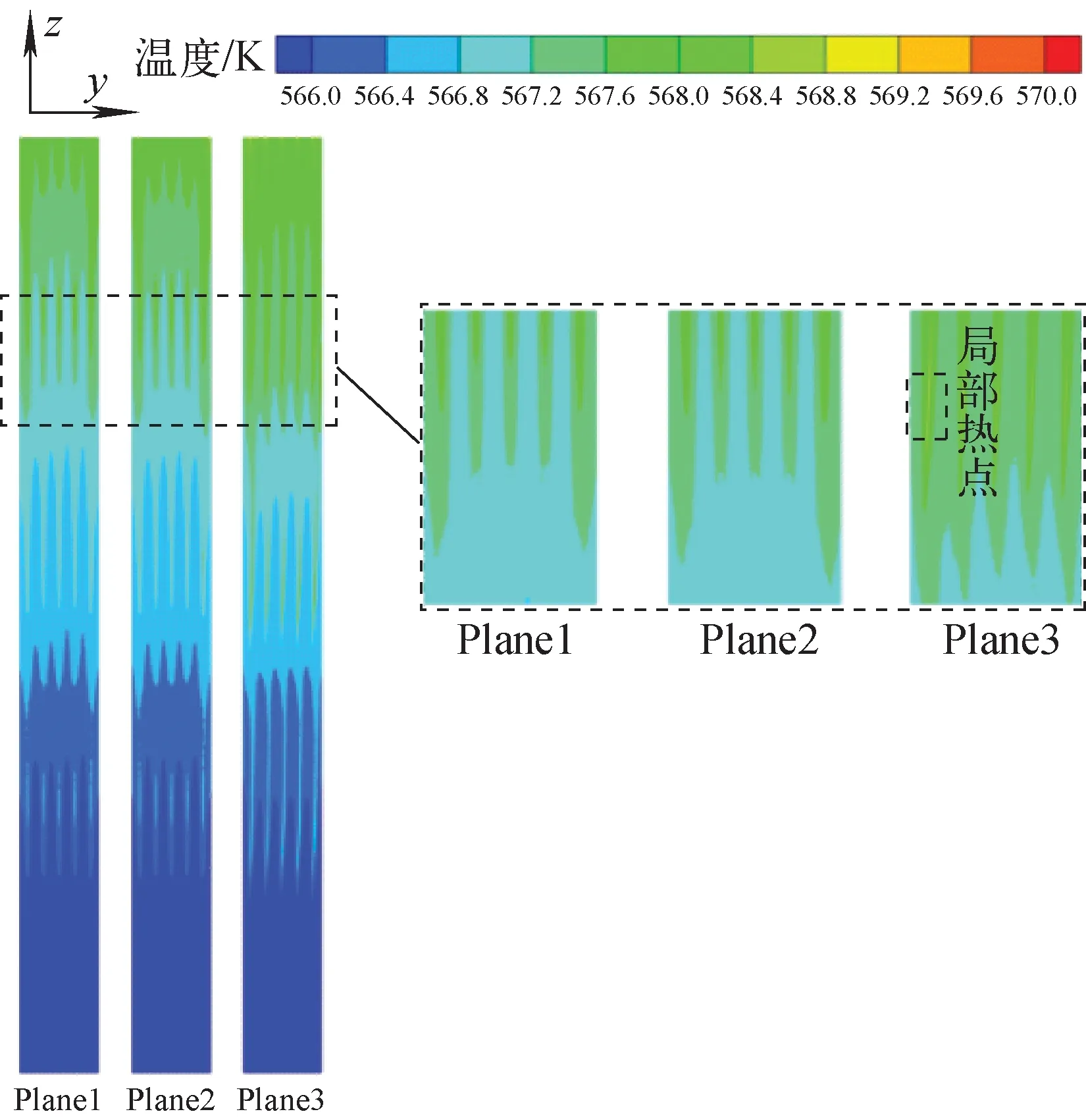
图12 燃料棒束轴向各截面Plane1~3温度分布云图
图13示出不同流速和不同螺旋节距轴向截面Plane1的温度分布云图。由图13a可看出,冷却剂自下而上流动的过程中,入口流速越低,流体出口温度越高,温度分布越不均匀。由图13b可看出,燃料棒节距从H=250 mm增大至H=∞,流体出口温度基本不变,为568.62 K左右,各子通道间流体温度分布均匀程度呈周期性变化,这与燃料棒的扭转周期一致。

a——不同入口流速下温度分布;b——不同螺旋节距下温度分布
图14示出工况5燃料棒表面温度和轴向截面温度分布云图。由图14可看出,燃料棒束表面温度沿流动方向呈螺旋状分布,燃料棒外凸弧区域温度低于内凹弧区域,且沿流动方向外凸弧区域温度升高速度低于内凹弧区域。从轴向截面温度分布云图可看出,燃料棒外凸弧区域温度显著低于燃料棒中心温度,在外凸弧处低温区呈偏心分布,沿燃料棒扭转方向(逆时针)温度逐渐降低。在不同截面处燃料棒内部温度分布规律基本一致。造成这种现象的原因是外凸弧处相对于内凹弧处散热面积更大,外凸弧区域远离燃料棒中心,且流体沿轴向流动的过程中在内凹弧处流体速度降低,致使该处热量难以被流体带走,造成内凹弧处温度沿流动方向上升速度快于外凸弧处。

图14 燃料棒表面温度和轴向截面温度分布云图
图15示出不同入口流速时中心燃料棒在z=0.25 m(Plane4)处表面温度和表面努塞尔数沿圆周方向的变化。由图15可知,燃料棒表面温度沿周向呈周期性变化,周期数与燃料棒外凸弧个数相同,最高温度与最低温度分别出现在内凹弧部分和外凸弧部分周向角较小处。由图15b可看出,入口流速从1.25 m/s增大到3.0 m/s的过程中,燃料棒表面最大温度从582.4 K降低到574.4 K,表面温差ΔT从9.2 K下降至5.7 K,燃料棒表面平均温度降低,表面温差也减小。由图15c可看出,表面努塞尔数沿周向也呈周期性分布,分布规律与温度一致;外凸弧部分努塞尔数高于内凹弧部分,最大值和最小值出现位置与温度分布相反,随入口流速的增大,努塞尔数最大值和最小值的差值也逐渐减小。

a——周向角度定义;b——周向温度分布;c——周向努塞尔数分布
不同轴向位置处冷却剂温度分布云图如图16所示,同一截面上的流体温度分布不均匀,近壁面处流体温度显著高于子通道中心位置的流体温度。随着流体沿轴向流动,外凸弧部分周向角较大处温度的升高速率要高于周向角较小处的升高速率,这是由于相邻两个外凸弧之间的流体在流经周向角更大的外凸弧时,流动阻力增大,停留的时间更长,吸收的热量更多,故温度升高速率更大。在不同轴向截面处,燃料棒近内凹弧区域的水温均高于子通道中心区域的水温,主要是因为前者的位置距离燃料棒表面更近。

图16 不同轴向位置处冷却剂温度分布云图
2.3 换热系数分析
图17示出不同流速下燃料棒束沿程换热系数的变化。在同一入口流速下,由于入口效应的影响,在入口处换热系数较高。随着流体流动,入口效应的影响逐渐减小,换热系数也逐渐降低;当流体流过一定距离后,局部换热系数逐渐平稳。当流体沿轴向继续流动,换热系数偶有波动但总体趋势平稳。随着入口流速的增加,沿程换热系数逐渐增大,换热得到了增强。因此,通过增加入口流速可增强棒束表面的换热性能以及棒束内的流动交混,降低燃料棒表面的温度和周向温度分布的不均匀性。

图17 不同入口流速下燃料棒束沿程换热系数变化
图18示出不同螺旋节距下燃料棒束沿程换热系数的变化,在同一节距下,由于入口效应的影响,在入口处换热系数较高。随着流体流动,入口效应的影响逐渐减小,换热系数也逐渐降低,与同一入口流速的变化趋势一致;节距为H=250 mm的沿程换热系数最高,随着螺旋节距的增大,沿程换热系数不断减小,但节距为H=∞的沿程换热系数与H=750 mm的换热系数相近,且高于节距为H=1 000 mm的换热系数。因此,增加燃料棒的螺旋节距会降低燃料棒束的换热性能,螺旋节距大于等于H=750 mm时,燃料棒束的换热性能与无扭转的燃料棒(H=∞)相差不大,甚至更低。
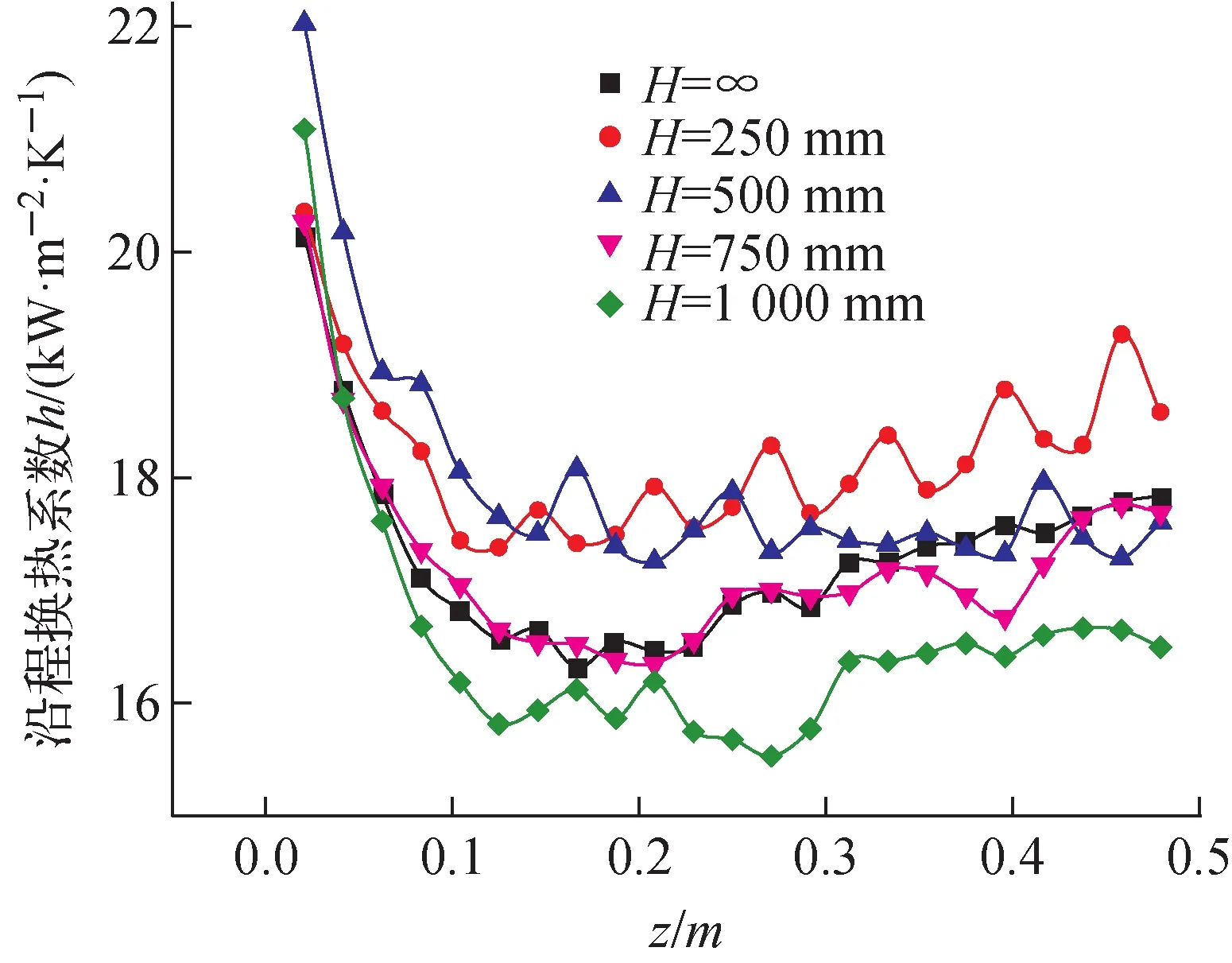
图18 不同螺旋节距下燃料棒束沿程换热系数变化
3 结论
本文针对5×5花瓣形燃料组件开展单相流动与换热特性数值模拟,获取速度场、温度场、换热系数等热工参数,分析速度(即雷诺数)和几何参数对棒束组件流动换热特性的影响,得到如下结论。
1) 花瓣形燃料棒自身的螺旋结构可增强冷却剂在棒束间的横向流动,近燃料棒壁面区域的二次流速度与燃料棒自身结构相关,内凹弧区二次流速度高于外凸弧区;子通道中心区域由于远离燃料棒壁面,二次流速度很低。
2) 在同一高度处,燃料棒表面温度和努塞尔数沿周向呈周期性变化,周期数与花瓣数一致,且内凹弧处的温度要明显大于外凸弧处的温度。随着冷却剂沿轴向不断流动,外凸弧部分周向角较大一侧水温的升高速率要高于较小一侧的升高速率。
3) 换热系数沿流动方向先降低,之后逐渐平稳;随着入口流速的增加,棒束表面的换热性能及棒束内的流动交混逐渐增强,燃料棒表面温度沿轴向和周向分布的不均匀性逐渐降低,燃料棒束沿程换热系数增大。
4) 螺旋节距不同,沿程换热系数也不同,燃料棒束沿程换热系数随节距的增大而减小,当节距H大于750 mm后,燃料棒束换热系数与无扭转的燃料棒(H=∞)相差不大,甚至更低。

