超临界流体物性畸变特性的多尺度研究

刘旻昀，黄彦平，唐 佳，臧金光，赵学斌，黄善仿，何茂刚，张 博

(1.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室，四川 成都 610213；2.清华大学 工程物理系，北京 100084；3. 西安交通大学 热流科学与工程教育部重点实验室，陕西 西安 710049；4.大连理工大学 能源与动力学院，辽宁 大连 116024)

超临界流体的热物理性质在其临界点和拟临界线附近会发生剧烈变化，由于这种独特的物性畸变特性，萃取和化学合成领域可通过细微的温度压力调节使物质的溶解度发生几个数量级的突变，以达到使分离物析出或控制反应的目的[1]。在超临界二氧化碳布雷顿循环中，通常将压缩机进口温度设置在拟临界温度附近，利用密度的畸变特性降低压缩功、提高系统效率[2-3]。然而，在超临界水动力循环或超临界碳氢燃料热管理系统中，超临界流体的物性畸变特性还可能诱发传热恶化使得壁面过热失效[4]。因此，为保障和优化超临界流体在能源动力、传质萃取、化学反应、环境治理等领域的应用，必须对超临界流体物性畸变特性进行深入研究。目前，关于物性畸变机理的认识尚未统一。一种观点[5-7]认为，拟临界现象与亚临界气液相变物性变化特点相近。在拟临界现象发生时，超临界流体内部存在类气结构与类液结构之间的转变，转变过程仍可用超临界气液共存和拟沸腾来描述。另一种观点[8-9]将拟临界现象视作临界现象的延伸，强调体系内部涨落的影响。第三种观点[10]则不考虑拟临界现象本身的特殊性，在研究相关问题时看作物性剧烈变化的单相流体。但上述3种观点均没有严格的理论支撑，同时也无法给出超临界流体发生物性畸变的根本原因。

从描述短程相互作用的分子作用力，到描述长程关联的有序结构，再到宏观上表现出的均一相态，超临界流体物性畸变特性存在于微观、介观和宏观的不同尺度上。在微观尺度上，光散射和中子散射实验[11]为研究体系的微观结构变化特点提供了有力手段，而分子动力学[7,12]等模拟手段则作为一种更廉价而精细的补充。在介观尺度上，对于临界现象，标度理论[13]和重整化群理论[14-15]从标度不变性出发，用粗粒化的思想建立了完整的理论描述；而对于拟临界区物性畸变，尚未有理论提出。在宏观尺度上，关于超临界流体传热异化的研究[16]已有很多，但在拟临界区物性计算方面，如今应用最为广泛的NIST数据库[17]也有较大偏差。针对上述问题，本文从微观、介观和宏观尺度对超临界流体的物性畸变特性进行全面分析。采用分子动力学模拟复现和研究超临界二氧化碳在拟临界区的物性畸变特点；提出一种考虑外场的气液相变模型，补充拟临界现象认识上的理论空白，同时结合标度理论，推导部分物性在趋于临界点时的发散规律；开展高精度的二氧化碳密度、定压比热、黏度物性测量实验，指出现有计算模型的缺陷。

1 分子动力学模拟

本文采用Material Studio软件中的分子动力学模拟功能，研究二氧化碳流体体系跨越拟临界点时的微观结构特性。

1.1 计算模型

力场模型为COMPASS力场[18]，其在单分子或凝聚态物质结构、热力学性质等方面的预测能力已得到广泛证实。模拟体系为立方体盒子，在x、y、z方向上均采用周期性边界条件以消除边界效应。根据分子数量、截断半径无关性、时间步长无关性的检验结果，同时尽可能减小计算资源的消耗，设置二氧化碳分子数为256，截断半径为1.55×10-9m，时间步长设为7×10-16s。

在模拟过程的前3×10-10s，保持体系的粒子数、体系体积及温度不变(即正则系综)，使得体系达到迟豫平衡。此时，模拟结果的统计量收敛到一个准稳态，而与分子的初始排布方式无关。然后，保持体系的粒子数、体系压力和温度不变，对体系的密度、双体分布函数、配位数、静态结构因子等物理量进行统计。模拟过程中的温度控制方法为Berendsen控温法(即恒温热浴耦合法)，压力控制方法为随机碰撞法。对于分子之间的非键相互作用，采用Group-Based加和方法进行求解。另外，还可根据能量波动方法求得定压比热，通过统计体系内粒子数目的波动求得等温压缩系数等[19]。

1.2 计算结果

图1为5 MPa下二氧化碳密度的分子动力学模拟结果与NIST数据库值之间的偏差。可看出，分子动力学模拟能准确预测流体的密度，同时很好地捕捉到该压力下的气液相变点，最大相对偏差仅为5.46%。进一步对7.38 MPa和16 MPa下的二氧化碳密度进行了模拟和对比，结果表明：对于远离临界点的状态，分子动力学模拟方法在预测流体密度时精度较高，模拟值与数据库值的相对偏差小于5%；在临界点附近计算偏差显著上升，但仍有相同的变化趋势。因此，本文所搭建的分子动力学模型可作为定性研究物性畸变现象的手段。

图1 5 MPa下二氧化碳密度模拟结果与NIST数据库值的对比

以双体分布函数g(r)为工具，研究体系的微观特性。作为分子排列有序性的一种度量，g(r)表示以一个任意指定的粒子为中心，在距离r处找到其他粒子的概率。图2为7.38 MPa下T=280～350 K的二氧化碳体系的C-C原子双体分布函数的变化情况，作为对比，图2中虚线分别为280 K、0.1 MPa下二氧化碳和氦气的g(r)曲线。从图2可看出，随温度的升高，双体分布函数的第1峰与第2峰之间的峰谷逐渐升高，说明体系的有序程度不断减弱、分子排列变得稀疏。当温度高于310 K后，g(r)曲线中仅存在第1峰，而第1峰之外，与280 K、0.1 MPa下的气态二氧化碳情形十分相似。这说明体系中仅存在严格的近程有序，体系的微观状态更接近于气态。但与氦气情形下的近程无序且长程无序不同，二氧化碳在气态条件下仍是近程有序的，这实际上反映了二氧化碳分子不为0的四极矩之间的相互作用。当温度小于304.13 K或大于305 K时，体系的g(r)曲线基本重合；而在304.13～305 K的温度区间内，曲线特征发生显著的转变。

图2 7.38 MPa下T=280～350 K时C-C原子间双体分布函数对比

对于一定压力下的超临界流体，温度较低时体系的有序程度较高，表现为近程、中程有序而长程无序，与液体类似；温度较高时体系表现为近程有序而中长程无序，与气体相似；在中间的某一狭窄温度区间内，体系的结构发生剧烈的变化。因此，可进一步将超临界流体区划分为类气区、类液区和拟临界区，这与散射实验[11]的测量结果也是吻合的。

2 考虑外场的气液相变模型

分子动力学模拟从微观视角上给出了拟临界现象的直观认知，但仍无法解释超临界流体发生拟临界现象的原因。为解释这一问题，本文基于朗道二级相变理论[20-21]和标度理论，提出一种考虑外场的气液相变模型。

2.1 考虑外场的朗道模型

根据朗道理论在其他体系的推广形式[22-24]，如描述液晶体系相变的Landau-de Gennes模型[25]，本文提出了一种新模型。在新模型中，序参量η为(ρ-ρc)/ρc，其中ρ为流体的平均温度，下标c表示临界点状态。在这种定义下，η在整个流体域均有明确的定义，且在临界等容线(ρ=ρc)上等于0。此外，朗道理论中热力学势Φ的表达式也按实际流体的特性进行了改进。首先定义一组无量纲变量(p,t,η)，其中p=(P-Pc)/Pc为无量纲压力，而t=(T-Tc)/Tc为无量纲温度。新的热力学势表达式为：

Φ(p,t,η)=Φ0(p,t)+C(-(p-bt)η+atη2+Bη4)

(1)

式中：a、b、B、C均为大于0的系数，b、C为常数，a、B仅与压力相关；Φ0(p,t)为与流体温度和压力相关的常规项。

相比于经典朗道理论，新模型基于重新定义的序参量η，同时增加了η的一次项。此一次项表示了外场h=p-bt对热力学势的作用，也对应于温度和压力对于流体状态的影响。根据朗道理论，一个稳定的热力学状态(p,t)对应于(∂Φ/∂η)p,t=0，由式(1)则有：

h=p-bt=2atη+4Bη3

(2)

因此，对于临界等容线η=0，流体的压力与温度应满足线性关系(图3)。无论是对于水、二氧化碳、氮气还是氧气，不同流体的临界等容线均在很大的温度压力范围内保持线性，进而证明了引入的线性外场项的正确性。

图3 4种不同流体的临界等容线

由式(1)的热力学势表达式可推导出流体的定压比热cp为：

cp=T(∂s/∂T)P

(3)

(4)

由式(4)可知，定压比热cp由常规项cp0和拟临界增强项两部分构成。在拟临界区，密度随温度的剧烈变化导致拟临界增强项的增加。图4以23 MPa下的超临界水对式(4)进行了验证。可看出，在接近临界密度时，定压比热的畸变与∂ρ/∂T的变化高度相关。

图4 临界等容线附近超临界水的定压比热畸变规律

2.2 考虑外场的标度理论

除了可在定量上解释拟临界区的物性畸变特性，本文所提出的模型亦适用于亚临界气液相变。但对于临界点邻域，模型的预测值与实验测量值存在显著的偏差。以临界等温线和临界等压线为例，则：

(5)

对应的临界指数δ=3与实验测量的结果δ=4.8±0.02不相符。针对此问题，标度理论和重整化群理论的结论为：在临界点附近，体系内部涨落的影响不可忽略，导致忽略了涨落的朗道理论不再适用。此时不能遵循平均场近似，需考虑体系内部剧烈涨落对热力学势的影响，因此有必要对模型在临界点邻域进行修正。根据标度理论，趋于临界点时体系的关联长度发散，此时系统具有标度不变性，热力学函数可转换为系统参数的广义齐次函数f。对于外场影响下的序参量，则：

(6)

式中：±分别对应η>0和η<0；β为热膨胀系数。

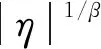
(7)

3 超临界二氧化碳高精度物性测量实验

在宏观尺度上，目前超临界二氧化碳拟临界区热物理性质实验数据稀少，且不同来源实验数据间的一致性也较差。因此，本文联合西安交通大学和大连理工大学开展了两组“背靠背“的物性测量实验进行验证。以二氧化碳为实验工质，分别采用U型管振荡法[26]、流动型量热法[27-28]、毛细管法[29]，完成25～500 ℃温度范围、7～14 MPa压力范围内的密度、定压比热和黏度的测量，共得到数据点1 940个，图5为实验装置示意图。表1列出在置信因子k=2、置信度为95%的条件下两组实验中压力、温度、定压比热及黏度的测量不确定度。

表1 物性测量实验的不确定度

a——定压比热实验测量系统；b——黏度和密度实验测量系统

从“背靠背”验证的角度来看，在相同工况下，两组密度测量结果的平均相对偏差仅为0.127%，吻合较好。将实验结果与当前应用最为广泛的Span-Wagner方程[30]和Vesovic黏度计算模型[31]的计算结果进行对比，对于物性变化较为平缓的一般区域，实验结果与计算结果的偏差很小(表2)。但对于物性剧烈变化的拟临界区，实验结果与计算结果的偏差显著增大，且表现出物性畸变越剧烈则偏差越大的趋势(表3)。现有的拟临界区数据点仍较少，数据点压力偏高且温度间隔过大，实验精度需进一步评估和优化。

表2 一般区域内实验测量结果与计算结果的相对偏差

表3 拟临界区部分实验测量结果与计算结果的偏差

现有的二氧化碳热物理性质理论模型在拟临界区之外计算精度较好，但在近临界区仍存在缺陷，计算精度需实验验证并进一步提高。对于超临界二氧化碳布雷顿循环，为了获得更高的系统效率，往往需要尽可能将背压设置得低(如7.4 MPa)，利用这种畸变特性来减小压缩功。因此，掌握二氧化碳热物性在近/超临界区域精确的实验数据及其变化规律是一个关键问题，需要在实验技术、理论模型等方面进一步研究。

4 超临界流体区的严格划分

通过微观、介观、宏观3个不同尺度的研究分析，得到超临界流体发生物性畸变的机理。分子动力学模拟的结果表明，超临界流体在拟临界区发生物性畸变时，同时伴随类气-类液结构之间的转变，而在涨落主导的临界点邻域内，流体分子之间存在长程关联。长程关联带来的体系自相似性为采用粗粒化方法建立标度理论提供了依据，但也导致传统连续体假设的失效。因此，研究处于临界点邻域的流体必须从更为基础的假设出发，采用分子动力学模拟或格子玻尔兹曼方法[32]。随着远离临界点，涨落迅速衰减以至于可忽略，此时基于平均场思想的朗道理论变得适用。同时由于不存在长程关联，传统的宏观描述(如Navier-Stokes方程)同样成立，但需注意物性畸变对于流动、传热等宏观行为的影响。因此，超临界流体区域可进一步划分为4个子区域(图6)：临界点邻域、类气区、类液区和拟临界区。

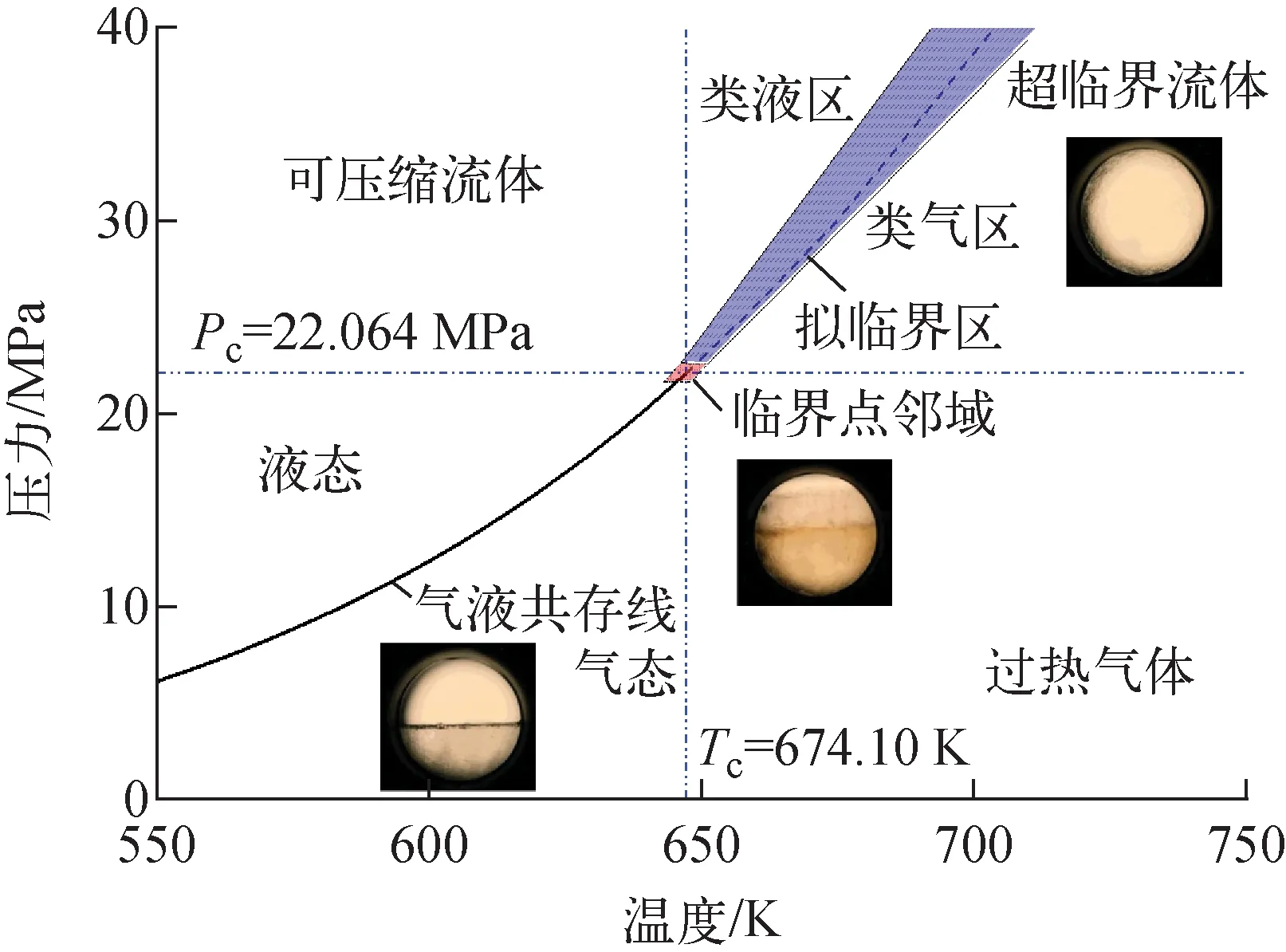
图6 临界等容线附近超临界水的定压比热畸变规律

关于各区域的划分，首先可估算临界点邻域的范围。当沿临界等容线趋近临界点时，关联长度ξ的发散遵循[33]：

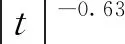
(8)

当|t|足够大时，流体分子之间无长程关联，而只有分子间作用力决定的短程关联，因此ξ≈ξ0≈10-10m。只有当t≈10-6时，关联长度才会增长到与流体层厚度相当的μm量级。对于二氧化碳，t≈10-6对应于T-Tc≈3×10-4K。因此，临界点邻域的范围是很小的。对于大部分的超临界流体应用场景而言，传统的宏观描述均适用。对于其他3个区域，Banuti[34]推广了亚临界条件下的克拉伯龙方程，得到关于超临界流体的划分方法；Kurganov等[35]则从流体压缩性的评估出发，以相对膨胀功Eq=pβ/ρcp作为划分依据。总地来说，拟临界区的划分更多是经验性的，因此两种划分方法都可行。在实际工程中，为了使用方便，也可根据第2节中的结论，以无量纲密度作为划分拟临界区的简单判据。

5 结论

本文通过微观、介观和宏观3个不同尺度的分析论证，发现了导致超临界流体物性畸变的不同机制。根据影响机制的不同，在相图上，超临界流体区可进一步细分为临界点邻域、拟临界区、类气区和类液区，得到如下结论：1) 分子动力学模拟的结果表明，在跨越拟临界线时，超临界流体的微观构型会发生类气-类液之间的转变；2) 在临界点邻域内，体系的热力学函数、涨落和关联长度趋于临界点时按幂律发散，此时考虑外场的标度理论可很好地描述，但传统的宏观描述和平均场理论均失效；3) 临界点邻域的范围很小，以无量纲温度t=(T-Tc)/Tc表示时，近似满足t<10-6；4) 对于绝大部分工程应用场景，超临界流体内部的涨落影响均可忽略，此时考虑外场的气液相变模型能很好地描述物性畸变的规律；5) 无量纲密度|η|<0.25可作为划分拟临界区的简单判据，对于二氧化碳，对应密度为350～585 kg/m3；6) 超临界二氧化碳的物性测量实验结果表明，现有的物性模型在描述拟临界区物性畸变特性方面仍有不足，但对于拟临界区之外的一般区域已有足够高的计算精度。