基于Matlab的模型预测控制仿真与性能分析

陈洪科

(厦门大学嘉庚学院 信息科学与技术学院，福建 漳州 363105)

0 引言

自上世纪七十年代被提出以来，预测控制算法因其优良特性在复杂工业过程控制中得到广泛应用。经过40年来的发展与应用，该类算法已经从线性、时不变、单变量系统的预测控制发展为非线性、时变、多变量系统的预测控制，极大地拓展了应用领域。近年来，预测控制的思想和方法在电力电子、航空航天、能源、采矿、农业等诸多领域得到应用，表现出强劲的生命力。

在电力电子领域，电力电子变流器具有非线性、变结构的特点，传统控制器难以获得理想的性能[1]，连续控制集模型预测控制和有限控制集模型预测控制算法被用于此类系统控制，发展前景广阔。而针对互联电力系统的分布式控制，分布式模型预测控制（Di-MPC）采用本地局部优化控制和全局协同控制相结合的策略，局部控制故障不会影响全局系统运行[2]，应用优势明显。在船舶航运领域，针对船舶运动过程中的大惯性、长时滞、非线性等特点，预测控制算法能够运用在动力定位系统控制、减摇水舱控制和航向航迹控制等方面[3]。在农业领域，模型预测控制算法（MPC）可应用于农机协同控制。针对协同作业跟随农机行驶工况不稳、跟随协同响应慢、控制困难等问题，采用两层控制架构，上层基于模型预测控制算法获得控制加速度的最优控制目标，下层则基于前馈与PI反馈实施控制，跟随效果良好[4]。在新能源领域，MPC算法被用于波浪能转换装置控制以提高海洋表面波浪运动能量的提取效率。这一应用问题本质上是一个约束优化问题，模型预测控制器能输出最优化控制量，并与当前波浪作用力作为转换装置的输入实施最优控制[5]。在采矿领域，MPC算法被用于瓦斯抽采智能控制[6]。首先通过对瓦斯抽采系统进行分析和建模，建立了瓦斯抽采智能调控模型，将瓦斯抽采浓度、纯量、负压及抽采泵效能比作为被控量，将抽采钻孔的阀门开度和抽采泵功率作为控制量，利用MPC对控制量进行智能控制。为了获得被控量目标值，采用了简单循环神经网络分析和学习被控量历史数据的时间变化规律，进而得到被控量的时间变化拟合曲线。经实践应用证实，MPC算法能够使被控量很好地跟随参考值，且能克服环境及非线性因素的干扰，调控效果良好。

预测控制算法的广泛应用证明了其有效性。本文首先对模型预测控制算法理论进行介绍，然后通过仿真讨论其算法特征与控制性能的关系。

1 模型预测控制算法

预测控制算法根据预测输出和期望输出来计算控制量。给定设定值r，被控对象当前时刻（k=0）的输出值到给定值的期望转移过程用yr(k)表示。由已知的被控对象模型可以预测对象在未来P个时刻的输出，记为yM(k)(k=1, 2, ..., P)。预测控制算法以预测输出与期望输出的偏差e(k)为最小化优化目标，由此计算出当前及未来共计L个时刻的控制量u(k)(k=0, 1, 2, ..., L-1)。模型预测控制算法是一种基于模型的优化控制算法，由预测模型、模型校正、参考轨迹和滚动优化四个部分组成，如图1所示。

图1 模型预测控制算法组成

1.1 模型预测与反馈校正

设被控线性对象的单位脉冲响应采样值为h1, h2,…，则其输入输出关系可以表示为

对于渐近稳定对象，阶跃响应在某一时刻k=N后趋于平稳，即有hN+1=hN+2=…=0，所以对象的动态信息可以用有限集合{h1, h2, ..., hN}加以近似描述。那么，该对象的预测模型可以表示为

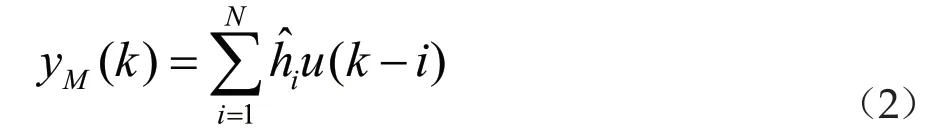
由此可得被控对象在P个预测步程内的预测输出为

式中，i=1, 2, ..., P。

在式(3)的基础上进一步考虑模型误差和干扰，采用前一时刻预测值与实际值的偏差来校正预测模型，同时采用校正后的预测值代替实际测量值，则有式中，i=1,2, ..., P。将校正后的模型预测结果记为向量形式yc =[ yc(k+1), yc(k+2), ..., yc(k+P)]T。

1.2 参考轨迹

为使输出变量平稳过渡，被控对象的期望输出是从当前时刻的实际输出y(k)到设定值光滑过渡的一条参考轨迹。在k时刻的参考轨迹可由其在未来采样时刻的值yr(k+i) (i=1, 2, ...)描述，通常取一阶指数函数形式，即有

式中，τ是参考轨迹的时间常数，T是采样周期。令α=e -T/τ，则有

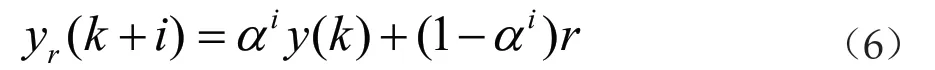
可见，τ值越小，α（0≤α≤1）值越小，参考轨迹能越快地到达设定值r。参考轨迹亦可以简记为矩阵形式，即

式中，yr =[ yr(k+1), yr(k+2), ..., yr(k+P) ]T，α1 =[ α, α2, …, αP ]T，α2 =[ 1-α, 1-α2, …,1-αP ]T。

1.3 滚动优化

根据前述模型预测和参考轨迹的向量形式，可以写出二者误差的向量形式，即有e=yr - yc。滚动优化的目的是在每一步控制中，找到当前到未来由近及远的L个时刻的控制量，使未来P个时刻的预测输出尽可能地接近参考轨迹。因此，优化目标函数可以表示为：

式中，Q1和Q2是系数对角矩阵，Q1=diag{q2 11, q2 12, ..., q2 1P}，Q2=diag{q2 21, q2 22, ..., q2 2L}。对于多输入多输出（MIMO）系统，还需考虑不同变量之间的权重[7]，优化目标函数为

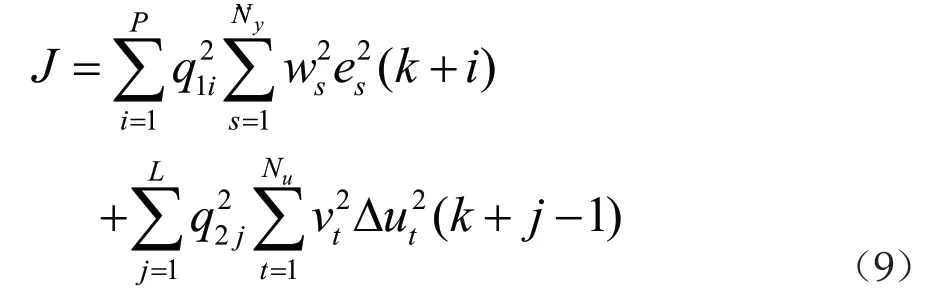
式中，Nu和Ny分别是控制变量、输出变量的个数，ws和vt表示权重。求解∂J / ∂Δu=0即可得到所需的控制增量Δu。

2 算法仿真与性能分析

借助Matlab软件的模型预测控制工具箱（Model Predictive Control Toolbox）可以方便地进行模型预测控制算法的仿真。该工具箱提供了GUI界面，可以对被控对象、MPC控制器和仿真条件进行建模或设置，其中控制器的设置包括基本的步程信息、变量约束、权重调整和干扰信号估计等，仿真条件则包括被控对象、控制器、开/闭环、参考值、不可测干扰等。该工具箱也支持代码模式。

本文以连续搅拌釜式反应器作为被控对象实施仿真，示意图如图2所示。CAi、Tc、T、CA分别为进料反应物浓度、冷却液温度、反应器内部温度和釜内主要反应物浓度。显然，CAi、Tc属于输入变量，T、CA属于输出变量。但由于反应物浓度通常难以测量，因此将CAi、CA分别定义为不可测干扰、不可测输出，Tc和T则分别是控制量和可测量输出。

图2 连续搅拌釜式反应器模型

该反应器的线性化状态空间模型为：

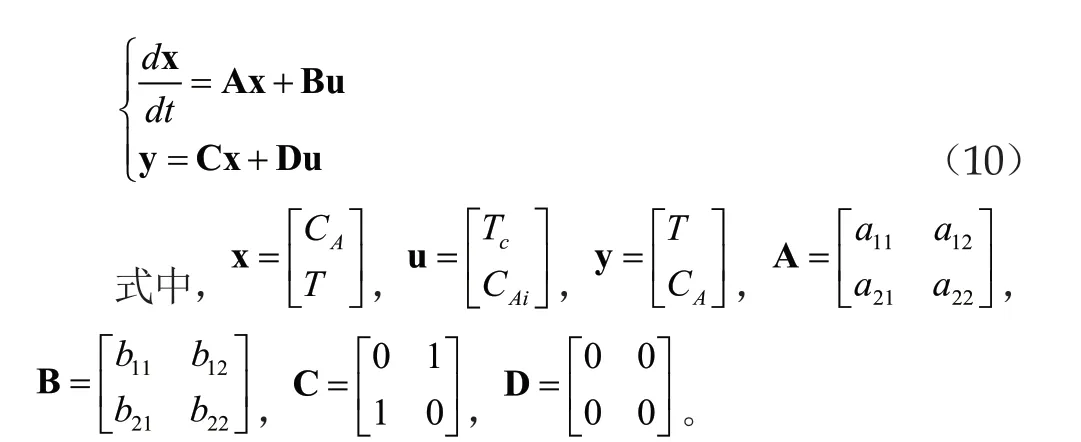
2.1 变量权重

为了考察输入变量、输出变量权重对控制性能的影响，以表1所示两组权重进行仿真和对比。仿真结果如图3所示。

图3 不同变量权重仿真结果

表1 变量权重参数

反应器对象包含一个控制变量Tc和两个输出变量T、CA。在A组权重中，两个输出变量权重均为1.0，这表示对二者实施均衡控制，即都尽可能接近设定值。然而由于只通过一个控制变量实施控制，因此很难保证这一控制目标。在图3(a)中，可以看到两个输出变量均偏离设定值，无法取得预期控制效果。在B组权重中，仅输出变量T的权重为1.0，而CA的权重为0.0，这表示优先保证T的控制效果。在图3(a)中，可以看到反应器内部温度T能够正确跟随设定值变化，而反应物浓度CA则偏离了零值。

输入变量权重用于控制输入量与初始值保持一致，适用于输入量个数多于输出量个数的情形。本文所示仿真例不属于这种情况，因此将该权重设置为0.0，即输入量无需跟随初始值。输入变量变化率权重则用于限定输入变量变化率的大小，如式(9)中的vt所示——当增大vt时，在最小化J的前提下，控制增量Δu势必会减小；反之，Δu会增大。在图3(b)中，可以看到B组中冷却液温度Tc的增量绝对值大小比A组小，这便于控制动作的施行，但带来的影响是输出变量的上升时间增大。

2.2 变量约束

模型预测控制算法可以对变量设置约束，使之更符合实际被控对象或被控过程的物理属性。在表1中B组条件基础上，对控制量Tc及其增量分别设置[-10, 10]、[-3,3]的变化范围约束，仿真结果如图4所示。从图中可以看出，Tc的最大值被限制在了10，其每一步的变化量也未超过3，约束设置起到了作用。但与图3(a)相比可以发现，限制控制变量后会导致输出变量的上升时间增长，对控制性能有一定影响。

图4 具有变量约束的仿真结果

2.3 干扰建模与估计

在模型预测控制算法中，有三类干扰信号，包括不可测输入干扰、不可测输出干扰以及可测噪声。算法允许对被控对象受到的干扰与噪声进行预先估计和建模，以便使控制器更符合实际工况，提高控制性能。

针对釜式反应器给定两个控制器设计：控制器A将不可测输入干扰（进料反应物浓度CAi）建模为幅度为1的阶跃信号，控制器B则将输出变量之一的反应器内部温度T的不可测输出干扰建模为幅度为1的阶跃信号。二者分别在不可测干扰CAi为单位阶跃信号的条件下仿真，结果如图5所示。从图中可以看出，当单位阶跃干扰信号CAi出现时，两个控制器控制下的输出变量均会发生偏离；但对于可测输出变量T，控制器A的控制效果更佳——超调量更小，且相比控制器B只需要约1/4的时间就能使变量重新跟踪到设定值上来。导致这种差异的原因在于控制器A准确地估计和建模了系统的干扰信号。

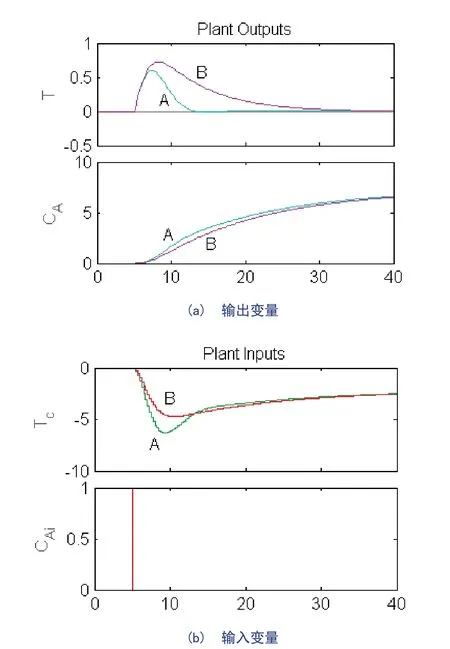
图5 不同干扰建模与估计下的仿真结果

3 结语

本文介绍了模型预测控制算法的基本理论，以Matlab软件的模型预测控制工具箱和连续搅拌釜式反应器为基础讨论了该算法的仿真方法和算法性能。从仿真结果可以看到，为了提升算法控制性能，必须注意以下几点：

（1）需要根据输入变量与输出变量的个数关系，合理设置输入变量权重、输出变量权重使得输入、输出变量有选择性的实现设定值跟踪，同时通过输入变量变化率权重控制控制增量的大小；

（2）根据实际被控对象或被控过程的物理属性合理设置输入、输出变量约束；

（3）对被控对象受到的干扰与噪声进行估计和建模，可以使控制器更符合实际工况，提高控制性能。