基于组合域的图像标签噪声预处理方法
王静红,韩德林,陈洋洋
(1.河北师范大学 计算机与网络空间安全学院,河北 石家庄 050024;2. 伊利诺伊大学厄巴纳-香槟分校 信息科学学院,伊利诺伊 厄巴纳 61801)
受益于大量已标注的干净数据集,在不同的领域[1,2]中,基于数据驱动的神经网络已具有媲美人类的分类能力。当数据集包含标签噪声时,严重影响模型准确率。标签噪声也曾诱发数据对抗性中毒[3]。因此,进行模型训练前,有必要对数据集进行标签噪声评估并修改错误标签[4]。
如图1所示,在特征空间中,多个标签对应特征之间互相纠缠,导致最终分类结果出现偏差。彻底解决特征纠缠需要依靠神经网络进行特征解耦,分类函数可以缓解特征纠缠。神经网络常使用Softmax和Sigmoid作为分类函数。Sigmoid函数对每个多标签图像做N次判断,其中N为类别数量,隐式的通过对关键特征进行组合匹配,使得在多标签图像分类中的效果优于Softmax函数。但是,Sigmoid函数具有计算成本过高、需要大量高质量的标注数据、网络训练困难等缺点。在现实任务中,需要一种快速且便利的线性组合方法,降低特征纠缠对分类结果的干扰。
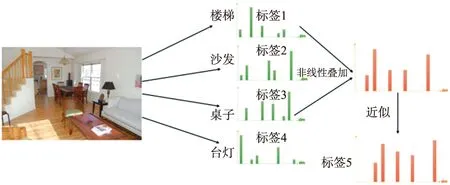
图1 多标签图像的标签纠缠
多标签分类和多分类问题的主要区别在于,多标签将造成输出空间呈现指数级增长。一阶算法的标签之间相互独立,无需考虑标签间相关性,直接将多标签问题分解为多个单标签子问题,为每个标签构建二分类器[5]。高阶算法假定标签具有相关性。文献[6]提出了包含标签信息的最小二乘多标签特征选择算法,并证明这一算法的收敛性。文献[7]通过变精度邻域粗糙集的多标签特征选择方法实现集成特征子空间,使分类特征更具泛化性。文献[8]提出一种通过使用全局和局部流形正则化,探索标签相关性的监督特征选择方法。文献[9]假设多标签数据具有共享子空间,使用半监督学习进行多标签特征选择。文献[10]更进一步,通过自适应全局结构学习使特征保留全局信息,通过流形学习增强局部结构和潜在的标签相关性,最后将两者有机地结合,使特征选择达到更好的效果。文献[11]扩展到多视图学习领域,在增强视图间的一致性和多样性时,通过更好地捕获多视图间的高阶关系,增强多标签分类性能。相比于上述效果好但耗时长的神经网络或方法,大家期望使用更加快速的预处理方法,应对多标签图像分类受到标签噪声干扰的挑战。
应对标签噪声问题,存在基于噪声模型和无噪声模型两种方法。在基于噪声模型的方法中,文献[12]提出循环调整学习率,使网络状态在欠拟合和过拟合之间变化。其假设标签噪声样本的损失较大,则调整学习率会抑制噪声样本。但是,这个假设可能会失效,把复杂的干净样本也排除在外。在基于无噪声模型的方法中,文献[13]提出某些非凸损失函数,如0-1损失,比常用的凸损失具备更强的噪声容忍度。文献[14]提出基于信息损失,给定标签和预测值之间的互信息可以被损失函数评估,但是当噪声样本数量过大时,效果不佳。
为了复用已训练完毕的神经网络参数,迁移学习应运而生。文献[15]使用自注意力机制搭建神经网络,在多个任务和多个数据集上皆取得了优异的效果。迁移学习可分为两种情况:当预训练样本足够多时,源域趋近于各个目标标签域族的期望,仅需有限样本的微调就能适应目标域;当预训练样本数量相比于目标域数据集数量不足时,需要通过领域自适应将源域与目标域对齐[16]。相对于第二种情况,第一种情况的源域和目标域差距并不显著。大家期望的是,大规模、准确且类别公平的源域数据集模型迁移到目标域数据集,例如ImageNet数据集就满足源域数据集要求。
本文的主要贡献包括3个方面:
(1)提出模块化的通用型多标签图像多分类模型(Multi-label image multi-classification model,MIMM)预处理方法,并证明源域线性组合映射至目标域的迁移误差上界。
(2)模块内,提出最大关键特征(Maximum key feature,MKF)分类函数和关键秩匹配分解(Key rank matching decomposition,KRMD)算法,缓和非独立同分布数据集引发特征纠缠的矛盾,在多标签图像分类实验中,取得准确率与运行效率的最佳平衡。
(3)引入干净的第三方数据,采取随机组合数据增广方式,通过标签数量公平性和标签噪声实验,证明MIMM方法具备自动发现标签噪声的能力。
1 图像标签噪声辨识模型
1.1 模型架构
MIMM预处理方法的全局架构如图2所示,主要包含3个模块:图像特征提取模块、微调模块以及匹配模块,单标签图像和多标签图像分别对应图中的“(1)”和“(2)”。首先,图像特征提取模块主要使用预训练参数,如已在ImageNet数据集训练的模型参数,使用其参数作为图像特征的提取器,对应于图中步骤①。其次,微调模块旨在使图像特征提取模块的单标签源域适应目标域数据,这一阶段仍使用Softmax函数抑制次要特征,对应于图中步骤②。然后,测试阶段将不同测试集,包括单标签图像和多标签图像,输入至特征提取器,将提取得到的特征使用MKF函数运算,对应于图中步骤③。最后,图像匹配模块将标准集经MKF函数得到的集合与测试集经MKF函数得到的集合,通过Match匹配模块,即KRMD算法,得到关键秩匹配最优的类别输出作为最终输出,对应于图中步骤④。

图2 MIMM方法架构
1.2 图像分类与域迁移
图像特征提取模块,使用ResNet[17]网络。当训练集只有少量样本时,采取将M-ways N-shot的数据作为标准集,与训练集类似。在此基础上添加常见的背景样本,例如草地、桌子、天空、道路、沙滩等,作为图像背景辅助信息,帮助标准集样本和测试集样本排除背景信息的干扰。在实验中,MIMM方法第一步,使用ResNet网络在ImageNet上预训练参数作为图像特征提取器。若多标签测试集含有N个类别,N<1000(1 000为ImageNet的类别数量),则有足够的特征空间进行分类。训练阶段使用标准集,模型将提取丰富的底层信息,更好地适应不同域分布。
上述方案应用于迁移学习,模型使用预训练参数,针对目标任务采取微调的策略,在源域与目标域关联程度高,即有大量重复类别的前提下,使用大量样本与少量修正样本将源域映射至目标域。MIMM方法不仅要实现单标签图像之间域迁移,还要实现多标签图像到单标签图像的组合域迁移。因此需要考虑从图像到组合图像,也即是单标签到线性组合多标签的误差。多标签图像相互纠缠导致分类结果受到干扰的定义如下所示。
定义1假设存在误差序列E,i,j∈L为标签集合,D′T为目标域集合,σ为分布交集的膨胀系数算子。
(1)当多标签分布标签变量X完全独立时
(3)
则E=0,多标签迁移误差上界问题转为多分类迁移误差上界问题的线性叠加。
(2)当多标签分布标签变量存在部分纠缠时,假设infE→0,则分布迁移后与真实分布在每个标签分布的误差趋近于0,则
(4)
式中:k为常数。膨胀系数σ导致真实混合分布与预测混合分布相差常数级。
(3)当多标签分布标签变量存在严重纠缠时,假设E→+∞,分布相交区域的非线性增长与真实相交区域的非线性增长相差极大,误差上界趋于无穷,概率趋近于0
由于神经网络的限制,导致误差上界近似于神经网络随机参数得到的标签预测结果。
定理1设η为从单标签图像分布到组合多标签图像分布的损失,σ为分布交集的膨胀系数算子,E为误差序列,L是全体标签集合。其余符号与文献[18]中定义一致,d表示分布距离,R是X→Z的固定表示函数,H是二值函数,对每个h∈H,单标签图像分类迁移至多标签图像分类的误差上界为
(6)
式中:
h′=arg minh∈H[εs(h)+εT(h)]
λs=εs(h′),λT=εT(h′),λ=λs+λT
证明通过文献[18]关于泛化误差的证明可得
(7)
将各个标签分布叠加,则
(8)
各个标签分布排除域相交损失η,则
(9)
由定义可知,源域无相交损失,则
(10)
最后,将η置于不等式右侧
非线性函数可使用算子σ近似。算子σ与误差序列E未知,若知道近似的E,就可近似的求出σ。为满足定义1中的3种情况,定义当φ不存在时,σ(φ)=0。
实验中,先使用标准集微调模型参数,再将标准集输入到模型中,与测试集一起使用MKF函数与KRMD算法进行处理。
2 图像标签噪声辨识方法
2.1 有序秩的特征选择
神经网络对图像进行特征提取,将缠绕着的特征通过映射到低维空间,解耦特征间的复杂关系,最后稀疏化语义层得到线性可分的结果。过度的稀疏化类似于硬注意力机制,只关注重要的语义,忽视对最终分类结果贡献少的信息。ReLU是在AlexNet中提出的激活函数,很长一段时间作为卷积神经网络的默认激活函数。其在众多领域都表现优秀,数学表示为ReLU=max(0,x)。ReLU通过抑制大量无用信息并侧重于关键信息使得网络稀疏,模型便能更好地进行学习。
定义2单调序数数据定义:设D是含有维度信息dimk∈K,具有k个序数属性值Ai,…,Ak,并按照从大到小排列的数据集。其中,K定义为神经网络分类模型中最后一层神经元的数量;Ai→表示按照序数排序小于Ai的下一个数值。可以表示为:D={Ai≻Aj⟺Ai>Aj,Ai→=Aj(i,j∈K)}。
定义函数MKF
MKF=max(0AZ→ →,XAZ← ←)
(11)
式中:0AZ→ →表示将数据按照维度上的数值从大到小排序后,以AZ为分界线,小于AZ值的维度将变成为0。XAZ← ←表示大于AZ值的保持原始数值。当不考虑维度与序列信息时,MKF将退化成ReLU函数。
MKF函数是一种降维函数,关注于挑选出对分类结果影响大的维度信息,这也是无法直接使用PAC等方法的原因。卷积神经网络进行图像分类时,各维度具体的数值并不重要,需要关注的是维度序列是否匹配[19]。多标签图像分类常对每个类别使用Sigmoid函数计算,准确率高,但缺点是计算量庞大且需要调节的参数复杂。作为区分数据集是否存在标签噪声而言,使用Sigmoid函数训练多标签模型就显得得不偿失了。
MKF函数的关键在于找到Z值的位置,本文有如下定义。
定义3增量幂律分布:设Aa-Ab记为ξa,其中Aa→=Ab(a,b∈K);Ab-Ac记为ξb,其中Ab→=Ac(b,c∈K)。增量之间自然有序,即当Aa>Ab>…>Ax时,ξa>ξb>…>ξx。设D′为增量的集合,则增量幂律分布可表示为D′={ξa≻ξb⟺ξa>ξb,ξa→=ξb(a,b∈K-1)}。
定义4二阶有序增量:Ai-Ad记为ξi,其中Ai→=Ad(i,d∈K);Aj-Ae记为ξj,其中Aj→=Ae(j,e∈K)。一般情况下增量之间无序,需要对增量再一次进行有序化排序。ord′={ξi≻ξj⟺ξi>ξj,ξi→=ξj(i,j∈K-1)},使得二阶增量保持从大到小有序排列。
根据定义3和定义4,Z的位置有如下可能:在对增量ξi进行由大到小排序后,(1)当增量前Z个数值AZ满足增量幂律分布,第Z+1个不满足增量幂律分布,则认为此点以后的数据不重要;(2)当增量在第Z个点ξZ出现ξZ≫ξZ→且ξZ≪ξZ←,则认为此点以后的数据不重要;(3)当增量没有出现上述两种情况,由二阶有序增量定义,对增量之间进行排序。根据数据集内所有实例的比较得到最优的位置。
上述3种情况有以下3种解决方式:

(12)
式中:为了有限次的计算,假定α的取值范围,α=(1,e]。实验时,为方便起见取值2或e,效果没有明显差异。
(2)显而易见,当某处的增量比其它处都大时,理应选择此位置。
(3)若没有出现上述两种情况,则根据数据集内所有实例的统计规律来抉择。实现二阶有序增量ord′,通过最大化每个实例的二阶增量并最小化所有实例期望与方差的下界来达到最优取值。具体表示为G
G={maxord′(ξi),ξi∈ξ} and
{{min[E(ξ)]and min[Var(ξ)]}↓}
(13)
通过以上方法能够确定Z值的位置。
2.2 关键秩匹配分解算法
小样本或非独立同分布数据微调模型参数时,不变动原分类网络模型架构,仅需做到以下两个匹配:(1)标准集与测试集的维度匹配;(2)标准集与测试集之间,重叠部分按照概率分布叠加,按秩序列分解的损失最小化匹配。


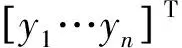
将以上问题描述为优化问题,表示为
minimizelosst=imat-(imas1+imas2)
maximumRt,Rs
s.t.β1:β2→qi:qj
3 实验
实验使用多标签数据集Pascal VOC 2007和Microsoft COCO,具体介绍如下。
Pascal VOC 2007:包含5 011个训练图像和4 952个测试图像,共20个对象类别。本文对每一个类别从网络或从原始数据集挑选10张图像,通过数据增广生成60张图像,使用训练集与验证集的留一法进行实验。
Microsoft COCO数据集由微软团队提供,针对各种视觉任务的数据集。包含12万张,总计80个类别的图像及注释。本文仍使用训练集与验证集的留一法进行实验。此数据集的图像类别更多,背景也更丰富,因此比Pascal VOC 2007更加复杂。
在多标签问题中,本文选择平均精度(Average precision,AP)作为性能的度量标准。类平均精度(Mean average precision,MAP)和类无关的平均精度(Class-agnostic average precision,APall)作为度量标准,被广泛用于多标签模型的性能评估。MAP计算所有二值分类问题平均精度的均值。AP是每个正标签的精确加权。对于每个类,计算如下
式中:m和n表示正标签和实例的数目。在本文的实验中,n是测试集的大小。Presion(i,c)是c类在第i个样本的精度。I(i,c)是指示函数,当它输出1时表示在第i个的真实标签是正确的。APall忽略每个类的注释,并将它们视为单个类。对于预测真实标签,其由m×n个值组成。这个度量标准平等的考虑每个注释,这忽视了困难的直接度量类。
以下介绍另一个度量标准宏F1
式中:查准率(Precision)用P表示,查全率(Recall)用R表示。N表示实例数量,TP表示真正例,TN表示真反例,都对应混淆矩阵的真实情况与预测结果。宏F1度量倾向于P与R都优秀的结果。
实验工具采用显卡Tesla T4和GTX 1060,使用TensorFlow 2.0实现MIMM的各个模块。预训练模块中,GPU采用Tesla T4,网络架构使用ResNet 50-v2网络进行特征提取,预训练的批大小为64,学习速率为0.001,指数学习速率每2个epoch衰减0.9,迭代5 000次。微调模块中,GPU采用GTX 1060,ResNet 50-v2作为骨干网络,损失函数仍使用交叉熵。微调的批大小为32,学习速率为0.001,指数学习速率每2个epoch衰减0.9,分别在Pascal数据集上迭代1 000次,在COCO数据集上迭代2 000次。在匹配模块中,不再使用原始分类函数,改为对标准集与测试集依次使用MKF函数和KRMD算法,得到最终的分类结果。
针对自动选择训练集,被动受到标签噪声数量影响的数据集公平性进行实验。表1中,性能度量后缀的1和2,分别代表在Pascal和COCO数据集的实验结果。
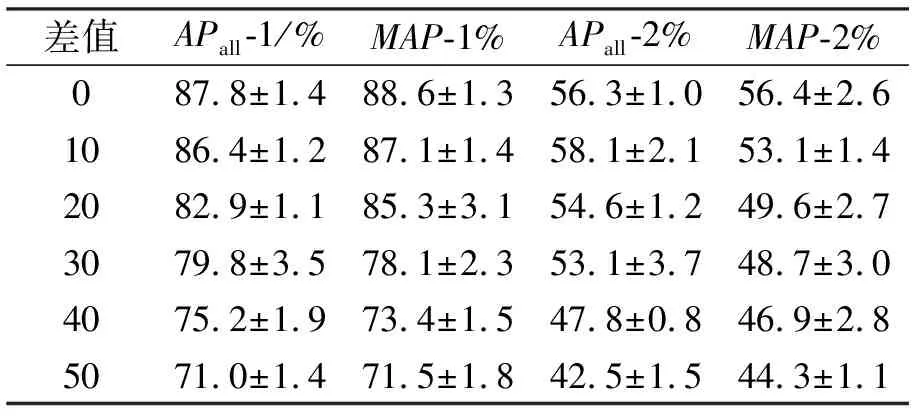
表1 标签数量对分类性能的影响
表1是随机抽取满足极端标签数量差样本做5次实验的结果。随着极端标签数量差值的增大,各个度量准则都有不同程度的下降,尤其是Pascal数据集的MAP下降17.1%。观测到在COCO数据集上,标签数量完全一致反而不如极端样本相差10,在APall度量差距为1.8%,但随着极端差值增大,各个性能度量标准逐步降低的趋势更为显著。因此,认为标签数量的公平性极大影响性能。多标签图像注释很难实现数量与质量并举,所以MIMM方法引入第三方单标签图像,相对而言可减少类别不平衡现象的出现,是更优的选择。
在表2中,对比方法是经典的多标签图像分类方法加权近似秩匹配损失(Weighted approximate-rank pairwise loss,WARP)[20]方法和卷积与循环神经网络结合(Convolutional neural networks-recurrent neural network,CNN-RNN)[21]方法,以及效果出色的指数求和对数匹配(Log-sum-exp pairwise,LSEP)[22]方法。此外,Best表示单纯使用网络,未使用本文算法得到的最佳结果。为了方便对比,将WARP1方法、CNN-RNN1方法和LSEP1方法,都使用COCO数据集训练并使用Pascal数据集进行微调,在Pascal测试集测试定义为Y迁移。WARP2方法、CNN-RNN2方法和LSEP2方法数据集训练与测试方式则与此相反。YY迁移在上述基础上,使用与测试集标签完全一致,从网络中搜集的多标签图像数据集。不同方法使用不同的分类方式。ours方法仍使用ImageNet预训练参数,在不同迁移方式下进行实验。ours分类函数表示模型使用MKF函数与KRMD算法。针对训练效率,表2中使用t表示每张图像的平均训练时间,单位是ms。受制于GPU与batch值,不同的模型训练时间有所差异。一些方法在不同数据增广方式和不同迁移方式下,计算时间相差无几,因此仅记录首个策略的运行训练时间,表中使用“如上”表示。

表2 多标签图像分类效果
首先,不考虑训练时间人为地平衡类标签训练集时,3种度量标准综合最优的是LSEP方法。在考虑训练时间时,“#3+ours+YY”在不同数据集中皆取得最优训练时间和最佳度量效果。此外,ours自动保持标签数量的公平性,训练时间均在最佳的LSEP方法基础上缩短大约10ms,证明本文的方法实现准确率和运行效率的统一。其次,任务的难度影响训练时间和准确率,不同的方法在提升准确率时,计算的代价也相应增加。
除本文方法外,其它方法的准确率与所需时间呈现正比关系。经推测由于多标签模型需要比单标签模型训练更多次,模型提取类别间最具差异的特征而忽视类别间共有特征。这需要绕过大量极值点,因此造成计算时间加长。本文方法则通过解耦特征间的纠缠,类似于从Sigmoid函数求解问题流程中采样,间接跳过许多极值点,节省训练时间。最后,当分类函数使用“ours”时,迁移方式YY在多数度量标准中优于Y(6∶1)。当分类函数使用“Sigmoid”时,迁移方式Y在多数度量标准中反而优于YY(3∶1)。这证明迁移方式YY更适合跟本文方法一起使用。除数据增广方式不同外,对比其它相关变量,#3优于#2,说明随机组合数据增广方式具有平稳性。综上所示,经过不同数据集实验,认为“#3+ours+YY”是最优的选择。
表3展示了一种处于相同分类函数,相同数据增广方式和相同迁移方式时的结果。其中,Rate表示添加的噪声占总体标签的比例,度量标准0-1表示只关注于添加的噪声是否正确匹配,而非全部标签。度量标准0-1的上缀1、2,分别表示在Pascal和COCO数据集上实验。实验展示MIMM方法针对标签噪声识别的真实效能。可以看到,当标签噪声增多时,准确率降低,并收敛于直接进行迁移图像分类的性能。因此,MIMM方法最低性能与神经网络迁移优质微调数据的性能接近。

表3 标签噪声准确率判断
4 结束语
本文为组合域标签噪声领域提供一种快速、便捷、模块化的通用型MIMM预处理方法,从理论上证明组合域的迁移误差上界,使非独立同分布的组合域数据参与模型训练,扩宽迁移学习复用同构数据的类别。在多个多标签数据集的分类任务上,MIMM预处理方法被证明在含标签噪声时,除了自动保证类别的公平性,还在多个度量标准中取得准确率与运行效率的最佳平衡效果。

