浅谈统计中平均指标在现实生活中的计算和运用分析

刘瑞

摘要：平均指标是我们日常生活中最常用的一种统计分析指标，它广泛学习、工作和生活中。本文以初一年级某小组10名学生的打字速度为例，阐述了统计工作中算术平均数、众数和中位数三种平均指标的种类和生活中的计算及运用。

关键词：平均指标 算术平均数 众数 中位数 种类 运用

一、平均指标的含义和种类

平均指标又叫平均数，它是反映社会经济现象总体在某一条件下的一般水平或者代表水平。常用平均数表示，是一种反映总体数量特征的总量指标。也是我们日常生活中最常用的一种统计分析指标，它广泛用于学习、工作和生活中，对我们认识事物，了解总体具有重要的作用。

二、平均指标的种类和计算

常用的平均指标有算数平均数、调和平均数、几何平均数、众数和中位数。其中算数平均数、众数和中位数是统计中分析总体分布趋势最常用的指标。

以下数据是某学校初一10名同学每分钟的打字测试成绩。（单位：字/分钟）

我们以初一年级某小组10名学生的打字成绩为例来阐述算数平均数、众数和中位数的计算及运用。

该组学生的打字成绩分布呈现出最小值为19字/分钟，最大值67字/分钟，成绩相差48字/分钟的特征。要进一步了解该组学生的打字速度分布情况我们可以用算数平均数、众数和中位数三种常用的平均指标进行计算分析。

（一）算数平均数的计算和运用

算数平均数又叫均值，是统计中用得最普遍的一种统计指标。算数平均数有简单算数平均数和加权算数平均数两种。

该例题中的资料为原始数据，未经分组，数值为总体各单位的标志值，所以适合采用简单算数平均数计算分析。

计算得到该组学生的平均打字速度为35.5字/分钟。

通过EXCEL表格中的统计函数AVERAGE也可以得到该组学生的平均打字速度为35.5字/分钟。

该组10名学生的打字速度参差不齐，最慢的学生19字/分钟，最快的学生达到67字/分钟，本组学生的打字速度相差48字/分钟。在了解现象总体的情况时，我们需要一个切确的数值做代表了解该组学生总体的打字速度，而算数平均数就可以把该组10名学生的打字速度平均化、抽象化和一般化。即可以用平均打字速度35.5字/分钟代表该组学生的打字成绩，我们也可以说该组10名学生的打字速度为35.5字/分钟，这样就可以了解到总体一般情况。

算数平均数是反映总体集中趋势，进行总体分布分析很重要的一个指标。它计算简单，代表性很强。同时算数平均数的反应非常灵敏，容易受到极值的影响，任何一个变量值的变化都会对平均数产生影响。

算数平均数的运用在我们的学习、工作和生活中无处不在。在学习中，学生经常需要计算自己考试成绩的平均分，了解自己的成绩水平;工作中我们的财务人员时常会计算一个单位的平均工资收入，计算到大家的平均工作时间等等;企业中常常会计算月平均销售额，月平均销量、月平均利润等来了解一个企业的运营情况;在生活中我们也时常需要了解到一个总体的平均身高、平均年龄、平均体重等。通过平均数的计算，我们既可以了解到总体分布的集中趋势，也可以对不同空间、不同地区、不同单位的同类现象进行对比研究，同时也可以对总体进行数量上的推断估计。

（二）众数（mode）的计算和运用

众数是一个现象总体中出现次数最多的标志值。它是一个位置平均数，其大小不受任何变量值的影响。特别是当一个现象总体的极端值较明显的时候，众数在平均指标中的作用尤为明显。

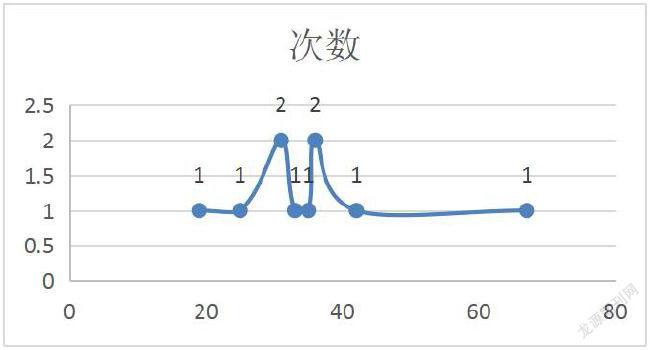
在以上案例中，该组10名学生的打字成绩出现次数最多的標志值有两个，分别是31和36，这两个变量值都出现了2次。因此我们可以判断为该组10名学生的打字成绩的众数为31和36，这里特别值得注意的是众数是一个现象总体中出现次数最多的标志值，强调的是标志值，不是出现的次数，以免把次数2当做众数来看待。

从图中我们可以看出该组10名学生的打字成绩出现了两个比较明显的集中分布趋势。

从本案例中，可以说明一组数列中众数并不是唯一不变的，一个现象总体中可以只有一个众数，也可能有两个众数、三个众数、甚至是多个众数，众数的具体个数要看其总体标志值的分布情况。

众数在我们的生活中起着非常重要的作用。平时我们在选班委的时候通常以票数最高的同学作为班长的人选，在选票中票数最多者实际上就是我们统计中的众数;通过调查发现，成年女性穿得最多的鞋子尺码为230码，230码就是成年女性鞋码的众数;在企业的销售中，销量最好的产品其实也是众数，通过众数我们可以看出消费者对产品的喜好程度，通过众数的分析可以帮助企业做生产销售方面的决策。

（三）中位数的计算和运用

中位数（median）是某组数据通过排序以后，位置排在最中间的数值。中位数的计算不受极端值的影响，通过计算中位数值可以了解标志值在总体中的位置。

中位数的计算首先要看判断数列的性质，奇数数列中位置排在最中间的只有一个数，该数则是中位数;对于偶数数列来说，位置排在中间的有两位，计算中位数的时则需取位置处于中间两位数的算数平均数。当一组数列的数字较少的情况下我们很容易找出中位数的位置，但是当数字较多的情况下我们很难一眼分辨出中位数，这个时候我们可以采用公式来确定中位数的位置，再根据位置找到对应的中位数。

以上案例中的数列为偶数数列，计算中位数的时候需要根据公式确定中位数的位置。，计算结果为5.5，则表示的是中位数处于第5位和第6位之间，对应找到第5位和第6位分别是33和35，计算得到其中位数为34。中位数34意味着该组10名学生的中间水平为打字速度34字/分钟。通过计算中位数，其他同学也可以对照中位数来比较自己在总体中的位置，大致估计到自己的排名情况。

除了中位数之外，我们还可能会用到上四分位数和下四分位数了解在总体位置分布情况，在这里不做重点讲述。生活中我们经常会说到我的工资收入处于“中等水平”，这里所说的中等水平就是指位置处于中间阶段，也就是中位数。

三、三种平均数的相互关系

平均数、众数和中位数都是分析研究总体分布的重要指标，平均数的计算考虑了所有变量值对其的影响，是分析中最重要的指标。在分析运用的时候还需要根据总体数据的具体分布情况来选择最恰当的统计指标。当总体分布出现极端值比较明显的时候，容易对平均数产生较大的影响，这时可以考虑众数和中位数来确定总体的集中趋势。总体中众数的集中程度非常明显的时候，众数又是非常不错的选择。

参考文献

[1]以核心问题引领，构建活动性课堂—“平均数”教学设计与思考[J].李月红.数学大世界（上旬）.2021（02）

[2]浅析如何让孩子行走在“发现数学”的路上—以“平均数”教学为例[J].陆敏雅.考试周刊.2021（14）

[3]探究中构建 思辨中理解—“平均数”教学设计与思考[J].周凤梅.江西教育.2021（05）

[4]巧用“横线”，深化“平均数”的认识—《平均数》一课的教学案例分析[J].白红美.好家长.2021（26）

[5]帮你分辨平均数、众数、中位数[J].范召霞.初中生辅导.2012（Z2）

[6]生活化教学模式在初中数学教学活动中的运用优势—以“平均数、中位数和众数”的教学为例新.李军课程（中）.2016，（09）