基于复数卷积-残差网络的雷达杂波幅度统计模型分类

张 良, 杨 威, 李玮杰, 杨小琪, 刘永祥

(国防科学技术大学电子科学学院, 湖南 长沙 410073)

0 引 言

自然环境的雷达回波是雷达目标检测中的杂波。对不同的杂波,雷达接收端的信号处理策略也不同[1]。杂波背景下的高精度目标检测需要对杂波幅度统计模型进行分类,再根据杂波类型采用最优的杂波抑制策略。因此,杂波幅度统计模型分类成为杂波背景下检测目标的重要步骤。

当前,杂波分类主要包括杂波属性分类和杂波幅度统计模型分类。Simon[2]首次研究了杂波属性分类问题。他将空中交通管制雷达杂波分为鸟、天气以及地杂波,在研究中提出利用分类器对提取的杂波特征进行学习实现杂波分类,取得了较高的分类准确率[2-3]。受此方法启发,众多学者在后续研究中将重点聚焦于两方面,一是杂波特征提取,二是分类器的设计和选择。在杂波特征提取方面,学者们根据杂波类型和性质提取了杂波的时域统计特征[4-5]、频域频谱特征[6-7]、图像特征[8-9]、空间方位特征[10-11]等特征。在分类器设计和选择方面,主要针对分类器的特征学习算法进行研究,通过提高特征学习精度提高杂波分类准确率,现有的分类器主要有浅层人工神经网络[2]、支持向量机[5]、反向传播(back propagation, BP)神经网络[12]等。利用分类器学习特征进行杂波属性分类的优点是可以利用少量特征实现较高的分类准确率,缺点是提取的大多是低阶特征,难以提取高阶特征,且需要人工提取特征,费时费力耗资源。

相比于对杂波属性分类研究,对杂波幅度统计模型分类的研究报道较少。杂波幅度统计模型是描述杂波幅度起伏的概率分布模型,现已提出了高斯分布、瑞利分布、韦布尔分布、对数正态分布、K分布、伽玛分布等诸多类型。杂波幅度统计模型分类是杂波背景下检测目标的重要步骤,为此学者们提出了诸多分类方法:如直方图分析法[13],该方法根据杂波的幅值统计分布拟合的直方图曲线形状进行判别,没有客观精确的判别参量,精度不高;如KS(Kolmogorov Smirnov)假设检验法[14]和归一似然比假设检验法[15],假设检验法需根据观测序列估计样本概率密度或样本累积分布函数,受样本区间划分影响大,对参数估计的精度要求高,计算复杂;如卷积神经网络分类法[16],该方法具有特征自主深度学习的特点,可直接对杂波数据进行有监督特征自学习,实现杂波分类,但由于受制于实数数据,分类效果也受限。

雷达回波数据通常是复数数据。复数数据包含实部和虚部,若将这两部分看成独立的两个通道,两个通道所包含的数据量之和就是复数数据的数据量,这是实数数据量的两倍,且复数数据包含的信息量也比实数数据更丰富,因为这两部分之间还具有相位信息,这是实数数据没有的,而不同的杂波,实部和虚部之间的相位信息也不同。利用数据特征进行分类时,数据信息越丰富,包含的特征就越多,分类精度也会越高,因此复数数据比实数数据更适用于杂波分类。Nitta[17]指出,复数数据具有更容易优化、更好的泛化特性、更快的学习效率、更好的鲁棒性等特性。Arjovsky[18]和Wisdom[19]等人的研究表明,复数具有更丰富的表征能力。但是,现有杂波幅度统计模型分类研究都是在实数数据上进行的,不仅舍弃了杂波虚部数据的信息量,还舍弃了杂波的相位信息,使数据特征的完整性和有效性遭到损坏,导致分类性能并不理想。

随着研究的不断深入,神经网络在雷达领域的应用越来越广,但复数网络的应用还较少。对复数神经网络的研究可追溯到上世纪九十年代。1990年Kim[20]将反向传播网络算法从实数域推广到复数域,同年,Clarke[21]提出了复数神经网络的算法。后来Ronny[22]给出了复数反向传播算法的一般推导,并通过PolSAR图像中不同土地类型的分类实验,验证了复数神经网络(complex-valued neural networks,CVNNs)的性能优于实数多层感知机(multilayer perceptrons,MLPs)。文献[23]介绍了从实数卷积神经网络(real-valued convolutional neural networks,RV-CNN)扩展到复数卷积神经网络(complex-valued convolutional neural network,CV-CNN)的前向传播算法和后向传播算法的推导,并通过合成孔径雷达(synthetic aperture radar, SAR)图像分类实验证明CV-CNN能获得优于RV-CNN的分类性能。文献[24]分析了常用的复数激活函数的性能,并提出了复数神经网络中复数数据的批归一化(batch normalization,BN)算法和复数权重初始化方法,并分别利用卷积神经网络(convolutional neural network，CNN)和卷积长短期记忆网络(convolutional long short-term memory,Conv-LSTM)进行SAR图像分类和自动音乐转录实验,实验结果表明复数网络的性能比实数网络的更好。但是,复数神经网络的应用也面临诸多困难,主要是因为复数在神经网络中的运算方式复杂,导致复数神经网络的功能模块构建困难[24],以池化算法实现为例,复数平均池化算法可以根据实数平均池化算法的定义直接在复数域扩展得到,但复数最大池化算法却不行。

本文引入复数神经网络,利用仿真杂波高分辨距离像(high resolution range profile,HRRP)复数数据,对雷达杂波幅度统计模型分类问题进行研究,完成了以下工作:

(1)为构建复数最大池化层,定义并改进了复数最大池化算法,通过CV-CNN对杂波幅度统计模型的分类实验,对比了两种复数最大池化算法和复数平均池化算法的分类效果,实验结果表明复数最大池化算法的分类效果更好,分类准确率为97.29%;

(2)为进一步提高分类准确率,构建了复数卷积-残差网络(complex-valued convolution-ResNet,CV-CRN),通过实验对比分析了CV-CRN采用不同池化组合的分类效果以及网络的鲁棒性,实验结果表明,CV-CRN的分类性能优于CV-CNN,且当CV-CRN中的复数卷积-池化模块和改进的复数残差块分别采用复数平均池化和正常复数最大池化时能获得更好的分类效果,分类准确率达到98.84%,且对杂噪比(杂波与噪声的功率比)为0 dB的杂波数据的分类准确率达到93.42%,具有较好的鲁棒性。

1 复数神经网络理论基础

1.1 复数运算

神经网络中的运算主要包括卷积运算和乘积运算,分别在卷积层和全连接层中完成。一维神经网络中的复数输入数据和复数权重向量分别表示为d=a+ib和W=A+iB,其中a、b、A和B都是实数向量。

卷积层中,复数权重W与复数数据d的卷积运算为

W*d=(A*a-B*b)+i(B*a+A*b)

(1)

也可用矩阵表示为

(2)

其中,R和S分别表示实部和虚部。若复数卷积层的输入数据为I∈CW1×H1×M1,该卷积层的复数权重矩阵为w∈CF×F×M1×N1,复数偏置为b∈CN1,输出数据为O∈CW2×H2×M2。复数卷积层的具体运算如下:

R(Vn)+iS(Vn)+bn

(3)

On=f(R(Vn))+if(S(Vn))

(4)

式中:Vn表示第n个神经元的复数卷积加权和;wmn表示第n个神经元与第m个通道的输入数据进行卷积的复数权重矩阵;符号*表示卷积运算;Im表示第m个通道的输入数据;f(·)表示非线性激活函数;On表示第n个神经元的输出数据。

全连接层中,复数权重W与复数数据d的乘积运算为

Wd=(Aa-Bb)+i(Ba+Ab)

(5)

用矩阵表示为

(6)

若复数全连接层的输入数据为I∈CW3×H3×M3,该卷积层的复数权重矩阵为w∈CW3×H3×M3×N2,复数偏置为b∈CN2,输出数据为O∈CW4×H4×M4。复数全连接层的具体运算如下:

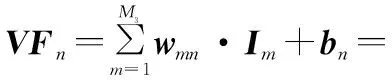
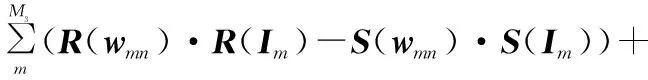
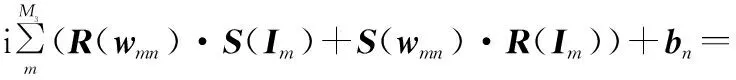
R(VFn)+iS(VFn)+bn

(7)

On=f(R(VFn))+if(S(VFn))

(8)

其中,VFn表示全连接层中第n个神经元的复数乘积加权和。

1.2 复数反向传播算法

神经网络的训练过程就是参数迭代优化的过程,而参数的迭代优化是通过误差反向传播实现的,即通过计算损失函数L对参数w的导数∂L/∂w(即误差梯度),利用优化规则w′=w-ε·(∂L/∂w)实现参数的优化,ε是学习速率。实现误差反向传播的必要条件是损失函数对网络中的变量可导,而在复数神经网络中,这个必要条件则是损失函数对网络中变量的实部和虚部都可导。

1.2.1 复数链规则

基于损失函数对网络中变量的实部和虚部都可导这一必要条件推导复数的链规则。

损失函数L对复数变量z=x+iy(x,y∈R)的误差为

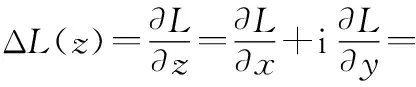
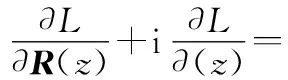
R(ΔL(z))+iS(ΔL(z))

(9)

若可由复数变量t=u+iv(u,v∈R)表示,则可得到复数链:

(10)

1.2.2 复数误差反向传播

(S(Lek[n])-S(Ok[n]))2]

(11)

其中，Ok[n]表示第k个输出神经元对第n个输入数据的预测标签。

根据复数链规则可得到权重和偏置的迭代公式:

(12)

(13)

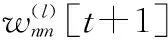
(14)

为了简化式(14),定义一个中间量“误差项”:

(15)

根据式(3)、式(4)、式(11)和式(15),式(14)可化简为

(16)

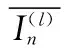
2 复数池化

在神经网络中,池化层通常接在卷积层后面,对卷积层输出的特征进行下采样,实现特征的降维压缩,这样不仅能去除冗余信息,还能降低网络复杂度、较小计算量。另外,池化层中的运算是非线性的,这也增加了网络的非线性。随着研究的深入,池化方式越来越多,平均池化和最大池化是最常用的两种。本节基于实数神经网络中的平均池化和最大池化算法的定义,基于python编程语言实现,定义了复数平均池化和复数最大池化算法,并对复数最大池化算法做了改进。

2.1 平均池化

实数神经网络中平均池化是对池域内的数据做算术平均运算,算法的定义为

(17)

式中:I表示输入特征数据;Oavg(x,y)表示在输入数据I的坐标平面内,以坐标(x,y)为起点的池域内数据的均值,k和s2分别为池的尺寸和步长,池域的大小为1≤X≤k, 1≤Y≤k。

复数神经网络处理的是包含实部和虚部的复数数据,池化运算需要同时处理复数的实部和虚部。平均池化是对池域内的数据做算术平均运算,对复数数据就是分别对实部和虚部同时做算术平均,因此可以得到复数平均池化算法的定义为

(18)

其中输入数据I∈CW3×H3×M2和输出数据为O∈CW4×H4×M2均为复数。

2.2 最大池化

实数神经网络中最大池化是对池域内的数据进行比较并提取最大值的运算,算法的定义为

(19)

式(19)筛选的最大值Omax(x,y)可看成是池域内的最显著特征,值的大小表示特征显著性的强度。

但是,对于复数而言,由于没有比较大小的准则,要定义复数最大池化算法,首先就要确定比较复数大小准则。复数包含幅度和相位信息的特质使我们可以在时域和频域对复数进行处理和分析,考虑到本文研究的是杂波幅度统计模型分类问题,所以本文考虑将复数数据转换到时域,通过比较复数幅值的大小确定最大复数。

复数最大池化算法的定义为

(20)

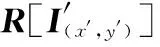
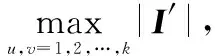
式(20)运算过程复杂繁琐,且运算量大且难以实现。为简化运算过程、减少运算量,且使其更易于实现,参考复数平均池化算法的定义,将复数最大池化算法改进为

(21)

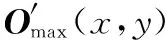
3 复数卷积-残差网络构建

本文构建了CV-CNN对上一节中定义的3种复数池化算法的分类效果进行了实验对比,实验结果表明,采用复数最大池化的分类效果更好,分类准确率为97.29%,具体见第4.2.1节。为进一步提高分类准确率,本文受文献[25]和文献[26]的启发,构建一维CV-CRN对雷达杂波幅度统计模型分类问题进行研究。CV-CRN的结构示意图如图1所示。

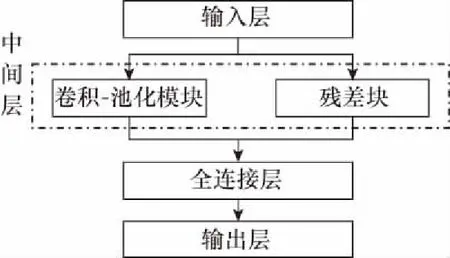
图1 CV-CRN结构示意图

输入层接收一维或多维的单通道或多通道复数数据。复数数据输入复数网络时,输入层可将复数数据作为单通道数据[23],也可将复数的实部和虚部提取成单独的通道,作为双通道数据[27]。

全连接层将卷积模块和残差模块的输出拼接,并进一步提取特征进行分类。

输出层接收最后一个全连接层输出的分类向量,在分类问题中,通常使用softmax或log_softmax输出分类标签。复数网络的输出层从全连接层接收的分类向量是复数,在执行softmax操作前需根据设置的标签的形式对其采取相应的处理方式。文献[23]设置的是实数标签,在执行softmax操作前先对复数分类向量进行取模处理;文献[24]设置的是复数标签,处理方式是分别对实部和虚部执行softmax操作,然后求平方根。本文设置的是实数标签,采取与文献[23]相同的处理方式。

3.1 复数卷积-池化模块

CNN是深度学习神经网络代表结构之一,目前已广泛应用于图片识别分类、图像分割和自然语言处理等领域,具有稀疏交互、参数共享、等变表示的特性[28],能够分层学习数据特征。

本文构建的复数卷积-池化模块如图2所示。第一个卷积层使用尺寸为5的卷积核,因为大尺寸卷积核具有更大的视野,可以提取数据较大视野的整体特征[29]。其余卷积层的卷积核尺寸为3,步长为1。Zeiler等人的研究[30]表明,使用小尺寸卷积核和步长1进行卷积能获得更好的性能。结合小尺寸卷积核的卷积层和池化层,网络能更充分的提取数据特征。因此,复数卷积-池化模块使用大尺寸卷积核与小尺寸卷积核的卷积层组合,以增强对数据特征尺度的适应性。

图2 复数卷积-池化模块结构示意图

3.2 改进的复数残差块

残差网络[25](residual network,ResNet)由一系列残差块组成,残差块的结构如图3所示。残差块包含两个以上的卷积层,其数据流向有两条,一条经过卷积层,另一条不经过卷积层。残差块的结构使能够在提升网络深度的同时,保证网络不会发生梯度消失或梯度爆炸现象,而网络深度的增加能够提取数据更深层次的特征,这种特征具有更好的鲁棒性。

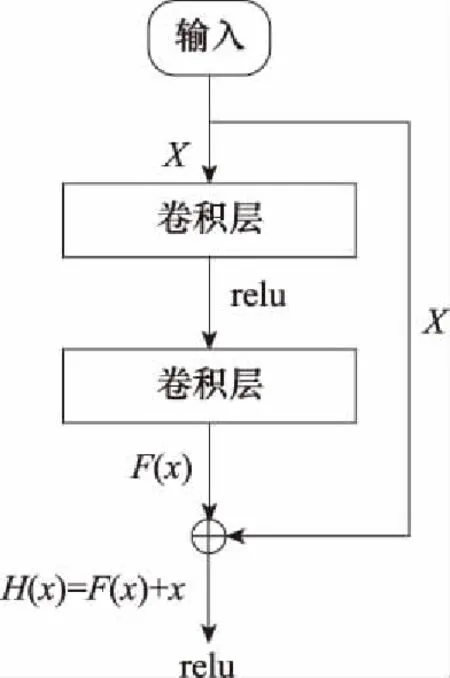
图3 残差块结构示意图

基于残差块的优点,本文考虑将残差块结构与CV-CNN结合,以构建新的复数神经网络。考虑到本文采用的杂波HRRP复数数据是一维数据,而复数卷积层输出的是二维数据,要使复数残差块得到输出H(x)=F(x)+x,就需要对特征数据F(x)降维,并将其尺寸变换成输入数据x的尺寸,因此本文对残差块结构进行了改进,构建了如图4所示的复数残差块。

图4 改进的残差块结构示意图

改进的复数残差块包含5个复数卷积层、3个复数池化层和1个尺寸变换层。数据输入后,复数卷积层对数据进行特征提取,复数池化层对数据进行特征提取并降维,尺寸变换层对数据进行尺寸变换,得到与输入数据尺寸一致的特征数据,将其与输入数据相加得到复数残差块的输出。

3.3 复数卷积-残差网络

GoogLeNet团队提出了inception结构[26],通过此结构搭建了具有稀疏性和高计算性能的神经网络。受inception结构的启发,本文将复数卷积-池化模块和改进的复数残差模块并联,构建了如图5所示的CV-CRN。复数卷积模块使用尺寸为5和3的卷积核,可以增加网络对数据特征尺度的适应性,能够更充分提取数据特征。与复数残差模块并联,可以增加网络宽度和稀疏性,提高网络计算性能,并能更好的学习数据特征。

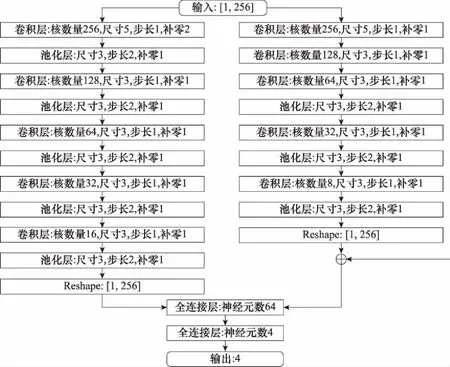
图5 CV-CRN结构示意图

在神经网络中,激活函数的作用是对卷积层、全连接层等的输出做非线性运算,给神经网络加入一些非线性因素,防止多层神经网络退化为一个多层的线性回归模型,使神经网络可以更好地解决较为复杂的问题。文献[24]对modReLU、复数ReLU(或ReLU)和zReLU这3种复数激活函数进行了分析和对比,得出的结论是:复数ReLU的性能优于modReLU和zReLU。因此,本文采用复数ReLU(或ReLU)作为CV-CRN的激活函数。3种复数激活函数的定义如下:

(1)modReLU

modReLU=ReLU(|z|+b)eiθz=

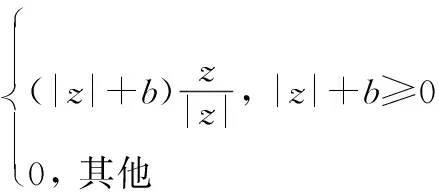
(22)

其中z∈C;θz是z的相位;b∈R是可学习参数。

(2)复数ReLU(CReLU)

CReLU=ReLU(R(z))+iReLU(S(z))

(23)

复数ReLU的本质是在数据的实部和虚部上单独使用ReLU进行激活。

(3)zReLU

(24)

其中z∈C,θz是z的相位。

另外,由于杂波幅度统计模型是概率分布模型,而交叉熵是度量两个概率分布之间差异性的重要指标,因此在网络训练阶段,本文采用交叉熵作为CV-CRN的损失函数。交叉熵公式为

L=-∑yilog(pi)

(25)

其中yi是第i个样本的真实类别标签,是pi网络对第i个样本预测的类别标签。

4 实验与分析

4.1 实验数据

需要说明的是,自然环境雷达回波的幅度统计概率分布受环境类型、环境当前气候条件等因素的影响而变化不定,不同环境类型的雷达回波可能服从不同的分布,也可能服从相同的分布,而在不同的天候条件下同一环境的雷达回波可能服从不同的分布,这导致服从不同分布的自然环境雷达回波实测数据采集非常困难。

另一方面,类似于沙地、草地等自然环境的属性标签,瑞利分布、K分布等是杂波幅度模型的类型标签。杂波幅度统计模型研究需要用精确标注的数据对分类方法进行验证,由于没有精确的标注方法,因此对实测数据标注非常困难。综上两个方面的原因,本文实验主要基于仿真数据进行。

本文利用Matlab仿真雷达杂波复数HRRP数据。目前,产生具有一定概率分布的相干随机序列有两种典型方法:零记忆非线性变换(zero memory non-linearity,ZMNL)法和球不变随机过程(spherically lnvariant random process,SIRP)法。本文参考文献[31]和文献[32]中的方法仿真相干瑞利分布、相干韦布尔分布、相干对数正态分布和相干K分布4类杂波数据,仿真原理框图如图6所示。四类杂波的概率密度函数(probability density function,PDF)和实验数据获取流程如表1和表2所示,杂波仿真数据的相位统一为均匀分布随机值。

表1 4类杂波的概率密度函数

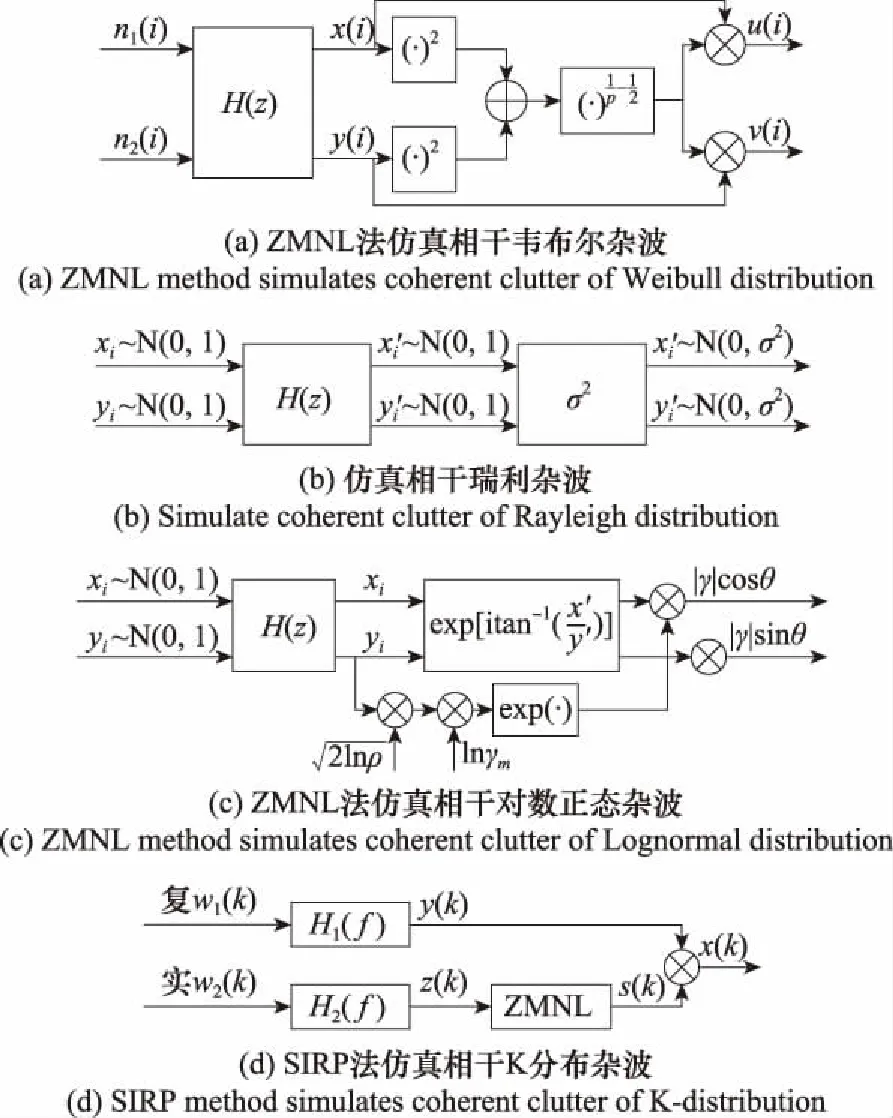
图6 雷达杂波复数HRRP仿真原理框图

杂波数据集获取流程为：

步骤 1利用SIRP法根据表2中的参数仿真得到4类无噪声杂波数据集A；

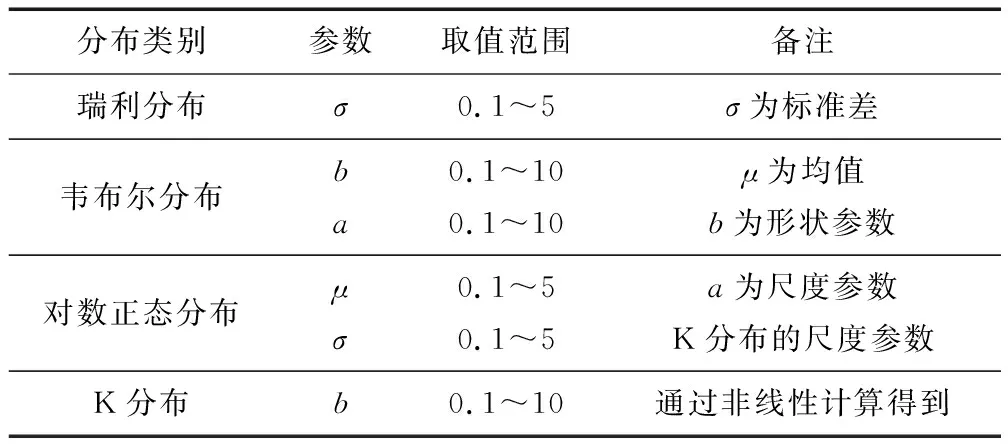
表2 仿真参数

步骤 2分别瑞利分布、韦布尔分布、对数正态分布和K分布杂波的标签设置为0、1、2和3，并与数据集A对应拼接，得到带标签数据集A′；

步骤 3给数据集A′分别添加杂噪比为0 dB、5 dB和10 dB的噪声模拟雷达电器件热噪声，得到数据集B0、B5和B10；

步骤 4将数据集A′、B0、B5和B10按5∶1的比例划分为训练数据集和测试数据集。

训练数据集每类分布10 000个样本，测试数据集每类2 000个样本，每个样本包含256个距离单元的复数数据点，并对4类数据标注实数标签。加噪声的数据集用于检验CV-CRN的鲁棒性。对上述无噪和加噪数据取模得到对应的实数HRRP数据，用于实数卷积神经网络分类对比实验。4类分布数据及其概率分布曲线随参数变化情况如图7和图8所示。

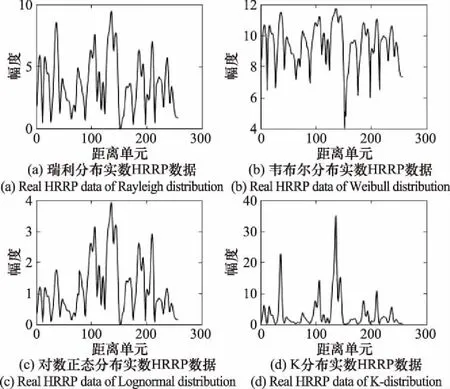
图7 4类分布取模后的实数HRRP数据图

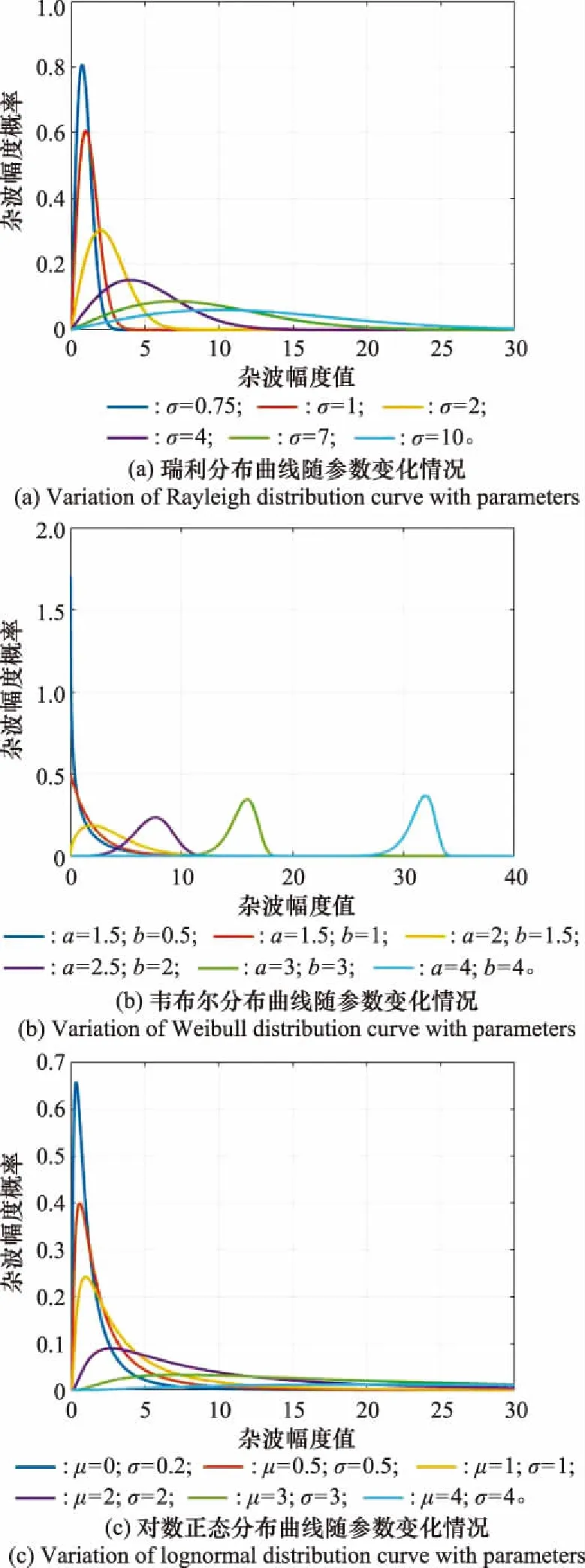
图8 4类分布曲线随参数变化情况

4.2 实验设置与结果分析

实验流程为：

步骤 1构建神经网络RV-CNN、CV-CNN和CV-CRN；

步骤 2设置网络超参数，包括小批量训练样本集batchsize、学习速率lr和网络训练次数epoch；

步骤 3这只网络训练参数优化器；

步骤 4设置分类器；

步骤 5执行实验：实验一，池化算法分类效果对比实验，将无噪声带标签数据集A′输入神经网络RV-CNN和CV-CNN，RV-CNN分别设置平均池化算法和最大池化算法，CV-CNN分别设置复数平均池化算法、复数最大池化算法和改进的复数最大池化算法，根据实验结果对比得到分类效果最佳的实数和复数池化算法；实验二，CV-CRN杂波分类实验，将无噪声带标签数据集A′输入CV-CRN中，CV-CRN的卷积模块和残差模块都分别设置复数均池化算法、复数最大池化算法和改进的复数最大池化算法，根据实验结果对比得到分类效果最优的池化算法组合；实验三，CV-CRN鲁棒性分析实验，将有噪声带标签数据集B0、B5和B10分别输入RV-CNN、CV-CNN和CV-CRN，RV-CNN和CV-CNN均采用分类性能最优的池化算法，CV-CRN采用分类性能最优的池化算法组合，根据实验结果对比分析CV-CRN的鲁棒性。

实验平台为64位Window10系统,计算机配置为Intel(R)Core(TM)i7-8700K CPU@3.70 GHz,采用Pytorch框架GPU版本实现。训练神经网络需要提前设置网络的非更新参数,也称超参数,主要包含:小批量训练样本集batchsize,是指一次迭代训练输入网络中的样本数;学习速率learningrate(lr),是指网络可优化参数的迭代优化量;网络训练次数epoch,是指训练样本集完全训练的次数。网络超参数设置如下:batchsize为10,lr为0.000 1,epoch为100。网络训练参数优化器使用Adam算法,分类器使用log_softmax函数。

4.2.1 不同池化算法及网络的分类性能对比实验

为检验正常复数最大池化算法、改进的复数最大池化算法和复数平均池化算法对杂波幅度统计模型分类的效果,构建如图9所示CV-CNN对4类无噪声的杂波仿真HRRP复数数据进行分类实验。同时构建RV-CNN进行实验,对比实数网络和复数网络的分类性能,RV-CNN的结构与CV-CNN一致。RV-CNN分别采用平均和最大池化方式,两种网络模型分别记为RV-CNN-A和RV-CNN-M;CV-CNN分别采用复数平均池化、正常复数最大池化(式(20))和改进复数最大池化(式(21)),分别记为CV-CNN-A、CV-CNN-M1和CV-CNN-M2。实验结果如表3所示。

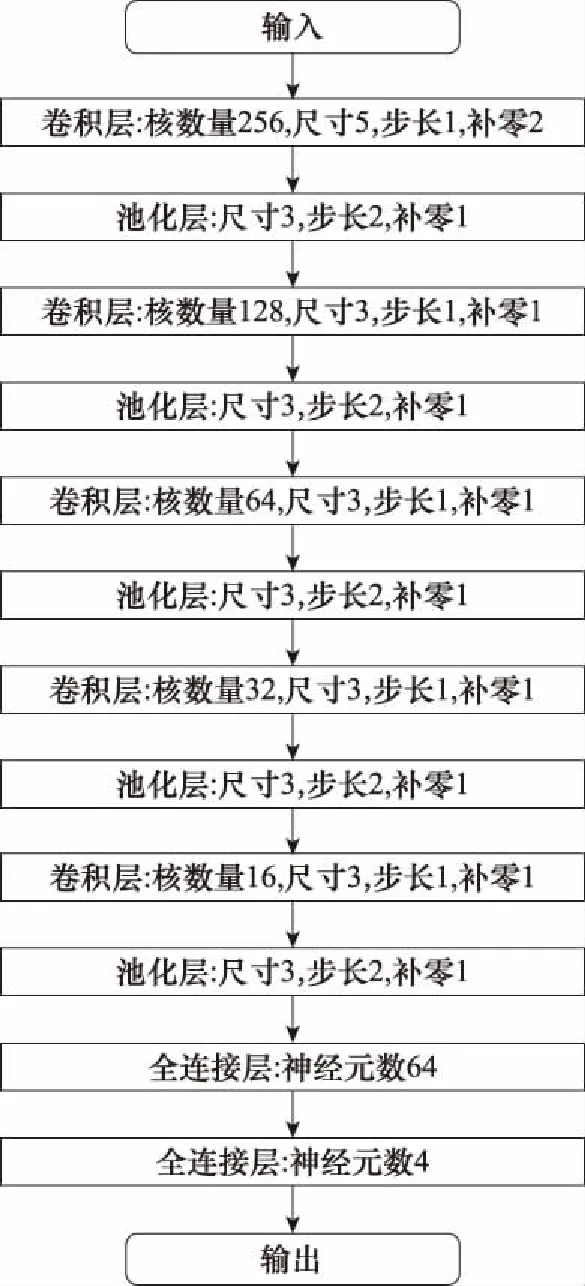
图9 CV-CNN结构示意图

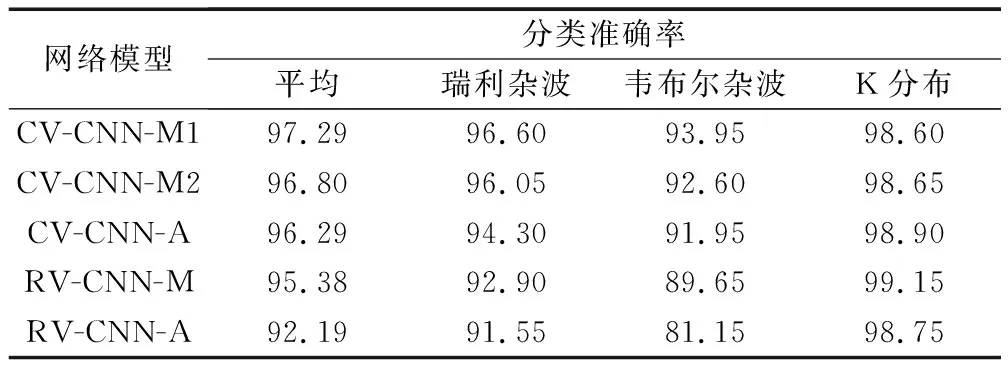
表3 卷积神经网络杂波分类实验结果

对表3中的结果对比分析可知:

(1)CV-CNN-M1和CV-CNN-M2的平均分类准确率比CV-CNN-A的平均分类准确率分别高出0.51%和1%,说明复数最大池化算法的分类效果优于复数平均池化算法;另外,RV-CNN-M的平分类准确率比RV-CNN-A的平均分类准确率高出3.19%,说明最大池化算法的分类效果优于平池化算法。原因是:平均池化算法是计算池域内特征数据的均值,得到模糊化后的特征,这会导致突出有用的特征被弱化,弱化冗余的特征被加强,使可用于分类的特征的差异性减弱;最大池化是寻找并输出池域内最突出的特征,使可用于分类的特征的差异性增强,而差异性更强的特征更有助于分类,因此分类效果会更好。

(2)CV-CNN-M2的平均分类准确率比CV-CNN-M1的平均分类准确率低0.49%,说明改进的复数最大池化算法的分类效果不如正常复数最大池化算法,但差距不大,差距主要来自于对韦布尔杂波和瑞利杂波的分类,前者的准确率比后者分别低1.35%和0.55%,说明式(21)得到的新的特征O′(x,y)是有效的分类特征,但其对这两种杂波的分类效果不如式(20)输出的最大特征O(x,y)。新特征O′(x,y)的特性及其对杂波分类的影响待下一步研究。

(3)CV-CNN-M1的平均分类准确率比RV-CNN-M的平均分类准确率高1.91%,CV-CNN-A的平均分类准确率比RV-CNN-A的平均分类准确率高4.1%,说明CV-CNN能够从复数数据中提取到更充分的特征进行分类,而CV-CNN学到了哪些有效特征用于分类待下一步研究。

4.2.2 复数卷积-残差网络杂波幅度统计模型分类实验

平均池化能够保留所有特征信息,但会导致可用于分类的特征的差异性减小,使分类准确率相对降低。最大池化是寻找并输出池域内最突出的特征,这会导致部分次重要特征被丢弃,使分类准确率受限。为充分利用两种池化算法的优势,同时降低两者的不利影响,本文以图5所示CV-CRN进行杂波幅度统计模型分类实验,探究两种池化算法的最优组合方式。CV-CRN中的复数卷积-池化模块和改进的复数残差块分别采用平均池化、正常复数最大池化和改进复数最大池化进行分类效果对比,分别记为CA、CM1、CM2和RA、RM1、RM2,形如CA-RM1表示复数卷积-池化模块采用复数平均池化、改进的复数残差块采用正常复数最大池化的组合方式,其他以此类推。分类实验结果如表4所示。

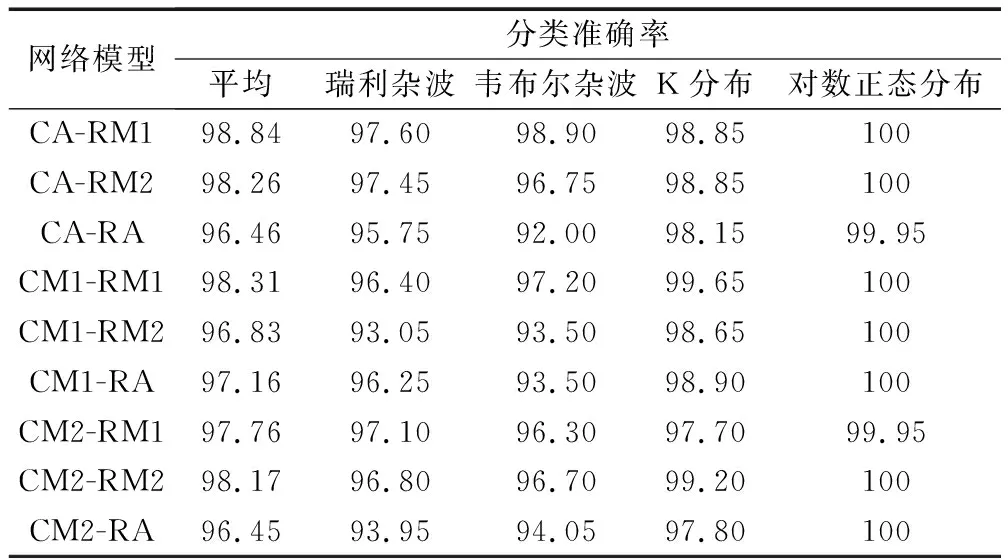
表4 复数卷积-残差网络杂波幅度统计模型分类实验结果

对表4中的结果对比分析可知:

(1)当复数卷积-池化模块采用复数平均池化算法(CA)、改进的复数残差块采用正常复数最大池化算法(RM1)时,CV-CRN获得的分类效果最好,准确率达到98.84%,说明结合使用复数卷积-池化模块学习到的模糊特征和改进的复数残差块学习到的突出特征进行分类可获得更好的分类效果。

(2)对比CM1-RM1与CA-RA的平均分类准确率可知,最大池化的分类效果优于平均池化算法,这与第4.2.1节的第(1)点分析一致。

(3)CM2-RM2的分类准确率为98.17%,这与CM1-RM1和CA-RM1的分类准确率差不大,再对比CA-RM2与CA-RM1和CM1-RM2与CM1-RM2的分类准确率可知,改进的复数最大池化算法输出的新的特征O′(x,y)是有效的分类特征,用这种特征进行杂波分类可获得较好的分类效果,但其对瑞利杂波和韦布尔杂波的分类效果比式(20)输出的最大特征O(x,y)差,这与第4.2.1节的第(2)点分析一致。

4.2.3 复数卷积-残差网络鲁棒性分析实验

本实验对添加不同杂噪比噪声的4类杂波数据进行分类,以分析CV-CRN的鲁棒性,添加CV-CNN和RV-CNN作为对比。CV-CRN采用CA-RM1的池化组合,CV-CNN采用正常复数最大池化,RV-CNN采用最大池化。实验结果如表5所示。

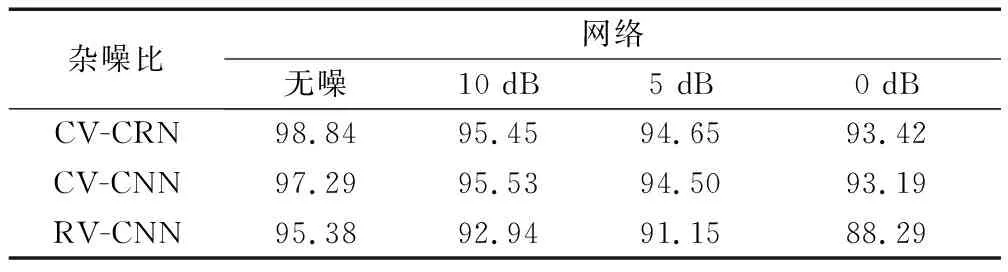
表5 复数卷积-残差网络鲁棒性分析实验结果

对表5中的结果对比分析可知:

(1)噪声对杂波分类性能的影响较大,噪声强度越大,分类效果越差;

(2)复数网络具有比实数网络更好的鲁棒性,说明复数网络抗噪能力更强;

(3)与CV-CNN相比,CV-CRN对噪声更敏感,但随着噪声增强,CV-CRN的抗噪能力比CV-CNN更强,说明CV-CRN的网络结构具有更好的鲁棒性。

5 结 论

本文引入复数神经网络,利用仿真杂波HRRP复数数据,对雷达杂波幅度统计模型分类问题进行研究,完成了以下工作:一是为构建复数最大池化层,定义并改进了复数最大池化算法,通过CV-CNN对杂波幅度统计模型的分类实验,对比了两种复数最大池化算法和复数平均池化算法的分类效果;二是为进一步提高分类准确率,构建了CV-CRN,通过实验对比分析了CV-CRN采用不同池化组合的分类效果以及网络的鲁棒性。根据实验结果得到以下结论:

(1)本文定义的复数最大池化算法和改进的复数最大池化算法都比复数平均池化算法具有更好的分类效果,且改进的复数最大池化算法输出的新特征是有效的分类特征,但其分类效果不如正常复数最大池化算法输出的特征,其合理性和物理意义还需进一步研究。

(2)复数神经网络比实数神经网络具有更好的分类效果和鲁棒性,本文构建的复数卷积-残差网络比复数卷积神经网络的分类效果和鲁棒性更好,并且当网络结合使用复数平均池化算法和复数最大池化算法时能获得更好分类性能。

另外,本文的实验结果也表明,相比于实数数据,复数数据更有利于雷达杂波幅度统计模型分类,对于复数神经网络通过利用复数数据进行训练的过程中是否利用了相位信息,以及学习到哪些特征进行分类有待进一步研究。