基于八叉树优化的MoM-PO/PTD混合算法分析目标电磁散射及辐射问题
李弘祖, 郭立新, 董春雷, 孟 肖
(西安电子科技大学物理与光电工程学院, 陕西 西安 710071)
0 引 言
在针对电大物体开展电磁散射特性的分析过程中,一般选择使用高频算法,比如物理光学(physical optics,PO)法、几何光学(geometrical optics, GO)法[1]、几何绕射理论(geometrical theory of diffraction,GTD)[2]、一致性GTD(uniform GTD,UTD)[3]、物理绕射理论(physical theory of diffraction, PTD)等。这些算法都把物体的各个部分分解出来,任一部分的散射特性跟剩余部分没有关联。所以,针对某个部分的散射场开展研究只需要考量入射波,可以不考虑剩余部分的耦合。尽管有效降低了计算难度,然而针对复杂度较高的结构计算出的结果精度不高[4]。对于低频方法,以矩量法(method of moments, MoM)[5]为例,其计算结果较为精准,但由于计算所需的时间较长以及计算机内存需求较大,一般只应用于计算电小尺寸的结构,而遇到复杂目标的电磁散射问题时,需要采用高低频混合的方式来解决。Jakobus[6]针对MoM和PO混合使用的理论进行描述,并在环境较为复杂的电磁散射中进行使用;Wang[7]将等效偶极子与迭代式MoM-PO混合算法相结合,计算了电大目标的电磁散射特性;Tong[8]成功将改进后的MoM-PO算法应用于目标和随机二维介质粗糙面的计算。
MoM的计算结果精度高,能够应用于复杂精细结构的计算。PO方法将散射源从物体本身换成了散射物体表层感应电流,随后通过电流积分计算出散射场的分布。该方法计算资源需求低、速度快,但无法精确地计算复杂结构[9-10]。因此,基于电流基的MoM和PO的混合算法[11-13]在求解电大尺寸目标散射和电大载体附近天线辐射问题中得到了广泛的应用。由于PO方法无法计算目标的棱边绕射问题,因此计算结果存在误差。鉴于此,利用PTD手段对目标区域的棱边绕射场开展计算,提高了在计算目标散射和辐射时的精准度。
此外,在计算PO区域时,传统面元遮挡判断算法的时间成本较大,因此,本文提出了基于八叉树优化的MOM-PO/PTD快速混合算法,将八叉树和后向追踪[14]算法应用于PO区域面元的遮挡判断。相较于标准射线追踪计算方法,八叉树开展优化以后的追踪手段不再选取面元作为基本单位跟剩余面元开展比较评估,所以极大地减少了计算工作量,避免了资源的浪费。最后文中将修正后的计算结果与数值方法相比较,验证了该方法的有效性,同时与未采用八叉树的混合方法相比较,结果显示本文算法使计算效率大大提升。
1 基本理论
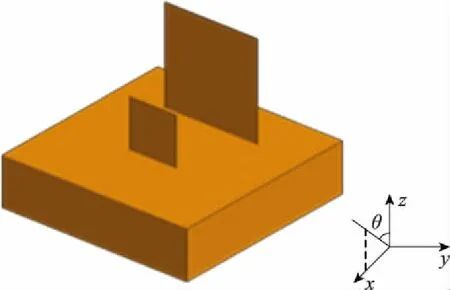
应用MoM-PO混合法[15-20]首先需要将计算模型分为两个区域[21]:MoM区域和PO区域。MoM的计算结果比较精确,一般将激励源附近、电尺寸较小、边缘和棱边较多的区域划分为MoM区,将电大尺寸平滑结构划分为PO区。如图1所示。
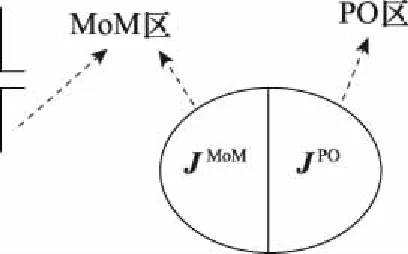
图1 MoM区域和PO区域分区
将MoM区域的电流设为JMoM,将PO区域的电流设为JPO。根据RWG基函数[22]将JMoM和JPO展开为
(1)
(2)
式中:NMoM和NPO分别为MoM区和PO区域RWG基函数数目,αn和γn分别为JMoM和JPO的展开系数。
根据高频近似条件,PO照明区的表面电流为JPO=2n×Hi,计入MoM区域产生的磁场对PO区域的影响,则电流可以表示为
(3)

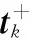
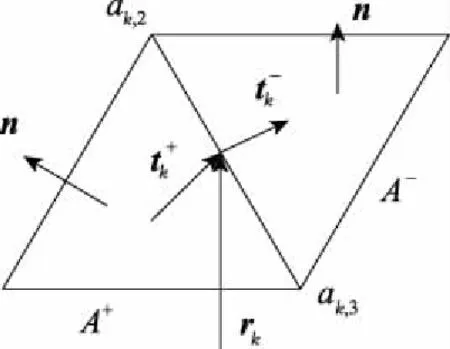
图2 在公共边上引入矢量
由RWG的性质可知,在第k条边的中点处有[11]:
(4)
(5)
其中k=1,2, …,NPO为PO区未知数的个数。将式(3)代入式(5)得
(6)
式中:
(7)
(8)
最后,在MoM区建立电场积分方程[23]:
(LEJMoM)tan+(LEJPO)tan=-Etan
(9)
将式(1)和式(2)代入式(9)得
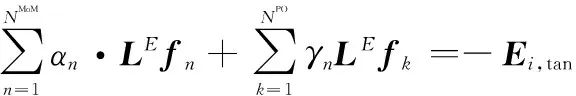
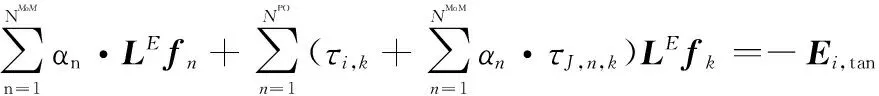


(10)
通过GalerKin法,可以得到如下线性方程组:
(ZMoM+ZMoM,PO·τk,n)·IMoM=V-ZMoM,PO·τk
(11)
其中,ZMoM=〈fm,LEfn〉,ZMoM,PO=〈fm,LEfk〉,V=〈fm,E〉。
在进行MoM位置电流的计算过程中,通过使用迭代的方式,计算得到矩量区域电流以后,将计算得到的电流系数代入公式(3)中,从而计算出PO区域的电流系数;再对电流进行积分便可得到目标的散射场和辐射场;最后,将两区域的场进行叠加,便可得到总的场强。
2 算法描述
2.1 八叉树的构造原理及应用
八叉树也被叫做八元树,是一种效率较高的空间层次树状构造,可以有效降低计算方法在空间层面上的复杂程度。八叉树的剖分均依据八分标准,可以将其看做四叉树构造进行拓展获取到的三维空间[24]。
在所需计算的空间中,八叉树剖分的过程是首先将复杂场景内所有点放在三维坐标系中,得到X,Y,Z分量上的极限大小值,以这些极限值构建一个包围整个场景的空间,并从3个方向将空间分割为大小一样的八个子空间,形成一组八叉树。针对某个包围盒开展进一步剖分的基础是这一空间内含有的三角面元数大于预设的阈值。八叉树的各个非叶节点都存在零个或八个子节点,一般把它们利用A,B,C,D,E,F,G,H进行记录。假如未能达到深度的最大值,那么开展进一步的划分[25]。
标准射线追踪方法是对所有面元一一进行明暗判定,相比于传统的射线追踪算法,经过八叉树改进后形成的射线追踪算法不再选取一个基本面元作为单位和其他面元进行明暗判定,而是先判断此包围盒所在空间中的位置,然后再判断处在该包围盒内的面片是否被遮挡。这一方法极大地减少了计算工作量,避免了资源的浪费。
该算法的步骤如下:假设一簇平行入射波方向为r=(ex,ey,ez),面元S的法向方向为n,重心坐标为P0=(x0,y0,z0),某一包围盒在XYZ方向上的最大值、最小值分别记为:Xmax、Ymax、Zmax、Xmin、Ymin、Zmin,则面元S被入射波照亮需要满足以下两个条件:
条件 1入射波方向r与面元S的法向量n应满足:rn<0;
条件 2入射波照射到面元S时没有被其他面元遮挡。
使用如下方法对条件2进行判断:从面元S的重心处发射一条射线,方向与入射射线方向相反,追踪此射线并判断其是否与其他面元相交。具体步骤如下:
设面元S上的出射射线起始位置为P0,方向为-r=(mx,my,mz)。先分析这一射线方向跟包围盒所处的位置会不会发生重叠。射线通过某个包围盒内部所满足的条件为:
(1)当mx>0时,Xmax>x0;
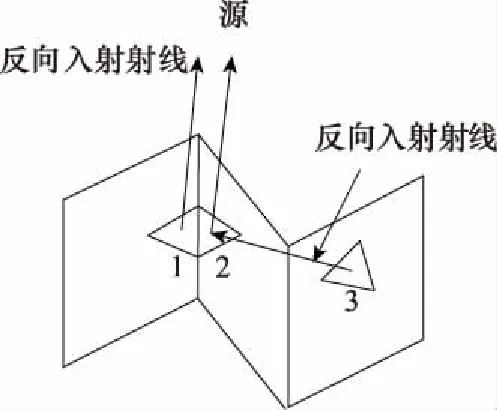
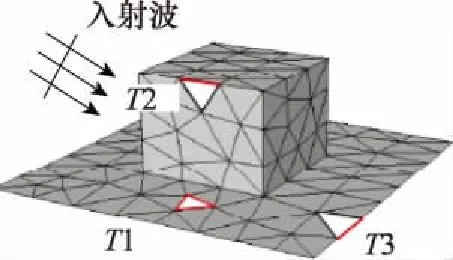
(2)当mx<0时,Xmin (3)当my>0时,Ymax>y0; (4)当my<0时,Ymin (5)当mz>0时,Zmax>z0; (6)当mz<0时,Zmin 辐射上述条件的前提下,再依据条件1分析这一射线跟包围盒中含有的面元是否会出现相交,如果存在一个面元与其相交,而且交点位置在面元当中,这说明面元m的位置在暗处,反之,其所在位置为亮处。 在射线追踪的过程中,往往会面临射线管分裂和难以判断照射区域这两问题,为解决此类问题,本文采用后向追踪方法。 和传统的射线追踪算法相比,后向追踪算法摒弃了虚拟射线管。所采用的方法是:首先,将目标模型网格划分为三角形后,记录这些三角形面片及其3个相邻面片的ID并存储在计算机内存中。其次,将每一个面元的中心作为射线的发射点,射线的方向为入射波的反方向,并沿着与此方向向源追踪。因此,判断该面元是否被照亮的条件是在进行射线追踪的过程中,此射线不被其他面元遮挡。如图3所示,编号为1和2的两个面元使用后向射线追踪算法,使得射线管分裂的问题得到有效解决。 图3 后向追踪技术示意图 在计算具有精细结构的复杂目标电磁特性时,传统的MoM-PO的混合算法通常具有很大的优势,但PO算法无法计算目标棱边的绕射场同时将阴影区电流等效为零,这与实际电流的分布情况存在差异,造成MoM-PO混合算法的计算目标散射与辐射特性时存在一定的误差。考虑到上述因素的影响,本文利用PTD[26]对PO区域的电流进行修正,在分析复杂结构目标的电磁特性问题时,将混合算法与PTD相结合,计入棱边绕射场对计算结果产生的影响,结合常用的计算模型,经过将该算法结果跟数值结果的对比,对该算法的有效性进行验证,有效拓宽了MoM-PO混合算法的应用范围。常见的劈形结构如图4所示。 图4 电磁波照射到一个典型目标上 应用PTD,得到其远区散射场计算公式为 (12) 式中:Ie和Im分别表示等效电流和等效磁流,表达式为 (13) (14) 在实际应用PTD算法的过程中,往往需要判断经三角形剖分后的目标,其三角形的各边能否构成劈形结构,如图5所示。当相邻的面元与之间处于同一个平面内并且不构成目标的棱边时,不存在棱边绕射现象;对于具有公共边的一对三角面片,当它们构成劈形结构且两面片均被照亮时,目标的棱边绕射场为总场的二分之一,但当其只有一个被照亮时,棱边绕射场可由(12)式得出。 图5 将三角形的棱边分为三类 将PO散射场和3个棱边的绕射场相叠加,便可得到修正后的PO区域总的散射场。其中,PO散射场可根据JPO求得。棱边的绕射场主要由入射电磁场以及MoM区域与PO区域的耦合电磁场所产生。入射电磁场所产生的棱边绕射场可由式(12)求得。 记耦合电磁场所产生的电磁场为EMoM,可表示为 EMoM=LE(JMoM) (15) LE(X)= (16) 将式(1)代入(16)即可求得EMoM,再将式(15)代入式(12),求解得到MoM区域与PO区域的耦合电磁场所产生的棱边绕射场。最后,将PO位置所含的三角面片计算得到的散射场开展矢量相加,结果就是总的散射场。 为了对该算法的有效性开展验证,首先对电大载体平台影响线天线方向图的情况开展分析,并跟MoM算法开展对比。 算例一为2 m×2 m×2 m的立方体前方1.75 m处有一半波对称振子天线,天线的工作频率f为1 GHz,如图6所示。计算时选择天线为MoM区,立方体为PO区。分别采用传统混合方法和改进后的计算方法计算,总的未知数目2 650。两种计算方法的运行时长和辐射方向分别通过表1和图7获取。由表1可以看出经过八叉树和后向追踪优化的算法,在判断面片的遮挡时所需时间明显减少,时间加速比为7.3。在图7中,黑线和蓝线分别表示MoM和MoM-PO/PTD方法的计算结果。由图7可以看出,MoM-PO/PTD和MoM算法吻合较好,表明经过PTD算法的修正,在210°~300°附近,天线方向图的误差明显减小,计算精度有了显著提高。 图6 天线位于立方体前 图7 位于立方体前的天线方向图 算例二为半波对称振子天线位置与5 m×2 m×2 m的简易船模型上方2 m处,天线的工作频率f为1 GHz,如图8所示。计算时选择天线为MoM区,而船为PO区。分别采用传统混合方法和改进后的计算方法计算,总的未知数目5 430。两种算法的运行时间由表1给出,时间加速比为7.7。天线的辐射方向图由图9给出,其中,黑线表示MoM计算结果,蓝线表示本文算法计算结果。可以看出,本文算法和MoM算法吻合较好,结果表明天线方向图在-30°~30°范围内的误差减小,计算精度显著提高。 图8 天线位于舰船上方 图9 位于舰船上方的天线方向图 算例三为底面尺寸2 m×2 m×0.5 m的立方体,上方为0.5 m×0.5 m和1 m×1 m的两个平板,如图10所示。计算时选择立方体上方两平板为MoM区,其余部分为PO区,总的未知数目为1 524。采用平面波照射,入射角θ=-90°~90°,φ=0°,入射波频率f=1 GHz,极化方式为HH极化。表1给出了两种算法的运行时间,时间加速比为6.5。图11给出了传统混合算法和修正后混合算法与MoM算法的单站散射场计算结果比较,其中,黑线表示MoM计算结果,蓝线表示本文算法计算结果,可以看出,本文算法和MoM算法吻合较好。 图10 底面长方体及上面两平板 表1 算法运行时间比较 图11 立方体上两平板的单站RCS结果 算例4为长为3 m的导弹模型,如图12所示。计算时选择导弹两翼和尾翼为MoM区,其余部分为PO区,总的未知数目为1 200。采用平面波照射,入射角θ=-90°~90°,φ=0°,入射波频率f=1 GHz,极化方式为HH极化。两种方法的计算时间由表1给出,时间加速比为6.2。由图13可以得出在计算较为复杂的模型时,该算法同样具有较高的精度。 图12 导弹模型 图13 导弹模型的单站RCS结果 算例5为5 m×1 m×1 m的舰船,如图14所示。计算时选择甲板上方为MoM区域,其余部分为PO区域,总未知数为7 646。采用平面波照射,入射角θ=-90~90°,φ=0°,入射波频率f=1 GHz,极化方式为HH极化。表1给出了两种算法的运行时间,时间加速比为7.5。图15给出了传统混合算法和修正后混合算法与MoM算法的单站散射场计算结果比较,其中,黑线和蓝线分别描绘的是利用MoM算法和本文算法得到的结果,能够发现,本文算法跟MoM算法具有很好的吻合度,从而对本文算法的有效性进行了验证。 图14 舰船模型 图15 舰船模型的单站RCS结果 本文针对电大载体平台上的线天线辐射问题以及目标的电磁散射问题,提出了基于八叉树的MoM-PO/PTD快速混合算法。从文中所给的算例以及表1可以看出该算法计算所需时间大幅减少,时间加速比为6~7倍。与此同时,采用PTD算法进行修正后目标的散射以及辐射的计算精度有了明显提升。2.2 后向追踪原理及应用
2.3 利用PTD修正PO区电流
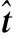
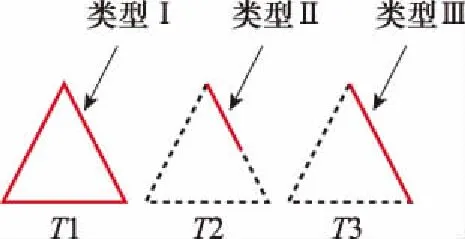
3 数值算例
3.1 MoM-PO算法计算载体上方天线方向图
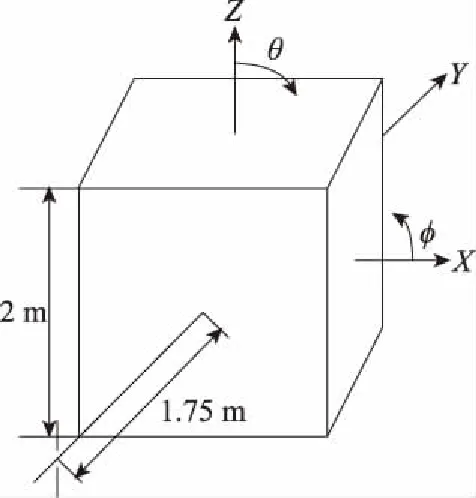
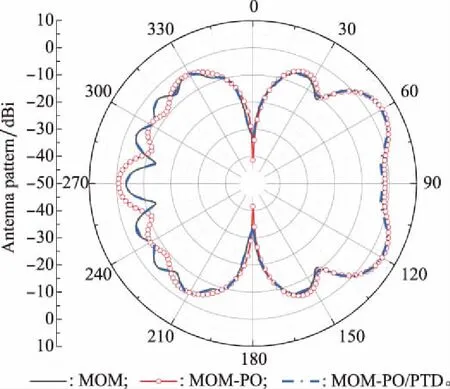
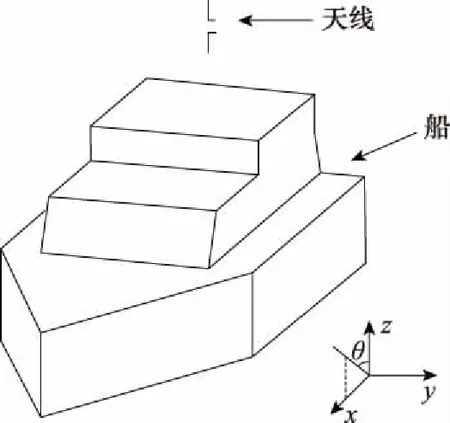
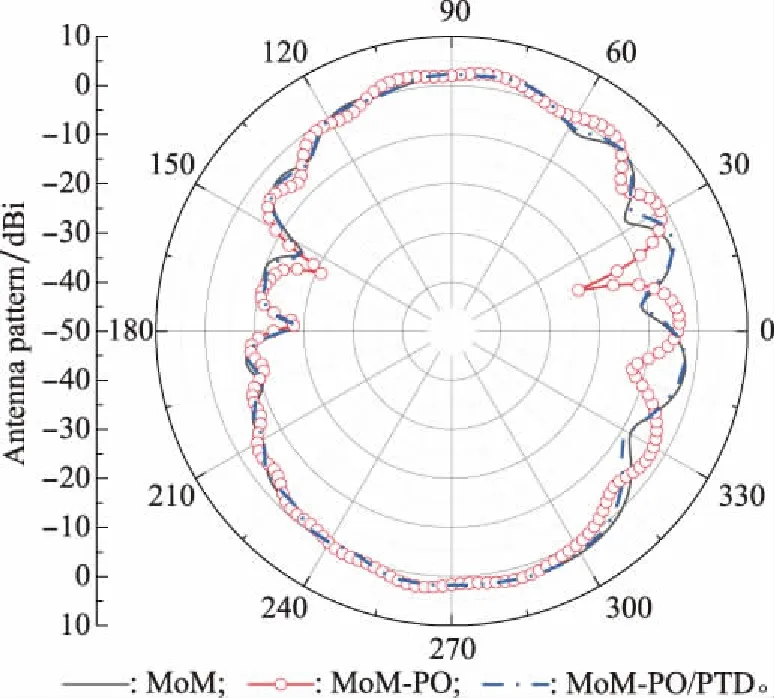
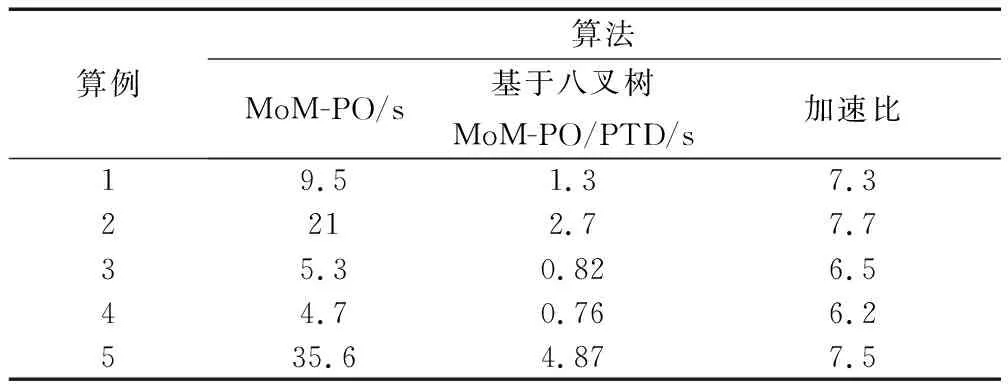
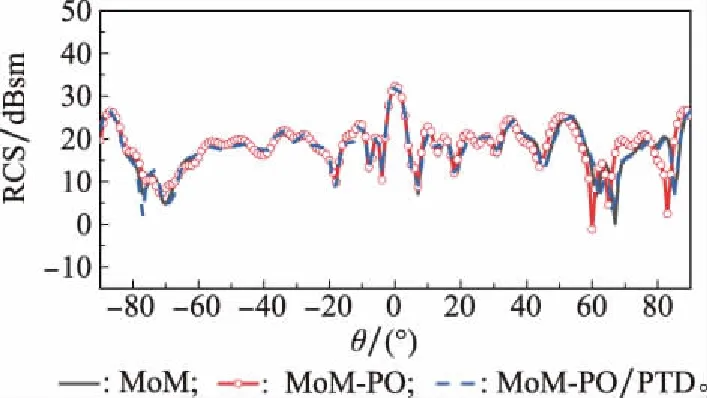
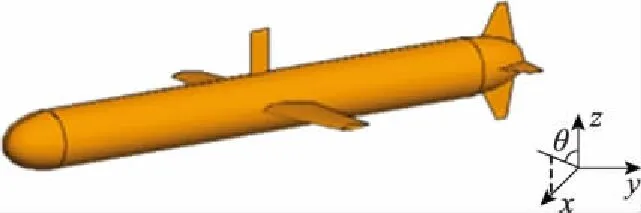
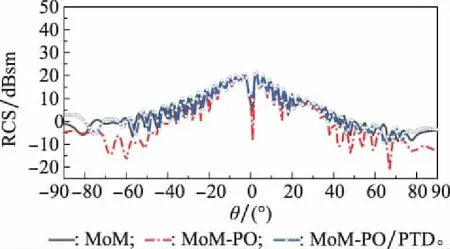
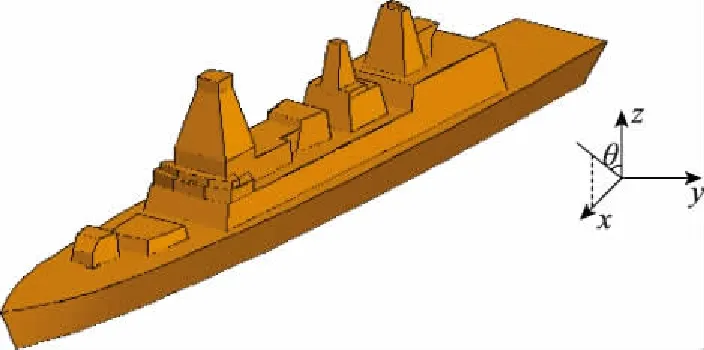
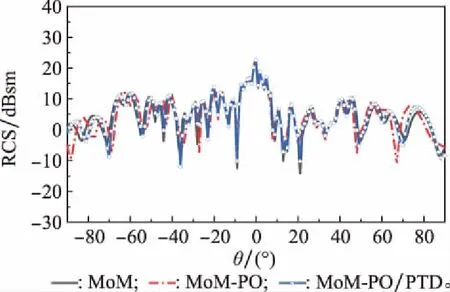
3.2 MoM-PO算法计算散射场
4 结 论

