基于KPCA和Kmeans++的遥感影像变化检测研究

冯永亮，申少格

（西安文理学院信息工程学院，陕西西安710065）

随着航空航天遥感技术的飞速发展，面对具有“三多”(多传感器、多平台、多角度)和“三高”（高空间分辨率、高光谱分辨率、高时相分辨率）的海量遥感影像数据，如何通过变化检测技术解决4W（When、Where、What object、What change）问题显得尤为迫切[1]。国内外学者陆续从不同的应用角度提出了各种各样的变化检测方法，并已广泛应用于土地利用、植被覆盖、森林变化、灾害检测等领域。但是，目前尚没有一种方法能够适合所有的应用问题。文中针对多光谱遥感影像在低维空间非线性可分这一问题，提出了一种基于KPCA 和Kmeans++的变化检测方法，求取两个时相影像差值的绝对值后，通过KPCA 将低维空间数据转为高维特征向量，进而生成差异图像，接着经过Kmeans++聚类，生成变化结果图像。

1 原理与方法

1.1 遥感影像变化检测

变化检测是通过观察不同时相的地物或现象识别其状态变化的过程[2]。变化检测过程主要分为4 个阶段：预处理阶段、变化检测阶段、阈值分割阶段以及精度评价阶段[3]。首先针对选取的数据进行数据配准和辐射校正等预处理工作，然后根据特征差异生成变化信息，接着生成具有语义特征的变化结果，最后评价变化检测的精度。国内外学者已经从数据时相、分析粒度、先验信息、空间维度、时间尺度等不同的角度对变化检测方法进行了分类[4],其中，变化检测根据分析粒度可分为像素级、特征级以及对象级3 种方式。PCA 主成分分析法就是一种基于像素级的变化检测方法。根据数据处理过程的本质，变换检测又分为有监督和无监督两类，前者需要提供适合分类的训练集，后者则将两幅图像直接进行对比，不需要提供额外的信息。而Kmeans 算法属于无监督聚类。

常用的遥感影像变化检测的方法包括差异主成分分析法、主成分差异分析法、多波段主成分分析法等。差异主成分分析法先将原始影像相减，取差值的绝对值，处理得到一个差值影像，过滤掉差值影像中的背景部分，再对差值影像进行主成分分析，得到变化结果中的第一个分量集中了两个时相影像的主要差异信息，最后进行阈值分割，得到变化图斑[5]；主成分差异分析法是先分别对不同时相的原始影像进行主成分变换，然后对两幅主成分变换后的图像取差求绝对值，作为变化信息图像。这种变换方式利用原始影像中的前几个分量对应的差值分量来作波段组合，进而反映不同时相的变化情况；多波段主成分分析法是将原始影像的各波段组合成一个两倍于原影像波段数的新影像，再对新影像进行主成分变换[6]。该文采用的是差异主成分分析法。

1.2 KPCA方法

PCA（Principal Componet Analysis）[7]即主成分分析法，利用较少的主要指标作为代表，这些主要指标彼此无关，同时尽可能多地表示原有指标的有用信息。作为多维正交变换，PCA 常被用于多光谱遥感影像处理。假设向量X=(x1,x2,…,xn)T表示原多光谱影像的像元矢量，n为波段数，将原影像X乘以线性变换矩阵A，产生新的影像Y=(y1,y2,…,yn)T，即Y=AX。变换矩阵A是多光谱影像X的协方差矩阵的特征向量的转置矩阵[8]。变化前原影像X各波段之间具有很强的相关性，经过PCA 变换后，新影像Y的各分量yi之间具有最小的相关性。PCA 有效降低了数据集的维数[9]，但它对存储空间和计算复杂度有较高的要求。对于n维空间，PCA 需形成n×n的矩阵，同时，PCA 只能处理线性数据降维，忽略了高于二阶的相互关系，提取的结果往往不是最优的。

数据在低维度空间不是线性可分的，但是在高维度空间可以变成线性可分。基于这一特征，人们引入了核主成分分析法KPCA（Kernel PCA）。KPCA是PCA 的一种扩展算法，利用非线性函数将输入空间映射到高维特征空间，并进行相关的数据处理。KPCA 的核心是将特征空间的内积运算转换为原始空间的核函数计算[10]。作为一种常用的核方法，KPCA 将原始数据通过核函数（Kernel）映射到高维度空间，再利用PCA 算法进行降维[11]。KPCA 采用了比较复杂的非线性映射，提高了非线性数据的处理效率，KPCA 方法的原理如图1所示。

图1 KPCA方法的原理

KPCA 不仅适合解决线性问题，而且能提供比PCA 更多的特征数目，可以最大限度地提取特征信息。因此，KPCA可以用于高光谱遥感影像降维处理[11]。KPCA 的推导过程如下：

1）输入空间的M个样本xk(k=1,2,…,M),xk∈RN，使，其协方差矩阵为：

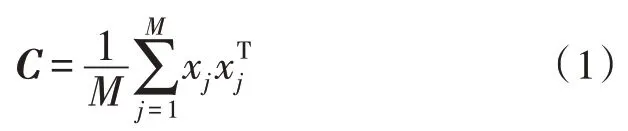
2）利用映射函数ϕ将输入空间的样本点转换为特征空间样本点：

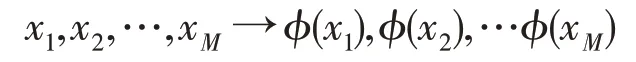
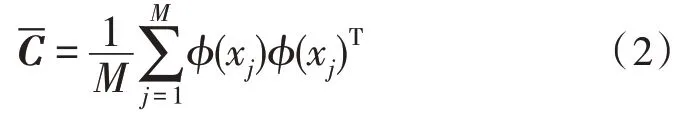
3）求解下列方程的特征值和特征向量：

4）进而求出：

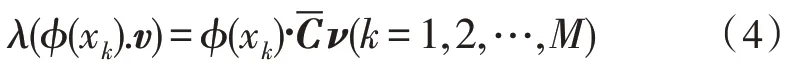
5）特征向量ν可以由ϕ(xi)(i=1,2,…,M)线性表示为：

6）由式（3）～（5）得：

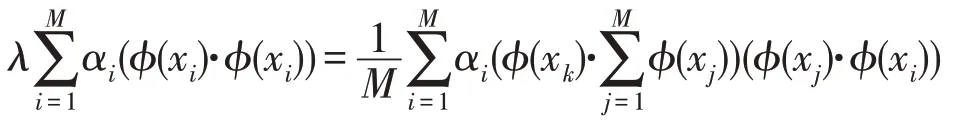
7）定义M×M矩阵K：

8）式（7）简化为：

9）显然满足Mλα=Kα，必须满足式（8）。

10）求解Mλα=Kα，即可获得要求的特征值和特征向量。

1.3 Kmeans++聚类

Kmeans++是Kmeans 的一种改进。Kmeans 是一种经典的基于划分的聚类算法，其目标是将对象集划分为若干个簇，使得簇内对象间的相似度较高，而簇间对象的相似度较低。Kmeans 首先随机选取k个初始聚类中心，接着分别计算所有点到这k个点的距离，依据距离大小将所有数据点分配到离中心点较近的簇中，再重新计算各簇的聚类中心点，根据聚类准则函数，采用迭代的方法不断重复以上过程，直到聚类中心不再变化或者是聚类准则函数收敛为止[12]。Kmeans 聚类运算简单高效，耗费资源少，且具有良好的可伸缩性，但该算法采用随机的方式选取k个初始聚类中心，不同的初始聚类中心会产生不同的聚类结果[13]。2007年，David Arthur 提出了Kmeans++[14]，该方法并不是随机地给出若干个初始聚类中心，而是先随机选取一个点作为第一个初始聚类中心，然后计算所有点到该聚类中心的距离，接着依据“聚类中心相互之间距离越远越好”的朴素原则[15]，选取新的聚类中心，不断重复，直到选出k个聚类中心，最后将这些聚类中心作为初始聚类中心来运行Kmeans。Kmeans++算法的过程如下：

Step1：随机挑选某个样本点作为第一个初始聚类中心c1，即C=c1；

Step2：分别计算每一个样本点x到其最近聚类中心的距离D(x)；

Step4：重复Step2 和Step3，直到选出了k个初始聚类中心；

Step5：利用选好的k个初始聚类中心来运行Kmeans 算法。

Kmeans++对Kmeans 算法随机选取初始聚类中心进行了改进，通过计算与距离占比相关的概率逐一选取新的初始聚类中心，直到最后选取k个初始聚类中心[16]。实践证明，该算法改进了聚类效果。

2 基于KPCA和Kmeans++的遥感影像变化检测

2.1 变化检测过程

该文采用KPCA 和Kmeans++的方法对遥感影像进行变化检测。首先对两幅不同时相的遥感影像进行预处理，求两幅影像的差值，并取绝对值，接着利用KPCA 提取特征向量形成变化差异图[17]，最后利用Kmeans++聚类算法对差异图进行分析，得到最终的变化图像。KPCA 和Kmeans++算法的流程如图2所示。

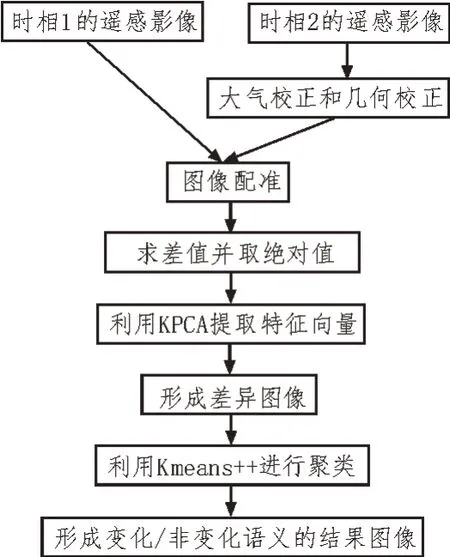
图2 KPCA和Kmeans++算法流程图

2.2 实验与分析

考虑不同数据源及传感器对变化信息的影响，该文选取2008年和2018年的Landsat8 影像作为研究对象，空间分辨率为10 m，截取其中300×300 像元，如图3所示。首先以2008年影像为基准，对2018年影像进行大气校正、几何校正，并进行图像配准；然后取两幅影像差值的绝对值，获取差异图像；接着利用KPCA 方法提取特征向量[18]，取得特征向量差异图像；最后利用Kmeans++进行聚类，获得变化/非变化语义图像，并输出变化的结果图像，如图4所示，其中白色为变化的部分，而黑色表示未变化。以目视解译的变化结果作为参考对象，计算出混淆矩阵和检测精度，总体精度较高，其值为93.5%，Kappa 系数为0.62，变化检测结果和实际结果基本一致，并且精度较高。

图3 不同时相的源图像

图4 变化检测的结果图像

3 结束语

文中提出了一种新的遥感影像变化检测方式，通过KPCA 将低维空间数据映射为高维特征向量，再通过Kmeans++聚类生成检测结果。该方法主要研究的是影像间像元数值的变化，下一步重点研究特征属性的变化。